جوليا والتحسين

حان الوقت للنظر في الحزم التي توفر طرقًا لحل مشاكل التحسين. يمكن تقليل الكثير من المشكلات لإيجاد الحد الأدنى من بعض الوظائف ، لذلك يجب أن يكون لديك حلان أو حلان في الترسانة ، وحتى حزمة كاملة.

الدخول

تواصل لغة جوليا اكتساب شعبية . في https://juliacomputing.com ، يمكنك معرفة سبب اختيار الفلكيين والروبوتات والممولين لهذه اللغة ، وفي https://academy.juliabox.com ، يمكنك بدء دورات مجانية لتعلم اللغة واستخدامها في أي نوع من أنواع التعليم الآلي. بالنسبة لأولئك الذين قرروا بدء التعلم بجدية ، أنصحك بمشاهدة الفيديو وقراءة المقالات والنقر على أجهزة الكمبيوتر المحمولة الخاصة بـ jupiter على https://julialang.org/learning/ أو على الأقل الانتقال عبر المحور من الأسفل إلى الأعلى: سيكون هناك تثبيت وميزات وتطبيق للأعمال عاجل. الآن دعونا ننكب على المكتبات.

Blackboxoxptim

BlackBoxOptim - حزمة التحسين العالمية لجوليا ( http://julialang.org/ ). يدعم كلا من مشاكل التحسين متعددة الأغراض والغرض الفردي ويركز على (meta) خوارزميات الاستدلال / الاستوكاستك (DE ، NES ، وما إلى ذلك) التي لا تتطلب أن تكون الوظيفة المحسّنة قابلة للتمييز ، على عكس الخوارزميات الحتمية التقليدية ، والتي غالبا ما تستند إلى التدرجات / التباين. كما يدعم الحوسبة المتوازية لتسريع تحسين الوظائف التي يتم تقييمها ببطء.

قم بتنزيل وتوصيل المكتبة

]add BlackBoxOptim using BlackBoxOptim 

اضبط وظيفة Rosenbrock:

 f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2 

نحن نبحث عن الحد الأدنى على الفاصل الزمني (-5 ؛ 5) لكل إحداثي لمشكلة ثنائية الأبعاد:

 res = bboptimize(f; SearchRange = (-5.0, 5.0), NumDimensions = 2) 

ماذا ستتبع الإجابة:

 Starting optimization with optimizer DiffEvoOpt{FitPopulation{Float64},RadiusLimitedSelector,BlackBoxOptim.AdaptiveDiffEvoRandBin{3},RandomBound{RangePerDimSearchSpace}} 0.00 secs, 0 evals, 0 steps Optimization stopped after 10001 steps and 0.12400007247924805 seconds Termination reason: Max number of steps (10000) reached Steps per second = 80653.17866385692 Function evals per second = 81628.98454510146 Improvements/step = 0.2087 Total function evaluations = 10122 Best candidate found: [1.0, 1.0] Fitness: 0.000000000 

والكثير من البيانات غير القابلة للقراءة ، ولكن تم العثور على الحد الأدنى. نظرًا لاستخدام stochastic ، ستكون استدعاءات الدوال أكثر قليلاً ، لذا من الأفضل استخدام اختيار الأساليب للمهام متعددة الأبعاد

 function rosenbrock(x) return( sum( 100*( x[2:end] - x[1:end-1].^2 ).^2 + ( x[1:end-1] - 1 ).^2 ) ) end res = compare_optimizers(rosenbrock; SearchRange = (-5.0, 5.0), NumDimensions = 30, MaxTime = 3.0); 

محدب

محدب هو حزمة جوليا الانضباطية برمجة محدبة (برمجة محدبة الانضباط؟). يمكن لـ Convex.jl حل البرامج الخطية ، والبرامج العددية المختلطة العددية والبرامج المحدبة المتوافقة مع DCP باستخدام مختلف الحلول ، بما في ذلك Mosek و Gurobi و ECOS و SCS و GLPK ، من خلال واجهة MathProgBase. كما يدعم التحسين مع المتغيرات المعقدة والمعاملات.

 using Pkg #      Pkg.add("Convex") Pkg.add("SCS") 

يوجد العديد من الأمثلة على الموقع: التصوير المقطعي (عملية استعادة توزيع الكثافة بواسطة تكاملات معينة على مناطق التوزيع. على سبيل المثال ، يمكنك العمل باستخدام التصوير المقطعي في صور بالأبيض والأسود) ، وتعظيم الانتروبيا ، والانحدار اللوجستي ، والبرمجة الخطية ، إلخ.

على سبيل المثال ، تحتاج إلى استيفاء الشروط:

 using Convex, SCS, LinearAlgebra x = Variable(4) p = satisfy(norm(x) <= 100, exp(x[1]) <= 5, x[2] >= 7, geomean(x[3], x[4]) >= x[2]) solve!(p, SCSSolver(verbose=0)) println(p.status) x.value 

سوف تعطي إجابة

 Optimal 4×1 Array{Float64,2}: 0.0 8.554892320716046 15.329934133156783 15.329934133156783 

القفز

JuMP هي لغة تحسين رياضية خاصة بمجال مدمج في جوليا. وهو يدعم حاليًا عددًا من الحلول المفتوحة والتجارية (Artelys Knitro و BARON و Bonmin و Cbc و Clp و Couenne و CPLEX و ECOS و FICO Xpress و GLPK و Gurobi و Ipopt و MOSEK و NLopt و SCS).

يجعل JuMP من السهل تحديد وحل مشاكل التحسين دون معرفة الخبراء ، ولكن في الوقت نفسه يسمح للخبراء بتنفيذ طرق حسابية متقدمة ، مثل استخدام البدء "hot" الفعال في البرمجة الخطية أو استخدام عمليات الاسترجاعات للتفاعل مع محللي الفروع والحدود. تعتبر JuMP سريعة أيضًا - فقد أظهرت المقاييس أن بإمكانها التعامل مع العمليات الحسابية بسرعات مماثلة للأدوات التجارية المتخصصة مثل AMPL ، مع الحفاظ على تعبير لغة برمجة عالمية عالية المستوى. يمكن دمج JuMP بسهولة في مهام سير العمل المعقدة ، بما في ذلك عمليات المحاكاة وخوادم الويب.

تتيح لك هذه الأداة التعامل مع مهام مثل:

• LP = البرمجة الخطية
• QP = البرمجة التربيعية
• SOCP = البرمجة المخروطية من الدرجة الثانية (بما في ذلك المشاكل مع القيود التربيعية المحدبة و / أو الغرض)
• MILP = برمجة خطية عدد صحيح مختلط
• البرمجة اللغوية العصبية = البرمجة غير الخطية
• MINLP = برمجة عدد صحيح غير خطية
• SDP = برمجة شبه محددة
• MISDP = برمجة عدد صحيح شبه مختلط

سيكون تحليل قدراته كافياً للعديد من المقالات ، لذلك دعنا الآن ننتقل إلى ما يلي:

Optim

Optim هناك العديد من المذيبات المتاحة من المصادر المجانية والتجارية ، والعديد منها مُلف بالفعل للاستخدام في جوليا. قليل منهم مكتوب بهذه اللغة. من حيث الأداء ، نادراً ما تكون هذه مشكلة ، حيث غالبًا ما تتم كتابتها إما في فورتران أو سي. ومع ذلك ، فإن الحلول التي تمت كتابتها مباشرة في جوليا لديها بعض المزايا.

عند كتابة برنامج (حزم) جوليا التي يحتاج الأمر إلى تحسينها ، يمكن للمبرمج إما كتابة إجراء التحسين الخاص به أو استخدام أحد الحلول المتعددة المتاحة. على سبيل المثال ، يمكن أن يكون شيء من مجموعة NLOpt. هذا يعني إضافة تبعية غير مكتوبة في جوليا ، وتحتاج إلى تقديم المزيد من الافتراضات حول البيئة التي يوجد بها المستخدم. هل لدى المستخدم مترجمين مناسبين؟ هل يمكنني استخدام كود GPL في المشروع؟

صحيح أيضًا أن استخدام محلل مكتوب في C أو Fortran يجعل من المستحيل استخدام إحدى ميزات جوليا الرئيسية: الإرسال المتعدد. نظرًا لأن Optim مكتوب بالكامل في Julia ، يمكننا حاليًا استخدام نظام إرسال لتسهيل استخدام الإعدادات المسبقة المخصصة. تتمثل الميزة المخطط لها في هذا الاتجاه في السماح باختيار يحله المستخدم من المذيبات لمراحل مختلفة من الخوارزمية ، يعتمد كليا على الإرسال بدلاً من القدرات المحددة مسبقًا التي اختارها مطورو Optim.

تعني الحزمة على Julia أيضًا أن Optim لديه حق الوصول إلى وظائف التمييز التلقائي من خلال الحزم في JuliaDiff .

دليل

تابع:

 ]add Optim using Optim #   f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2 x0 = [0.0, 0.0] optimize(f, x0) 

نحصل على إجابة بتقرير مناسب:

 Results of Optimization Algorithm * Algorithm: Nelder-Mead #   * Starting Point: [0.0,0.0] * Minimizer: [0.9999634355313174,0.9999315506115275] * Minimum: 3.525527e-09 * Iterations: 60 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 118 

ومقارنة مع بلدي نيلدر ميد!

 using BenchmarkTools @benchmark optimize(f, x0) BenchmarkTools.Trial: memory estimate: 11.00 KiB allocs estimate: 419 -------------- minimum time: 39.078 μs (0.00% GC) median time: 43.420 μs (0.00% GC) mean time: 53.024 μs (15.02% GC) maximum time: 59.992 ms (99.83% GC) -------------- samples: 10000 evals/sample: 1 

  for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end 

 ofNelderMid(fit = [0, 0.]) step= 118 7.7234e-5 f = 2.797-18 x = [1.0, 1.0] @benchmark ofNelderMid(fit = [0., 0.]) BenchmarkTools.Trial: memory estimate: 394.03 KiB allocs estimate: 6632 -------------- minimum time: 717.221 μs (0.00% GC) median time: 769.325 μs (0.00% GC) mean time: 854.644 μs (5.04% GC) maximum time: 50.429 ms (98.01% GC) -------------- samples: 5826 evals/sample: 1 

يمكنك اختيار الطريقة المستخدمة:

 optimize(f, x0, LBFGS()) Results of Optimization Algorithm * Algorithm: L-BFGS * Starting Point: [0.0,0.0] * Minimizer: [0.9999999926662504,0.9999999853325008] * Minimum: 5.378388e-17 * Iterations: 24 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 4.54e-11 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 5.30e-03 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 9.88e-14 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 67 * Gradient Calls: 67 

والحصول على وثائق مفصلة والمراجع إليها

 ?LBFGS() 

يمكنك ضبط وظائف Jacobian و Hessian

 function g!(G, x) G[1] = -2.0 * (1.0 - x[1]) - 400.0 * (x[2] - x[1]^2) * x[1] G[2] = 200.0 * (x[2] - x[1]^2) end function h!(H, x) H[1, 1] = 2.0 - 400.0 * x[2] + 1200.0 * x[1]^2 H[1, 2] = -400.0 * x[1] H[2, 1] = -400.0 * x[1] H[2, 2] = 200.0 end optimize(f, g!, h!, x0) Results of Optimization Algorithm * Algorithm: Newtons Method * Starting Point: [0.0,0.0] * Minimizer: [0.9999999999999994,0.9999999999999989] * Minimum: 3.081488e-31 * Iterations: 14 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 3.06e-09 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 3.03e+13 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 1.11e-15 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 44 * Gradient Calls: 44 * Hessian Calls: 14 

كما ترون ، قام تلقائيًا بصياغة طريقة نيوتن. وهكذا يمكنك تعيين منطقة البحث واستخدام النسب التدرج:

 lower = [1.25, -2.1] upper = [Inf, Inf] initial_x = [2.0, 2.0] inner_optimizer = GradientDescent() results = optimize(f, g!, lower, upper, initial_x, Fminbox(inner_optimizer)) Results of Optimization Algorithm * Algorithm: Fminbox with Gradient Descent * Starting Point: [2.0,2.0] * Minimizer: [1.2500000000000002,1.5625000000000004] * Minimum: 6.250000e-02 * Iterations: 8 * Convergence: true * |x - x'| ≤ 0.0e+00: true |x - x'| = 0.00e+00 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: true |f(x) - f(x')| = 0.00e+00 |f(x)| * |g(x)| ≤ 1.0e-08: false |g(x)| = 5.00e-01 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 84382 * Gradient Calls: 84382 

حسنًا ، أو لا أعرف ، دعنا نقول أنك تريد حل المعادلة

 f_univariate(x) = 2x^2+3x+1 optimize(f_univariate, -2.0, 1.0) Results of Optimization Algorithm * Algorithm: Brents Method * Search Interval: [-2.000000, 1.000000] * Minimizer: -7.500000e-01 * Minimum: -1.250000e-01 * Iterations: 7 * Convergence: max(|x - x_upper|, |x - x_lower|) <= 2*(1.5e-08*|x|+2.2e-16): true * Objective Function Calls: 8 

واختار لك طريقة برنت .
أو وجود بيانات تجريبية ، تحتاج إلى تحسين معاملات النموذج

 F(p, x) = p[1]*cos(p[2]*x) + p[2]*sin(p[1]*x) model(p) = sum( [ (F(p, xdata[i]) - ydata[i])^2 for i = 1:length(xdata)] ) xdata = [-2,-1.64,-1.33,-0.7,0,0.45,1.2,1.64,2.32,2.9] ydata = [0.699369,0.700462,0.695354,1.03905,1.97389,2.41143,1.91091,0.919576,-0.730975,-1.42001] res2 = optimize(model, [1.0, 0.2]) Results of Optimization Algorithm * Algorithm: Nelder-Mead * Starting Point: [1.0,0.2] * Minimizer: [1.8818299027162517,0.7002244825046421] * Minimum: 5.381270e-02 * Iterations: 34 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 71 

 P = Optim.minimizer(res2) Y = [ F(P, x) for x in xdata] using Plots plotly() plot(xdata, ydata) plot!(xdata, Y) 

مكافأة إنشاء وظيفة الاختبار الخاصة بك

تستخدم الفكرة من مقالة خابروف . يمكنك تكوين كل حد أدنى محلي:

 """ https://habr.com/ru/post/349660/ :param n:   :param a:    ,   ,    /      :param c:    :param p:       :param b:    :return:  ,       ,          """ function feldbaum(x; n=5, a=[3 2; 4 3; 2 1; 4 5; .5 .5], c=[-1 2; 2 1; -3 2; -2 -2; 1.5 -2], p=[9 6; 1 1; 1.5 1.4; 1.2 1.3; 0.5 0.5], b=[0 1 3.2 2 4.6]) l = zeros(n) for i = 1:n res = 0 for j = 1:size(x,1) res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end 

ويمكنك ترك كل شيء لإرادة عشوائية سبحانه وتعالى

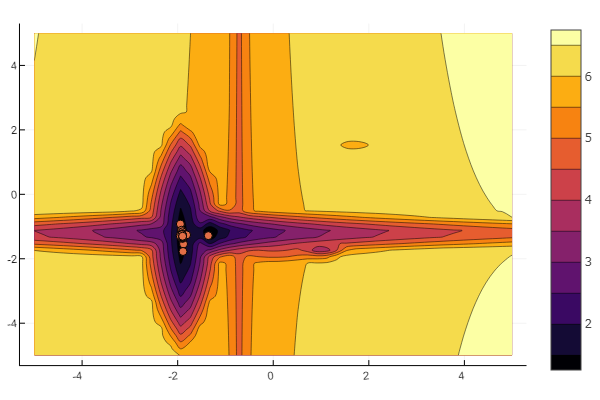
 n=10 m = 2 a = rand(0:0.1:6, n, m) c = rand(-2:0.1:2, n, m) p = rand(0:0.1:2, n, m) b = rand(0:0.1:8, n, m) function feldbaum(x) l = zeros(n) for i = 1:n res = 0 for j = 1:m res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end 

ولكن كما ترون من الصورة الافتتاحية ، فإن مجموعة من الجسيمات بمثل هذه الارتياح ليست مخيفة.

يجب أن يتم ذلك. كما ترون ، جوليا لديها بيئة رياضية قوية وحديثة إلى حد ما تسمح بإجراء دراسات رقمية معقدة دون الانحناء إلى تجريد البرمجة منخفضة المستوى. وهذه مناسبة ممتازة لمواصلة دراسة هذه اللغة.

حظا سعيدا للجميع!