تنفيذ حركة الجسيمات الحرة على ReactJS

تحية طيبة أريد أن أوضح لك إحدى الطرق التي تحقق بها حرية حركة الجزيئات في النطاق المحدد. سأستخدم ReactJS لإكمال هذه المهمة. لكن الخوارزمية نفسها ستظل عامة ، ويمكنك استخدامها في أي مكان.



في نهاية المقال ، سنقوم بإنشاء شيء من هذا القبيل معك.

طريقة خاطئة

أول ما يتبادر إلى الذهن لحل هذه المشكلة هو ببساطة العشوائية X و Y. دعونا نرى ما يحدث.


نحن هنا نحول العشوائية كل ثانية في النطاق من -50 إلى 50 في X وفي Y:

Math.random() * 100 - 50 

والانتقال سلس باستخدام خاصية انتقال css:

 transition: transform 1s linear; 

كما ترون ، النتيجة ليست ما نريده تمامًا. بالطبع ، يمكنك تهيئته بحيث تتم إضافة التحول إلى موضع موجود ، ثم سيكون أقرب إلى الحقيقة. ولكن لا يزال ، نحن بحاجة إلى الذهاب بطريقة مختلفة قليلا.

الطريق الصحيح

الطريقة السابقة تبدو ملتوية للغاية لعدة أسباب:

1. في الواقع ، لا يمكن للجسيم أن يغير اتجاهه فجأة.
2. الجسيمات لكل فترة زمنية يجب أن تمر مسافة معينة

وهذا يشير إلى أننا نحتاج إلى العشوائية بالضبط في الاتجاه الذي ستتحرك فيه الجسيمات ، وفي نطاق معين من الدرجات ، بحيث لا توجد انعطافات حادة. لذلك سوف نحل المشكلة الأولى.

ولحل المشكلة الثانية ، سنشير مقدمًا إلى الخطوة التي يجب من خلالها تحويل الجسيم خلال الفترة الزمنية.

الآن عليك أن تتذكر المسار الأساسي لعلم المثلثات. نحن نعرف طول l وزاوية deg . تحتاج إلى العثور على X و Y

الخطيئة هي نسبة الجانب الآخر إلى الوتر.
كوس هي نسبة الجانب إلى الوتر.

نحصل على الصيغ التالية لحساب:

 x = cos(deg) * l y = sin(deg) * l 

ولكن هناك شيء واحد. في Math.sin ، يأخذ Math.sin زاوية بالراديان ( قيمة من -1 إلى 1 ). لذلك ، قبل إلقاء زاوية ، يجب عليك أولاً تحويلها إلى راديان.

 deg() = deg() * Pi / 180 

نكتب وظيفة ستحصل على زاوية عند المدخلات ، والمسافة التي يحتاج الجسيم إلى إزاحتها. وستقوم الدالة { x, y } بقيمنا الخاصة بالتحول بإرجاع الوظيفة.

 function getShift(deg, step) { return { x: +(Math.cos(deg * Math.PI / 180) * step).toFixed(), y: +(Math.sin(deg * Math.PI / 180) * step).toFixed(), }; }; 

سنختبر ما ستنتجه وظيفتنا. لنفترض أننا نقل الجسيمات 10px كل مرة. دعونا نرى ما يعود getShift لزوايا مختلفة.

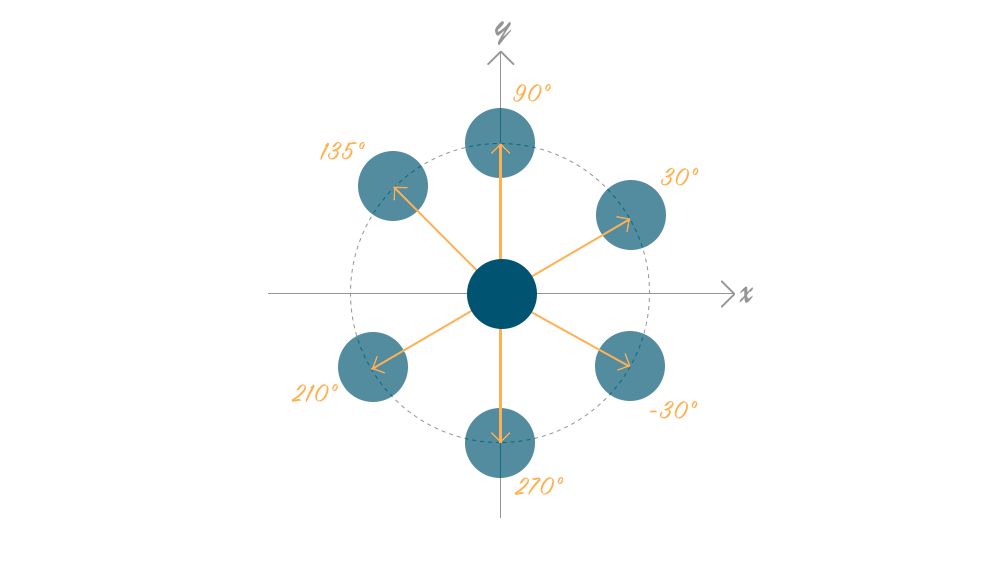
 getShift(30, 10); // {x: 9, y: 5} getShift(90, 10); // {x: 0, y: 10} getShift(135, 10); // {x: -7, y: 7} getShift(210, 10); // {x: -9, y: -5} getShift(-30, 10); // {x: 9, y: -5} 

حسنا ، على ما يبدو ، هل توافق؟

الآن حاول إصلاح تطبيقنا المكتوب الأول.


بالفعل ليست سيئة! يبقى أن ندرك الإطار الذي بعده لن يتمكن الجسيم من الطيران. منذ الآن ، وعلى الأرجح بعد مرور بعض الوقت ، ستطير الدائرة الزرقاء خارج الشاشة.

من أجل جعل الإطار ، ستحتاج إلى إضافة ثابت جديد. وإضافة أيضا شرط واحد. هذا هو المكان الذي يعمل في حين أن حلقة بالنسبة لنا. إذا كان هناك قيود على الطريق ، فسنقوم بتدوير الزاوية حتى ينتهي الدور من الإطار.

للوضوح ، أضف مربعًا أصفرًا ، لن تتمكن الدائرة بعده من الطيران. إليك ما حدث:


خوارزمية لدينا جاهزة تماما للاستخدام. الخطوة التالية هي تطبيق هذه الخوارزمية على ReactJS باستخدام قدراتها.

نقل الخوارزمية إلى ReactJS

عند نقل تطبيقنا إلى ReactJS ، سنضع أنفسنا المهام التالية:

1. قم MovingPart مجمّع MovingPart بحيث يمكنك رمي أي شيء فيه.
2. في الحالة ، سنقوم بتخزين قيمتي X و Y ، حيث إنهما ضروريان فقط لإعادة رسم المكون.
3. في الخارج ، سيتم طرح مكون في فاصل زمني ، وهو حدود لا يمكن تجاوزه بعد ذلك ، والخطوة التي سيتم بها نقل العنصر في فاصل زمني واحد.
4. دعنا نرسم القليل من MovingPart مع العديد من مكونات MovingPart ، من أجل تخيل تقريبًا أين يمكن تطبيقها في الحياة الحقيقية

نتيجة لذلك ، حصلنا على المثال التالي:


سنتخذ البيانات الأولية من مجموعة data .

بعد ذلك ، نصف مكون MovingPart :

• الفاصل الزمني (الفاصل الزمني) والمسافة (المسافة) والتحول في خطوة واحدة (الخطوة) نخرج من الدعائم ؛
• يتم تحديد الحد الأقصى للدوران أثناء الحركة (maxRotate) وزاوية التحول الحالية (deg) داخل العنصر ؛
• تؤخذ القيم x و y إلى حالة المكون ؛
• يتم تعريف طريقة getShift على أنها الطريقة الداخلية للمكون.

بعد ذلك ، باستخدام حلقة map ، MovingPart كل العناصر ، MovingPart بمكون MovingPart الذي MovingPart .

شكرا لاهتمامكم! كان هذا مقالتي الأولى عن حبري ، آمل أن يكون مفيدًا. جربه ، التجربة.