البرمجة العلائقية: الألم والفائدة والألم مرة أخرى

في المنشور السابق قلنا بالتفصيل ما نعلمه الطلاب في مجال "البرمجة الصناعية". بالنسبة لأولئك الذين تكمن اهتماماتهم في مجال نظري أكثر ، على سبيل المثال ، تنجذب إلى نماذج البرمجة الجديدة أو الرياضيات المجردة المستخدمة في البحث النظري في البرمجة ، هناك تخصص آخر - "لغات البرمجة".

سأتحدث اليوم عن بحثي في ​​مجال البرمجة العلائقية ، وهو ما أقوم به في الجامعة وكطالب باحث في مختبر أدوات اللغة JetBrains Research.

ما هي البرمجة العلائقية؟ عادة ما نقوم بتشغيل وظيفة مع الحجج والحصول على النتيجة. وفي الحالة العلائقية ، يمكنك القيام بالعكس: إصلاح النتيجة وسيطة واحدة ، والحصول على الوسيطة الثانية. الشيء الرئيسي هو كتابة التعليمات البرمجية بشكل صحيح والتحلي بالصبر والحصول على كتلة جيدة.

عن نفسي

اسمي ديمتري روزبلوخاس ، أنا طالب في السنة الأولى في جامعة سان بطرسبرج للصحة والسلامة والبيئة ، وفي العام الماضي تخرجت من برنامج البكالوريوس في الجامعة الأكاديمية في مجال "لغات البرمجة". منذ السنة الثالثة من الدراسات الجامعية ، أنا أيضًا طالب أبحاث في مختبر أدوات اللغة في JetBrains Research.

البرمجة العلائقية

حقائق عامة

البرمجة العلائقية هي عندما تصف ، بدلاً من الدوال ، العلاقة بين الوسائط والنتيجة. إذا تم توضيح اللغة لهذا ، فيمكنك الحصول على مكافآت معينة ، على سبيل المثال ، القدرة على تشغيل الوظيفة في الاتجاه المعاكس (استعادة القيم المحتملة للوسيطات كنتيجة).

بشكل عام ، يمكن القيام بذلك بأي لغة منطقية ، ولكن الاهتمام بالبرمجة العلائقية قد نشأ في وقت واحد مع ظهور minKanren بلغة منطقية نقية في أضيق الحدود منذ حوالي عشر سنوات ، مما جعل من الممكن وصف واستخدام مثل هذه العلاقات بسهولة.

فيما يلي بعض حالات الاستخدام الأكثر تقدماً: يمكنك كتابة مدقق إثبات واستخدامه للعثور على دليل ( قريب وآخرون ، 2008 ) أو إنشاء مترجم فوري لبعض اللغات واستخدامه لإنشاء برامج مجموعة برامج اختبار ( Byrd et al.، 2017 ).

بناء الجملة ومثال لعبة

miniKanren هي لغة صغيرة ، وتستخدم فقط المنشآت الرياضية الأساسية لوصف العلاقات. هذه لغة مضمّنة ، بداياتها هي مكتبة لبعض اللغات الخارجية ، ويمكن استخدام برامج miniKanren الصغيرة داخل برنامج بلغة أخرى.

لغات أجنبية مناسبة ل miniKanren ، مجموعة كاملة. في البداية ، كان هناك Scheme ، ونحن نعمل مع إصدار Ocaml ( OCanren ) ، ويمكن الاطلاع على القائمة الكاملة في minikanren.org . الأمثلة في هذه المقالة ستكون أيضًا على OCanren. تضيف العديد من التطبيقات وظائف المساعد ، لكننا سنركز فقط على اللغة الأساسية.

لنبدأ بأنواع البيانات. تقليديا ، يمكن تقسيمها إلى نوعين:

• الثوابت هي بعض البيانات من اللغة التي نحن مضمنون فيها. السلاسل والأرقام وحتى المصفوفات. لكن بالنسبة إلى miniKanren الأساسي ، كل هذا مربع أسود ، لا يمكن التحقق من الثوابت إلا من أجل المساواة.
  
• "المصطلح" عبارة عن مجموعة من العناصر المتعددة. يشيع استخدامها بنفس الطريقة مثل مُنشئي البيانات في Haskell: مُنشئ البيانات (سلسلة) بالإضافة إلى صفر أو أكثر من المعلمات. يستخدم OCanren مُنشئي بيانات منتظمين من OCaml.
  

على سبيل المثال ، إذا كنا نريد العمل مع المصفوفات في miniKanren نفسها ، فيجب أن يتم وصفها من حيث المصطلحات المشابهة للغات الوظيفية - كقائمة مرتبطة منفردة. القائمة إما قائمة فارغة (يشار إليها ببعض المصطلحات البسيطة) ، أو زوج من العنصر الأول من القائمة ("الرأس") وعناصر أخرى ("الذيل").

let emptyList = Nil let list_123 = Cons (1, Cons (2, Cons (3, Nil))) 

برنامج miniKanren هو العلاقة بين بعض المتغيرات. عند بدء التشغيل ، يعطي البرنامج جميع القيم الممكنة للمتغيرات في شكل عام. غالبًا ما تتيح لك التطبيقات الحد من عدد الإجابات في المخرجات ، على سبيل المثال ، ابحث عن الأولى فقط - لا يتوقف البحث دائمًا بعد العثور على جميع الحلول.

يمكنك كتابة العديد من العلاقات التي يتم تعريفها من خلال بعضها البعض وحتى تسمى بشكل متكرر كوظائف. على سبيل المثال ، أدناه نحن بدلا من وظيفة $$$إلحاق (أ ، ب) → مع$تحديد العلاقة $$ : قائمة $$$ج$هو سلسلة من القوائم $$$دولا$و $$$ب$. عادة ما تنتهي الوظائف التي تُرجع العلاقات بـ "o" لتمييزها عن الوظائف العادية.

يتم كتابة العلاقة على أنها عبارة عن بعض الحجج. لدينا أربع عمليات أساسية :

• توحيد أو مساواة (===) لفترتين ، يمكن أن تتضمن المصطلحات متغيرات. على سبيل المثال ، يمكنك كتابة قائمة "العلاقة" $$$ل$يتكون من عنصر واحد $$$x$":
  
  

   let isSingletono xl = l === Cons (x, Nil) 

• الاقتران (المنطقي "و") والانفصال (المنطقي "أو") - كما هو الحال في المنطق العادي. يشار إلى OCanren باسم &&& و |||. ولكن في الأساس لا يوجد إنكار منطقي في MiniKanren.
  
• إضافة متغيرات جديدة. في المنطق ، هو كمي للوجود. على سبيل المثال ، للتحقق من القائمة لعدم وجود إفراغ ، تحتاج إلى التحقق من أن القائمة تتكون من رأس وذيل. هذه ليست حجة للعلاقة ، لذلك تحتاج إلى إنشاء متغيرات جديدة:
  
  

   let nonEmptyo l = fresh (ht) (l === Cons (h, t)) 

يمكن أن تستحضر العلاقة نفسها بشكل متكرر. على سبيل المثال ، تحتاج إلى تحديد عنصر "العلاقة $$$x$يكمن في القائمة ". سنحل هذه المشكلة من خلال تحليل الحالات التافهة ، كما هو الحال في اللغات الوظيفية:

1. أو رئيس القائمة هو $$$x$
   
2. إما $$$x$يكمن في الذيل
   

 let membero lx = fresh (ht) ( (l === Cons (h, t)) &&& (x === h ||| membero tx) ) 

الإصدار الأساسي للغة مبني على هذه العمليات الأربع. هناك أيضًا ملحقات تتيح لك استخدام عمليات أخرى. الأكثر فائدة منها هو عدم المساواة القيد لتحديد عدم المساواة في فترتين (= / =).

على الرغم من بساطتها ، miniKanren هي لغة معبرة تماما. على سبيل المثال ، انظر إلى تسلسل العلائقية لقائمتين. تتحول وظيفة حجتين إلى علاقة ثلاثية " $$$ab$هو سلسلة من القوائم $$$دولا$و $$$ب$".

 let appendo ab ab = (a === Nil &&& ab === b) ||| (fresh (ht tb) (*  :  fresh   &&& *) (a = Cons (h, t)) (appendo tb tb) (ab === Cons (h, tb))) 

لا يختلف الحل من الناحية الهيكلية عن كيفية كتابته بلغة وظيفية. نحن نحلل حالتين توحدهما جملة:

1. إذا كانت القائمة الأولى فارغة ، فستكون القائمة الثانية ونتائج السلاسل متساوية.
   
2. إذا لم تكن القائمة الأولى فارغة ، فسنقوم بتحليلها في الرأس والذيل ونبني النتيجة باستخدام نداء متكرر للعلاقة.
   

يمكننا تقديم طلب لهذه العلاقة ، وتحديد الوسيطة الأولى والثانية - نحصل على تسلسل القوائم:

 run 1 (λ q -> appendo (Cons (1, Cons (2, Nil))) (Cons (3, Cons (4, Nil))) q) 

⇒

 q = Cons (1, Cons (2, Cons (3, Cons (4, Nil)))) 

يمكننا إصلاح الوسيطة الأخيرة - نحصل على جميع أقسام هذه القائمة إلى قسمين.

 run 4 (λ qr -> appendo qr (Cons (1, Cons (2, Cons (3, Nil))))) 

⇒

 q = Nil, r = Cons (1, Cons (2, Cons (3, Nil))) | q = Cons (1, Nil), r = Cons (2, Cons (3, Nil)) | q = Cons (1, Cons (2, Nil)), r = Cons (3, Nil) | q = Cons (1, Cons (2, Cons (3, Nil))), r = Nil 

يمكنك أن تفعل أي شيء آخر. مثال غير قياسي قليلاً ، حيث نقوم بإصلاح جزء فقط من الوسائط:

 run 1 (λ qr -> appendo (Cons (1, Cons (q, Nil))) r (Cons (1, Cons (2, Cons (3, Cons (4, Nil)))))) 

⇒

 q = 2, r = Cons (3, Cons (4, Nil)) 

كيف يعمل؟

من وجهة نظر النظرية ، لا يوجد شيء مثير للإعجاب هنا: يمكنك دائمًا مجرد البدء في البحث عن جميع الخيارات الممكنة لجميع الحجج ، والتحقق من كل مجموعة ما إذا كانت تتصرف فيما يتعلق بوظيفة / علاقة معينة كما نود (انظر "خوارزمية المتحف البريطاني" ) . من الأمور المهمة هنا أن البحث (بمعنى آخر ، البحث عن حل) يستخدم فقط بنية العلاقة الموصوفة ، والتي يمكن أن تكون فعالة نسبيًا في الممارسة العملية.

يتعلق البحث بتجميع المعلومات حول المتغيرات المختلفة في الحالة الحالية. نحن إما لا نعرف أي شيء عن كل متغير ، أو نعرف كيف يتم التعبير عنه من حيث المصطلحات والقيم والمتغيرات الأخرى. على سبيل المثال:

b = Cons (x, y)
c = Cons (10, z)
x = ?
y = ?
z = ?

بالمرور عبر التوحيد ، ننظر إلى فترتين مع مراعاة هذه المعلومات وإما تحديث الحالة أو إنهاء البحث إذا تعذر توحيد فترتين. على سبيل المثال ، عند إكمال التوحيد b = c ، نحصل على معلومات جديدة: x = 10 ، y = z. لكن التوحيد ب = لا شيء سوف يسبب تناقضا.

نحن نبحث في تقاطعات متتالية (بحيث تتراكم المعلومات) ، وفي تقاطع ، نقسم البحث إلى فرعين متوازيين وننتقل ، نتبادل الخطوات بينهما - هذا ما يسمى بحث التشذير. بفضل هذا البديل ، اكتمل البحث - سيتم العثور على كل حل مناسب بعد وقت محدد. على سبيل المثال ، في لغة Prolog هذا ليس كذلك. إنها تفعل شيئًا ما مثل عملية تتبع ارتباطات عميقة (يمكن تعليقها على فرع لا حصر له) ، ويعد البحث المتشابك في الأساس عبارة عن تعديل ارتباط صعب عريض للغاية.

دعونا الآن نرى كيف يعمل الاستعلام الأول من القسم السابق. نظرًا لأن appendo يحتوي على مكالمات متكررة ، فسنضيف فهارس إلى المتغيرات لتمييزها. يوضح الشكل أدناه شجرة التعداد. تشير الأسهم إلى اتجاه نشر المعلومات (باستثناء العائد من التكرار). بين الوصلات ، لا يتم توزيع المعلومات ، وبين الوصلات يتم توزيعها من اليسار إلى اليمين.

1. نبدأ مع مكالمة خارجية إلى appendo. غادر فرع من الانفصال بسبب الجدل: القائمة $$$دولا$ليس فارغا
   
2. في الفرع الأيمن يتم تقديم المتغيرات المساعدة ، والتي تستخدم بعد ذلك "لتحليل" القائمة $$$a_1$على الرأس والذيل.
   
3. بعد ذلك ، تحدث المكالمة العودية appendo لـ = [2] ، b = [3 ، 4] ، ab =؟ ، في أي عمليات مماثلة تحدث.
   
4. ولكن في المكالمة الثالثة إلى appendo لدينا بالفعل = [] ، b = [3،4] ، ab =؟ ، ثم يعمل الاختراق الأيسر فقط ، وبعد ذلك نحصل على المعلومات ab = b. ولكن في الفرع الصحيح هناك تناقض.
   
5. الآن يمكننا كتابة جميع المعلومات المتاحة واستعادة الإجابة عن طريق استبدال قيم المتغيرات:
   
   a_1 = [1, 2]
b_1 = [3, 4]
ab_1 = Cons h_1 tb_1
h_1 = 1
a_2 = t_1 = [2]
b_2 = b_1 = [3, 4]
ab_2 = tb_1 = Cons h_2 tb_2
h_2 = 2
a_3 = t_2 = Nil
b_3 = b_2 = b_1 = [3, 4]
ab_3 = tb_2 = b_3 = [3, 4]

   
6. يتبع ذلك $$$ab_1$= سلبيات (1 ، سلبيات (2 ، [3 ، 4])) = [1 ، 2 ، 3 ، 4] ، كما هو مطلوب.
   

ما فعلت في المرحلة الجامعية

كل شيء يبطئ

كما هو الحال دائمًا: يعدونك بأن كل شيء سيكون إعلانًا فائقًا ، ولكن في الواقع يجب أن تتكيف مع اللغة وأن تكتب كل شيء بطريقة خاصة (مع الأخذ في الاعتبار كيفية تنفيذ كل شيء) من أجل عمل شيء على الأقل ، باستثناء الأمثلة البسيطة. هذا مخيب للآمال.

واحدة من المشاكل الأولى التي يواجهها مبرمج miniKanren المبتدئ هو أنه يعتمد إلى حد كبير على الترتيب الذي تصف فيه الشروط (الملحقة) في البرنامج. مع أمر واحد ، كل شيء على ما يرام ، ولكن تم تبديل اثنين من الوصلات وبدأ كل شيء يعمل ببطء شديد أو لم ينته على الإطلاق. هذا غير متوقع.

حتى في المثال مع appendo ، لا ينتهي التشغيل في الاتجاه المعاكس (توليد انشقاقات القائمة إلى قسمين) إلا إذا حددت صراحة عدد الإجابات التي تريدها (ثم ينتهي البحث بعد العثور على العدد المطلوب).

لنفترض أننا أصلح المتغيرات الأصلية على النحو التالي: a = ؟، B = ؟، Ab = [1، 2، 3] (انظر الشكل أدناه) في الفرع الثاني ، لن يتم استخدام هذه المعلومات بأي شكل من الأشكال أثناء مكالمة متكررة (المتغير ab والقيود على $$$h_1$و $$$tb_1$تظهر فقط بعد هذه المكالمة). لذلك ، عند أول مكالمة متكررة ، ستكون كل الوسائط الخاصة بها متغيرات مجانية. ستؤدي هذه الدعوة إلى إنشاء جميع أنواع الثلاثيات من قائمتين وتسلسلهما (وهذا الجيل لن ينتهي أبدًا) ، ومن ثم سيتم اختيار تلك الدعائم التي ظهر فيها العنصر الثالث بالطريقة التي نحتاجها بالضبط.



كل شيء ليس سيئًا كما قد يبدو للوهلة الأولى ، لأننا سننظم هذه المجموعات الثلاثية في مجموعات كبيرة. القوائم بنفس الطول ولكن العناصر المختلفة لا تختلف عن وجهة نظر الوظيفة ، وبالتالي سوف تقع في حل واحد - سيكون هناك متغيرات مجانية بدلاً من العناصر. ومع ذلك ، سوف نواصل فرز جميع أطوال القوائم الممكنة ، على الرغم من أننا نحتاج إلى واحد فقط ، ونحن نعرف أي منها. هذا استخدام غير منطقي للغاية (عدم استخدام) للمعلومات في البحث.

هذا المثال المحدد سهل الإصلاح: تحتاج فقط إلى نقل المكالمة العودية إلى النهاية وسيعمل كل شيء كما يجب. قبل إجراء مكالمة متكررة ، سيتم التوحيد مع المتغير ab وسيتم إجراء مكالمة متكررة من ذيل القائمة المحددة (كدالة متكررة عادية). هذا التعريف مع مكالمة متكررة في النهاية سوف يعمل بشكل جيد في جميع الاتجاهات: بالنسبة للمكالمات المتكررة ، نتمكن من تجميع كل المعلومات الممكنة حول الوسائط.

ومع ذلك ، في أي مثال أكثر تعقيدًا بقليل ، عندما يكون هناك العديد من المكالمات الهادفة ، لا يوجد ترتيب محدد واحد يكون كل شيء على ما يرام. أبسط مثال: توسيع قائمة باستخدام سلسلة. نصلح الوسيطة الأولى - نحتاج إلى هذا الترتيب المحدد ، ونصلح الوسيطة الثانية - نحتاج إلى تبديل المكالمات. خلاف ذلك ، يتم البحث عنه لفترة طويلة ولا ينتهي البحث.

 reverso x xr = (x === Nil &&& xr == Nil) ||| (fresh (ht tr) (x === Cons (h, t)) (reverso t tr) (appendo tr (Cons (h, Nil)) xr)) 

وذلك لأن عمليات البحث المتداخلة تتقاطع بالتتابع ، ولا يمكن لأحد أن يفكر في كيفية القيام بذلك بشكل مختلف دون أن يفقد الكفاءة المقبولة ، على الرغم من أنهم حاولوا. بالطبع ، سيتم العثور على جميع الحلول في يوم من الأيام ، ولكن بالترتيب الخاطئ ، سيتم البحث عنها لفترة طويلة بشكل غير واقعي بحيث لا يوجد أي معنى عملي في هذا الأمر.

هناك تقنيات لكتابة البرامج لتجنب هذه المشكلة. لكن الكثير منهم يحتاجون إلى مهارة وخيال خاصين للاستخدام ، والنتيجة هي برامج كبيرة جدًا. مثال على ذلك هو مصطلح حدود حجم المصطلح وتعريف التقسيم الثنائي مع الباقي من خلال الضرب بمساعدته. بدلا من كتابة بغباء تعريف رياضي

 divo nmqr = (fresh (mq) (multo mq mq) (pluso mq rn) (lto rm)) 

يجب أن أكتب تعريفًا متكررًا يتكون من 20 سطرًا + وظيفة مساعدة كبيرة غير واقعية للقراءة (ما زلت لا أفهم ما يجري هناك). يمكن العثور عليها في أطروحة ويل بيرد في قسم الحساب الثنائي البحت.

في ضوء ما تقدم ، أود أن أتوصل إلى نوع من تعديل البحث بحيث تعمل البرامج البسيطة والمكتوبة بشكل طبيعي أيضًا.

تحسين

لاحظنا أنه عندما يكون كل شيء سيئًا ، فلن ينتهي البحث إلا إذا أشرت صراحة إلى عدد الإجابات وكسرها. لذلك ، قرروا القتال بدقة مع عدم اكتمال عملية البحث - فمن الأسهل بكثير أن يتم صب الخرسانة من "أنه يعمل لفترة طويلة". بشكل عام ، بالطبع ، أريد فقط تسريع عملية البحث ، ولكن من الصعب للغاية إضفاء الطابع الرسمي عليها ، لذلك بدأنا بمهمة أقل طموحًا.

في معظم الحالات ، عندما يختلف البحث ، يحدث موقف يكون من السهل تتبعه. إذا تم استدعاء دالة بشكل متكرر ، وفي مكالمة متكررة ، تكون الوسائط هي نفسها أو أقل تحديدًا ، ثم يتم استدعاء مهمة فرعية أخرى في المكالمة العودية مرة أخرى ويحدث تكرار غير محدود. من الناحية الشكلية ، يبدو الأمر كالتالي: هناك بديل ، يتم تطبيقه على الحجج الجديدة ، ونحصل على الحجج القديمة. على سبيل المثال ، في الشكل أدناه ، تعتبر المكالمة المتكررة تعميمًا للأصل: يمكنك الاستعاضة عنها $$$c_2 دولا$= [س ، 3] ، $$$d_2 دولا$= س واحصل على المكالمة الأصلية.



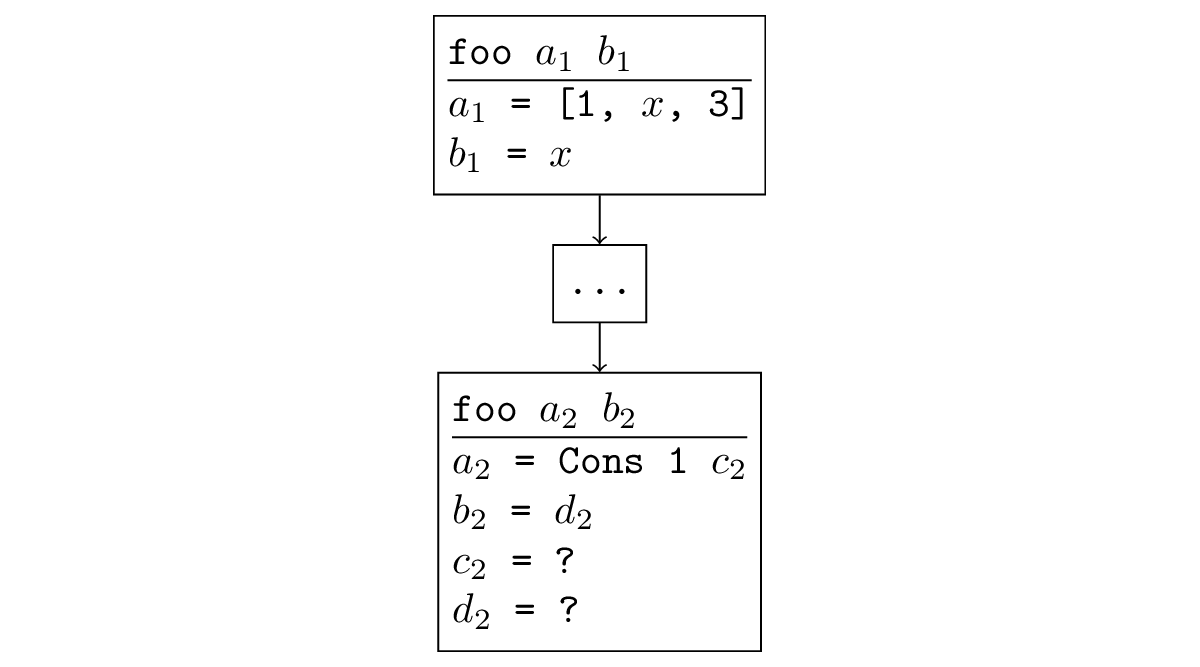
يمكن تتبع هذا الموقف أيضًا في أمثلة الاختلاف التي قابلناها بالفعل. كما كتبت في وقت سابق ، عندما تقوم بتشغيل appendo في الاتجاه المعاكس ، سيتم إجراء مكالمة متكررة مع متغيرات مجانية بدلاً من جميع المتغيرات ، والتي ، بالطبع ، أقل تحديداً من المكالمة الأصلية ، التي تم فيها إصلاح الوسيطة الثالثة.

إذا ركضنا العكس مع س =؟ و xr = [1، 2، 3] ، يمكن ملاحظة أن أول مكالمة متكررة ستحدث مرة أخرى مع اثنين من المتغيرات المجانية ، لذلك من الواضح أنه يمكن نقل وسيطات جديدة مرة أخرى إلى المتغيرات السابقة.

 reverso x x_r  (* x = ?, x_r = [1, 2, 3] *) fresh (ht t_r) (x === Cons (h, t)) (* x_r = [1, 2, 3] = Cons 1 (Cons 2 (Cons 3 Nil))) x = Cons (h, t) *) (reverso t t_r) (* :   t=x, t_r=[1,2,3],    *) 

باستخدام هذا المعيار ، يمكننا اكتشاف الاختلاف في عملية تنفيذ البرنامج ، وفهم أن كل شيء سيء مع هذا الترتيب ، وتغييره ديناميكيًا إلى آخر. بفضل هذا ، من الناحية المثالية ، سيتم اختيار الترتيب الصحيح لكل مكالمة.
يمكنك القيام بذلك بسذاجة: إذا تم العثور على الاختلاف في الملتقى ، فإننا نطرح جميع الإجابات التي وجدها بالفعل ونؤجل تنفيذها في وقت لاحق ، "تخطي إلى الأمام" الاقتران التالي. بعد ذلك ، ربما عندما نواصل تنفيذه ، سيتم بالفعل معرفة المزيد من المعلومات ولن ينشأ الاختلاف. في الأمثلة الخاصة بنا ، سيؤدي هذا إلى تقاطعات التبديل المطلوبة.

هناك طرق أقل سذاجة تسمح ، على سبيل المثال ، بعدم فقدان العمل المنجز بالفعل ، وتأجيل الأداء. بالفعل مع البديل الأكثر غباء وهو تغيير الترتيب ، اختفى الاختلاف في جميع الأمثلة البسيطة التي تعاني من عدم التبادلية للتزامن ، والذي نعرفه ، بما في ذلك:

• فرز قائمة الأرقام (إنه أيضًا إنشاء جميع التباديل في القائمة) ،
  
• بيانو الحسابي والحساب الثنائي ،
  
• جيل من الأشجار الثنائية بحجم معين.
  

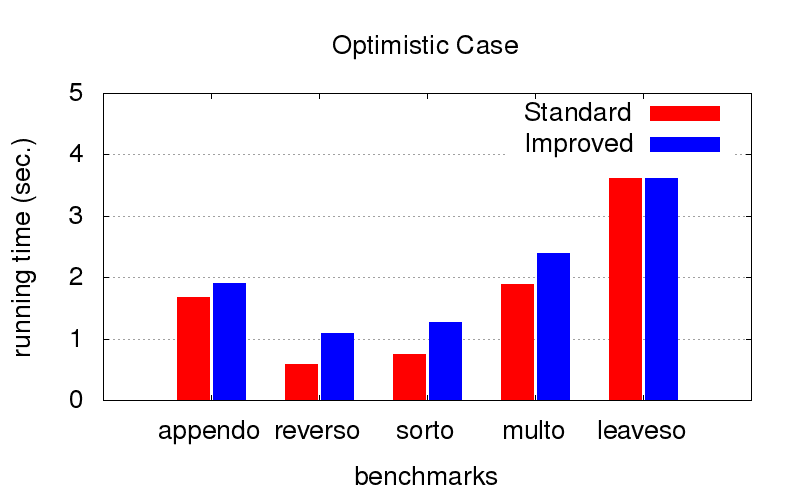
كانت هذه مفاجأة غير متوقعة بالنسبة لنا. بالإضافة إلى الاختلاف ، يكافح التحسين أيضًا ضد تباطؤ البرامج. توضح الرسوم البيانية أدناه وقت تنفيذ البرامج بترتيبين مختلفين بالاقتران (تحدث نسبيًا ، واحد من الأفضل وواحد من بين العديد من العناصر السيئة). تم إطلاقه على جهاز كمبيوتر مع تكوين Intel Core i7 CPU M 620 ، 2.67 جيجاهرتز × 4 ، 8 جيجابايت من ذاكرة الوصول العشوائي مع نظام التشغيل Ubuntu 16.04.

عندما يكون الطلب هو الأمثل بالفعل (نختاره يدويًا) ، يؤدي التحسين إلى إبطاء التنفيذ قليلاً ، ولكن ليس حرجًا


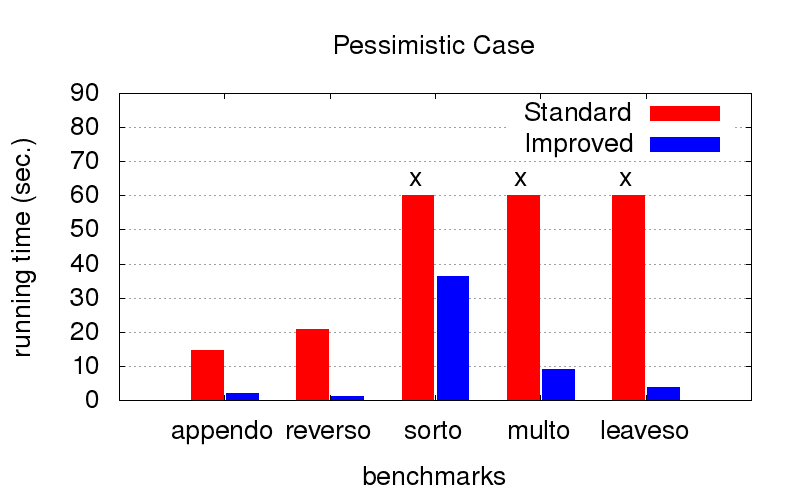
ولكن عندما لا يكون الترتيب الأمثل (على سبيل المثال ، مناسب فقط للتشغيل في الاتجاه المعاكس) ، مع التحسين ، فإنه يصبح أسرع بكثير. تعني الصلبان أننا لا نستطيع الانتظار حتى النهاية ، فهي تعمل لفترة أطول من ذلك بكثير

كيف نكسر شيئا

كل هذا كان مبنياً على الحدس ، وأردنا إثبات ذلك بدقة. النظرية بعد كل شيء.

من أجل إثبات شيء ما ، نحتاج إلى دلالات رسمية للغة. وصفنا دلالات التشغيل ل miniKanren. هذا هو نسخة مبسطة وحسابية لتطبيق لغة حقيقية. يستخدم إصدارًا محدودًا جدًا (وبالتالي سهل الاستخدام) ، حيث يمكنك فقط تحديد التنفيذ النهائي للبرامج (يجب أن يكون البحث نهائيًا). ولكن لأغراضنا هذا هو بالضبط ما هو مطلوب.

لإثبات المعيار ، يتم صياغة lemma أولاً: تنفيذ البرنامج من حالة أكثر عمومية سيعمل لفترة أطول. بشكل رسمي: شجرة الإخراج في الدلالات لها ارتفاع كبير. تم إثبات ذلك من خلال الحث ، ولكن يجب تعميم العبارة بعناية فائقة ، وإلا لن تكون الفرضية الاستقرائية قوية بدرجة كافية. ويترتب على هذا lemma أنه إذا كان المعيار يعمل أثناء تنفيذ البرنامج ، فإن شجرة الإخراج لها شجرة فرعية خاصة بها ذات ارتفاع أكبر أو مساوي. هذا يعطي تناقضًا ، نظرًا لأن الدلالات المعطاة بشكل تعريفي تكون جميع الأشجار محدودة. هذا يعني أنه في دلالاتنا ، فإن تنفيذ هذا البرنامج غير واضح ، مما يعني أن البحث فيه لا ينتهي.

الطريقة المقترحة متحفظة: نحن نغير شيئًا فقط عندما نكون مقتنعين بأن كل شيء سيئ بالفعل تمامًا ومن المستحيل أن يفعل ما هو أسوأ ، وبالتالي فإننا لا نكسر أي شيء من حيث إكمال البرنامج.

يحتوي الدليل الرئيسي على الكثير من التفاصيل ، لذلك كانت لدينا رغبة في التحقق منه رسميًا عن طريق الكتابة إلى Coq . ومع ذلك ، فقد تبين أن الأمر صعب للغاية من الناحية الفنية ، لذلك فقد تهدأ حماستنا وشاركنا بجدية في التحقق التلقائي فقط في القضاء.

نشر

في منتصف العمل ، قدمنا ​​هذه الدراسة في جلسة الملصقات الخاصة بـ ICFP-2017 في مسابقة أبحاث الطلاب . التقينا هناك بمبدعي اللغة - ويل بيرد ودانييل فريدمان - وقالوا إنها ذات مغزى ونحن بحاجة إلى النظر فيها بمزيد من التفصيل. بالمناسبة ، سيكون Will صديقًا بشكل عام مع مختبرنا في JetBrains Research. بدأت جميع أبحاثنا حول miniKanren عندما ، في عام 2015 ، سوف يعقد مدرسة صيفية في البرمجة العلائقية في سان بطرسبرغ.

بعد مرور عام ، أوصلنا عملنا إلى شكل أكثر أو أقل اكتمالًا وقدمنا المقالة في مبادئ وممارسات البرمجة التصميمية 2018.

ماذا أفعل في كلية الدراسات العليا

أردنا الاستمرار في الانخراط في دلالات رسمية ل miniKanren وإثبات صارم لجميع خصائصه. في الأدب ، عادة ما يتم افتراض الخصائص وإظهارها باستخدام الأمثلة ، ولكن لا أحد يثبت أي شيء. على سبيل المثال ، الكتاب الرئيسي عن البرمجة العلائقية هو قائمة بالأسئلة والأجوبة ، يخصص كل منها لرمز معين. حتى بالنسبة لبيان اكتمال البحث المتشابك (وهذه واحدة من أهم مزايا miniKanren عبر Prolog القياسي) ، فمن المستحيل العثور على صيغة صارمة. لا يمكننا العيش على هذا النحو ، قررنا ، وبعد تلقينا نعمة من الإرادة ، بدأنا العمل.

اسمحوا لي أن أذكركم بأن الدلالات التي قمنا بتطويرها في المرحلة السابقة كان لها قيود كبيرة: تم وصف البرامج ذات البحث المحدود فقط. في miniKanren ، تعد البرامج قيد التشغيل ممتعة أيضًا حيث يمكنها إدراج عدد لا حصر له من الإجابات. لذلك ، كنا بحاجة إلى دلالات أكثر باردة.

هناك العديد من الطرق القياسية المختلفة لتحديد دلالات لغة البرمجة ، وكان علينا فقط اختيار واحد منهم وتكييفها مع حالة معينة. لقد وصفنا الدلالات كنظام انتقال موسوم - مجموعة من الحالات المحتملة في عملية البحث والانتقالات بين هذه الحالات ، بعضها مُعلّم ، مما يعني أنه في هذه المرحلة من البحث ، تم العثور على إجابة أخرى. وبالتالي يتم تحديد تنفيذ برنامج معين من خلال تسلسل هذه التحولات. يمكن أن تكون هذه التسلسلات محدودة (تأتي إلى حالة طرفية) أو لا حصر لها ، وتصف البرامج التي يتم إنهاؤها في وقت واحد وعدم استكمالها. من أجل تحديد مثل هذا الكائن رياضيا بالكامل ، يحتاج المرء إلى استخدام تعريف متزامن.

دلالات أعلاه و تعمل - أنه يعبر عن تنفيذ البحث الحقيقي. بالإضافة إلى ذلك ، نستخدم أيضًا دلالات الدلالة ، التي تربط بعض الأشياء الرياضية بالبرامج الطبيعية في البرامج اللغوية والإنشاءات (على سبيل المثال ، تُعتبر العلاقات في برنامج ما بمثابة علاقات على مجموعة متنوعة من المصطلحات ، والتزامن هو تقاطع للعلاقات ، وما إلى ذلك). تُعرف الطريقة القياسية لتعريف مثل هذه الدلالات بأنها أصغر نموذج لإربان ، وقد تم فعل ذلك بالفعل في وقت مبكر (أيضًا في مختبرنا) بالنسبة لـ miniKanren.

بعد ذلك ، يمكن صياغة اكتمال البحث في اللغة ، جنبًا إلى جنب مع صحتها ، على أنه تكافؤ لهذين الدلالات - تزامن مجموعات الإجابات لبرنامج معين فيها. تمكنا من إثبات ذلك. من المثير للاهتمام (والمحزن بعض الشيء) أننا فعلنا دون الاستقراء ، وذلك باستخدام العديد من الحث المتداخل مع معايير مختلفة.
كنتيجة طبيعية ، نحصل أيضًا على صحة بعض التحولات اللغوية المفيدة (من حيث مجموعة الحلول التي تم الحصول عليها): إذا كان التحول من الواضح أنه لا يغير الكائن الرياضي المقابل ، على سبيل المثال ، إعادة ترتيب الوصلات أو استخدام الوصلات التوزيعية أو الوصلات ، فلن تتغير نتائج البحث.

الآن نريد استخدام الدلالات لإثبات الخصائص المفيدة الأخرى للغة ، على سبيل المثال ، معايير اكتمال / التباعد أو صحة إنشاءات لغة إضافية.

لقد ألقينا نظرة أكثر تفصيلاً على وصف دقيق لإضفاء الطابع الرسمي لدينا باستخدام Coq. بعد التغلب على العديد من الصعوبات المختلفة واستثمار الكثير من الجهد ، تمكنا في الوقت الحالي من وضع دلالات تشغيلية للغة وإجراء بعض الأدلة ، والتي كان شكلها على ورقة "بوضوح. سؤال " نحن لا نفقد الثقة في أنفسنا.