🐂 ↘️ 🧔🏾 Wolfensteiny 3D - الهندسة العكسية 251 بايت من جافا سكريبت 🚴 🥋 📰

عند كتابة التعليمات البرمجية ، لا يفكر الكثيرون في أي شيء آخر غير منطق البرنامج نفسه. قلة من الناس يفكرون في تحسين الكود بمرور الوقت ، من الذاكرة. ولكن فقط عدد قليل يصل إلى المستوى الأخير - ضغط البرنامج إلى حجم صغير قياسي.

انظر ، على سبيل المثال ، نتيجة 251 بايت فقط من JavaScript:

حسنًا ، لنكتشف كيف يعمل!

من اين هو؟

يوجد هذا الكود ، بالإضافة إلى الكثير مما التفت إليه في هذه المقالة ، على موقع p01.org الخاص بماتيو 'p01' الرائع ، هنري ، مطور جافا سكريبت ، وغالبًا ما لا يشارك في ضغط الكود إلى أحجام مستحيلة. مصدر المواد من هذه المادة هنا .

لذلك ، قبل أن تكون 251 بايت من شفرة المصدر.

<body onload=E=c.getContext("2d"),setInterval(F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,bd?4:D/2,D/2))for(D=0;'.'<F[D*y/hD/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1",t=h=75)><canvas id=c>

من الواضح أن لا شيء واضح.

جعل رمز للقراءة

أولاً وقبل كل شيء ، قمت بوضع كود JavaScript في علامة منفصلة ، للراحة.

يمكن ملاحظة أن المتغيرات E و h و Q و F وغيرها هي ثوابت يمكن استبدالها بقيمها / كائناتها نفسها ، وكذلك تغيير الأسماء.

 var context = c.getContext("2d") var F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,bd?4:D/2,D/2))for(D=0;'.'<F[D*y/hD/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1" var t = 75 var size = 75 function render(){ t += 0.2; c.height=300; for(let x = size; x--;) for(let y = size; y--; context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2)) for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1 } setInterval(render, 75);

هنا ، تم نقل الكود من السلسلة إلى الوظيفة بالفعل ، والسلسلة نفسها لم تمس ، سنحتاجها في المستقبل.

الآن تحويل الحلقات الخارجية اثنين إلى while .

 function render(){ t += 0.2; c.height=300; let x = size; while(x > 0){ let y = size; while(y > 0){ for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1 context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2); y--; } x--; } }

كيف نرى هذا؟

دعونا نفهم لماذا نرى ذلك على الإطلاق. إذا نظرت إلى الصورة مرة أخرى ، يمكنك فهم الكثير.

صورة قابلة للنقر

هنا ما نراه:

وكلما كان الموضوع أكثر قتامة
يتم غمر الجزء المائل من العقبات التي واجهتها بشكل مختلف مع خطوط ، وليس النقاط.

في الكود ، ينعكس الرسم كما يلي:

 // ,  ,       //   ||     // | | || | | // ↓ ↓ ↓↓ ↓ ↓ context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2);

لماذا نرى أشياء الحجمي في هذا الطوف من النقاط السوداء؟ بعد كل شيء ، يجب أن نكون راضين بظلال مختلفة من الأسود فقط - حجم النقاط السوداء (لا يمكننا تغيير اللون ، E.fillStyle طويل جدًا!). في الواقع ، إنه يعمل ببساطة لأنه في صورة ثنائية الأبعاد ، تعتمد أعيننا بشكل أساسي على ظل الإضاءة وساطتها.

تخيل نفسك تمشي على طول ممر مظلم مع مصباح يدوي فقط في يديك. أنت تلمع أمامك وترى أن بعض الأشياء أقرب وأكثر إشراقًا (مصباح يدوي يضيء ، عقبة مشرقة ، لا توجد ظلال) ، بينما البعض الآخر يكون أكثر قتامة وأغمق (الضوء مبعثر ، ضعيف ، ونرى الظلام - ونحن نشعر بالمسافة). حتى هنا - كلما كان الكائن ( D أكبر) ، كلما كبر الحجم ، نرسم مربعًا أسود على الشاشة.
ولكن كيف نعرف ما الذي يجب أن يكون مشرقًا وما هو غير ذلك؟

عد بكسل

الآن دعونا نتعامل مع هذا الوحش:

 for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1

هكذا كل هذا التعبير عبارة عن خوارزمية ثابتة لخطأ الأشعة تتيح لك العثور على تقاطع الحزمة مع الكتل. لكل بكسل من الشاشة ، نطلق حزمة ، ونتابعها بخطوة ثابتة قدرها 0.1 ، وبمجرد أن نواجه عقبة ، ننهي الخوارزمية ونرسم بكسل على الشاشة ، ونعرف المسافة إلى العقبة.

دعنا نبدأ قراءة هذا الرمز في أجزاء.

الحالة D * y / size - D / 2 | 0 يمكن تمثيل D * y / size - D / 2 | 0 كـ

D * (f r a c y s i z e - f r a c 12) = D * (f r a c y - s i z e / 2 s i z e) < 1

$D * (\ frac {y} {size} - \ frac {1} {2}) = D * (\ frac {y - size / 2} {size}) <1$ ، ثم يُظهر التعبير الموجود بين قوسين "الانحراف" y من وسط الشاشة (في كسور الشاشة). لذلك نحن نحاول أن نفهم ما إذا كانت الحزمة بين الأرض والسقف أم لا. لذلك ، إذا لمسنا الكلمة (أو السقف) ، فسنخرج من الحلقة إلى أبعد من ذلك ، لرسم ورسم بكسل.
وإذا لم نلمسها ، فسنستمر في إجراء العمليات الحسابية: نحن نبحث عن الإحداثيات الحالية للشعاع.

 var T = x / size - .5 + Math.cos(t) / 8; // Math.cos(t)   //    var xcoord = t + depth * Math.cos(T); var ycoord = 3.5 + depth * Math.cos(T - 8); //

لماذا كوس (تي - 8)؟

لذلك اتضح ذلك

c o s (x - 8) a p p r o s i n s i n (x)

$cos (x-8) \ appro sin sin (x)$ بدقة 0.15 راديان. كل ذلك بسبب

f r a c 5 p i 2 a p p r o x 8.15 a p p r o x 8

$\ frac {5 \ pi} {2} \ approx 8.15 \ approx 8$

وبعد ذلك

c o s (a l p h a - 8) a p p r o x c o s (a l p h a - f r a c 5 p i 2) = c o s (a l p h a - f r a c p i 2) = s i n (a l p h a)

$cos (\ alpha-8) \ approx cos (\ alpha- \ frac {5 \ pi} {2}) = cos (\ alpha - \ frac {\ pi} {2}) = sin (\ alpha)$

يجدر الحديث عن كيفية التحقق من نقطة في الفضاء للحصول على كتلة بشكل عام. البطاقة نفسها مأخوذة من الكود المصدري ( F ) وتبدو كما يلي:

 t+=.2,Q= ----> ░█░█░█░░ Math.cos ----> ░░░░█░░░ ;c.heigh ----> ░░█░░░░░   - t=300;fo ----> ░░░░░░░░ <----  , r(x=h;x- ----> ░█░░░░░█     -;)for(y ----> █░█░░░█░ =h;y--;E ----> ░░░░██░░ .fillRec ----> █░░░░░░░

لذلك يبدو وكأنه في الحركة ، يشار إلى مجال رؤية الكاميرا هنا.

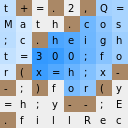
تلك الخلايا التي يكون رمز رمزها أقل من رمز النقطة - "." يتم تمييزها باللون الداكن "." - أي ، الأحرف !"#$%&'()*+,-. الآن ، نقرب إحداثيات الحزمة ، ونحاول معرفة ما إذا كانت الرسالة في هذه" الإحداثيات "مظلمة (عقبة) أم لا (نطير الشعاع أكثر).

نظرًا لأن الفهرس واحد ، والإحداثيات ثنائية ، فإننا نستخدم الاختراق:

 var boxIndex = xcoord & 7 | ycoord << 3;

نتيجة لذلك ، نحصل على رقم يعكس رقم الكتلة (جيدًا ، أو فراغات).

دعنا نعود إلى الرمز. الآن يبدو لائق.

الكود قليل الدسم

 function render(){ t += 0.2; c.height=300; let x = size; while(x > 0){ let y = size; while(y > 0){ var depth = 0 while(depth < 8){ depth += 0.1 var T = x / size - .5 + Math.cos(t) / 8; //   var isFloorOrCeiling = depth * y / size - depth / 2 | 0; //      ? if(isFloorOrCeiling) break; var xcoord = t + depth * Math.cos(T) & 7; var ycoord = 3.5 + depth * Math.sin(T); // cos - 8 -> sin boxIndex = xcoord | ycoord << 3; //     , //    if ('.' >= F[boxIndex]) break; b = xcoord; //  ?  ! } context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2) y--; } x--; } }

العودة إلى الرسم

لماذا نحتاج كل هذا؟ الآن ، بعد تنفيذ هذه الخوارزمية ، نعرف المسافة إلى الكائن ، ويمكننا رسمها. ولكن يبقى سؤال واحد دون إجابة: كيف نميز السقف عن وحدة منفصلة؟ بعد كل شيء ، فإن المسافة إلى السقف والكتلة هي الأرقام التي لا تختلف! في الواقع ، لقد أجبنا بالفعل على هذا السؤال.

 // ,  ,      // || // ↓↓ context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2);

هناك شرط واحد في الكود المتعلق بالمتغير b ، ويؤثر على عرض "البيكسل الأسود الكبير": b - xcoord ? 4 : depth / 2 b - xcoord ? 4 : depth / 2 . دعنا نزيل هذا الشرط ونرى ما يحدث بدونه:

لا توجد حدود بين الكتل والسقف! (قابل للنقر)

الشرط b - xcoord سيعطينا عرضًا ثابتًا عندما يكون التغيير الإحداثي 0. ومتى لا يمكن أن يحدث هذا؟ لا يحدث هذا فقط عندما لا نصل إلى السطر (2) في الكود:

 // .... var xcoord = t + depth * Math.cos(T) & 7; // <---    (1) // ... if ('.' >= F[boxIndex]) // <---    (3) break; b = xcoord; // <---     (2) // ....

هذا يعني أن البرنامج يخرج من الدورة في وقت مبكر ، على الخط (3) ، عندما تدخل الحزمة في كتلة غير شفافة في الاتجاه العمودي تقريبًا إلى جدارها ، أي أنها تقع في الوجه "الوجه" للكتلة. وبالتالي ، جميع الكتل تختلف عن الكلمة والسقف.

لذلك ، هذه هي الطريقة التي تظهر بها هذه الصورة ثلاثية الأبعاد الجميلة ، والتي لا ترضي العين فحسب ، بل تجعلك تفكر أيضًا في كيفية ولماذا تعمل. يمكنك رؤية هذا الكود في العمل هنا (متوقف. موقع مطور هذه المعجزة).

Wolfensteiny 3D - الهندسة العكسية 251 بايت من جافا سكريبت

جعل رمز للقراءة

كيف نرى هذا؟

عد بكسل

العودة إلى الرسم

More articles: