فركتلات بأعداد غير عقلانية

هذه المقالة هي استمرار لمقالتي الأولى ، فركتلات في الأعداد الأولية .

المقال التالي: فركتلات بأرقام غير عقلانية. الجزء 2



في مقال سابق ، تعلمنا كيفية رسم أنماط متشابهة ذاتياً باستخدام أعداد أولية متبادلة. في هذه المقالة سأظهر الطبيعة الكسرية للرقم $$$\ sqrt {2}$ .
بدون مقدمة. تحت القط.

سوف نحدد المصطلحات والتدوين. في الرياضيات ، تسمى الأنظمة الموضحة أدناه البلياردو . كذلك سوف نستخدم هذا المصطلح. سيتم الإشارة إلى أبعاد البلياردو المستطيل بواسطة $$$M$ (العرض) و $$$N$ (الطول).

البلياردو الثنائية

في المقال السابق ، أخذنا البلياردو مستطيلة مع الجانبين $$$M$ و $$$N$ ، أطلق كرة فيه ووضع علامة على المسار بخط متقطع عبر الخلية:



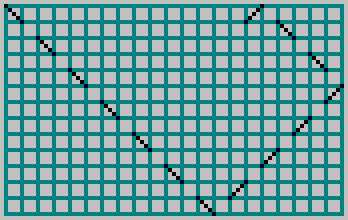
للبساطة المتبادلة $$$M$ و $$$N$ نحصل على النمط:



في الإصدار الثنائي ، نحتفل بالمسار ليس بخط متقطع ، ولكننا نرسم الخلايا بالتناوب باللونين الأسود والأبيض (نقوم بتشكيل صفيف ثنائي ، ونضع 0 للأسود و 1 للأبيض في الخلية المقابلة):



قواعد انعكاس الحدود:



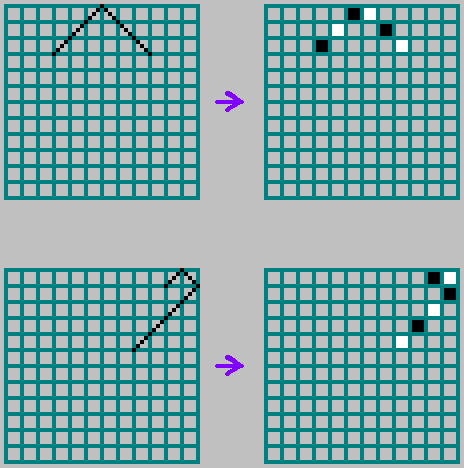
للبساطة المتبادلة $$$M$ و $$$N$ يمر المسار عبر كل خلية:




إذا كان لدى الأطراف مقسوم مشترك ، فإن الكرة تدخل الزاوية قبل أن تمر عبر كل خلية:



أنها مريحة للنظر في هذه القضية والبلياردو في مستطيل مع الجانبين $$$\ frac {M} {GCD}$ و $$$\ frac {N} {GCD}$ (GCD هي أكبر عامل مشترك):



قبل الانتقال ، املأ الجدول الذي اقترحه المستخدم Captain1312 في مقالته (سنقوم بتقسيم جوانب البلياردو إلى GCD).

$$$(1 ، 0)$ قليلا

لكل طاولة بلياردو $$$M$ و $$$N$ تأخذ قليلا مع الإحداثيات $$$(1 ، 0)$ .



إذا $$$M$ هو مقسم $$$N$ - ثم قليلا مع الإحداثيات $$$(1 ، 0)$ مفقود ( $$$\ frac {M} {GCD} = 1$ ) في هذه الحالة ، نأخذ الشيء المقلوب مع الإحداثيات $$$(0 ، 1)$ .

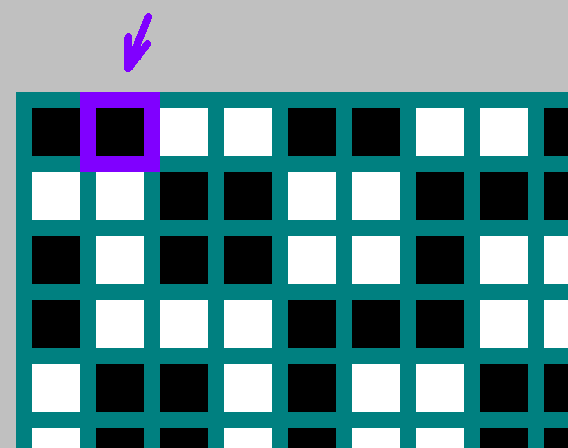
املأ الجدول. الأصل هو الزاوية اليسرى العليا. بواسطة $$$x$ - عرض البلياردو $$$M$ بواسطة $$$ذ$ - الطول $$$N$ . لكل البلياردو نحتفل قليلا $$$(1 ، 0)$ ، أو قليلا مقلوب $$$(0 ، 1)$ (سنعود إلى هذا الموضوع أدناه).

تسلسل ثنائي

لماذا عكسنا بعض الشيء عند عرض البلياردو $$$M = 1 دولا$ ؟ للبساطة المتبادلة $$$M$ و $$$N$ يمر مسار الكرة عبر كل خلية. بين الجدران العليا واليسرى للبلياردو ، تمر الكرة في كل مرة بعدد من الخلايا.





البتات في العمود الأيسر هي البتات المقلوبة من الصف العلوي. نحن لا نأخذ الصفر بت - المسار يبدأ به:



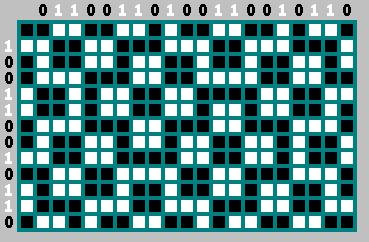
بالإضافة إلى ذلك ، يمكننا أن نرمي بأمان كل ثانية من هذا التسلسل (بت $$$2_ {n-1}$ - قليلا مقلوب $$$2_ {n}$ ):



حصلت على التسلسل $$ للبلياردو $$$(21،13) دولا$ . التسلسل فريد من نوعه للجميع. $$$M$ و $$$N$ .

مهما كان الارتفاع $$$N$ لم نأخذها - الكرة تسير دائمًا على طول المسار $$$2N$ بين اثنين من انعكاسات من الجدار العلوي. من الجدار العلوي ، تبدأ الحركة دائمًا بحرف "0" (خلية سوداء) وتنتهي بحرف "1" (خلية بيضاء):



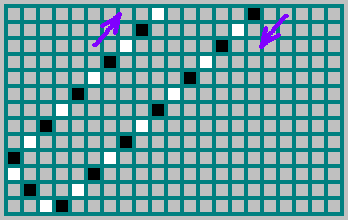
في الواقع ، تسلسل (الذي أبرزنا أعلاه - $$ يظهر على أي جانب وصلت الكرة في: 1 - إذا حلقت الكرة في المنعكس ، وانعكست من الجدار الأيمن و 0 - إذا حلقت الكرة في المنعكس من الجدار الأيسر. في الصورة ، يتم تحديد مسار الكرة باللون الأسود إذا تحركت الكرة إلى اليمين والأبيض إذا تحركت إلى اليسار:




هذا التسلسل ( $$ ) يحتوي على جميع المعلومات اللازمة عن النمط. باستخدامه ، يمكننا استعادة النموذج الأصلي (وحتى النظر إلى ما وراء الحد السفلي للنمط). تأخذ مربع مع الجانبين $$$M$ . نرتب بتات التسلسل لدينا في تلك الأماكن التي تضرب فيها الكرة الجدار العلوي (المسافة بين اللمسات المجاورة للكرة هي خليتان).



إذا كانت البتة المقابلة = 1 - نبدأ في التحرك إلى اليسار ، مع تحديد المسار من خلال الخلية. إذا بت = 0 - انتقل إلى اليمين.



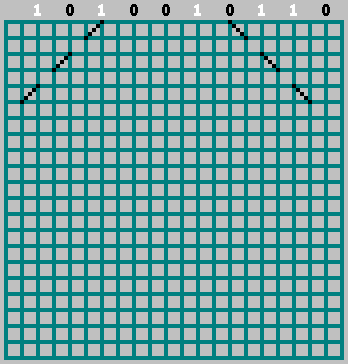
في هذه الحالة ، لا تنس أمر الصفر:



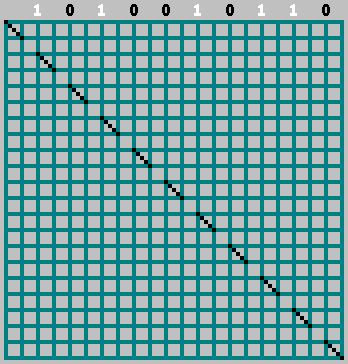
GIF:



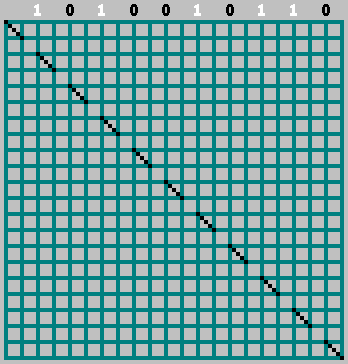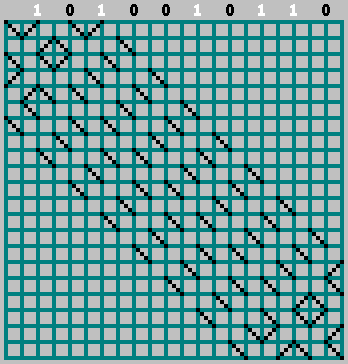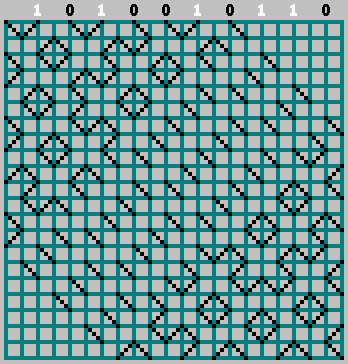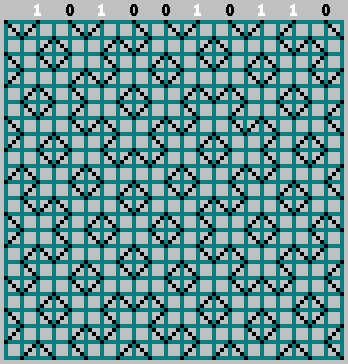
لقد حصلنا على النموذج الأصلي (ونظرنا إلى ما وراء الحد السفلي):



البرنامج النصي لتصور تسلسل ثنائي

يمكننا بناء هذا التسلسل باستخدام بقية التقسيم.

البلياردو أحادي البعد

على المحور العددي $$$X$ خذ نقطتين: $$$0$ و $$$M$ .



الانتقال من نقطة إلى أخرى ، وقياس المسافة $$$N$ :



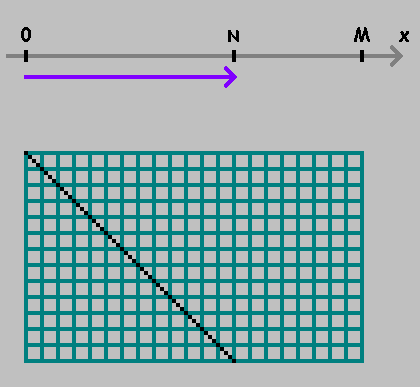
تميزت النقطة. نستمر في قياس المسافة من هذه النقطة ، والحفاظ على الاتجاه. إذا كنت قد وصلت إلى هذه النقطة $$$0$ او $$$M$ - تغيير الاتجاه:



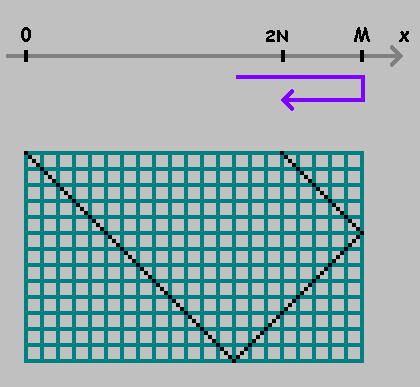
كما هو مبين في الأشكال أعلاه ، فإن النقطة الأولى توضح المكان الذي تمس فيه الكرة الجدار السفلي للبلياردو. هذه النقطة لا تهمنا. سنقوم فقط بإصلاح النقاط $$$2kN دولا$ ل $$$k = 0،1،2 ، ...$ .

كيف نحتفل بهذه النقاط؟ تحويل البلياردو لدينا على المحور $$$X$ . بمناسبة النقاط $$$0 ، M ، 2M ، 3M ، ...$ . الآن الوصول إلى هذه النقطة $$$M$ نحن لا نغير اتجاه الحركة ، ولكن نواصل التحرك إلى هذه النقطة $$ .



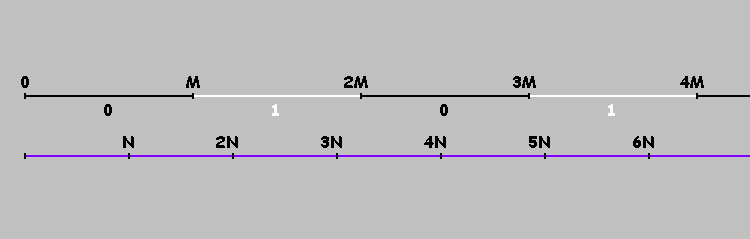
مضاعفات $$$M$ ، قسّم محورنا إلى شرائح. نحن نحتفل بوضع علامة مشروطة على هذه الأجزاء بأخرى والأصفار (بالتناوب). على الأجزاء التي تحمل علامة أصفار ، تنتقل الكرة (في لعبة البلياردو المستطيلة) من اليسار إلى اليمين. على القطاعات التي تحمل علامة - من اليمين إلى اليسار. أو أبسط: الكرة تتحرك من اليسار إلى اليمين إذا $$ ل

$$

$$Q_k = \ lfloor \ frac {2kN} {M} \ rfloor \؛ (\ textrm {mod} \؛ 2) ؛ \ quad k = 0،1،2 ، ...$$

(يجب إيلاء اهتمام خاص لهذه الصيغة. بعد ذلك ، سنعود إليها)

من السهل أن نرى أن النقطة التي عندها لمست الكرة الجدار العلوي للبلياردو هي بقية التقسيم $$$2kN دولا$ على $$$M$ . في هذه الحالة ، لا يمكننا إصلاح حركة الكرة في الاتجاه المعاكس. نأخذ الجزء كله من التقسيم $$$2kN دولا$ على $$$M$ إذا كان الأمر كذلك - فإننا نعتبر بقية التقسيم $$$2kN دولا$ على $$$M$ . اقسم الباقي الناتج على 2 (المسافة بين نقاط الاتصال المجاورة هي خليتين). حصلت على مؤشرات عناصر الصفيف ، والتي نحتاج إلى تعبئتها بالأصفار. تمتلئ العناصر المتبقية بوحدات (الكرة تتحرك من الجدار الأيمن إلى اليسار).

طول التسلسل = $$$\ frac {M} {2}$ .

function sequence(m,n){ var md=m/2; var array=[]; for(var k=0;k<md;k++) array[k]=1; for(var k=0;k<md;k++) if(Math.floor(2*k*n/m)%2==0) array[((2*k*n)%m)/2]=0; return array; } console.log(sequence(55, 34).join('')); // -> 0101001011010010110101101001 

الآن يمكننا بناء تسلسل ثنائي للبلياردو مع أي جانب $$$M$ و $$$N$ (بالأعداد الطبيعية).
بعض الأمثلة:
144 × 89 (أرقام فيبوناتشي):
010100101101001011010110100101101001010010110100101101011010010110100101

169 × 70 (أرقام Pell):
0101011010100101011010100101011010110101001010110101001010110101001010010101101010010

233 × 55 (أرقام فيبوناتشي الفردية $$$F_n$ و $$$F_ {n-3}$ ):
0100100110110110010011011011001001001101100100100110110010010011011011001001101101100
10010011011001001001101100100100


لدينا تسلسل. وإلا كيف يمكنك تصور تسلسلات ثنائية؟ باستخدام سلحفاة الرسومات .

رسومات السلاحف

ارسم خط بعد ذلك ، نأخذ البتات بالتناوب من تسلسلنا. إذا كانت bit = 1 - أدر الجزء ذي الصلة بالجزء السابق $$$60 ^ {\ circ}$ (في اتجاه عقارب الساعة). إذا بت = 0 - اقلب القطعة بواسطة $$$-60 ^ {\ circ}$ . بداية الجزء التالي هي نهاية الجزء السابق.



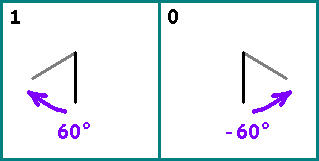
خذ رقمين كبيرين فيبوناتشي: $$$F_ {29} = 514229$ و $$$F_ {28} = 317811$ .

بنيت التسلسل:
00101101001011010010100101101001011010110100101101001010010110100101 ... (257114 حرفًا بالإضافة إلى صفر بت).

نحن تصور باستخدام رسومات السلاحف. حجم القطعة الأولية هو 10 بكسل (الشريحة الأولية في الزاوية اليمنى السفلى):



حجم الجزء الأولي هو 5 بكسل:



حجم الجزء الأولي هو 1 بكسل:



المثال التالي هو أرقام بيل.

$$

$$P_n = \ start {cases} 0، n = 0؛ \\ 1، n = 1 \\ 2P_ {n-1} + P_ {n-2}، n> 1 \ end {cases}$$

خذ $$$P_ {16} = 470832$ و $$$P_ {15} = 195025$ .

التسلسل:
0010100101011010100101011010100101001010110101001010110101000010101101 (235415 حرفًا بالإضافة إلى صفر بت).

حجم الجزء الأولي هو 1 بكسل:



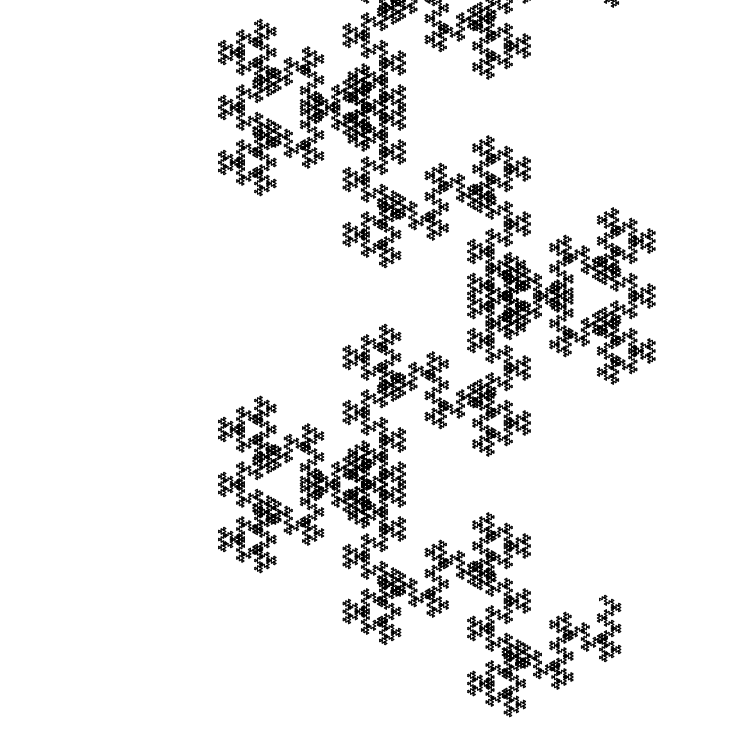
مثال آخر هو أرقام فيبوناتشي الفردية $$$F_n$ و $$$F_ {n-3}$ .
خذ $$$F_ {28} = 317811$ و $$$F_ {25} = 75025 دولا$ .
التسلسل:
00110110010010011111001001001001101101100100110110110010010011011011001001 ... (158905 plus zero bit).
بدلا من الزوايا $$$60 ^ {\ circ}$ و $$$-60 ^ {\ circ}$ سوف نستخدم الزوايا $$$90 ^ {\ circ}$ و $$$-90 ^ {\ circ}$ .
حجم الجزء الأولي هو 5 بكسل:



حجم الجزء الأولي هو 0.4 بكسل:



هذا المنحنى له اسم - " كلمة فيبوناتشي كسورية ". يُعرف بعد Hausdorff لهذا المنحنى:

$$

$$D = 3 {\ frac {\ log \ Phi} {\ log (1 + {\ sqrt {2}})}} = 1،6379؛ \ quad \ Phi = \ frac {1 + {\ sqrt {5}}} {2}$$

البرنامج النصي لتصور تسلسل ثنائي باستخدام سلحفاة الرسومات

المشكلة

هل من الممكن رسم نمط للبلياردو ، الذي لا يمكن تعويض جانبه (أحد الجانبين هو رقم غير عقلاني)؟ المهمة ليست تافهة. في محاولة لحل هذه المشكلة ، سنواجه عددًا من الأسئلة:

1. إذا كانت الأطراف غير قابلة للتطبيق - فلا يمكننا تمهيد البلياردو بخلايا من نفس الحجم.
2. إذا كانت الجوانب غير قابلة للتطبيق - فستنعكس الكرة بلا حدود ولن تضرب الزاوية مطلقًا.
3. تمتلئ التسلسل في البلياردو ليس بالترتيب ، ولكن بشكل عشوائي.



السؤالان الأوليان ، بالطبع ، ليس لديهم حل. ولكن إذا كانت هناك طريقة لملء التسلسل بالترتيب ، فيمكننا ، في التسلسل من اليسار إلى اليمين ، استعادة النموذج بالطريقة التي استخدمناها أعلاه. وبالتالي لنرى كيف يبدو النموذج في الركن الأيسر العلوي من البلياردو ، والتي لا يمكن تعويض جوانبها.

السحر الاسود

خذ البلياردو ، التي تساوي جوانبها أرقام فيبوناتشي (مع أرقام أخرى ، قد لا تنجح هذه الخدعة). قم بتشغيل الكرة داخلها وحدد عدد الكرة التي تلمس الجدار العلوي. املأ الأرقام باللون الأبيض - إذا تحركت الكرة من اليمين إلى اليسار والأسود - إذا كانت الكرة قد انتقلت من اليسار إلى اليمين:



اللون الأبيض يتوافق مع واحد في التسلسل ، أسود - صفر. الآن دعنا نرتب الأرقام بالترتيب:



لقد حصلنا بالضبط على نفس تسلسل الأصفار والأصفار.


في الواقع ، في بعض الحالات ، لا نحتاج إلى أخذ بقية التقسيم. بالنسبة لأرقام فيبوناتشي ، يكفي التحقق من تكافؤ الجزء الصحيح من القسم $$$2kN دولا$ على $$$M$ :

$$

$$Q_k = \ lfloor \ frac {2kN} {M} \ rfloor \؛ (\ textrm {mod} \؛ 2) ؛ \ quad k = 0،1،2 ، ...$$

في البسط لدينا $$$F_ {n}$ . في المقام - $$$F_ {n + 1}$ .

كما تعلم

$$

$$\ lim_ {n \ to \ infty} \ frac {F_n} {F_ {n + 1}} = \ frac {1} {\ Phi}$$

$$$\ Phi$ - النسبة الذهبية. عدد غير عقلاني. الآن يمكننا كتابة صيغتنا على النحو التالي:

$$

$$Q_k = \ lfloor \ frac {2k} {\ Phi} \ rfloor \؛ (\ textrm {mod} \؛ 2) ؛ \ quad k = 0،1،2 ، ...$$

لقد حصلنا على صيغة يمكننا من خلالها ملء تسلسل البلياردو بالترتيب ، والذي يساوي عرضه $$$\ Phi$ والطول $$$1$ . طول التسلسل = $$$\ infty$ ، ولكن يمكننا استعادة جزء من النموذج ، والانتقال من اليسار إلى اليمين بالتسلسل والنظر إلى الزاوية اليسرى العليا للبلياردو. يبقى لمعرفة كيفية العد $$$\ Phi$

يمكن إعادة كتابة الوحدة مقسومة على النسبة الذهبية على النحو التالي:

$$

$$\ frac {1} {\ Phi} = \ frac {-1 + {\ sqrt {5}}} {2}$$

يمكننا التخلص من اثنين:

$$

$$\ frac {2k} {\ Phi} = \ frac {2k (-1 + {\ sqrt {5}})} {2} = k \ sqrt {5} -k$$

صيغتنا تأخذ الشكل:

$$

$$Q_k = \ lfloor k \ sqrt {5} -k \ rfloor \؛ (\ textrm {mod} \؛ 2) ؛ \ quad k = 0،1،2 ، ...$$

من أجل الوضوح ، وجهت طاولة. في العمود الثالث ، نتجاهل الجزء الكسري ونترك الكل. في العمود الرابع ، نتحقق من تكافؤ الجزء الصحيح:



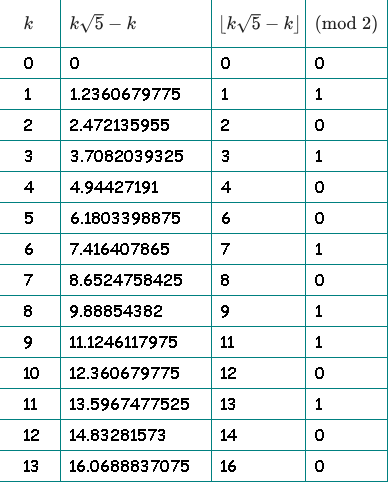
في العمود الرابع حصلنا على تسلسلنا: 01010010110100 ...

نواصل حساب البتات للباقي $$$ك$ . استعادة جزء من نمط البلياردو مع الجانبين $$$1$ و $$$\ Phi$ :



إذا كنت لا تأخذ بعيدا في كل مرة $$$ك$ - ثم يتم قلب كل بت في التسلسل. نحصل على الصيغة العامة:

$$

$$Q_k = \ lfloor k \ sqrt {x} \ rfloor \؛ (\ textrm {mod} \؛ 2) ؛ \ quad k = 0،1،2 ، ...$$

ما الذي يمنعنا من استخدام الجذر التربيعي لثلاثة أو ، على سبيل المثال ، اثنين بدلاً من الجذر التربيعي لخمسة أشخاص؟ لا شيء

نحن نبني تسلسل ل $$$k \ sqrt {3} + k$

 var x=3; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x)+k)%2; 

البتات القليلة الأولى من التسلسل:
00100101101001001011010010110110100101101001001011010010010110100101 ...

سوف نتصور باستخدام رسومات السلاحف. زوايا 90 و -90 درجة. حجم القطعة الأولي هو 5 بكسل:



حجم الجزء الأولي هو 0.5 بكسل:



نحن نبني تسلسل ل $$$k \ sqrt {2}$

 var x=2; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x))%2; 

البتات القليلة الأولى من التسلسل ( A083035 ):
01001101100100110010011011001101100100110110011011001001100100110110 ...

زوايا 90 و -90 درجة. حجم القطعة الأولي هو 5 بكسل:



حجم الجزء الأولي هو 0.5 بكسل:





زوايا 60 و -60 درجة. حجم القطعة الأولي هو 5 بكسل:



السيناريو التصور

شخص ما قد يشك في أن تكافؤ عدد صحيح من $$$k \ sqrt {2}$ يعطي تسلسل كسورية. نحن تصور جزء من هذا التسلسل بالطريقة الثانية:



من أجل الوضوح ، رسمت على أطول منحنى في النموذج الناتج:



هذا المنحنى له اسم - "كلمة فيبوناتشي كسورية".

كيفية الحصول على هذا التسلسل باستخدام البلياردو؟ نأخذ البلياردو ، عرضه = 1 ، والارتفاع = $$$\ sqrt {2}$ . في الحدود العليا والسفلى ، نصلح اتجاه حركة الكرة. إذا تحركت الكرة من اليسار إلى اليمين - اكتب 0 ، وإذا كانت من اليمين إلى اليسار - اكتب 1.



اثنين من الرسوم البيانية:

$$

$$z = \ lfloor y \ sqrt {x} \ rfloor \؛ (\ textrm {mod} \؛ 2)$$

$$

$$z = \ lfloor yx \ sqrt {2} \ rfloor \؛ (\ textrm {mod} \؛ 2)$$

يمكنك الاستمرار في هذا السياق لفترة طويلة جدًا - تتميز الأنماط بالعديد من الخصائص المثيرة للاهتمام. لكن المادة كانت بالفعل مرهقة للغاية. سأقول عن واحدة من الخصائص المثيرة للاهتمام في النهاية.