مقدمة
تم نشر العديد من المقالات [1،2،3] على موقع هبر والتي تتعلق بشكل مباشر أو غير مباشر بهذا الموضوع. في هذا الصدد ، لا يمكن للمرء أن يفشل في ملاحظة المنشور [1] بعنوان "الرياضيات على الأصابع: منظم خطي تربيعي" ، والذي يشرح بشكل شائع مبدأ تشغيل وحدة تحكم LQR المثلى.
أردت أن أستمر في هذا الموضوع ، بعد أن درست التطبيق العملي لطريقة التحسين الديناميكي ، ولكن في مثال ملموس باستخدام Python. أولاً ، بضع كلمات حول المصطلحات وطريقة التحسين الديناميكي.
تنقسم طرق التحسين إلى ساكنة وديناميكية. كائن التحكم في حالة حركة مستمرة تحت تأثير العوامل الخارجية والداخلية المختلفة. لذلك ، يتم إعطاء نتيجة التحكم لعنصر التحكم T ، وهذه هي مهمة التحسين الديناميكي.
باستخدام طرق التحسين الديناميكي ، يتم حل المشكلات المرتبطة بتوزيع الموارد المحدودة على مدى فترة زمنية ، وتتم كتابة الوظيفة الهدف كوظيفة متكاملة.
الجهاز الرياضي لحل مثل هذه المشكلات هو الطرق المختلفة: حساب التفاضل والتكامل الكلاسيكي للتغيرات ، ومبدأ الحد الأقصى L.S. Pontryagin والبرمجة الديناميكية R. Bellman.
يتم إجراء تحليل وتوليف أنظمة التحكم في مساحات الوقت والتردد والحالة. يتم إدخال تحليل وتوليف أنظمة التحكم في فضاء الدولة في المناهج الدراسية ، ومع ذلك ، تم تصميم التقنيات المقدمة في المواد التدريبية باستخدام وحدة تحكم SQR لماتلاب ولا تحتوي على أمثلة عملية للتحليل.
الغرض من هذا المنشور هو النظر في طرق تحليل وتوليف أنظمة التحكم الخطي في فضاء الدولة باستخدام المثال المعروف لتحسين نظام التحكم في محرك كهربائي وطائرة تستخدم لغة برمجة بيثون.
إثبات رياضي لطريقة التحسين الديناميكية
للتحسين ، يتم استخدام معايير السعة (MO) والتماثل (CO) والأمثل الوسطية (KO).
عند حل مشاكل التحسين في فضاء الحالة ، يتم إعطاء نظام ثابت خطي بواسطة معادلات المصفوفة المتجهة:
dotx= fracdxdt=A cdotx+B cdotu؛y=C cdotx، (1)
يتم تعيين معايير متكاملة للحد الأدنى من استهلاك الطاقة التحكم والحد الأقصى للسرعة من قبل وظائف:
Jx= int infty0(xTQx+uTRu+2xTNu)dt rightarrowmin، (2)
Ju= int infty0(yTQy+uTRu+2yTNu)dt rightarrowmin. (3)
قانون التحكم u في شكل ملاحظات خطية على متغيرات الحالة x أو على متغيرات الإخراج y:
u= pmKx،u= pmKyيقلل هذا التحكم من معايير الجودة التربيعية (2) ، (3). في العلاقات (1) ÷ (3) ، Q و R هي مصفوفات محددة إيجابية متماثلة للأبعاد [n × n] و [m × m] ، على التوالي ؛ K عبارة عن مصفوفة لمعاملات ثابتة للأبعاد [m × n] ، وقيمها غير محدودة. إذا تم حذف معلمة الإدخال N ، فسيتم اعتبارها صفرًا.
يتم تحديد حل هذه المشكلة ، والتي تسمى مشكلة التحسين التربيعي (LQR- التكامل) الخطي ، في فضاء الحالة بالتعبير:
u=R−1BTPxحيث يجب أن تفي المصفوفة P بمعادلة Ricatti:
ATP+PA+PBR−1BTP+Q=0المعايير (2) ، (3) متناقضة أيضًا ، نظرًا لأن تنفيذ المصطلح الأول يتطلب مصدرًا للطاقة العالية بلا حدود ، وللمصدر الثاني ، مصدر طاقة منخفضة بشكل غير محدود. يمكن تفسير ذلك بالتعبير التالي:
Jx= int infty0xTQxdt ،
وهذا هو المعيار

المتجه x ، أي مقياس لتذبذبها في عملية التنظيم ، وبالتالي ، يأخذ قيمًا أصغر في العابرين سريعة التقلص مع أقل ، والتعبير:
Ju= int infty0uTRudtهو مقياس لكمية الطاقة المستخدمة للتحكم ؛ إنه عقوبة لتكاليف الطاقة في النظام.
تحدد مصفوفات الوزن Q و R و N قيود الإحداثيات المقابلة. إذا كان أي عنصر من هذه المصفوفات مساوياً للصفر ، فإن الإحداثي المقابل ليس له قيود. في الممارسة العملية ، يتم اختيار قيم المصفوفات Q ، R ، N من خلال طريقة تقديرات الخبراء ، والتجارب ، والأخطاء ، ويعتمد على خبرة ومعرفة مهندس التصميم.
لحل هذه المشكلات ، تم استخدام عوامل تشغيل MATLAB التالية:
تبدأbmatrixR،S،E endbmatrix=lqr(A،B،Q،R،N) و
تبدأbmatrixR،S،E endbmatrix=lqry(Ps،Q،R،N) التي تقلل الوظائف (2) ، (3) بواسطة متجه الحالة x أو بواسطة متجه الإخراج y.
نموذج كائن الإدارة
Ps=ss(A،B،C،D). نتيجة الحساب هي المصفوفة K للتغذية المرتدة المثلى فيما يتعلق بمتغيرات الحالة x ، وحل معادلة Ricatti S و eigenvalues E = eiq (A-BK) لنظام التحكم في الحلقة المغلقة.
المكونات الوظيفية:
Jx=x0TP1x0،Ju=x0TP2x0حيث x0 هي ناقل الحالات الأولية ؛
P1 و
P2 - المصفوفات غير المعروفة التي هي حل لمعادلات المصفوفة Lyapunov. تم العثور عليها باستخدام وظائف.
P1=lyap(NN،Q) و
P2=lyap(NN،KTRK) ،
NN=(A+BK)Tميزات تنفيذ طريقة التحسين الديناميكية باستخدام Python
على الرغم من أن مكتبة أنظمة التحكم Python [4] لها وظائف: control.lqr ، control.lyap ، لا يمكن استخدام control.lqr إلا إذا تم تثبيت وحدة slycot ، وهي مشكلة [5]. عند استخدام دالة lyap في سياق المهمة ، ينتج عن التحسين عنصر تحكم. استثناء.تحكم في: يجب أن يكون Q خطأ في مصفوفة متماثل [6].
لذلك ، لتطبيق الدالتين lqr () و lyap () ، استخدمت scipy.linalg:
from numpy import* from scipy.linalg import* def lqr(A,B,Q,R): S =matrix(solve_continuous_are(A, B, Q, R)) K = matrix(inv(R)*(BT*S)) E= eig(AB*K)[0] return K, S, E P1=solve_lyapunov(NN,Ct*Q*C)
بالمناسبة ، يجب أن لا تتخلى عن السيطرة تمامًا ، حيث أن الدالات ((القطب ،) ، ss () ، tf () ، الملاحظات () ، acker () ، المكان () وغيرها تعمل بشكل جيد.
مثال على تحسين LQR في محرك كهربائي
(مثال مأخوذ من المنشور [7])النظر في تركيب وحدة تحكم خطية من الدرجة الثانية التي تلبي المعيار (2) لكائن التحكم المحدد في الفضاء الدولة من خلال المصفوفات:
A = \ تبدأ {bmatrix} & -100 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 \\ & 0 & 1.046 & 0 \ end {bmatrix}؛ B = \ start {bmatrix} 2300 \\ 0 \\ 0 \\\ end {bmatrix}؛ C = \ تبدأ {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}؛ D = 0
A = \ تبدأ {bmatrix} & -100 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 \\ & 0 & 1.046 & 0 \ end {bmatrix}؛ B = \ start {bmatrix} 2300 \\ 0 \\ 0 \\\ end {bmatrix}؛ C = \ تبدأ {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}؛ D = 0
فيما يلي متغيرات الحالة:
x1 - محول الجهد ، الخامس ؛
x2 - المحرك الحالي ، A ؛
x3 - السرعة الزاوية
c−1 . هذا هو نظام TP - DPT مع HB: engine R nom = 30 kW؛ أونوم = 220 فولت ؛ Inom = 147 A ؛؛
omegaω 0 = 169
c−1 ؛
omegaω الحد الأقصى = 187
c−1 ؛ لحظة المقاومة الاسمية Mnom = 150 N * m ؛ تعدد بدء التشغيل = 2 ؛ محول الثايرستور: Unom = 230 V ؛ Uy = 10 B ؛ Inom = 300 ألف ؛ تعدد التيار الزائد لفترة قصيرة = 1.2.
عند حل المشكلة ، نحن نقبل المصفوفة Q قطري. نتيجة للنمذجة ، وجد أن القيم الدنيا لعناصر المصفوفة R = 84 ، و
Q=[[0.01،0،0]،[0،0.01،0]،[0،0،0.01]]. في هذه الحالة ، تتم ملاحظة عملية انتقال رتابة للسرعة الزاوية للمحرك (الشكل 1). في R = 840
Q=[[0.01،0،0]،[0،0.01،0]،[0،0،0.01]] عملية عابرة (الشكل 2) يلبي معيار MO. تم إجراء حساب المصفوفات P1 و P2 عند x0 = [220 147 162].
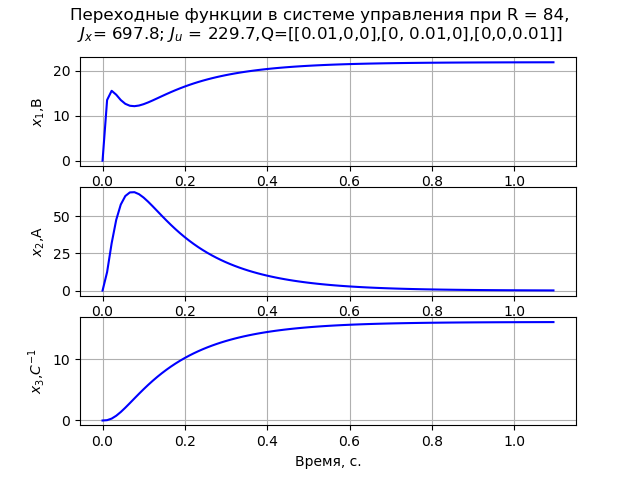 شكل 1
شكل 1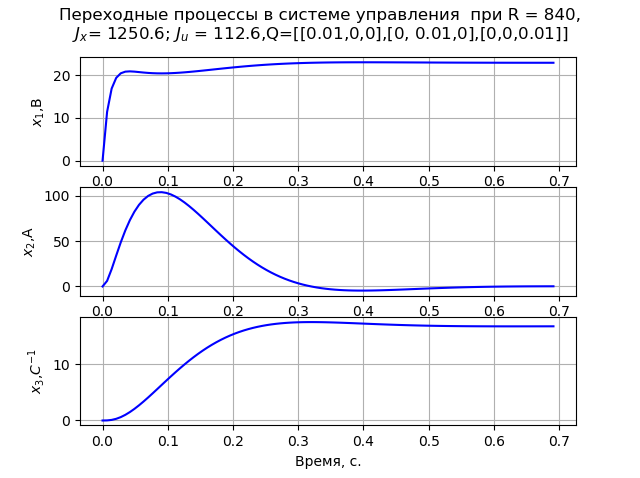 شكل 2
شكل 2بالاختيار المناسب للمصفوفات R و Q ، يمكن تقليل تيار بدء المحرك إلى قيم مقبولة تساوي (2-5) في (الشكل 3). على سبيل المثال ، مع R = 840 و
Q = ([[[0.01،0،0]] ، [0،0.88،0] ، [0،0،0.01]] ، قيمته هي 292 ألف ، ووقت عملية الانتقال في ظل هذه الظروف هو 1.57 ثانية.

الشكل 3
في جميع الحالات التي تم النظر فيها ، تكون التغذية المرتدة على الجهد والتيار سلبية ، وعلى السرعة ، إيجابية ، وهو أمر غير مرغوب فيه وفقًا لمتطلبات الاستقرار. بالإضافة إلى ذلك ، فإن النظام المركب هو ثابت للمهمة وثابت للحمل. لذلك ، فإننا نعتبر تركيب وحدة تحكم PI في مساحة الدولة مع متغير حالة إضافي
x4 - معامل النقل للتكامل.
نحن نمثل المعلومات الأولية في شكل مصفوفات:
A = \ تبدأ {bmatrix} & -100 & 0 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 & 0 \\ & 0 & 1.046 & 0 & 0 \\ & 0 & 0 & 1 & 0 \ end {bmatrix}؛ B = \ تبدأ {bmatrix} 2300 \\ 0 \\ 0 \\ 0 \\\ end {bmatrix} ؛ C = eye (4)) ؛ D = 0A = \ تبدأ {bmatrix} & -100 & 0 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 & 0 \\ & 0 & 1.046 & 0 & 0 \\ & 0 & 0 & 1 & 0 \ end {bmatrix}؛ B = \ تبدأ {bmatrix} 2300 \\ 0 \\ 0 \\ 0 \\\ end {bmatrix} ؛ C = eye (4)) ؛ D = 0تم الحصول على العابرين للمهام المطابقة لمعيار MO عند R = 100 و q11 = q22 = q33 = 0.001 و q44 = 200. ويبين الشكل 4 متغيرات الحالة العابرة التي تؤكد على النجم الفلكي للنظام حسب المهمة والحمل.
قائمة البرنامج (الشكل 4). 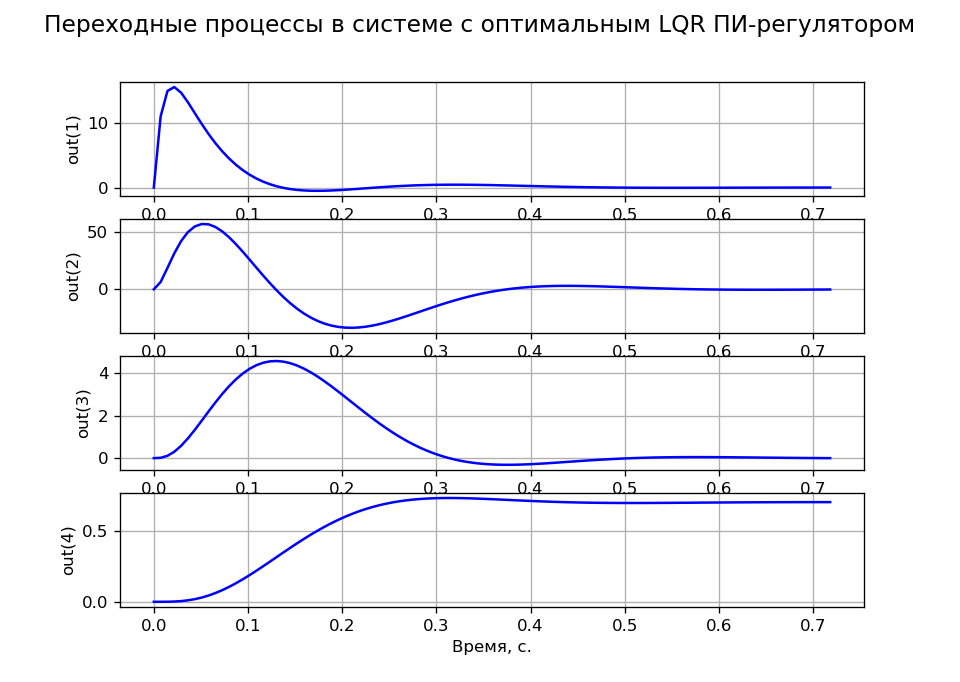 شكل 4
شكل 4لتحديد المصفوفة K ، تحتوي مكتبة أنظمة التحكم Python على وظيفتين K = acker (A، B، s) و K = place (A، B، s) ، حيث s هي المتجه - صف الأقطاب المطلوبة لوظيفة النقل في نظام التحكم في الحلقة المغلقة. لا يمكن استخدام الأمر الأول إلا للأنظمة ذات الإدخال الواحد في u لـ n≤5. لا يحتوي الثاني على مثل هذه القيود ، ولكن يجب ألا يتجاوز تعدد الأعمدة رتبة المصفوفة B. ويظهر مثال على استخدام عامل التشغيل acker () في القائمة وفي (الشكل 5).
قائمة البرنامج (الشكل 5).  شكل 5
شكل 5الخاتمة
إن تنفيذ LQR - تحسين محرك كهربائي الواردة في المنشور ، مع الأخذ في الاعتبار استخدام وظائف جديدة lqr () و lyap () ، سوف يسمح لنا بالتخلي عن استخدام برنامج MATLAB المرخص عند دراسة القسم المقابل من نظرية التحكم.
مثال على تحسين LQR في طائرة (LA)
(مثال مأخوذ من منشور Astrom و Mruray ، الفصل 5 [8] ووضعه في صيغته النهائية من قبل مؤلف المقال من حيث استبدال وظيفة lqr () وتقليل المصطلحات إلى المصطلح المقبول عمومًا)الجزء النظري ، نظرية موجزة ، تم بالفعل النظر في تحسين LQR أعلاه ، لذلك دعونا ننتقل إلى تحليل الشفرة مع التعليقات المقابلة:
المكتبات المطلوبة ووظيفة التحكم LQR. from scipy.linalg import*
الشروط الأولية والمصفوفات الأساسية A ، B ، C ، D النماذج. xe = [0, 0, 0, 0, 0, 0];
نحن نبني المدخلات والمخرجات المقابلة للتغيرات خطوة بخطوة في موقف س ص. تتوافق المتجهات xd و yd مع الحالة الثابتة المطلوبة في النظام. المصفوفات Cx و Cy هما المخرجات المقابلة للنموذج. لوصف ديناميات النظام ، نستخدم نظامًا لمعادلات مصفوفة المتجهات:
\ left \ {\ start {matrix} xdot = Ax + Bu => xdot = (A-BK) x + xd \\ u = -K (x-xd) \\ y = Cx \\ \ end {matrix} \ صحيح.
\ left \ {\ start {matrix} xdot = Ax + Bu => xdot = (A-BK) x + xd \\ u = -K (x-xd) \\ y = Cx \\ \ end {matrix} \ صحيح.
يمكن نمذجة ديناميات حلقة مغلقة باستخدام دالة step () ، بالنسبة إلى K \ cdot xd و K \ cdot xd كمتجهات إدخال ، حيث:
xd = matrix([[1], [0], [0], [0], [0], [0]]); yd = matrix([[0], [1], [0], [0], [0], [0]]);
تدعم مكتبة التحكم الحالية 0.8.1 جزءًا فقط من وظائف SISO Matlab لإنشاء وحدات تحكم للتغذية المرتدة ، لذلك ، من الضروري قراءة البيانات من وحدة التحكم ، لذلك من الضروري إنشاء متجهات الفهرس lat () و alt () للديناميكية -x والرأسي -y الديناميكية.
lat = (0,2,3,5); alt = (1,4);
يتم عرض الرسوم البيانية بالتتابع ، واحدة لكل مهمة.
figure(); title(" x y") plot(Tx.T, Yx.T, '-', Ty.T, Yy.T, '--'); plot([0, 10], [1, 1], 'k-'); axis([0, 10, -0.1, 1.4]); ylabel(' '); xlabel(''); legend(('x', 'y'), loc='lower right'); grid() show()
الرسم البياني: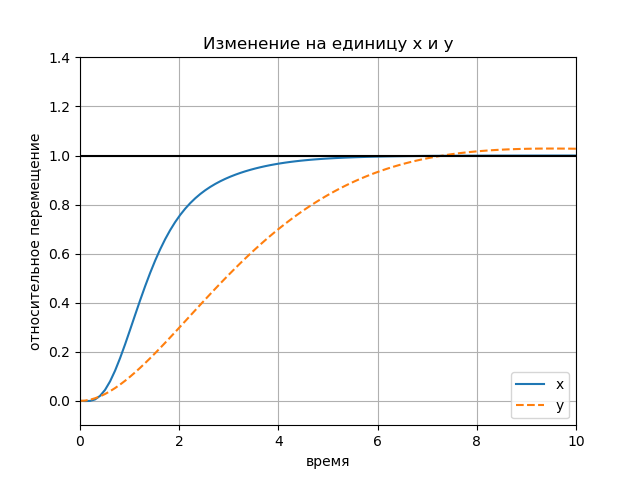
تأثير السعة من الإجراءات المدخلات الرسم البياني: الرسم البياني:
الرسم البياني: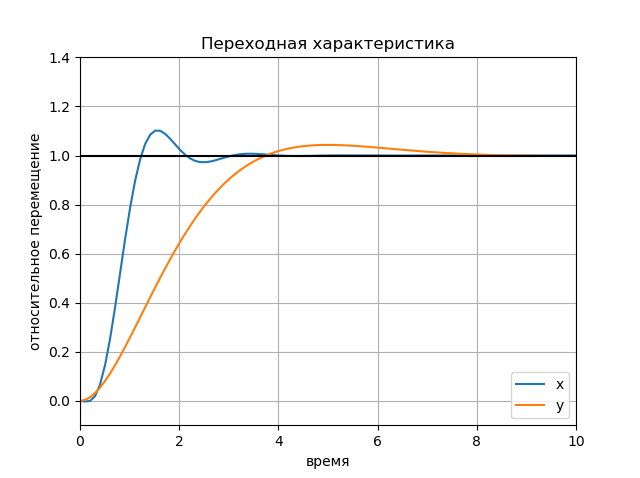 الرسم البياني:
الرسم البياني: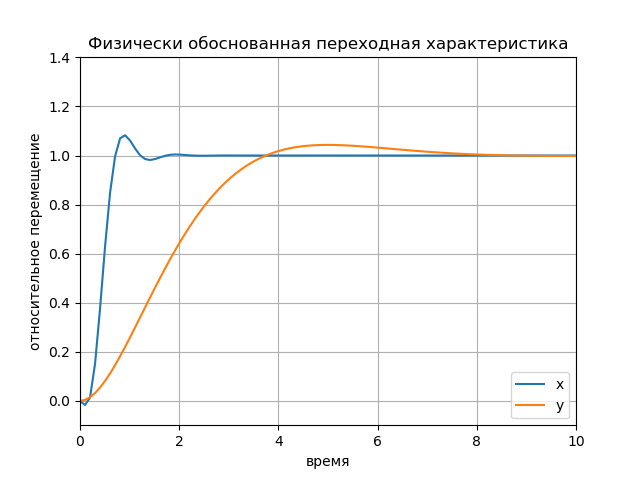
الخلاصة:
سيسمح لنا تنفيذ تحسين LQR في الطائرة المقدمة في المنشور ، مع الأخذ في الاعتبار استخدام وظيفة lqr () الجديدة ، بالتخلي عن استخدام برنامج MATLAB المرخص عند دراسة القسم المقابل من نظرية التحكم.
المراجع
1.
الرياضيات على الأصابع: تحكم خطي من الدرجة الثانية.2.
مساحة الدولة في مشاكل تصميم أنظمة التحكم المثلى.3.
استخدام مكتبة أنظمة التحكم Python لتصميم أنظمة التحكم الآلي.4.
مكتبة أنظمة التحكم بايثون.5.
Python - لا يمكن استيراد وحدة slycot إلى spyder (RuntimeError & ImportError).6.
مكتبة أنظمة التحكم بايثون.7.
معايير للتحكم الأمثل و lqr الأمثل في محرك كهربائي.