كيف يساعد لغز الأطفال على كشف أسرار المغناطيسية

كانت المغناطيسات مألوفة لدى الناس منذ العصور القديمة ، لكن فيزياء المغناطيسية المغناطيسية لا تزال لغزا. الآن اللغز المألوف يجعل الفيزيائيين أقرب إلى الإجابة على الأسئلة

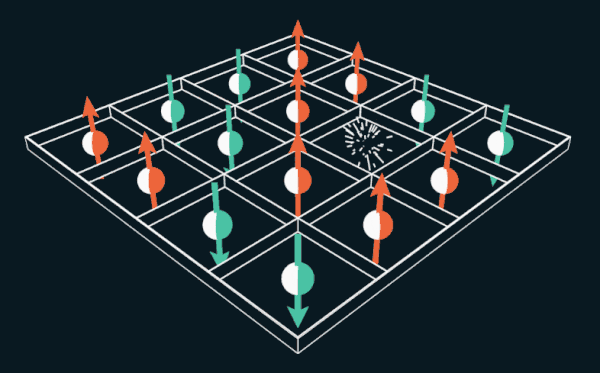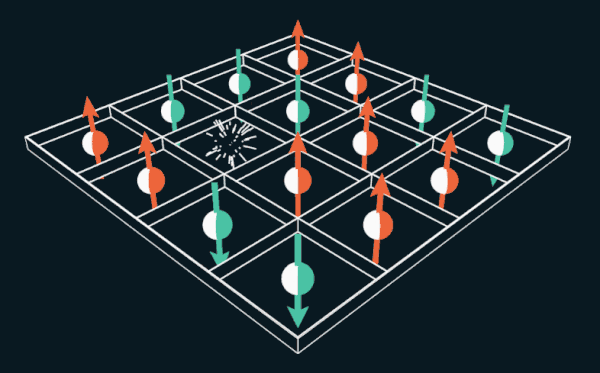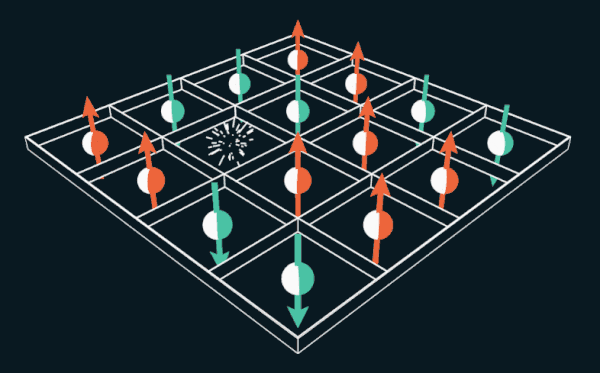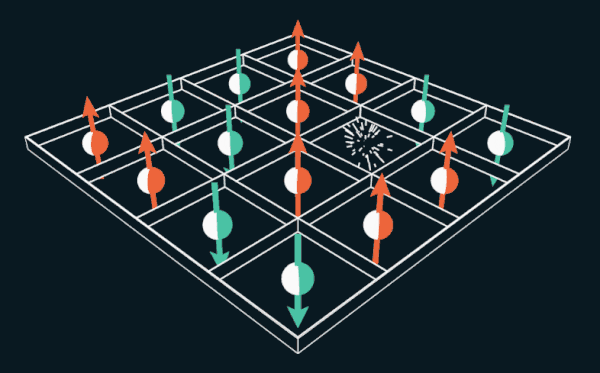توفر لعبة 15 للاعب تحريك بلاطات مرقمة داخل الشبكة. إذا قمت باستبدال الأرقام بنُسخ الإلكترونات ، فيمكن استخدام اللغز لشرح كيفية عمل المغناطيس الدائم.

لعدة أشهر في عام 1880 ، استسلمت مناطق كاملة من الولايات المتحدة للإدمان ، نظائرها التي لم يرها أحد من قبل. وكتبت مجلة ويكلي نيوز- ديموقراطية في إمبيريا ، كانساس ، 12 مارس / آذار 1880: "لقد تفشي وباء حرفيًا في جميع أنحاء البلاد." المدن بأكملها مغرية ، الناس يفقدون النوم ويصبحون مجانين. " انتشر الوباء إلى أوروبا ، وحتى وصل إلى أستراليا مع نيوزيلندا.

لقد أصبح المرض شغفًا جديدًا: تثبيط لعبة الألغاز الميكانيكية البسيطة "15". ما زال معروفًا ، ويتكون من حقل 4 × 4 مربّع يمكنك من خلاله نقل 15 بلاطة ترقيمًا لترتيبها بالترتيب.

وفقًا لمعايير اليوم ، تبدو اللعبة قديمة ، لكن في عام 1880 كانت في ذروة الشعبية. وكتبت الصحيفة "لا يمكن لأي طفل أن يقاوم مثل هذا الترفيه ، فلن يكون أي شخص بالغ قويًا أو متعجرفًا للهروب من سحرها". وربما نشأت خيبة الأمل من حقيقة مثبتة رياضيا وهي أن نصف تكوينات هذا اللغز فقط يمكن حلها بنجاح (والتي ربما لم تكن معروفة لأولئك الذين تعرضوا لتأثيرها).

اليوم ، أي بعد 140 عامًا تقريبًا ، إحياء الاهتمام باللعبة "15" مرة أخرى ، لكن هذه المرة لا تعمل كإلهاء ، ولكن كوسيلة لفهم لغز يبدو غير ذي صلة وأكثر تعقيدًا: كيفية عمل المغناطيس.

المغناطيس الدائم ، مثل تلك التي تعلق على باب الثلاجة ، تنجذب لظاهرة مثل المغناطيسية المغناطيسية . في مغناطيس الحديد ، يتم محاذاة يدور الإلكترونات ، وأنها تولد معا المجال المغناطيسي. بتعبير أدق ، تعرض المعادن مثل الحديد والكوبالت والنيكل مغنطيسية الفرقة ، لأن إلكتروناتها قادرة على التحرك بحرية داخل المادة. كل إلكترون لديه لحظة مغناطيسية خاصة به ، ولكن من أجل فهم كيف ولماذا تصطف كل هذه اللحظات في المغناطيس ، من الضروري حساب التفاعلات الكمومية بين جميع الإلكترونات ، وهو أمر صعب للغاية.

وقال واي لي ، عالم الفيزياء بجامعة جونز هوبكنز: "تعد المغناطيسية في المنطقة واحدة من أكبر التحديات في فيزياء المواد النظرية المختصرة".

ومع ذلك ، ربما يكون لي وطالبان من الخريجين ، إريك بوبروف وكيتون ستيوبس ، قد اقتربا قليلاً من حل هذه المشكلة. باستخدام لغز الرياضيات "15" ، وسعوا النظرية المشهورة التي تصف الحالة المثالية للمغناطيسية في المنطقة. في تحليلهم الجديد ، الذي نشر في دورية Physical Review B ، قاموا بتوسيع نطاق النظرية لشرح نظام أوسع وأكثر واقعية ، مما قد يؤدي إلى نموذج أكثر دقة للمغناطيس.

قال دانييل أروفاس ، عالم فيزياء بجامعة كاليفورنيا ، سان دييغو: "إنها وظيفة رائعة". "يعجبني هذا العمل بشكل خاص نظرًا لوجود عدد قليل جدًا من النتائج التفصيلية فيما يتعلق بمغناطيس المنطقة وأنها مجزأة جدًا."

ثقب القفز

على المستوى الأساسي ، يجب أن تطيع الإلكترونات الموجودة في المعدن قيدين رئيسيين. أولاً ، إنهم جميعهم مشحونون سلبًا ، وبالتالي يصدون بعضهم البعض. ثانياً ، الإلكترونات مطلوبة لإطاعة ما يسمى مبدأ باولي ، الذي يفترض أن اثنين من الجسيمات [مع نصف عدد صحيح تدور / تقريبا. trans.] لا يمكن أن يكون في نفس الحالة الكمية. وهذا يعني أن الإلكترونات التي لها نفس الدوران - بما يتناسب مع اللحظة المغناطيسية للإلكترون - لا يمكنها شغل نفس الحالة في ذرة المعدن. ويمكن أن اثنين من الإلكترونات مع يدور المعاكس.

اتضح أن أبسط طريقة لتلبية كل من التنافر المتبادل والقيود المفروضة على مبدأ باولي لمجموعة من الإلكترونات ستكون منفصلة ومحاذاة يدور - ونتيجة لذلك تصبح المادة المغناطيسية.

ومع ذلك ، هذه ليست سوى صورة مبسطة. لم يستطع الفيزيائيون بناء نموذج مفصل لظهور مثل هذا النمط المنظم للدوران المحاذاة من تفاعلات كمية لا حصر لها بين الإلكترونات الفردية. على سبيل المثال ، كما أوضح لي ، يمكن الخلط بين وظيفة الموجة للإلكترون - وصف رياضي معقد لخصائصها الكمومية - مع دالة الموجة لإلكترون آخر. لفهم تمامًا كيف يؤدي سلوك الجسيمات الفردية إلى ظهور ظاهرة جماعية مثل المغناطيسية المغناطيسية ، سيتعين عليك مراقبة وظيفة الموجة لكل إلكترون في النظام ، بينما يغير باستمرار وظيفة الموجة لكل من الإلكترونات المتبقية في عملية تفاعلها. في الممارسة العملية ، فإن هذا التشابك المنتشر يجعل من المستحيل تدوين المعادلات الكاملة والشاملة اللازمة لوصف المغناطيسية المغناطيسية.

بدلاً من ذلك ، يحاول الفيزيائيون ، بمن فيهم Lee ، جمع المعلومات من خلال دراسة نماذج مبسطة مثالية تصف الفيزياء الكامنة وراء المغناطيسية المغناطيسية. على وجه الخصوص ، يمتد أحدث أعمالها إلى اكتشاف مهم تحقق منذ أكثر من 50 عامًا.

في منتصف الستينيات من القرن الماضي ، استنتج اثنان من الفيزيائيين من الجانبين المتقابلين من الكرة الأرضية أدلة تثبت بشكل مستقل السبب الذي يجعل الإلكترونات محاذاة وخلق حالة مغناطيسية مغناطيسية. ديفيد توليس ، عالم الفيزياء الذي عمل في جامعة كامبريدج وفاز في النهاية بجائزة نوبل لعام 2016 ، ويوسوكي ناجاوكا ، عالم الفيزياء في جامعة ناغويا الذي كان يزور جامعة كاليفورنيا في سان دييغو في ذلك الوقت ، نشر أدلةهم في عامي 1965 و 1966 ، على التوالي. . تستند نتيجتها ، التي تسمى نظرية Nagaoki-Tules (أو ببساطة نظرية Nagaoki) ، إلى نظام مثالي من الإلكترونات الموجودة على الشبكة الذرية. لذلك ، على الرغم من أنه لا يفسر سلوك المغناطيس الحقيقي ، إلا أنه كان لا يزال مهمًا ، حيث يظهر لأول مرة من حيث المبدأ لماذا يجب أن تتم محاذاة دوران الإلكترون. وبما أن تحليلهم كان دليلًا رياضيًا ، فقد كان دقيقًا ، وليس مثقلًا بتقديرات نموذجية للفيزياء.

لفهم النظرية ، تخيل شبكة مربعة ثنائية الأبعاد. يمكن لكل عقدة أن تضع إلكترونين يدوران معاكسين ، لكن النظرية تشير إلى أن وضع إلكترونين في مكان واحد يتطلب كمية لا حصر لها من الطاقة. يضمن ذلك وجود إلكترون واحد فقط في كل مكان. في هذا التكوين ، يمكن لكل إلكترون توجيه دورانه إما لأعلى أو لأسفل. ليس لديهم المحاذاة ، لذلك لا ينبغي أن يكون مثل هذا النظام المغناطيسية.


واي لي ، عالم فيزياء في جامعة جونز هوبكنز

الآن نزيل إلكترون واحد. نتيجة لذلك ، سيكون هناك مكان شاغر يسمى حفرة. يمكن أن ينزلق الإلكترون المجاور إلى حفرة ، تاركًا وراءه مساحة فارغة جديدة. يمكن أن ينتقل إلكترون آخر إلى مكان جديد فارغ ، تاركًا وراءه ثقبًا آخر. في هذا المثال ، هناك ثقب ، في الواقع ، ينتقل من مكان إلى آخر ، ويتنقل حول الشبكة. وجد ثولس وناغاوكا أنه في هذه الحالة ، عندما تتم إضافة ثقب واحد ، فإن الإلكترونات ستحاذي تلقائيًا. لقد أثبتوا أنها ستكون الدولة ذات الطاقة الأقل ، وهي حالة المغناطيس الحديدي.

يوضح Arovas أنه لكي يدخل النظام في حالة أقل طاقة ، يجب أن تكون الفتحة قادرة على الحركة بحرية دون الإخلال بتكوين يدور الإلكترون - تتطلب هذه العملية طاقة إضافية. ولكن عندما تتحرك حفرة ، يجب أن تتحرك الإلكترونات أيضًا. لكي تتحرك الإلكترونات دون الإخلال بتكوين الدورات ، يجب محاذاتها.

وقال ماساكي أوشيكاوا ، الفيزيائي بجامعة طوكيو: "إن نظرية ناوكا هي واحدة من الأمثلة القليلة التي يمكن أن تثبت رياضيا حالات فردية من المغناطيسية المغناطيسية". "لكن من وجهة نظر الفيزياء ، كل هذا اصطناعي للغاية."

على سبيل المثال ، تتطلب الإلكترونات الكثير من الطاقة للتغلب على تنافرها المتبادل واستقرارها في مكان واحد - ولكن ليس لانهائي ، كما تتطلب النظرية. بالإضافة إلى ذلك ، فإن الصورة التي رسمتها Nagaoka و Tules لا تنطبق إلا على الشبكات البسيطة: شبكات ثنائية الأبعاد تتكون من مربعات أو مثلثات ، أو على شبكات مكعبية ثلاثية الأبعاد. في الطبيعة ، تنشأ المغناطيسية الحديدية في العديد من المعادن مع هياكل من كل نوع.

إذا كانت نظرية Nagaoka-Tules تشرح فعلاً المغناطيسية المغناطيسية ، فينبغي أن تنطبق على جميع الشبكات. قال لي إن الناس افترضوا أنها كذلك. "لكن لم يقدم أحد أدلة حقيقية واضحة". حسنا ، هذا لا يزال.

البلاط مع ظهورهم

في عام 1989 ، قام هال تاساكي ، عالم الفيزياء في جامعة جاكوشوين في اليابان ، بتوسيع نطاق هذه النظرية ليجد أنه سيكون قابلاً للتطبيق طالما أن الشبكة لديها خاصية رياضية مثل الاتصال. خذ الحالة البسيطة لشبكة مربعة مع فتحة متحركة واحدة. إذا ، من خلال تحريك فتحة ، يمكنك إعادة إنتاج أي تكوين من الدورات ، مع الاحتفاظ بعدد الإلكترونات ، مع دوران يدور للأعلى وللأسفل ، فإن حالة الاتصال تكون راضية.

ولكن بصرف النظر عن الشبكات المربعة والمثلثية ، والمكعبات ثلاثية الأبعاد ، لم يكن واضحًا ما إذا كان سيتم ربط الحالة الموصولة في حالات أخرى - وبالتالي ، كيف يمكن تطبيق هذه النظرية على نطاق واسع.

للتعامل مع هذه المشكلة ، بدأ Lee بشبكة قرصية سداسية. أدرك طلابها ، Bobrov و Stubis ، في هذه المهمة ، أنها تشبه هوس القرن التاسع عشر: اللغز "15". قم بتبديل الملصقات من الأرقام إلى النهايات ، للأعلى والأسفل ، ويصبح اللغز مكافئًا للمغناطيس الحديدي Nagaoki ، مع وجود ثقب يتحرك على طول شبكة الإلكترون.

يتم السماح للغز عندما تتاح لك الفرصة لإعادة توزيع البلاط في أي تسلسل ، والذي يتزامن تمامًا مع حالة الاتصال. وبالتالي فإن مسألة ما إذا كانت حالة الاتصال متصلة بشبكة معينة تصبح مسألة ما إذا كان من الممكن حل لغز مكافئ على شبكة من هذا الهيكل.

اتضح أنه في عام 1974 قام عالم الرياضيات ريتشارد ويلسون ، الذي يعمل الآن في معهد كاليفورنيا للتكنولوجيا ، بحل هذه المشكلة من خلال تلخيص وحل اللغز "15" لجميع الشبكات. كجزء من الإثبات ، أظهر أنه في جميع المشابك غير المنفصلة تقريبًا (التي تظل كل العقد متصلة حتى بعد إزالة واحدة منها) ، يمكنك نقل البلاط والحصول على أي تكوين ، في حين يظل عدد الحركات متساويًا. الاستثناء الوحيد هو أن المضلعات المفردة أكبر من مثلث ، وشيء يسمى "الرسم البياني ullnull" ، حيث يكون الرأس في وسط المسدس متصلاً برأسيين متعاكسين.

تمكن الباحثون من تطبيق دليل ويلسون بشكل مباشر على نظرية ناجاوكا توليس. لقد أثبتوا أن حالة الاتصال راضية عن نظام من الإلكترونات وفتحة واحدة على جميع المشابك تقريبًا ، بما في ذلك الهياكل الشائعة مثل عسل العسل ثنائي الأبعاد والشبكات ثلاثية الأبعاد على شكل الماس. استثناءان - المضلعات الأكبر من المثلث ، والرسم البياني ullnull - في أي حال ، لا تحدث في المغناطيسية الحقيقية.

انفجار ثقب

قال سريرام شاستري ، عالم فيزياء بجامعة كاليفورنيا في سانتا كروز ، إن استخدام لغز "15" يعد طريقة جديدة ومثمرة. وقال "أحب حقيقة أنه استحدث لغة جديدة ، ومجموعة جديدة من الروابط مع نظرية الرسوم البيانية". "أعتقد أن هذه علاقة غنية - في المستقبل قد تصبح مصدرًا غنيًا للأفكار". ولكن على الرغم من أن الأبحاث تتخذ خطوة مهمة إلى الأمام ، إلا أن المشاكل لا تزال قائمة.

وقال شاستري إن أحد المضاعفات هو أن نظرية Nagaoki-Tules لا تعمل دائمًا عندما تحتاج الفتحة المتحركة إلى اتخاذ عدد فردي من الخطوات أثناء السير على طول الشبكة. ربما تكون المشكلة الأكثر إثارة للدهشة هي أن النظرية تتطلب وجود ثقب واحد بالضبط - لا أكثر ولا أقل. ومع ذلك ، فإن المعادن مليئة بالثقوب ؛ وغالبًا ما تشغل نصف الشبكة.

لكن الفيزيائيين حاولوا تعميم النظرية على الأنظمة ذات الثقوب الكثيرة. باستخدام الطرق العددية ، أوضح الفيزيائيون أن المغناطيسية المغناطيسية Nagaoki تبدو وكأنها تعمل في شبكة مربعة ذات حجم محدود ، تصل إلى 30٪ منها ثقوب. في العمل الحالي ، طبق الباحثون تقنيات تحليلية دقيقة على قرص العسل ثنائي الأبعاد وعلى شبكات ثلاثية الأبعاد على شكل الماس. من الواضح أن المغناطيسية المغناطيسية Nagaoki موجودة ، طالما أن عدد الثقوب لا يتجاوز عدد العقد الشبكية في الدرجة 1/2 للخلايا ، وفي الدرجة 2/5 لشبكة شعرية على شكل الماس.

هذه الحلول الدقيقة يمكن أن تؤدي إلى نموذج أكثر اكتمالا للمغناطيسية في المنطقة. وقال لي: "هذه مجرد خطوة صغيرة واحدة نحو وضع نقطة انطلاق رياضية صارمة للبحث في المستقبل".