المعادلات التفاضلية العصبية العادية
يتم وصف نسبة كبيرة من العمليات من خلال المعادلات التفاضلية ، وهذا قد يكون تطور النظام المادي مع مرور الوقت ، والحالة الطبية للمريض ، والخصائص الأساسية لسوق الأوراق المالية ، وما إلى ذلك. البيانات المتعلقة بهذه العمليات متسقة ومستمرة بطبيعتها ، بمعنى أن الملاحظات هي ببساطة مظاهر لنوع من الحالة المتغيرة باستمرار.
هناك أيضًا نوع آخر من البيانات التسلسلية ، فهو بيانات منفصلة ، على سبيل المثال ، بيانات مهمة NLP. تختلف الحالة في مثل هذه البيانات بشكل منفرد: من حرف أو كلمة إلى أخرى.
الآن تتم معالجة كلا النوعين من هذه البيانات التسلسلية عادة بواسطة شبكات متكررة ، على الرغم من اختلافهما بطبيعتهما ويبدو أنهما يتطلبان أساليب مختلفة.
تم تقديم مقالة مثيرة جدًا للاهتمام في
مؤتمر NIPS الأخير ، والذي يمكن أن يساعد في حل هذه المشكلة. يقترح المؤلفون مقاربة أطلقوا عليها
ODEs العصبية .
حاولت هنا إعادة إنتاج وتلخيص نتائج هذه المقالة من أجل جعل التعرف على فكرتها أسهل قليلاً. يبدو لي أن هذه البنية الجديدة قد تجد مكانًا في الأدوات القياسية لعالم البيانات إلى جانب الشبكات التلافيفية والشبكات المتكررة.
الشكل 1: يتطلب backpropagation التدرج المستمر حل المعادلة التفاضلية زيادة مرة أخرى في الوقت المناسب.
تمثل الأسهم ضبط التدرجات التي تم نشرها للخلف بواسطة التدرجات من الملاحظات.
توضيح من المقال الأصلي.
بيان المشكلة
فليكن هناك عملية تطيع بعض عناصر ODE غير المعروفة وتسمح بوجود عدة ملاحظات (صاخبة) على طول مسار العملية
كيفية العثور على تقريب

وظائف المتكلم

؟
أولاً ، فكر في مهمة أكثر بساطة: لا يوجد سوى ملاحظتان ، في بداية المسار وفي نهايته ،

.
تطور النظام يبدأ من الحالة

في الوقت المحدد

مع بعض الديناميكيات المعلمة تعمل باستخدام أي طريقة لتطور أنظمة ODE. بعد النظام في حالة جديدة

، بالمقارنة مع الدولة

ويتم تقليل الفرق بينهما من خلال تغيير المعلمات

وظائف الديناميات.
أو ، بشكل أكثر رسمية ، فكر في تقليل وظيفة الخسارة

:
لتقليل

، تحتاج إلى حساب التدرجات لجميع المعلمات:

. للقيام بذلك ، تحتاج أولاً إلى تحديد كيف

يعتمد على الدولة في كل لحظة من الزمن

:

يُطلق عليها حالة
متجاورة ، ويتم إعطاء ديناميكياتها بواسطة معادلة تفاضلية أخرى ، والتي يمكن اعتبارها تناظريًا مستمرًا للتمايز بين دالة معقدة (
قاعدة السلسلة ):
يمكن العثور على إخراج هذه الصيغة في ملحق المقالة الأصلية.
يجب اعتبار المتجهات في هذه المقالة ناقلات صغيرة ، على الرغم من أن المقال الأصلي يستخدم كلاً من تمثيل الصف والعمود.حل diffur (4) في الوقت المناسب ، نحصل على الاعتماد على الحالة الأولية

:
لحساب التدرج فيما يتعلق

و

يمكنك ببساطة اعتبارهم جزءًا من الدولة. وتسمى هذه الحالة
زيادة . يتم الحصول على ديناميات هذه الحالة بشكل تافه من الديناميات الأصلية:
ثم الحالة المترافقة لهذه الحالة المعززة:
ديناميات التدرج المعزز:
المعادلة التفاضلية للحالة المتضافرة من الصيغة (4) ثم:
ينتج عن حل ODE هذا في الوقت المحدد:
ما مع
يعطي التدرجات في جميع معلمات الإدخال إلى
ODESolve ODE
حلالا .
يمكن حساب جميع التدرجات (10) ، (11) ، (12) ، (13) معًا في مكالمة واحدة من
ODESolve مع ديناميكيات الحالة المُضافة المدمجة (9).
 توضيح من المقال الأصلي.
توضيح من المقال الأصلي.تصف الخوارزمية أعلاه الانتشار العكسي لتدرج حل ODE للرصدات المتتالية.
في حالة وجود عدة ملاحظات على مسار واحد ، يتم حساب كل شيء بالطريقة نفسها ، ولكن في لحظات الرصد ، يجب ضبط معكوس التدرج المروج بواسطة تدرجات من الملاحظة الحالية ، كما هو مبين في
الشكل 1 .
التنفيذ
الكود أدناه هو عملي في تنفيذ
ODEs العصبية . لقد فعلت ذلك من أجل فهم أفضل لما يحدث. ومع ذلك ، فهو قريب جدًا مما تم تنفيذه في
مستودع مؤلفي المقال. أنه يحتوي على جميع الكود الذي تحتاج إلى فهمه في مكان واحد ، كما أنه تم تعليقه أكثر قليلاً. للتطبيقات والتجارب الحقيقية ، لا يزال من الأفضل استخدام تطبيق مؤلفي المقال الأصلي.
import math import numpy as np from IPython.display import clear_output from tqdm import tqdm_notebook as tqdm import matplotlib as mpl import matplotlib.pyplot as plt %matplotlib inline import seaborn as sns sns.color_palette("bright") import matplotlib as mpl import matplotlib.cm as cm import torch from torch import Tensor from torch import nn from torch.nn import functional as F from torch.autograd import Variable use_cuda = torch.cuda.is_available()
تحتاج أولاً إلى تنفيذ أي طريقة لتطوير أنظمة ODE. من أجل البساطة ، يتم تطبيق طريقة Euler هنا ، على الرغم من أن أي طريقة صريحة أو ضمنية مناسبة.
def ode_solve(z0, t0, t1, f): """ - """ h_max = 0.05 n_steps = math.ceil((abs(t1 - t0)/h_max).max().item()) h = (t1 - t0)/n_steps t = t0 z = z0 for i_step in range(n_steps): z = z + h * f(z, t) t = t + h return z
يصف أيضًا الطبقة الفائقة لوظيفة ديناميكية ذات معلمات مع عدة طرق مفيدة.
أولاً: تحتاج إلى إرجاع جميع المعلمات التي تعتمد عليها الوظيفة في شكل متجه.
ثانياً: من الضروري حساب الديناميات المعززة. تعتمد هذه الديناميات على التدرج اللوني للوظيفة المعلمة من حيث المعلمات وبيانات الإدخال. حتى لا تضطر إلى تسجيل التدرج
اللوني مع كل يد لكل هندسة جديدة ،
سنستخدم طريقة
torch.autograd.grad .
class ODEF(nn.Module): def forward_with_grad(self, z, t, grad_outputs): """Compute f and a df/dz, a df/dp, a df/dt""" batch_size = z.shape[0] out = self.forward(z, t) a = grad_outputs adfdz, adfdt, *adfdp = torch.autograd.grad( (out,), (z, t) + tuple(self.parameters()), grad_outputs=(a), allow_unused=True, retain_graph=True )
يصف الكود أدناه الانتشار
الأمامي والخلفي لمواد ODE العصبية . من الضروري فصل هذا الرمز عن
torch.nn.Module الرئيسي في شكل وظيفة
torch.autograd.Function لأنه في الأخير يمكنك تنفيذ طريقة تعسفية للنشر الخلفي ، على عكس الوحدة النمطية. لذلك هذا مجرد عكاز.
هذه الميزة تكمن وراء نهج
ODE العصبي بأكمله.
class ODEAdjoint(torch.autograd.Function): @staticmethod def forward(ctx, z0, t, flat_parameters, func): assert isinstance(func, ODEF) bs, *z_shape = z0.size() time_len = t.size(0) with torch.no_grad(): z = torch.zeros(time_len, bs, *z_shape).to(z0) z[0] = z0 for i_t in range(time_len - 1): z0 = ode_solve(z0, t[i_t], t[i_t+1], func) z[i_t+1] = z0 ctx.func = func ctx.save_for_backward(t, z.clone(), flat_parameters) return z @staticmethod def backward(ctx, dLdz): """ dLdz shape: time_len, batch_size, *z_shape """ func = ctx.func t, z, flat_parameters = ctx.saved_tensors time_len, bs, *z_shape = z.size() n_dim = np.prod(z_shape) n_params = flat_parameters.size(0)
الآن للراحة ، لف هذه الوظيفة في
nn.Module .
class NeuralODE(nn.Module): def __init__(self, func): super(NeuralODE, self).__init__() assert isinstance(func, ODEF) self.func = func def forward(self, z0, t=Tensor([0., 1.]), return_whole_sequence=False): t = t.to(z0) z = ODEAdjoint.apply(z0, t, self.func.flatten_parameters(), self.func) if return_whole_sequence: return z else: return z[-1]
التطبيق
استعادة وظيفة الديناميات الحقيقية (التحقق من النهج)
كاختبار أساسي ، دعونا الآن نتحقق مما إذا كان بإمكان
Neural ODE استعادة الوظيفة الحقيقية للديناميات باستخدام بيانات الرصد.
للقيام بذلك ، نحدد أولاً وظيفة ديناميات ODE ، ونطور المسار بناءً عليه ، ثم نحاول استعادته من وظيفة الديناميات ذات المعلمات العشوائية.
أولاً ، دعونا نتحقق من أبسط حالات ODE الخطية. وظيفة الديناميات هي ببساطة عمل مصفوفة.
يتم تحديد الوظيفة المدربة بواسطة مصفوفة عشوائية.
علاوة على ذلك ، ديناميات أكثر تعقيدًا بقليل (بدون صورة متحركة ، لأن عملية التعلم ليست جميلة جدًا :))
وظيفة التعلم هنا هي شبكة متصلة بالكامل بطبقة واحدة مخفية.
كود class LinearODEF(ODEF): def __init__(self, W): super(LinearODEF, self).__init__() self.lin = nn.Linear(2, 2, bias=False) self.lin.weight = nn.Parameter(W) def forward(self, x, t): return self.lin(x)
وظيفة الديناميات هي مجرد مصفوفة
class SpiralFunctionExample(LinearODEF): def __init__(self): matrix = Tensor([[-0.1, -1.], [1., -0.1]]) super(SpiralFunctionExample, self).__init__(matrix)
مصفوفة معلمة عشوائيا
class RandomLinearODEF(LinearODEF): def __init__(self): super(RandomLinearODEF, self).__init__(torch.randn(2, 2)/2.)
ديناميات لمسارات أكثر تطورا
class TestODEF(ODEF): def __init__(self, A, B, x0): super(TestODEF, self).__init__() self.A = nn.Linear(2, 2, bias=False) self.A.weight = nn.Parameter(A) self.B = nn.Linear(2, 2, bias=False) self.B.weight = nn.Parameter(B) self.x0 = nn.Parameter(x0) def forward(self, x, t): xTx0 = torch.sum(x*self.x0, dim=1) dxdt = torch.sigmoid(xTx0) * self.A(x - self.x0) + torch.sigmoid(-xTx0) * self.B(x + self.x0) return dxdt
ديناميات التعلم في شكل شبكة متصلة بالكامل
class NNODEF(ODEF): def __init__(self, in_dim, hid_dim, time_invariant=False): super(NNODEF, self).__init__() self.time_invariant = time_invariant if time_invariant: self.lin1 = nn.Linear(in_dim, hid_dim) else: self.lin1 = nn.Linear(in_dim+1, hid_dim) self.lin2 = nn.Linear(hid_dim, hid_dim) self.lin3 = nn.Linear(hid_dim, in_dim) self.elu = nn.ELU(inplace=True) def forward(self, x, t): if not self.time_invariant: x = torch.cat((x, t), dim=-1) h = self.elu(self.lin1(x)) h = self.elu(self.lin2(h)) out = self.lin3(h) return out def to_np(x): return x.detach().cpu().numpy() def plot_trajectories(obs=None, times=None, trajs=None, save=None, figsize=(16, 8)): plt.figure(figsize=figsize) if obs is not None: if times is None: times = [None] * len(obs) for o, t in zip(obs, times): o, t = to_np(o), to_np(t) for b_i in range(o.shape[1]): plt.scatter(o[:, b_i, 0], o[:, b_i, 1], c=t[:, b_i, 0], cmap=cm.plasma) if trajs is not None: for z in trajs: z = to_np(z) plt.plot(z[:, 0, 0], z[:, 0, 1], lw=1.5) if save is not None: plt.savefig(save) plt.show() def conduct_experiment(ode_true, ode_trained, n_steps, name, plot_freq=10):
كما ترون ،
ODE Neural هو جيد جدا في استعادة ديناميات. وهذا هو ، مفهوم ككل أعمال.
تحقق الآن من مشكلة أكثر تعقيدًا (MNIST، haha).
ODE العصبية مستوحاة من ResNets
في ResNet'ax ، تتغير الحالة الكامنة وفقًا للصيغة
اين

هو رقم كتلة و

هذه هي وظيفة تعلمتها الطبقات داخل الكتلة.
في الحد الأقصى ، إذا أخذنا عددًا لا حصر له من الكتل بخطوات أصغر من أي وقت مضى ، فسوف نحصل على ديناميكيات مستمرة للطبقة المخفية في شكل ODE ، تمامًا كما كان أعلاه.
بدءا من طبقة الإدخال

يمكننا تحديد طبقة الإخراج

كحل لهذا ODE في وقت T.
الآن يمكننا الاعتماد

كما المعلمات الموزعة (
المشتركة ) بين جميع الكتل متناهية الصغر.
التحقق من صحة بنية ODE العصبية على MNIST
في هذا الجزء ، سنختبر قدرة
ODE Neural لاستخدامها كمكونات في أبنية مألوفة أكثر.
على وجه الخصوص ، سنستبدل الكتل المتبقية بـ
ODE Neural في مصنف MNIST.
كود def norm(dim): return nn.BatchNorm2d(dim) def conv3x3(in_feats, out_feats, stride=1): return nn.Conv2d(in_feats, out_feats, kernel_size=3, stride=stride, padding=1, bias=False) def add_time(in_tensor, t): bs, c, w, h = in_tensor.shape return torch.cat((in_tensor, t.expand(bs, 1, w, h)), dim=1) class ConvODEF(ODEF): def __init__(self, dim): super(ConvODEF, self).__init__() self.conv1 = conv3x3(dim + 1, dim) self.norm1 = norm(dim) self.conv2 = conv3x3(dim + 1, dim) self.norm2 = norm(dim) def forward(self, x, t): xt = add_time(x, t) h = self.norm1(torch.relu(self.conv1(xt))) ht = add_time(h, t) dxdt = self.norm2(torch.relu(self.conv2(ht))) return dxdt class ContinuousNeuralMNISTClassifier(nn.Module): def __init__(self, ode): super(ContinuousNeuralMNISTClassifier, self).__init__() self.downsampling = nn.Sequential( nn.Conv2d(1, 64, 3, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), ) self.feature = ode self.norm = norm(64) self.avg_pool = nn.AdaptiveAvgPool2d((1, 1)) self.fc = nn.Linear(64, 10) def forward(self, x): x = self.downsampling(x) x = self.feature(x) x = self.norm(x) x = self.avg_pool(x) shape = torch.prod(torch.tensor(x.shape[1:])).item() x = x.view(-1, shape) out = self.fc(x) return out func = ConvODEF(64) ode = NeuralODE(func) model = ContinuousNeuralMNISTClassifier(ode) if use_cuda: model = model.cuda() import torchvision img_std = 0.3081 img_mean = 0.1307 batch_size = 32 train_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=True, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=batch_size, shuffle=True ) test_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=False, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=128, shuffle=True ) optimizer = torch.optim.Adam(model.parameters()) def train(epoch): num_items = 0 train_losses = [] model.train() criterion = nn.CrossEntropyLoss() print(f"Training Epoch {epoch}...") for batch_idx, (data, target) in tqdm(enumerate(train_loader), total=len(train_loader)): if use_cuda: data = data.cuda() target = target.cuda() optimizer.zero_grad() output = model(data) loss = criterion(output, target) loss.backward() optimizer.step() train_losses += [loss.item()] num_items += data.shape[0] print('Train loss: {:.5f}'.format(np.mean(train_losses))) return train_losses def test(): accuracy = 0.0 num_items = 0 model.eval() criterion = nn.CrossEntropyLoss() print(f"Testing...") with torch.no_grad(): for batch_idx, (data, target) in tqdm(enumerate(test_loader), total=len(test_loader)): if use_cuda: data = data.cuda() target = target.cuda() output = model(data) accuracy += torch.sum(torch.argmax(output, dim=1) == target).item() num_items += data.shape[0] accuracy = accuracy * 100 / num_items print("Test Accuracy: {:.3f}%".format(accuracy)) n_epochs = 5 test() train_losses = [] for epoch in range(1, n_epochs + 1): train_losses += train(epoch) test() import pandas as pd plt.figure(figsize=(9, 5)) history = pd.DataFrame({"loss": train_losses}) history["cum_data"] = history.index * batch_size history["smooth_loss"] = history.loss.ewm(halflife=10).mean() history.plot(x="cum_data", y="smooth_loss", figsize=(12, 5), title="train error")
Testing... 100% 79/79 [00:01<00:00, 45.69it/s] Test Accuracy: 9.740% Training Epoch 1... 100% 1875/1875 [01:15<00:00, 24.69it/s] Train loss: 0.20137 Testing... 100% 79/79 [00:01<00:00, 46.64it/s] Test Accuracy: 98.680% Training Epoch 2... 100% 1875/1875 [01:17<00:00, 24.32it/s] Train loss: 0.05059 Testing... 100% 79/79 [00:01<00:00, 46.11it/s] Test Accuracy: 97.760% Training Epoch 3... 100% 1875/1875 [01:16<00:00, 24.63it/s] Train loss: 0.03808 Testing... 100% 79/79 [00:01<00:00, 45.65it/s] Test Accuracy: 99.000% Training Epoch 4... 100% 1875/1875 [01:17<00:00, 24.28it/s] Train loss: 0.02894 Testing... 100% 79/79 [00:01<00:00, 45.42it/s] Test Accuracy: 99.130% Training Epoch 5... 100% 1875/1875 [01:16<00:00, 24.67it/s] Train loss: 0.02424 Testing... 100% 79/79 [00:01<00:00, 45.89it/s] Test Accuracy: 99.170%
بعد تدريب تقريبي للغاية خلال خمس عصور فقط و 6 دقائق من التدريب ، وصل النموذج بالفعل إلى خطأ اختبار أقل من 1٪. يمكننا القول أن
ODEs العصبية تدمج كذلك كعنصر في شبكات أكثر تقليدية.
في مقالتهم ، قارن المؤلفون أيضًا هذا المصنف (ODE-Net) بشبكة منتظمة متصلة بالكامل ، مع ResNet مع بنية مماثلة ، وبنفس البنية الدقيقة ، التي ينتشر فيها التدرج
اللوني مباشرةً من خلال العمليات في
ODESolve (بدون طريقة التدرج المترافق) ( RK-Net).
توضيح من المقال الأصلي.وفقا لهم ، فإن شبكة متصلة بالكامل ذات طبقة واحدة تحتوي على نفس عدد المعلمات تقريبًا مثل
Neural ODE بها خطأ أعلى بكثير في الاختبار ، ResNet مع نفس الخطأ إلى حد كبير به معلمات أكثر بكثير ، و RK-Net بدون طريقة التدرج المترافق يحتوي على خطأ أعلى قليلاً ومع زيادة استهلاك الذاكرة بشكل خطي (كلما كان الخطأ المسموح به
أصغرًا ، زادت الخطوات التي يجب على
ODESolve اتخاذها ، مما يزيد من استهلاك الذاكرة خطيًا بعدد الخطوات).
يستخدم المؤلفون طريقة Runge-Kutta الضمنية مع حجم الخطوة التكيفي في تنفيذها ، على عكس طريقة Euler الأبسط هنا. هم أيضا دراسة بعض خصائص الهندسة المعمارية الجديدة.
ميزة ODE-Net (NFE إلى الأمام - عدد حسابات الوظائف في مسار مباشر)
توضيح من المقال الأصلي.- (أ) تغيير مستوى الخطأ العددي المقبول يغير عدد الخطوات في التوزيع المباشر.
- (ب) الوقت الذي يقضيه التوزيع المباشر يتناسب مع عدد حسابات الوظائف.
- (ج) يمثل عدد العمليات الحسابية لوظيفة الانتشار الخلفي ما يقرب من نصف الانتشار المباشر ، مما يدل على أن طريقة التدرج المتزامن قد تكون أكثر كفاءة من الناحية الحسابية من نشر التدرج اللوني مباشرة من خلال ODESolve .
- (د) عندما يصبح ODE-Net أكثر وأكثر تدريباً ، فإنه يتطلب المزيد والمزيد من العمليات الحسابية للوظيفة (خطوة أصغر من أي وقت مضى) ، وربما التكيف مع التعقيد المتزايد للنموذج.
وظيفة توليدية خفية لنمذجة السلاسل الزمنية
ODE العصبي مناسب لمعالجة البيانات التسلسلية المستمرة حتى عندما يكمن المسار في مساحة مخفية غير معروفة.
في هذا القسم ، سنقوم بتجربة وتغيير توليد تسلسل مستمر باستخدام
Neural ODE ، ونلقي نظرة على المساحة الخفية المستفادة.
يقارن المؤلفون هذا أيضًا بالتسلسلات المتشابهة الناتجة عن الشبكات المتكررة.
تختلف التجربة هنا قليلاً عن المثال المقابل في مستودع المؤلفين ، فهناك مجموعة متنوعة من المسارات.
البيانات
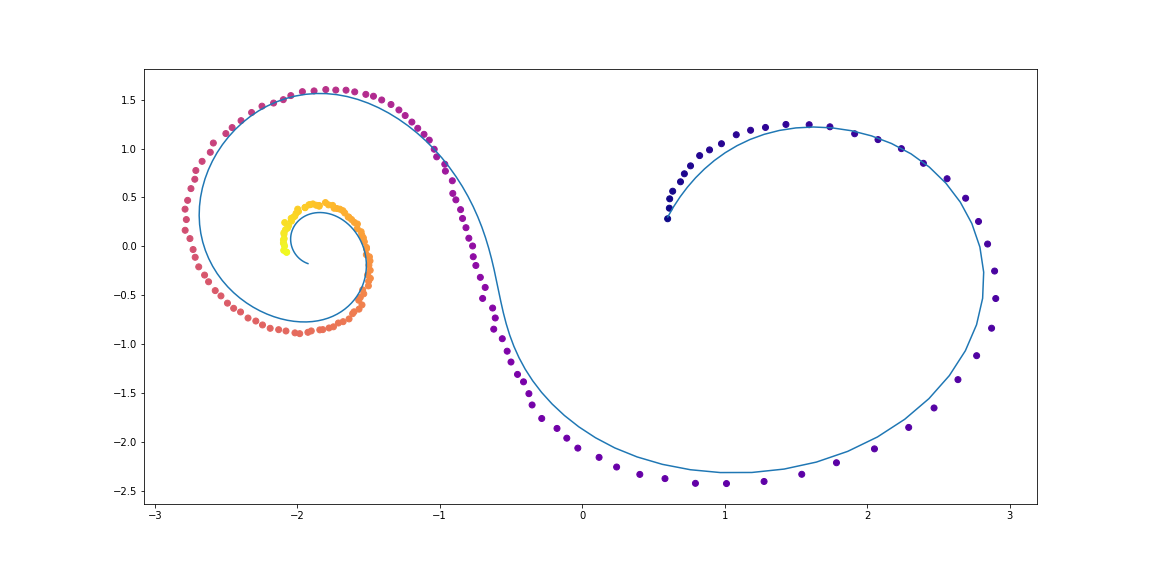
تتكون بيانات التدريب من اللوالب العشوائية ، نصفها في اتجاه عقارب الساعة ، والثاني عكس اتجاه عقارب الساعة. علاوة على ذلك ، يتم أخذ العينات التالية من هذه اللوالب ، التي تتم معالجتها بواسطة نموذج تكرار الترميز في الاتجاه المعاكس ، مما يؤدي إلى بداية حالة مخفية ، والتي تتطور بعد ذلك ، مما يخلق مسارًا في الفضاء الخفي. ثم يتم تعيين هذا المسار كامن إلى مساحة البيانات ومقارنتها مع يليه عينات. وبالتالي ، يتعلم النموذج إنشاء مسارات مشابهة لمجموعة البيانات.
أمثلة من اللوالب مجموعة البياناتVAE كنموذج إنتاجي
نموذج عام من خلال إجراء أخذ العينات:
والتي يمكن تدريبها باستخدام نهج الترميز التلقائي الاختلافات.
- انتقل من خلال التشفير المتكرر من خلال تسلسل الوقت في الوقت المناسب للحصول على المعلمات
 ،
،  التوزيع الخلفي المتغير ، ثم أخذ عينة منه:
التوزيع الخلفي المتغير ، ثم أخذ عينة منه:
- الحصول على المسار الخفي:
- عيّن مسارًا مخفيًا إلى مسار في البيانات باستخدام شبكة عصبية أخرى:

- تعظيم تقييم الحد الأدنى من الصلاحية (ELBO) لمسار العينة:
وفي حالة التوزيع الخلفي الغوسي

ومستوى الضوضاء المعروفة

:
يمكن تمثيل الرسم البياني لحساب نموذج ODE المخفي على النحو التالي
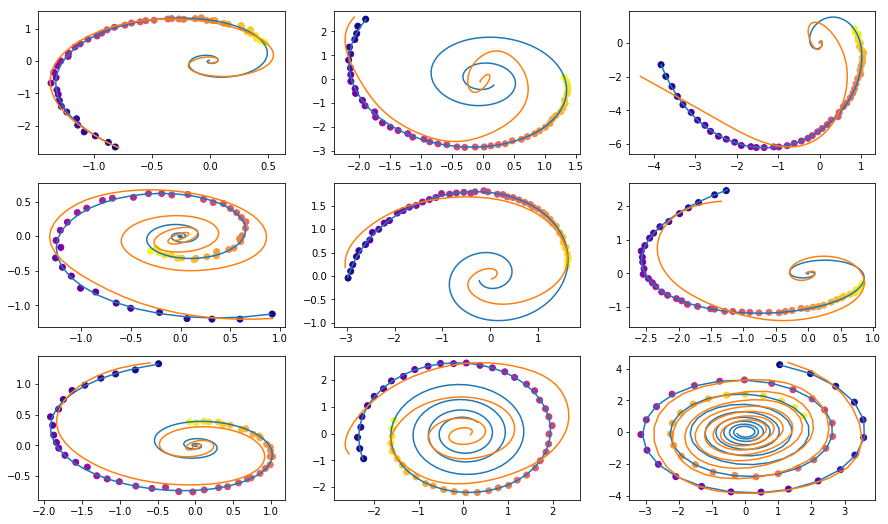
توضيح من المقال الأصلي.يمكن بعد ذلك اختبار هذا النموذج لمعرفة كيفية تقريب المسار باستخدام الملاحظات الأولية فقط.
كودتحديد النماذج
class RNNEncoder(nn.Module): def __init__(self, input_dim, hidden_dim, latent_dim): super(RNNEncoder, self).__init__() self.input_dim = input_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim self.rnn = nn.GRU(input_dim+1, hidden_dim) self.hid2lat = nn.Linear(hidden_dim, 2*latent_dim) def forward(self, x, t):
جيل مجموعة البيانات
t_max = 6.29*5 n_points = 200 noise_std = 0.02 num_spirals = 1000 index_np = np.arange(0, n_points, 1, dtype=np.int) index_np = np.hstack([index_np[:, None]]) times_np = np.linspace(0, t_max, num=n_points) times_np = np.hstack([times_np[:, None]] * num_spirals) times = torch.from_numpy(times_np[:, :, None]).to(torch.float32)
التدريب
vae = ODEVAE(2, 64, 6) vae = vae.cuda() if use_cuda: vae = vae.cuda() optim = torch.optim.Adam(vae.parameters(), betas=(0.9, 0.999), lr=0.001) preload = False n_epochs = 20000 batch_size = 100 plot_traj_idx = 1 plot_traj = orig_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_obs = samp_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_ts = samp_ts[:, plot_traj_idx:plot_traj_idx+1] if use_cuda: plot_traj = plot_traj.cuda() plot_obs = plot_obs.cuda() plot_ts = plot_ts.cuda() if preload: vae.load_state_dict(torch.load("models/vae_spirals.sd")) for epoch_idx in range(n_epochs): losses = [] train_iter = gen_batch(batch_size) for x, t in train_iter: optim.zero_grad() if use_cuda: x, t = x.cuda(), t.cuda() max_len = np.random.choice([30, 50, 100]) permutation = np.random.permutation(t.shape[0]) np.random.shuffle(permutation) permutation = np.sort(permutation[:max_len]) x, t = x[permutation], t[permutation] x_p, z, z_mean, z_log_var = vae(x, t) z_var = torch.exp(z_log_var) kl_loss = -0.5 * torch.sum(1 + z_log_var - z_mean**2 - z_var, -1) loss = 0.5 * ((x-x_p)**2).sum(-1).sum(0) / noise_std**2 + kl_loss loss = torch.mean(loss) loss /= max_len loss.backward() optim.step() losses.append(loss.item()) print(f"Epoch {epoch_idx}") frm, to, to_seed = 0, 200, 50 seed_trajs = samp_trajs[frm:to_seed] ts = samp_ts[frm:to] if use_cuda: seed_trajs = seed_trajs.cuda() ts = ts.cuda() samp_trajs_p = to_np(vae.generate_with_seed(seed_trajs, ts)) fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(15, 9)) axes = axes.flatten() for i, ax in enumerate(axes): ax.scatter(to_np(seed_trajs[:, i, 0]), to_np(seed_trajs[:, i, 1]), c=to_np(ts[frm:to_seed, i, 0]), cmap=cm.plasma) ax.plot(to_np(orig_trajs[frm:to, i, 0]), to_np(orig_trajs[frm:to, i, 1])) ax.plot(samp_trajs_p[:, i, 0], samp_trajs_p[:, i, 1]) plt.show() print(np.mean(losses), np.median(losses)) clear_output(wait=True) spiral_0_idx = 3 spiral_1_idx = 6 homotopy_p = Tensor(np.linspace(0., 1., 10)[:, None]) vae = vae if use_cuda: homotopy_p = homotopy_p.cuda() vae = vae.cuda() spiral_0 = orig_trajs[:, spiral_0_idx:spiral_0_idx+1, :] spiral_1 = orig_trajs[:, spiral_1_idx:spiral_1_idx+1, :] ts_0 = samp_ts[:, spiral_0_idx:spiral_0_idx+1, :] ts_1 = samp_ts[:, spiral_1_idx:spiral_1_idx+1, :] if use_cuda: spiral_0, ts_0 = spiral_0.cuda(), ts_0.cuda() spiral_1, ts_1 = spiral_1.cuda(), ts_1.cuda() z_cw, _ = vae.encoder(spiral_0, ts_0) z_cc, _ = vae.encoder(spiral_1, ts_1) homotopy_z = z_cw * (1 - homotopy_p) + z_cc * homotopy_p t = torch.from_numpy(np.linspace(0, 6*np.pi, 200)) t = t[:, None].expand(200, 10)[:, :, None].cuda() t = t.cuda() if use_cuda else t hom_gen_trajs = vae.decoder(homotopy_z, t) fig, axes = plt.subplots(nrows=2, ncols=5, figsize=(15, 5)) axes = axes.flatten() for i, ax in enumerate(axes): ax.plot(to_np(hom_gen_trajs[:, i, 0]), to_np(hom_gen_trajs[:, i, 1])) plt.show() torch.save(vae.state_dict(), "models/vae_spirals.sd")
— , .
.. . .
, - - .
Neural ODE .
. , , (, ), .
, , .
,
.
, ,
, , , .
:
( ) ( ) ;
-X «» ( ) «» ( ).
bekemax .
Neural ODEs . !