تجميع نقاط الوصول اللاسلكية باستخدام طريقة الوسائل k

يستخدم حاليا التصور وتحليل البيانات على نطاق واسع في صناعة الاتصالات السلكية واللاسلكية. على وجه الخصوص ، يعتمد التحليل اعتمادًا كبيرًا على استخدام البيانات الجغرافية المكانية. ربما يرجع ذلك إلى حقيقة أن شبكات الاتصالات نفسها مشتتة جغرافيا. وفقًا لذلك ، يمكن أن يكون تحليل مثل هذه التشتت ذا قيمة هائلة.

البيانات

لتوضيح خوارزمية التجميع k-mean ، سنستخدم قاعدة البيانات الجغرافية لخدمة WiFi العامة المجانية في نيويورك. مجموعة البيانات متاحة في بيانات مدينة نيويورك المفتوحة. على وجه الخصوص ، يتم استخدام خوارزمية التجميع k-الوسائل لتكوين مجموعات استخدام WiFi استنادًا إلى بيانات خطوط الطول والعرض.

يتم استخراج بيانات خطوط الطول والعرض من مجموعة البيانات نفسها باستخدام لغة البرمجة R:

#1. Prepare data newyork<-read.csv("NYC_Free_Public_WiFi_03292017.csv") attach(newyork) newyorkdf<-data.frame(newyork$LAT,newyork$LON) 

هنا قطعة من البيانات:

نحدد عدد المجموعات

بعد ذلك ، نحدد عدد الكتل التي تستخدم الكود أدناه ، والتي توضح النتيجة في الرسم البياني.

 #2. Determine number of clusters wss <- (nrow(newyorkdf)-1)*sum(apply(newyorkdf,2,var)) for (i in 2:20) wss[i] <- sum(kmeans(newyorkdf, centers=i)$withinss) plot(1:20, wss, type="b", xlab="Number of Clusters", ylab="Within groups sum of squares") 

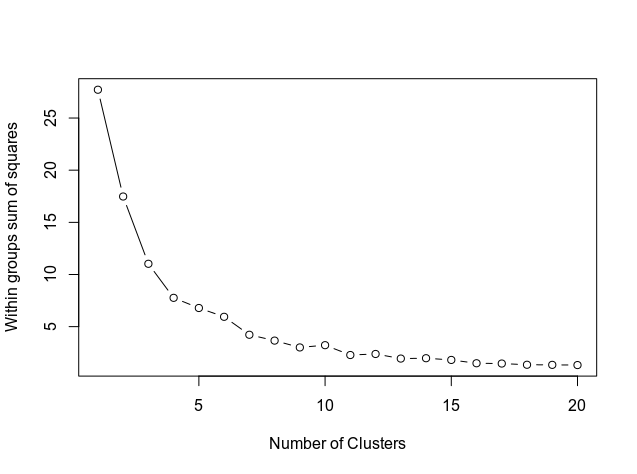
يوضح الرسم البياني كيف يتم محاذاة المنحنى عند حوالي 11. لذلك ، هذا هو عدد الكتل التي سيتم استخدامها في نموذج الوسائل k.

تحليل K- يعني

يتم تحليل الوسائل K:

 #3. K-Means Cluster Analysis set.seed(20) fit <- kmeans(newyorkdf, 11) # 11 cluster solution # get cluster means aggregate(newyorkdf,by=list(fit$cluster),FUN=mean) # append cluster assignment newyorkdf <- data.frame(newyorkdf, fit$cluster) newyorkdf newyorkdf$fit.cluster <- as.factor(newyorkdf$fit.cluster) library(ggplot2) ggplot(newyorkdf, aes(x=newyork.LON, y=newyork.LAT, color = newyorkdf$fit.cluster)) + geom_point() 

تحتوي مجموعة بيانات newyorkdf على معلومات حول خطوط الطول والعرض وتسمية الكتلة:
> newyorkdf
newyork.lat newyork.lon fit.cluster
1 40.75573 -73.94458 1
2 40.75533 -73.94413 1
3 40.75575 -73.94517 1
4 40.75575 -73.94517 1
5 40.75575 -73.94517 1
6 40.75575 -73.94517 1
...
80 40.84832 -73.82075 11

هنا توضيح واضح:



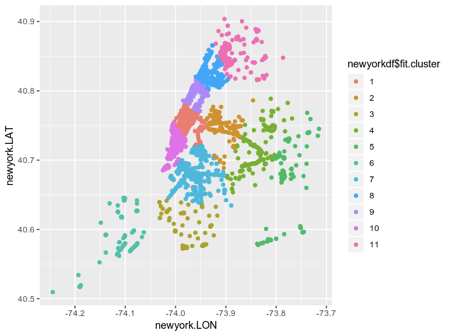
هذا الرسم التوضيحي مفيد ، لكن التصور سيكون أكثر قيمة إذا قمت بتراكبه على خريطة نيويورك نفسها.

 # devtools::install_github("zachcp/nycmaps") library(nycmaps) map(database="nyc") #this should also work with ggplot and ggalt nyc <- map_data("nyc") gg <- ggplot() gg <- gg + geom_map( data=nyc, map=nyc, aes(x=long, y=lat, map_id=region)) gg + geom_point(data = newyorkdf, aes(x = newyork.LON, y = newyork.LAT), colour = newyorkdf$fit.cluster, alpha = .5) + ggtitle("New York Public WiFi") 

يعطي هذا النوع من التجميع فكرة ممتازة عن بنية شبكة WiFi في المدينة. يشير هذا إلى أن المنطقة الجغرافية التي تميزها المجموعة 1 تظهر الكثير من حركة مرور WiFi. من ناحية أخرى ، قد يشير عدد الاتصالات الأقل في المجموعة 6 إلى انخفاض حركة مرور WiFi.

لا تعلمنا التجميعات K-Means لوحدها أن حركة مرور مجموعة معينة مرتفعة أو منخفضة. على سبيل المثال ، عندما يكون للمجموعة 6 كثافة سكانية عالية ، لكن سرعات الإنترنت المنخفضة تؤدي إلى عدد أقل من الاتصالات.

ومع ذلك ، توفر خوارزمية التجميع هذه نقطة انطلاق ممتازة لمزيد من التحليل وتسهل عملية جمع المعلومات الإضافية. على سبيل المثال ، باستخدام هذه الخريطة كمثال ، يمكنك إنشاء فرضيات تتعلق بالمجموعات الجغرافية الفردية. المقال الأصلي هنا .