المهام من الكتاب المدرسي الثاني

الجزء الأول
الجزء الثاني
الجزء الثالث

تتناول هذه المقالة طريقة تقدير نطاق القيم المقبولة وعلاقة هذه الطريقة بالمهام التي تحتوي على وحدة نمطية.

عند حل بعض المشكلات ، من الضروري مراعاة النطاق الذي يمكن أن تكون القيمة المطلوبة فيه.

النظر في طريقة تقدير لحل أوجه عدم المساواة.

لنفترض أن السعر لكل وحدة من السلع يمكن أن يتراوح بين 5 إلى 10 RUB. إعطاء الحد الأعلى يعني تحديد الحد الأقصى للقيمة التي يمكن أن تتخذها الكمية المطلوبة. بالنسبة لوحدتين من البضائع ، السعر الذي لا يتجاوز 10 ، سيكون التقدير العلوي هو 10 + 10 = 20 .

النظر في المشكلة من الملف الشخصي مشكلة الملف MI باشماكوفا
37. تقديرات معروفة للمتغيرات $$$x$ و$$ $ inline $ y: 0 <x <5، 2 <y <3. $ $ inline

إعطاء أعلى علامات التعبيرات التالية:
1. $$$2x + 3y$
2. $$$س س$

5. $$$\ frac {1} {y}$
6. $$$\ frac {x} {y}$

8. $$$س ص$
9. $$$3x-2y$


بشكل عام ، يستخدم تحليل الكميات اللانهائية معيار تقييم. وحدة نمطية (كحي) تجد التطبيق في تعريف الحد.

$$عرض $$ $ \ left | x_ {n} -a \ right | <\ varepsilon $$ عرض $$

النظر في المثال من "مسار التفاضل والتكامل لا يتجزأ" 363 (6)

من السهل تعيين اختلاف الصف

$$

$$\ sum \ frac {1} {\ sqrt {n}} = 1+ \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}} + ...$$

في الواقع ، منذ انخفاض أعضائها ، المبلغ الجزئي التاسع

$$عرض $$ $$ 1+ \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}> n \ cdot \ frac {1} {\ sqrt {n }} = \ sqrt {n} $$ عرض $$

وينمو الإعلان لانهائية مع $$$ن$ .

من أجل إثبات ذلك $$$1+ \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}$ حقا اكثر $$$\ sqrt {n}$ ، تحتاج إلى إجراء تقدير أقل لهذا التعبير. نحصل على نظام عدم المساواة

$$عرض $$ $ \ left \ {\! \ تبدأ {محاذاة} & \ frac {1} {\ sqrt {n-1}}> \ frac {1} {\ sqrt {n}} \\ & \ frac { 1} {\ sqrt {n-2}}> \ frac {1} {\ sqrt {n}} \\ & \ frac {1} {\ sqrt {n-3}}> \ frac {1} {\ sqrt {n}} \\ & ... \ end {محاذاة} \ اليمين. عرض $$ $

بعد إضافة جميع أوجه عدم المساواة في هذا النظام ، نحصل عليها

$$عرض $$ $$ 1+ \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}}> \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + ... + \ frac {1} {\ sqrt {n}} = n \ cdot \ frac {1} {\ sqrt {n}} عرض $$ $

هذا دليل على أن هذه السلسلة تتباعد.

لسلسلة التوافقي ، وهذه الطريقة لا تعمل ، لأن $$$ن$ سلسلة جزئية التوافقي

$$عرض $$ $$ 1+ \ frac {1} {2} + \ frac {1} {3} + ... + \ frac {1} {n}> n \ cdot \ frac {1} {n} = 1 $$ عرض $$

العودة إلى المهمة

38. احسب المبلغ ("المهام للأطفال من 5 إلى 15 سنة")

$$

$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ cdot100}$$

(مع وجود خطأ لا يزيد عن 1٪ من الإجابة)

أعلى تقدير لهذه السلسلة $$$\ frac {n} {n + 1}$ يعطي الرقم 1.

إسقاط المصطلح الأول $$$\ frac {1} {1 \ cdot2}$

(define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 1.0 )(+ n 2.0))) (series_sum_1(- n 1.0))) ) ) ) (writeln (series_sum_1 10)) (writeln (series_sum_1 100)) (writeln (series_sum_1 1000)) (writeln (series_sum_1 10000)) (writeln (series_sum_1 100000)) (writeln (series_sum_1 1000000)) 

نحن نحصل عليها $$$1 - \ frac {1} {1 \ cdot2} = \ frac {1} {2}$
0.4166666666666666363
0.49019607843137253
0.4990019960079833
0.4999000199960005
0.49999000019998724
0.4999990000019941

يمكنك التحقق في ideone.com هنا


إسقاط المصطلحين الأولين $$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3}$

 (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 2.0) (+ n 3.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 1000000) 

سوف نحصل على 0.33333233333632745
المبالغ الجزئية للسلسلة محددة أعلاه.

الصف الإيجابي له دائمًا مبلغ ؛ سيكون هذا المبلغ محددًا (وبالتالي تتقارب السلسلة) إذا كانت المبالغ الجزئية للسلسلة محددة أعلاه ، وغير محدودة (والمتباين متسلسلان) خلاف ذلك.

رمي بعيدا $$$ن$ الشروط الأولية للسلسلة التوافقية.
يثبت (باستخدام الحد الأدنى) ذلك

$$عرض $$ $$ \ frac {1} {n + 1} + \ frac {1} {n + 2} + ... + \ frac {1} {2n}> \ frac {1} {2} $$ عرض $$

إذا تم التخلص من المصطلحين الأولين ، فسيتم تقسيم الأعضاء المتبقين في السلسلة التوافقية إلى مجموعات $$ أعضاء في كل

$$

$$\ frac {1} {3} + \ frac {1} {4}؛ \ frac {1} {5} + \ frac {1} {6} + \ frac {1} {7} + \ frac {1} {8}؛ \ frac {1} {9} + ... \ frac {1} {16}؛ ...؛$$

$$

$$\ frac {1} {2 ^ {k-1} +1} + ... + \ frac {1} {2 ^ {k}}؛ ... ،$$

ثم كل من هذه المبالغ بشكل فردي سيكون أكبر $$$\ frac {1} {2}$ .
... نرى أنه لا يمكن تحديد مبالغ جزئية أعلاه: تحتوي السلسلة على مبلغ غير محدود.

نحسب المبالغ الجزئية التي يتم الحصول عليها عن طريق التخلص منها $$$2 ^ {k}$ شروط.

 #lang racket (* 1.0 (+ 1/3 1/4)) (* 1.0 (+ 1/5 1/6 1/7 1/8)) (* 1.0 (+ 1/9 1/10 1/11 1/12 1/13 1/14 1/15 1/16)) 

نحصل على:
0.583333333333333434
0.6345238095238095
0.6628718503718504
نكتب البرنامج الذي يحسب مجموع سلسلة التوافقي من $$$\ frac {n} {2}$ قبل $$$ن$ اين $$$n = 2 ^ {k}$ في $$$k \ in \ mathbb {N}$

 #lang racket (define (Hn n ) (define half_arg (/ n 2.0)) (define (series_sum n) (if (= n half_arg ) 0 (+ (/ 1.0 n) (series_sum(- n 1)) ) ) ) (series_sum n) ) (Hn 4) (Hn 8) (Hn 16) (Hn 32) 

نحصل على:
0.583333333333333333
0.6345238095238095
0.6628718503718504
0.6777662022075267

يمكنك التحقق في بيئة تطوير متكاملة على الانترنت على الرابط
لمجموعة $$$\ left [1 + 2 ^ {70} ؛ 2 ^ {71} \ right]$ حصلنا على 0.693147 ...
تحقق موجو في ولفرام كلاود هنا .

تؤدي هذه الخوارزمية العودية إلى تجاوز سعة مكدس سريع.
تحتوي هذه المقالة على مثال لحساب المضروب باستخدام خوارزمية تكرارية. نقوم بتعديل هذه الخوارزمية التكرارية بحيث تحسب المبلغ الجزئي Hn داخل حدود معينة ؛ استدعاء هذه الحدود a و b

 (define (Hn ab) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a)) 

الحد الأدنى هو الرقم $$$1 + 2 ^ {k}$ الحد الأعلى هو الرقم $$$2 \ cdot 2 ^ {k}$
نكتب وظيفة تحسب قوة اثنين

 (define (power_of_two k) (define (iteration product counter) (if (> counter k) product (iteration (* product 2) (+ counter 1)))) (iteration 1 1)) 

سنستبدل (+ 1 (power_of_two k)) الحد الأدنى ، ونستخدم الدالة (* 2 (power_of_two k)) أو وظيفتها المكافئة (power_of_two (+ 1 k)) كحد أعلى
أعد كتابة الوظيفة Hn

 (define (Hn k) (define a (+ 1 (power_of_two k)) ) (define b (* 2 (power_of_two k)) ) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a )) 

الآن يمكنك حساب Hn للقيم الكبيرة $$$ك$ .

نكتب في C برنامج يقيس الوقت اللازم لحساب Hn . سوف نستخدم الدالة clock () من <time.h> المكتبة القياسية
يوجد مقال حول قياس وقت المعالج على Habré هنا .

 #include <math.h> #include <stdio.h> #include <time.h> int main(int argc, char **argv) { double count; // k  1+2^30  2^31 for(unsigned long long int i=1073741825 ;i<=2147483648 ;i++) { count=count+1.0/i; } printf("Hn = %.12f ", count); double seconds = clock() / (double) CLOCKS_PER_SEC; printf("  %f  \n", seconds); return 0; } 

عادةً ما تحدد بيئة تطوير متكاملة (ID) عبر الإنترنت وقت تنفيذ البرامج بخمس ثوانٍ ، لذلك يمكن التحقق من هذا البرنامج فقط في بعض بيئة تطوير متكاملة على الإنترنت ، على سبيل المثال ، في onlinegdb.com أو repl.it
بالنسبة إلى k من 1 + 2 ^ 30 إلى 2 ^ 31 ، سيكون وقت التشغيل حوالي 5 ثوانٍ.
بالنسبة إلى k من 1 + 2 ^ 31 إلى 2 ^ 32 ، سيكون وقت التشغيل حوالي 10 ثوانٍ.
بالنسبة إلى k من 1 + 2 ^ 32 إلى 2 ^ 33 ، سيكون وقت التشغيل حوالي 20 ثانية.
بالنسبة إلى k من 1 + 2 ^ 33 إلى 2 ^ 34 ، سيكون وقت التشغيل حوالي 40 ثانية.
بالنسبة إلى k من 1 + 2 ^ 34 إلى 2 ^ 35 ، سيكون وقت التشغيل أكثر من دقيقة واحدة.
...
بالنسبة إلى k من 1 + 2 ^ 45 إلى 2 ^ 46 ، سيكون وقت التشغيل أكثر من 24 ساعة.

افترض أنه بالنسبة لـ k من 1 + 2 ^ 30 إلى 2 ^ 31 ، يكون وقت تنفيذ الخوارزمية هو ~ 2 ثانية.
ثم بالنسبة إلى k = 2 ^ (30 + n) ، فإن وقت تنفيذ الخوارزمية هو 2 ^ n ثانية. (في $$$n \ in \ mathbb {N}$ )
هذه الخوارزمية لديها تعقيد الأسي .

العودة إلى الوحدات.
في حساب التفاضل والتكامل لا يتجزأ ، يتم استخدام الوحدة النمطية في الصيغة

$$

$$\ int \ frac {1} {x} dx = \ int \ frac {dx} {x} = ln \ left | س \ الحق | + C$$

على هابري كان هناك مقال اللوغاريتم الأكثر طبيعية الذي يعتبر هذا التكامل وعلى أساس حسابه لعدد $$$e$ .

وجود الوحدة في الصيغة $$$\ int \ frac {dx} {x} = ln \ left | س \ الحق | + C$ مزيد من الأدلة في "مسار التفاضل والتكامل لا يتجزأ"

إذا ...$$ $ مضمنة $ x <0 $ مضمنة ، ومن خلال التمييز ، من السهل التحقق من ذلك $$$\ left [ln (-x) \ right] '= \ frac {1} {x}$

التطبيق المادي للتكامل $$$\ int \ frac {dx} {x}$

يستخدم هذا التكامل لحساب الفرق المحتمل في لوحات مكثف أسطواني.


"الكهرباء والمغناطيسية":

تم العثور على الفرق المحتمل بين اللوحات من خلال التكامل:

$$

$$\ varphi_ {1} - \ varphi_ {2} = \ int \ limit_ {R_ {1}} ^ {R_ {2}} E (r) dr = \ frac {q} {2 \ pi \ varepsilon_ {0} \ varepsilon l} \ int \ limit_ {R_ {1}} ^ {R_ {2}} \ frac {dr} {r} = \ frac {q} {2 \ pi \ varepsilon_ {0} \ varepsilon l} ln \ frac {R_ {2}} {R_ {1}}$$

( $$$R_ {1}$ و $$$R_ {2}$ - نصف قطر الألواح الداخلية والخارجية).

لا يتم استخدام علامة الوحدة هنا تحت علامة اللوغاريتم الطبيعي $$$ln \ left | \ frac {R_ {2}} {R_ {1}} \ right |$ بسبب $$$R_ {1}$ و $$$R_ {2}$ إيجابية للغاية وهذا الشكل من التسجيل زائدة عن الحاجة.

"وحدات" الرسم

باستخدام الوحدات النمطية ، يمكنك رسم أشكال مختلفة.

إذا كان في برنامج geogebra اكتب الصيغة $$ نحن نحصل عليها



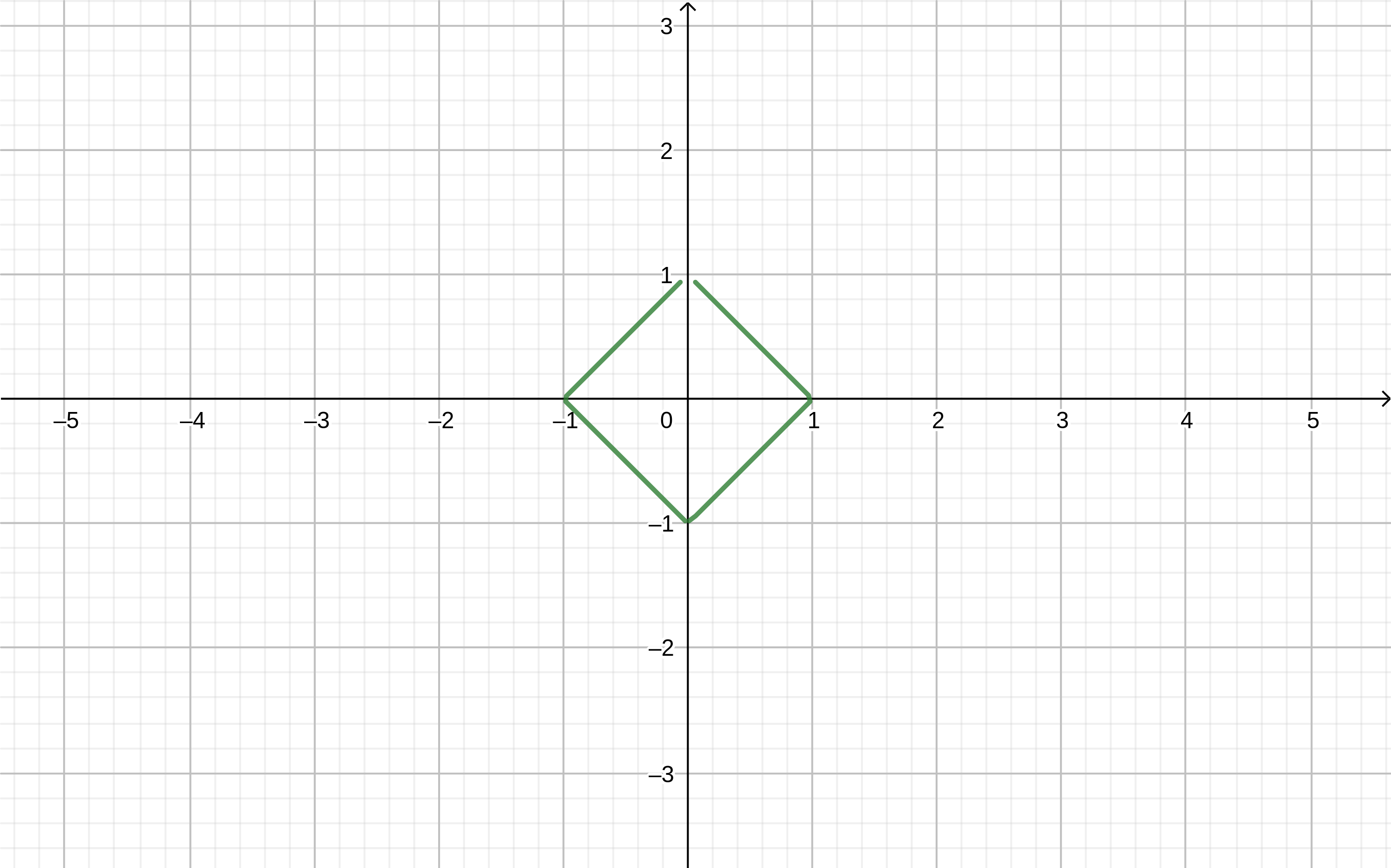
يمكنك رسم أشكال أكثر تعقيدًا. لنرسم ، على سبيل المثال ، "فراشة" في سحابة WolframAlpha

$$

$$\ sum \ frac {\ left | س \ الحق | } {n- \ left | س \ الحق | } + \ frac {\ left | x + n \ right | } {n} + \ frac {\ left | x-n \ right | } {n}$$

قطعة أرض [Sum [abs (x) / (n-abs (x)) + abs (x + n) / (n) + abs (xn) / (n) ، {n ، 1،20}] ، {x ، -60.60}]
في هذا التعبير $$$ن$ يكمن في المدى من $$$1$ قبل $$ . $$$x$ يكمن في المدى من $$ قبل $$ .
رابط إلى الصورة.

الكتب:

"كتاب مهام توجيه الشخصية" M.I. باشماكوف
دورة الفيزياء العامة: في 3 مجلدات T. 2. "الكهرباء والمغناطيسية" I.V. سافيليف