فهم Q- التعلم ، مشكلة "المشي على صخرة"

مرحبا يا هبر! أوجه انتباهكم إلى ترجمة مقالة "فهم Q-Learning ، ومشكلة Cliff Walking" للمخرج Lucas Vazquez .

في آخر مشاركة ، قدمنا ​​مشكلة "المشي على صخرة" واستقرنا على خوارزمية رهيبة لا معنى لها. هذه المرة سوف نكشف أسرار هذا المربع الرمادي ونرى أنه ليس مخيفًا على الإطلاق.

ملخص

لقد توصلنا إلى أنه من خلال تعظيم مقدار المكافآت المستقبلية ، نجد أيضًا أسرع طريق إلى الهدف ، لذا فإن هدفنا الآن هو إيجاد طريقة للقيام بذلك!

مقدمة في Q-Learning

• لنبدأ بإنشاء جدول يقيس مدى أداء إجراء معين في أي ولاية (يمكننا قياسه بقيمة عددية بسيطة ، وبالتالي كلما كانت القيمة أكبر ، كان الإجراء أفضل)
• سيكون لهذا الجدول صف واحد لكل ولاية وعمود واحد لكل إجراء. في عالمنا ، تحتوي الشبكة على 48 ولاية (4 بحلول Y في 12 بواسطة X) ويسمح بـ 4 إجراءات (أعلى ، أسفل ، يسار ، يمين) ، وبالتالي سيكون الجدول 48 × 4.
• تسمى القيم المخزنة في هذا الجدول "قيم Q".
• هذه هي تقديرات مقدار المكافآت المستقبلية. بمعنى آخر ، يقدرون مقدار المكافآت الإضافية التي يمكن أن نحصل عليها قبل نهاية اللعبة ، وأن نكون في الحالة "S" ويقومون بإجراء "أ".
• نقوم بتهيئة الجدول بقيم عشوائية (أو بعض الثابت ، على سبيل المثال ، كل الأصفار).

يحتوي "Q-table" الأمثل على قيم تتيح لنا اتخاذ أفضل الإجراءات في كل ولاية ، مما يتيح لنا أفضل طريقة للفوز في النهاية. تم حل المشكلة ، هتافات ، روبوت اللوردات :).

قيم Q من الدول الخمس الأولى.

كيو التعلم

• كيو التعلم هو خوارزمية "يتعلم" هذه القيم.
• في كل خطوة نحصل على مزيد من المعلومات حول العالم.
• يتم استخدام هذه المعلومات لتحديث القيم في الجدول.

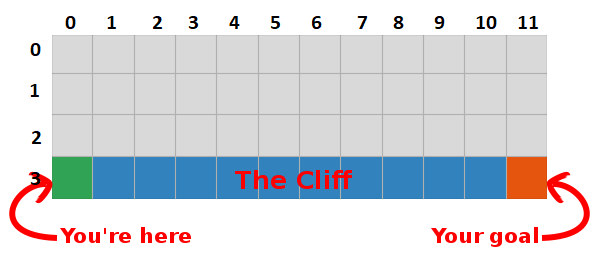
على سبيل المثال ، افترض أننا على بعد خطوة واحدة من الهدف (المربع [2 ، 11]) ، وإذا قررنا النزول ، فسنحصل على مكافأة 0 بدلاً من -1.
يمكننا استخدام هذه المعلومات لتحديث قيمة زوج إجراء الحالة في جدولنا ، وفي المرة التالية التي سنقوم بزيارتها ، سنعرف بالفعل أن الانتقال لأسفل يمنحنا مكافأة قدرها 0.

الآن يمكننا نشر هذه المعلومات إلى أبعد من ذلك! بما أننا نعرف الآن الطريق إلى الهدف من المربع [2 ، 11] ، فإن أي إجراء يؤدي بنا إلى المربع [2 ، 11] سيكون جيدًا أيضًا ، وبالتالي نقوم بتحديث قيمة Q للمربع ، والتي تقودنا إلى [2 ، 11] لتكون أقرب إلى 0.

وهذا ، سيداتي وسادتي ، هو جوهر تعلم Q!

يرجى ملاحظة أنه في كل مرة نصل فيها إلى الهدف ، نقوم بزيادة "خريطتنا" الخاصة بكيفية تحقيق الهدف بمربع واحد ، لذلك بعد عدد كاف من التكرارات ، سيكون لدينا خريطة كاملة توضح لنا كيفية الوصول إلى الهدف من كل ولاية.

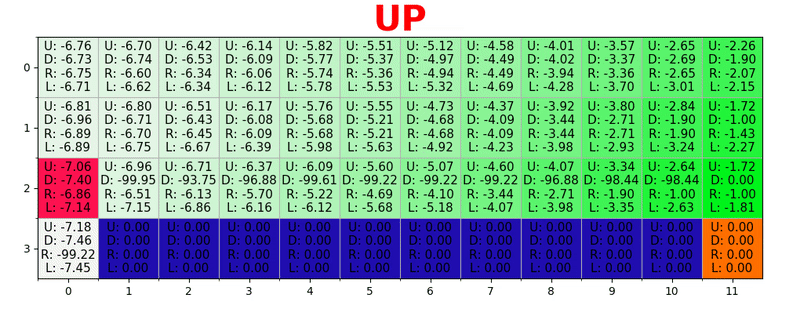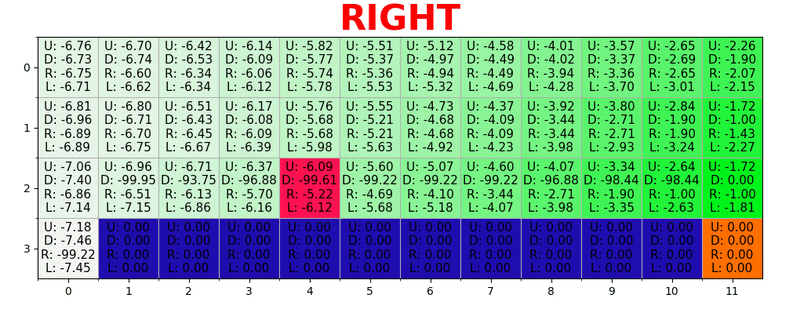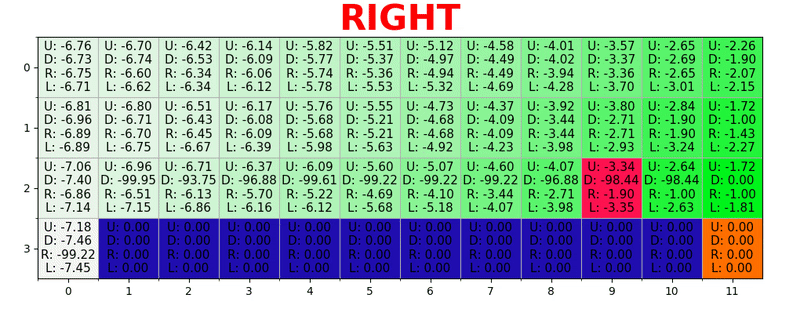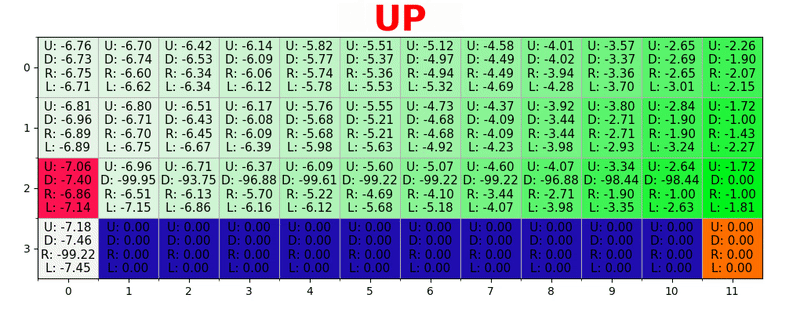يتم إنشاء مسار من خلال اتخاذ أفضل الإجراءات في كل ولاية. يمثل المفتاح الأخضر معنى إجراء أفضل ، وتمثل المفاتيح الأكثر تشبعًا قيمة أعلى. يمثل النص قيمة لكل إجراء (للأعلى والأسفل واليمين واليسار).

معادلة بيلمان

قبل أن نتحدث عن الكود ، دعونا نتحدث عن الرياضيات: المفهوم الأساسي لتعلم Q ، معادلة Bellman.

• أولاً دعنا ننسى في هذه المعادلة
• تنص المعادلة على أن قيمة Q لزوج عمل معين يجب أن تكون المكافأة المستلمة عند الانتقال إلى حالة جديدة (عن طريق تنفيذ هذا الإجراء) ، وتضاف إلى قيمة أفضل إجراء في الحالة التالية.

بمعنى آخر ، ننشر معلومات حول قيم الإجراءات خطوة واحدة في كل مرة!

ولكن يمكننا أن نقرر أن تلقي مكافأة الآن هو أكثر قيمة من تلقي مكافأة في المستقبل ، وبالتالي لدينا γ ، رقم من 0 إلى 1 (عادة من 0.9 إلى 0.99) مضروب في مكافأة في المستقبل ، خصم المكافآت المستقبلية.

لذلك ، بالنظر إلى γ = 0.9 وتطبيق ذلك على بعض حالات عالمنا (الشبكة) ، لدينا:

يمكننا مقارنة هذه القيم مع ما ورد أعلاه في GIF ونرى أنها هي نفسها.

تطبيق

الآن بعد أن أصبح لدينا فهم بديهي لكيفية عمل Q-Learning ، يمكننا أن نبدأ في التفكير في تنفيذ كل هذا ، وسوف نستخدم كود Q-Learning الكاذب من كتاب Sutton كدليل.

الرمز الزائف من كتاب ساتون.

الرمز:

# Initialize Q arbitrarily, in this case a table full of zeros q_values = np.zeros((num_states, num_actions)) # Iterate over 500 episodes for _ in range(500): state = env.reset() done = False # While episode is not over while not done: # Choose action action = egreedy_policy(q_values, state, epsilon=0.1) # Do the action next_state, reward, done = env.step(action) # Update q_values td_target = reward + gamma * np.max(q_values[next_state]) td_error = td_target - q_values[state][action] q_values[state][action] += learning_rate * td_error # Update state state = next_state 

• أولاً ، نقول: "بالنسبة لجميع الولايات والإجراءات ، نقوم بتهيئة Q (s ، a) بشكل تعسفي" ، وهذا يعني أنه يمكننا إنشاء جدول قيم Q لدينا بأي قيم نحبها ، ويمكن أن تكون عشوائية ، ويمكنها أن يكون أي نوع من دائم لا يهم. نرى أنه في السطر 2 نقوم بإنشاء جدول مليء بالأصفار.

نقول أيضًا: "قيمة Q للحالات النهائية هي صفر" ، لا يمكننا اتخاذ أي إجراء في الولايات النهائية ، وبالتالي فإننا نعتبر أن قيمة جميع الإجراءات في هذه الحالة هي صفر.

• في كل حلقة ، يتعين علينا "تهيئة S" ، إنها مجرد وسيلة خيالية لقول "إعادة تشغيل اللعبة" ، وفي حالتنا ، يعني وضع اللاعب في وضع البداية ؛ في عالمنا هناك طريقة تفعل ذلك بالضبط ، ونحن نسميها على السطر 6.
• لكل خطوة زمنية (في كل مرة نحتاج إلى العمل) ، يجب علينا اختيار الإجراء الذي تم الحصول عليه من Q.

تذكر ، "هل نتخذ الإجراءات الأكثر قيمة في كل حالة؟

عندما نفعل ذلك ، نستخدم قيم Q الخاصة بنا لإنشاء السياسة ؛ في هذه الحالة ، ستكون سياسة جشعة ، لأننا نتخذ دائمًا إجراءات ، في رأينا ، هي الأفضل في كل ولاية ، لذلك يقال إننا نتصرف بجشع.

الزباله

ولكن هناك مشكلة في هذا النهج: تخيل أننا في متاهة لها جائزتان ، إحداهما +1 ، والآخر + 100 (وفي كل مرة نجد واحدة منها ، تنتهي اللعبة). نظرًا لأننا نتخذ دائمًا إجراءات نعتبرها الأفضل ، فسوف نلتزم بالجائزة الأولى التي تم العثور عليها ، ونعود إليها دائمًا ، لذلك ، إذا عرفنا جائزة +1 ، فسوف نفتقد جائزة +100 الكبرى.

الحل

نحن بحاجة إلى التأكد من أننا درسنا عالمنا بما فيه الكفاية (هذه مهمة صعبة بشكل مثير للدهشة). هذا هو المكان الذي يأتي فيه اللعب. ε في الخوارزمية الجشعة تعني أنه يجب علينا أن نتصرف بشغف ، ولكن للقيام بأعمال عشوائية كنسبة مئوية من ε بمرور الوقت ، لذلك مع عدد لا حصر له من المحاولات ، يجب علينا فحص جميع الولايات.

يتم اختيار الإجراء وفقًا لهذه الإستراتيجية في السطر 12 ، مع epsilon = 0.1 ، مما يعني أننا نجري بحثًا حول العالم 10٪ من الوقت. تنفيذ السياسة كما يلي:

 def egreedy_policy(q_values, state, epsilon=0.1): # Get a random number from a uniform distribution between 0 and 1, # if the number is lower than epsilon choose a random action if np.random.random() < epsilon: return np.random.choice(4) # Else choose the action with the highest value else: return np.argmax(q_values[state]) 

في السطر 14 في القائمة الأولى ، نسمي طريقة الخطوة لأداء الإجراء ، ويعيدنا العالم إلى الحالة التالية ، والمكافأة والمعلومات حول نهاية اللعبة.

العودة إلى الرياضيات:

لدينا معادلة طويلة ، دعونا نفكر في ذلك:

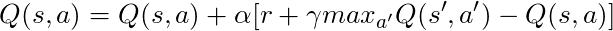
إذا أخذنا α = 1:

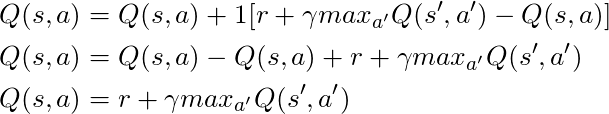
الذي يطابق معادلة بيلمان بالضبط ، والتي رأيناها قبل بضع فقرات! لذلك نحن نعلم بالفعل أن هذا هو الخط المسؤول عن نشر المعلومات حول قيم الدولة.

ولكن عادةً ما تكون α (المعروفة غالبًا باسم سرعة التعلم) أقل من 1 ، فإن هدفها الرئيسي هو تجنب التغييرات الكبيرة في تحديث واحد ، لذا بدلاً من الانتقال إلى الهدف ، فإننا نقترب منه ببطء. في منهجنا الجدولي ، لا يسبب الإعداد α = 1 أي مشاكل ، ولكن عند العمل مع الشبكات العصبية (المزيد حول هذا الموضوع في المقالات التالية) ، يمكن لكل شيء بسهولة الخروج عن السيطرة.

بالنظر إلى الكود ، نرى أنه في السطر 16 في القائمة الأولى التي حددناها td_target ، هذه هي القيمة التي يجب أن نقترب منها ، ولكن بدلاً من الانتقال مباشرة إلى هذه القيمة في السطر 17 ، نحسب td_error ، وسنستخدم هذه القيمة مع السرعة تعلم التحرك ببطء نحو الهدف.

تذكر أن هذه المعادلة هي كيان Q- التعلم.

الآن نحن بحاجة فقط إلى تحديث حالتنا ، وكل شيء جاهز ، هذا هو السطر 20. نكرر هذه العملية حتى نصل إلى نهاية الحلقة ، أو نموت في الصخور أو نصل إلى الهدف.

الخاتمة

الآن نحن نفهم بشكل حدسي ونعرف كيفية تشفير Q-Learning (على الأقل إصدار جدولي) ، تأكد من التحقق من جميع التعليمات البرمجية المستخدمة لهذا المنشور ، المتاحة على جيثب .

تصور اختبار عملية التعلم:

يرجى ملاحظة أن جميع الإجراءات تبدأ بقيمة تتجاوز قيمتها النهائية ، وهذه خدعة لتحفيز استكشاف العالم.