لقد ناقشنا بالفعل محرك فهرسة PostgreSQL وواجهة طرق الوصول ، وكذلك مؤشر التجزئة ، أحد طرق الوصول. سننظر الآن في B-tree ، وهو المؤشر الأكثر استخدامًا والأكثر استخدامًا على نطاق واسع. هذه المقالة كبيرة ، لذا كن صبورًا.

بتري

هيكل

نوع فهرس B-tree ، الذي يتم تنفيذه كطريقة وصول "btree" ، مناسب للبيانات التي يمكن فرزها. بمعنى آخر ، يجب تحديد عوامل التشغيل "أكبر" و "أكبر أو متساوية" و "أقل" و "أقل أو متساوية" و "متساوية" لنوع البيانات. لاحظ أنه في بعض الأحيان يمكن فرز البيانات نفسها بشكل مختلف ، مما يعيدنا إلى مفهوم عائلة المشغل.

كما هو الحال دائمًا ، يتم تجميع صفوف فهرس الشجرة B في الصفحات. في صفحات الأوراق ، تحتوي هذه الصفوف على بيانات يتم فهرستها (مفاتيح) وإشارات إلى صفوف الجدول (TID). في الصفحات الداخلية ، يشير كل صف إلى صفحة فرعية من الفهرس ويحتوي على الحد الأدنى للقيمة في هذه الصفحة.

تحتوي الأشجار B على بعض السمات المهمة:

• B الأشجار متوازنة ، أي ، يتم فصل كل صفحة ورقة من الجذر عن طريق نفس العدد من الصفحات الداخلية. لذلك ، ابحث عن أي قيمة تأخذ نفس الوقت.
  
• B- الأشجار متعددة الفروع ، أي أن كل صفحة (عادة 8 كيلو بايت) يحتوي على الكثير من (مئات) TIDs. ونتيجة لذلك ، فإن عمق الأشجار B صغير جدًا ، حيث يصل في الواقع إلى 5 إلى 5 الجداول الكبيرة جدًا.
  
• يتم فرز البيانات الموجودة في الفهرس بترتيب غير متزايد (بين الصفحات وداخل كل صفحة) ، ويتم توصيل الصفحات ذات المستوى الواحد ببعضها البعض من خلال قائمة ثنائية الاتجاه. لذلك ، يمكننا الحصول على مجموعة من البيانات المطلوبة فقط عن طريق قائمة المشي واحد أو الاتجاه الآخر دون العودة إلى الجذر في كل مرة.
  

يوجد أدناه مثال مبسط للفهرس في حقل واحد مع مفاتيح عدد صحيح.



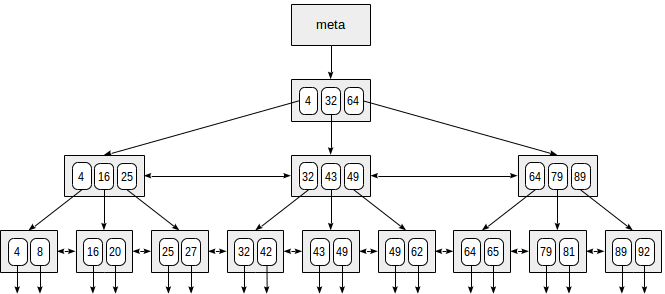
الصفحة الأولى من الفهرس عبارة عن ملف تعريف يشير إلى جذر الفهرس. توجد العقد الداخلية أسفل الجذر ، وتكون صفحات الأوراق في الصف السفلي. تمثل الأسهم لأسفل مراجع من العقد الورقية إلى صفوف الجدول (TIDs).

البحث عن طريق المساواة

دعنا نفكر في البحث عن قيمة في شجرة بحالة " indexed-field = expression ". قل ، نحن مهتمون بمفتاح 49.



يبدأ البحث بالعقدة الجذرية ، ونحتاج إلى تحديد أي من العقد الفرعية التي ستنزل. لكوننا على دراية بالمفاتيح الموجودة في عقدة الجذر (4 ، 32 ، 64) ، فإننا بالتالي نتعرف على نطاقات القيمة في العقد الفرعية. منذ 32 ≤ 49 <64 ، نحتاج إلى النزول إلى العقدة الفرعية الثانية. بعد ذلك ، يتم تكرار نفس العملية بشكل متكرر حتى نصل إلى عقدة ورقة يمكن من خلالها الحصول على معرّفات الكود.

في الواقع ، هناك عدد من التفاصيل تعقد هذه العملية التي تبدو بسيطة. على سبيل المثال ، يمكن أن يحتوي الفهرس على مفاتيح غير فريدة ويمكن أن يكون هناك الكثير من القيم المتساوية بحيث لا تناسب صفحة واحدة. بالعودة إلى مثالنا ، يبدو أنه يجب علينا النزول من العقدة الداخلية على الإشارة إلى قيمة 49. ولكن ، كما هو واضح من الشكل ، بهذه الطريقة سنقوم بتخطي أحد مفاتيح "49" في صفحة الورقة السابقة . لذلك ، بمجرد أن نجد مفتاحًا مساويًا تمامًا في صفحة داخلية ، يتعين علينا أن ننزلق موضعًا واحدًا يسارًا ثم نلقي نظرة على صفوف فهرس المستوى الأساسي من اليسار إلى اليمين بحثًا عن المفتاح المطلوب.

(هناك تعقيد آخر وهو أنه أثناء البحث ، يمكن لعمليات أخرى تغيير البيانات: يمكن إعادة إنشاء الشجرة ، ويمكن تقسيم الصفحات إلى قسمين ، إلخ. تم تصميم جميع الخوارزميات بحيث لا تتداخل هذه العمليات مع بعضها البعض ولا تتسبب في أقفال إضافية كلما كان ذلك ممكنًا ، لكننا سنتجنب التوسع في هذا.)

البحث عن طريق عدم المساواة

عند البحث بالشرط " تعبير الحقل المفهرس " (أو " تعبير الحقل المفهرس ") ، نجد أولاً قيمة (إن وجدت) في الفهرس بواسطة شرط المساواة " مفهرسة حقل = تعبير " ثم نتجول خلال صفحات ورقة في الاتجاه المناسب حتى النهاية.

يوضح الشكل هذه العملية لـ n ≤ 35:



يتم دعم المشغلين "الأكبر" و "الأقل" بطريقة مماثلة ، باستثناء أنه يجب إسقاط القيمة الموجودة في البداية.

البحث عن طريق النطاق

عند البحث عن طريق النطاق " expression1 ≤ indexed-field ≤ expression2 " ، نجد قيمة حسب الحالة " indexed-field = expression1 " ، ثم نستمر في السير خلال صفحات الورقة أثناء استيفاء الشرط " indexed-field ≤ expression2 " ؛ أو بالعكس: ابدأ بالتعبير الثاني وامش في اتجاه معاكس حتى نصل إلى التعبير الأول.

يوضح الشكل هذه العملية للحالة 23 ≤ n ≤ 64:

مثال

لنلقِ نظرة على مثال عن شكل خطط الاستعلام. كالعادة ، نستخدم قاعدة البيانات التجريبية ، وهذه المرة سننظر في جدول الطائرات. يحتوي على أقل من تسعة صفوف ، وسيختار المخطط عدم استخدام الفهرس لأن الجدول بأكمله يناسب صفحة واحدة. لكن هذا الجدول مثير للاهتمام بالنسبة لنا لغرض توضيحي.

demo=# select * from aircrafts; 

  aircraft_code | model | range ---------------+---------------------+------- 773 | Boeing 777-300 | 11100 763 | Boeing 767-300 | 7900 SU9 | Sukhoi SuperJet-100 | 3000 320 | Airbus A320-200 | 5700 321 | Airbus A321-200 | 5600 319 | Airbus A319-100 | 6700 733 | Boeing 737-300 | 4200 CN1 | Cessna 208 Caravan | 1200 CR2 | Bombardier CRJ-200 | 2700 (9 rows) 

 demo=# create index on aircrafts(range); demo=# set enable_seqscan = off; 

(أو بشكل صريح ، "إنشاء فهرس على الطائرات باستخدام btree (النطاق)" ، ولكنه عبارة عن شجرة B تم إنشاؤها افتراضيًا.)

البحث عن طريق المساواة:

 demo=# explain(costs off) select * from aircrafts where range = 3000; 

  QUERY PLAN --------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: (range = 3000) (2 rows) 

البحث عن طريق عدم المساواة:

 demo=# explain(costs off) select * from aircrafts where range < 3000; 

  QUERY PLAN --------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: (range < 3000) (2 rows) 

وحسب النطاق:

 demo=# explain(costs off) select * from aircrafts where range between 3000 and 5000; 

  QUERY PLAN ----------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: ((range >= 3000) AND (range <= 5000)) (2 rows) 

الفرز

لنؤكد مرة أخرى على النقطة التي تشير إلى أنه مع أي نوع من المسح (الفهرسة أو الفهرسة فقط أو الصورة النقطية) ، تقوم طريقة الوصول "btree" بإرجاع البيانات المطلوبة ، والتي يمكننا رؤيتها بوضوح في الأشكال أعلاه.

لذلك ، إذا كان الجدول يحتوي على فهرس في حالة الفرز ، فسوف يأخذ المُحسِّن في الاعتبار كلا الخيارين: مسح فهرس الجدول ، والذي يُرجع بسهولة البيانات المصنفة ، والمسح المتسلسل للجدول مع الفرز التالي للنتيجة.

ترتيب الفرز

عند إنشاء فهرس ، يمكننا تحديد ترتيب الفرز بشكل صريح. على سبيل المثال ، يمكننا إنشاء فهرس من خلال نطاقات الرحلات بهذه الطريقة على وجه الخصوص:

 demo=# create index on aircrafts(range desc); 

في هذه الحالة ، ستظهر القيم الأكبر في الشجرة على اليسار ، بينما تظهر القيم الأصغر على اليمين. لماذا يمكن أن يكون ذلك ضروريًا إذا تمكنا من متابعة القيم المفهرسة في أي من الاتجاهين؟

والغرض من فهارس متعددة الأعمدة. لنقم بإنشاء عرض لإظهار طرازات الطائرات ذات التقسيم التقليدي إلى حرفة قصيرة ومتوسطة وطويلة المدى:

 demo=# create view aircrafts_v as select model, case when range < 4000 then 1 when range < 10000 then 2 else 3 end as class from aircrafts; demo=# select * from aircrafts_v; 

  model | class ---------------------+------- Boeing 777-300 | 3 Boeing 767-300 | 2 Sukhoi SuperJet-100 | 1 Airbus A320-200 | 2 Airbus A321-200 | 2 Airbus A319-100 | 2 Boeing 737-300 | 2 Cessna 208 Caravan | 1 Bombardier CRJ-200 | 1 (9 rows) 

ولنقم بإنشاء فهرس (باستخدام التعبير):

 demo=# create index on aircrafts( (case when range < 4000 then 1 when range < 10000 then 2 else 3 end), model); 

الآن يمكننا استخدام هذا الفهرس للحصول على بيانات مرتبة حسب كلا العمودين بالترتيب التصاعدي:

 demo=# select class, model from aircrafts_v order by class, model; 

  class | model -------+--------------------- 1 | Bombardier CRJ-200 1 | Cessna 208 Caravan 1 | Sukhoi SuperJet-100 2 | Airbus A319-100 2 | Airbus A320-200 2 | Airbus A321-200 2 | Boeing 737-300 2 | Boeing 767-300 3 | Boeing 777-300 (9 rows) 

 demo=# explain(costs off) select class, model from aircrafts_v order by class, model; 

  QUERY PLAN -------------------------------------------------------- Index Scan using aircrafts_case_model_idx on aircrafts (1 row) 

وبالمثل ، يمكننا تنفيذ الاستعلام لفرز البيانات بترتيب تنازلي:

 demo=# select class, model from aircrafts_v order by class desc, model desc; 

  class | model -------+--------------------- 3 | Boeing 777-300 2 | Boeing 767-300 2 | Boeing 737-300 2 | Airbus A321-200 2 | Airbus A320-200 2 | Airbus A319-100 1 | Sukhoi SuperJet-100 1 | Cessna 208 Caravan 1 | Bombardier CRJ-200 (9 rows) 

 demo=# explain(costs off) select class, model from aircrafts_v order by class desc, model desc; 

  QUERY PLAN ----------------------------------------------------------------- Index Scan BACKWARD using aircrafts_case_model_idx on aircrafts (1 row) 

ومع ذلك ، لا يمكننا استخدام هذا الفهرس للحصول على بيانات مرتبة حسب عمود واحد بترتيب تنازلي وحسب العمود الآخر بترتيب تصاعدي. سيتطلب ذلك الفرز بشكل منفصل:

 demo=# explain(costs off) select class, model from aircrafts_v order by class ASC, model DESC; 

  QUERY PLAN ------------------------------------------------- Sort Sort Key: (CASE ... END), aircrafts.model DESC -> Seq Scan on aircrafts (3 rows) 

(لاحظ أنه ، كملاذ أخير ، اختار المخطط المسح المتسلسل بغض النظر عن إعداد "enable_seqscan = off" الذي تم إجراؤه مسبقًا. وهذا لأن هذا الإعداد لا يمنع في الواقع مسح الجدول ، ولكنه يحدد فقط التكلفة الفلكية - يرجى النظر في الخطة باستخدام "التكاليف على".)

لجعل هذا الاستعلام يستخدم الفهرس ، يجب أن يتم بناء الأخير مع اتجاه الفرز المطلوب:

 demo=# create index aircrafts_case_asc_model_desc_idx on aircrafts( (case when range < 4000 then 1 when range < 10000 then 2 else 3 end) ASC, model DESC); demo=# explain(costs off) select class, model from aircrafts_v order by class ASC, model DESC; 

  QUERY PLAN ----------------------------------------------------------------- Index Scan using aircrafts_case_asc_model_desc_idx on aircrafts (1 row) 

ترتيب الأعمدة

هناك مشكلة أخرى تنشأ عند استخدام فهارس متعددة الأعمدة وهي ترتيب إدراج أعمدة في فهرس. بالنسبة إلى B-tree ، هذا الترتيب ذو أهمية كبيرة: سيتم فرز البيانات داخل الصفحات حسب الحقل الأول ، ثم حسب الحقل الثاني ، وهكذا.

يمكننا تمثيل الفهرس الذي قمنا ببنائه على فترات ونماذج المدى بطريقة رمزية على النحو التالي:



في الواقع فإن مثل هذا الفهرس الصغير سوف يناسب صفحة جذر واحدة بالتأكيد. في الشكل ، يتم توزيعه عمدا بين عدة صفحات من أجل الوضوح.

يتضح من هذا المخطط أن البحث حسب المسميات مثل "class = 3" (ابحث فقط حسب الحقل الأول) أو "class = 3 and model = 'Boeing 777-300'" (البحث عن طريق كلا الحقلين) سيعمل بكفاءة.

ومع ذلك ، سيكون البحث حسب المعيار "model = 'Boeing 777-300'" أقل فعالية: بدءًا من الجذر ، لا يمكننا تحديد أي عقدة تابعة تنزل ، وبالتالي ، سيتعين علينا النزول إليها جميعًا. هذا لا يعني أنه لا يمكن استخدام فهرس مثل هذا - حيث أن كفاءته في مشكلة. على سبيل المثال ، إذا كان لدينا ثلاث فئات من الطائرات والعديد من الطرز في كل فئة ، فسنضطر إلى البحث في حوالي ثلث الفهرس ، وقد يكون هذا أكثر فعالية من الفحص الكامل للطاولة ... أو لا.

ومع ذلك ، إذا أنشأنا فهرسًا مثل هذا:

 demo=# create index on aircrafts( model, (case when range < 4000 then 1 when range < 10000 then 2 else 3 end)); 

سيتغير ترتيب الحقول:



باستخدام هذا الفهرس ، ستعمل عملية البحث حسب المسند "model = 'Boeing 777-300'" بكفاءة ، ولكن البحث حسب المسند "class = 3" لن يعمل.

لاغية

فهرسة أسلوب الوصول "Btree" وتدعم البحث حسب الشروط IS NULL و IS NOT NULL.

لنأخذ في الاعتبار جدول الرحلات ، حيث تحدث القيم الخالية:

 demo=# create index on flights(actual_arrival); demo=# explain(costs off) select * from flights where actual_arrival is null; 

  QUERY PLAN ------------------------------------------------------- Bitmap Heap Scan on flights Recheck Cond: (actual_arrival IS NULL) -> Bitmap Index Scan on flights_actual_arrival_idx Index Cond: (actual_arrival IS NULL) (4 rows) 

توجد NULLs على واحد أو الطرف الآخر من العقد الورقية اعتمادًا على كيفية إنشاء الفهرس (NULLS FIRST أو NULLS LAST). هذا مهم إذا كان الاستعلام يتضمن الفرز: يمكن استخدام الفهرس إذا كان أمر SELECT يحدد نفس ترتيب NULLs في جملة ORDER BY كترتيب محدد للفهرس المدمج (NULLS FIRST أو NULLS LAST).

في المثال التالي ، هذه الأوامر هي نفسها ، وبالتالي ، يمكننا استخدام الفهرس:

 demo=# explain(costs off) select * from flights order by actual_arrival NULLS LAST; 

  QUERY PLAN -------------------------------------------------------- Index Scan using flights_actual_arrival_idx on flights (1 row) 

وهنا تختلف هذه الطلبات ، ويختار المُحسِّن المسح المتسلسل مع الفرز التالي:

 demo=# explain(costs off) select * from flights order by actual_arrival NULLS FIRST; 

  QUERY PLAN ---------------------------------------- Sort Sort Key: actual_arrival NULLS FIRST -> Seq Scan on flights (3 rows) 

لاستخدام الفهرس ، يجب أن يتم إنشاؤه باستخدام NULLs الموجودة في البداية:

 demo=# create index flights_nulls_first_idx on flights(actual_arrival NULLS FIRST); demo=# explain(costs off) select * from flights order by actual_arrival NULLS FIRST; 

  QUERY PLAN ----------------------------------------------------- Index Scan using flights_nulls_first_idx on flights (1 row) 

من المؤكد أن مشكلات مثل هذه ناجمة عن عدم وجود خانات خالية ، أي نتيجة المقارنة لـ NULL وأي قيمة أخرى غير محددة:

 demo=# \pset null NULL demo=# select null < 42; 

  ?column? ---------- NULL (1 row) 

هذا يتعارض مع مفهوم B- شجرة ولا تنسجم مع النمط العام. ومع ذلك ، تلعب القيم الخالية دورًا مهمًا في قواعد البيانات التي يتعين علينا دائمًا تقديم استثناءات لها.

نظرًا لأنه يمكن فهرسة NULLs ، فمن الممكن استخدام فهرس حتى دون أي شروط مفروضة على الجدول (نظرًا لأن الفهرس يحتوي على معلومات حول كافة صفوف الجدول بالتأكيد). قد يكون هذا منطقيًا إذا تطلب الاستعلام ترتيب البيانات ويضمن الفهرس الترتيب المطلوب. في هذه الحالة ، يمكن للمخطط اختيار الوصول إلى الفهرس للحفظ في عملية فرز منفصلة.

خصائص

دعونا نلقي نظرة على خصائص طريقة الوصول "btree" ( تم تقديم الاستعلامات بالفعل ).

  amname | name | pg_indexam_has_property --------+---------------+------------------------- btree | can_order | t btree | can_unique | t btree | can_multi_col | t btree | can_exclude | t 

كما رأينا ، يمكن لـ B-tree طلب البيانات ودعم التفرد - وهذه هي طريقة الوصول الوحيدة لتزويدنا بخصائص مثل هذه. فهارس متعددة الأعمدة مسموح بها أيضًا ، لكن طرق الوصول الأخرى (وإن لم تكن كلها) قد تدعم أيضًا هذه الفهارس. سنناقش دعم تقييد EXCLUDE في المرة القادمة ، وليس بدون سبب.

  name | pg_index_has_property ---------------+----------------------- clusterable | t index_scan | t bitmap_scan | t backward_scan | t 

تدعم طريقة الوصول "Btree" كلا التقنيتين للحصول على القيم: مسح الفهرس ، وكذلك المسح النقطي. وكما نرى ، يمكن لطريقة الوصول السير عبر الشجرة "للأمام" و "للخلف".

  name | pg_index_column_has_property --------------------+------------------------------ asc | t desc | f nulls_first | f nulls_last | t orderable | t distance_orderable | f returnable | t search_array | t search_nulls | t 

تشرح الخصائص الأربعة الأولى لهذه الطبقة كيف يتم ترتيب قيم عمود معين بالضبط. في هذا المثال ، يتم فرز القيم بترتيب تصاعدي ("asc") ويتم توفير NULLs أخيرًا ("nulls_last"). ولكن كما رأينا بالفعل ، هناك مجموعات أخرى ممكنة.

تشير خاصية "Search_array" إلى دعم التعبيرات مثل هذا بواسطة الفهرس:

 demo=# explain(costs off) select * from aircrafts where aircraft_code in ('733','763','773'); 

  QUERY PLAN ----------------------------------------------------------------- Index Scan using aircrafts_pkey on aircrafts Index Cond: (aircraft_code = ANY ('{733,763,773}'::bpchar[])) (2 rows) 

تشير خاصية "المرتجعة" إلى دعم الفحص الفهرس فقط ، وهو أمر معقول نظرًا لأن الصفوف الخاصة بفهرسة مخزن الفهرسة هي القيم نفسها (على عكس مؤشر التجزئة ، على سبيل المثال). من المنطقي هنا قول بضع كلمات حول تغطية الفهارس القائمة على شجرة B.

فهارس فريدة مع صفوف إضافية

كما ناقشنا سابقًا ، فإن فهرس التغطية هو الذي يخزن كل القيم المطلوبة للاستعلام ، والوصول إلى الجدول نفسه غير مطلوب (تقريبًا). يمكن أن يكون الفهرس فريد يغطي على وجه التحديد.

ولكن لنفترض أننا نريد إضافة أعمدة إضافية مطلوبة للاستعلام إلى الفهرس الفريد. ومع ذلك ، لا يضمن تفرد مثل هذه القيم المركبة تفرد المفتاح ، وستكون هناك حاجة إلى فهارسين على نفس الأعمدة: واحد فريد لدعم قيود السلامة والآخر لاستخدامه كغطاء. هذا غير فعال بالتأكيد.

في شركتنا Anastasiya Lubennikova lubennikovaav ، تم تحسين طريقة "btree" بحيث يمكن إدراج أعمدة إضافية غير فريدة في فهرس فريد. نأمل أن يتم تبني هذا التصحيح من قبل المجتمع ليصبح جزءًا من PostgreSQL ، لكن هذا لن يحدث في وقت مبكر من الإصدار 10. في هذه المرحلة ، يتوفر التصحيح في Pro Standard 9.5+ ، وهذا ما يبدو عليه مثل

في الواقع كان هذا التصحيح ملتزمًا بـ PostgreSQL 11.

لننظر في جدول الحجوزات:

 demo=# \d bookings 

  Table "bookings.bookings" Column | Type | Modifiers --------------+--------------------------+----------- book_ref | character(6) | not null book_date | timestamp with time zone | not null total_amount | numeric(10,2) | not null Indexes: "bookings_pkey" PRIMARY KEY, btree (book_ref) Referenced by: TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) REFERENCES bookings(book_ref) 

في هذا الجدول ، يتم توفير المفتاح الأساسي (book_ref ، رمز الحجز) من خلال فهرس "btree" عادي. لنقم بإنشاء فهرس فريد جديد مع عمود إضافي:

 demo=# create unique index bookings_pkey2 on bookings(book_ref) INCLUDE (book_date); 

الآن نستبدل المؤشر الحالي بمؤشر جديد (في المعاملة ، لتطبيق جميع التغييرات في وقت واحد):

 demo=# begin; demo=# alter table bookings drop constraint bookings_pkey cascade; demo=# alter table bookings add primary key using index bookings_pkey2; demo=# alter table tickets add foreign key (book_ref) references bookings (book_ref); demo=# commit; 

هذا هو ما حصلنا عليه:

 demo=# \d bookings 

  Table "bookings.bookings" Column | Type | Modifiers --------------+--------------------------+----------- book_ref | character(6) | not null book_date | timestamp with time zone | not null total_amount | numeric(10,2) | not null Indexes: "bookings_pkey2" PRIMARY KEY, btree (book_ref) INCLUDE (book_date) Referenced by: TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) REFERENCES bookings(book_ref) 

الآن يعمل الفهرس نفسه على أنه فريد ويعمل بمثابة فهرس تغطية لهذا الاستعلام ، على سبيل المثال:

 demo=# explain(costs off) select book_ref, book_date from bookings where book_ref = '059FC4'; 

  QUERY PLAN -------------------------------------------------- Index Only Scan using bookings_pkey2 on bookings Index Cond: (book_ref = '059FC4'::bpchar) (2 rows) 

إنشاء الفهرس

من المعروف ، ولكن ليس أقل أهمية ، أنه بالنسبة لجدول كبير الحجم ، من الأفضل تحميل البيانات هناك بدون فهارس وإنشاء فهارس مطلوبة لاحقًا. هذا ليس أسرع فقط ، ولكن على الأرجح سيكون حجم الفهرس أصغر.

الشيء هو أن إنشاء فهرس "btree" يستخدم عملية أكثر فاعلية من الإدراج القيم للصف في الشجرة. تقريبًا ، يتم فرز جميع البيانات المتوفرة في الجدول ، ويتم إنشاء صفحات ورقة من هذه البيانات. ثم يتم بناء الصفحات الداخلية على هذه القاعدة حتى يتحول الهرم بأكمله إلى الجذر.

تعتمد سرعة هذه العملية على حجم ذاكرة الوصول العشوائي المتاحة ، والتي تقتصر على المعلمة "maintenance_work_mem". لذلك ، زيادة قيمة المعلمة يمكن تسريع العملية. بالنسبة إلى الفهارس الفريدة ، يتم تخصيص ذاكرة الحجم "work_mem" بالإضافة إلى "maintenance_work_mem".

دلالات المقارنة

لقد ذكرنا في المرة الأخيرة أن PostgreSQL بحاجة إلى معرفة وظائف التجزئة التي يجب الاتصال بها للحصول على قيم من أنواع مختلفة وأن هذا الارتباط يتم تخزينه في طريقة وصول "التجزئة". وبالمثل ، يجب على النظام معرفة كيفية ترتيب القيم. هذا ضروري للفرز ، والتجمعات (في بعض الأحيان) ، وصناديق الدمج ، وهلم جرا. لا يرتبط PostgreSQL بأسماء عوامل التشغيل (مثل> ، <، =) نظرًا لأن المستخدمين يمكنهم تحديد نوع البيانات الخاص بهم وإعطاء المشغلين المقابلين أسماء مختلفة. عائلة المشغل التي تستخدمها طريقة الوصول "btree" تحدد أسماء المشغلين بدلاً من ذلك.

على سبيل المثال ، يتم استخدام عوامل المقارنة هذه في عائلة مشغل "bool_ops":

 postgres=# select amop.amopopr::regoperator as opfamily_operator, amop.amopstrategy from pg_am am, pg_opfamily opf, pg_amop amop where opf.opfmethod = am.oid and amop.amopfamily = opf.oid and am.amname = 'btree' and opf.opfname = 'bool_ops' order by amopstrategy; 

  opfamily_operator | amopstrategy ---------------------+-------------- <(boolean,boolean) | 1 <=(boolean,boolean) | 2 =(boolean,boolean) | 3 >=(boolean,boolean) | 4 >(boolean,boolean) | 5 (5 rows) 

هنا يمكننا أن نرى خمسة عوامل مقارنة ، ولكن كما ذكرنا سابقًا ، يجب ألا نعتمد على أسمائهم. لمعرفة المقارنة بين كل مشغل ، يتم تقديم مفهوم الاستراتيجية. يتم تحديد خمس استراتيجيات لوصف دلالات المشغل:

• 1 - أقل
• 2 - أقل أو متساو
• 3 - متساو
• 4 - أكبر أو مساوي
• 5 - أكبر

يمكن أن تحتوي بعض عائلات المشغلين على عدة مشغلين يقومون بتنفيذ استراتيجية واحدة. على سبيل المثال ، تحتوي عائلة مشغل "integer_ops" على العوامل التالية للاستراتيجية 1:

 postgres=# select amop.amopopr::regoperator as opfamily_operator from pg_am am, pg_opfamily opf, pg_amop amop where opf.opfmethod = am.oid and amop.amopfamily = opf.oid and am.amname = 'btree' and opf.opfname = 'integer_ops' and amop.amopstrategy = 1 order by opfamily_operator; 

  opfamily_operator ---------------------- <(integer,bigint) <(smallint,smallint) <(integer,integer) <(bigint,bigint) <(bigint,integer) <(smallint,integer) <(integer,smallint) <(smallint,bigint) <(bigint,smallint) (9 rows) 

بفضل هذا ، يمكن للمحسن تجنب أنواع الكتابة عند مقارنة قيم الأنواع المختلفة الموجودة في عائلة مشغل واحد.

دعم الفهرس لنوع بيانات جديد

توفر الوثائق مثالًا على إنشاء نوع بيانات جديد للأرقام المعقدة وفئة عامل لفرز القيم من هذا النوع. يستخدم هذا المثال لغة C ، وهو أمر معقول تمامًا عندما تكون السرعة حرجة. ولكن لا يوجد شيء يمنعنا من استخدام SQL خالص لنفس التجربة من أجل محاولة فهم دلالات المقارنة وفهمها بشكل أفضل.

لنقم بإنشاء نوع مركب جديد مع حقلين: الأجزاء الحقيقية والخيالية.

 postgres=# create type complex as (re float, im float); 

يمكننا إنشاء جدول بحقل من النوع الجديد وإضافة بعض القيم إلى الجدول:

 postgres=# create table numbers(x complex); postgres=# insert into numbers values ((0.0, 10.0)), ((1.0, 3.0)), ((1.0, 1.0)); 

الآن يطرح سؤال: كيف تطلب أرقامًا معقدة إذا لم يتم تحديد علاقة ترتيب لها بالمعنى الرياضي؟

كما اتضح ، يتم تحديد عوامل المقارنة بالفعل بالنسبة لنا:

 postgres=# select * from numbers order by x; 

  x -------- (0,10) (1,1) (1,3) (3 rows) 

بشكل افتراضي ، يكون الفرز مكونًا لنوع مركب: تتم مقارنة الحقول الأولى ، ثم الحقول الثانية ، وهكذا ، تقريبًا بنفس الطريقة التي تتم بها مقارنة سلاسل النص بحرف. ولكن يمكننا تحديد ترتيب مختلف. على سبيل المثال ، يمكن التعامل مع الأعداد المركبة كنواقل وترتيبها بواسطة المعامل (الطول) ، والذي يتم حسابه على أنه الجذر التربيعي لمجموع مربعات الإحداثيات (نظرية فيثاغورس). لتعريف مثل هذا الطلب ، دعنا ننشئ وظيفة مساعدة تحسب المعامل:

 postgres=# create function modulus(a complex) returns float as $$ select sqrt(a.re*a.re + a.im*a.im); $$ immutable language sql; 

الآن سوف نحدد بشكل منهجي الوظائف لجميع مشغلي المقارنة الخمسة باستخدام هذه الوظيفة الإضافية:

 postgres=# create function complex_lt(a complex, b complex) returns boolean as $$ select modulus(a) < modulus(b); $$ immutable language sql; postgres=# create function complex_le(a complex, b complex) returns boolean as $$ select modulus(a) <= modulus(b); $$ immutable language sql; postgres=# create function complex_eq(a complex, b complex) returns boolean as $$ select modulus(a) = modulus(b); $$ immutable language sql; postgres=# create function complex_ge(a complex, b complex) returns boolean as $$ select modulus(a) >= modulus(b); $$ immutable language sql; postgres=# create function complex_gt(a complex, b complex) returns boolean as $$ select modulus(a) > modulus(b); $$ immutable language sql; 

وسنقوم بإنشاء مشغلي المقابلة. لتوضيح أنهم لا يحتاجون إلى أن يطلق عليهم ">" ، "<" ، وهكذا ، فلنمنحهم أسماء "غريبة".

 postgres=# create operator #<#(leftarg=complex, rightarg=complex, procedure=complex_lt); postgres=# create operator #<=#(leftarg=complex, rightarg=complex, procedure=complex_le); postgres=# create operator #=#(leftarg=complex, rightarg=complex, procedure=complex_eq); postgres=# create operator #>=#(leftarg=complex, rightarg=complex, procedure=complex_ge); postgres=# create operator #>#(leftarg=complex, rightarg=complex, procedure=complex_gt); 

في هذه المرحلة ، يمكننا مقارنة الأرقام:

 postgres=# select (1.0,1.0)::complex #<# (1.0,3.0)::complex; 

  ?column? ---------- t (1 row) 

بالإضافة إلى خمسة عوامل تشغيل ، تتطلب طريقة الوصول "btree" تحديد وظيفة أخرى (مفرطة ولكنها ملائمة): يجب أن تُرجع -1 أو 0 أو 1 إذا كانت القيمة الأولى أقل من أو تساوي أو تزيد عن الثانية واحد وتسمى هذه الوظيفة الإضافية الدعم. قد تتطلب طرق الوصول الأخرى تحديد وظائف الدعم الأخرى.

 postgres=# create function complex_cmp(a complex, b complex) returns integer as $$ select case when modulus(a) < modulus(b) then -1 when modulus(a) > modulus(b) then 1 else 0 end; $$ language sql; 

نحن الآن على استعداد لإنشاء فئة عامل تشغيل (وسيتم إنشاء عائلة عامل التشغيل بنفس الاسم تلقائيًا):

 postgres=# create operator class complex_ops default for type complex using btree as operator 1 #<#, operator 2 #<=#, operator 3 #=#, operator 4 #>=#, operator 5 #>#, function 1 complex_cmp(complex,complex); 

فرز الآن يعمل كما هو مطلوب:

 postgres=# select * from numbers order by x; 

  x -------- (1,1) (1,3) (0,10) (3 rows) 

وبالتأكيد سيتم دعمها بواسطة مؤشر "btree".

لإكمال الصورة ، يمكنك الحصول على وظائف الدعم باستخدام هذا الاستعلام:

 postgres=# select amp.amprocnum, amp.amproc, amp.amproclefttype::regtype, amp.amprocrighttype::regtype from pg_opfamily opf, pg_am am, pg_amproc amp where opf.opfname = 'complex_ops' and opf.opfmethod = am.oid and am.amname = 'btree' and amp.amprocfamily = opf.oid; 

  amprocnum | amproc | amproclefttype | amprocrighttype -----------+-------------+----------------+----------------- 1 | complex_cmp | complex | complex (1 row) 

الداخلية

يمكننا استكشاف البنية الداخلية لشجرة B باستخدام ملحق "pageinspect".

 demo=# create extension pageinspect; 

ملف تعريف الفهرس:

 demo=# select * from bt_metap('ticket_flights_pkey'); 

  magic | version | root | level | fastroot | fastlevel --------+---------+------+-------+----------+----------- 340322 | 2 | 164 | 2 | 164 | 2 (1 row) 

الأكثر إثارة للاهتمام هنا هو مستوى الفهرس: الفهرس الموجود في عمودين لجدول به مليون صف مطلوبة بأقل من مستويين (لا يشمل الجذر).

معلومات إحصائية عن المجموعة 164 (الجذر):

 demo=# select type, live_items, dead_items, avg_item_size, page_size, free_size from bt_page_stats('ticket_flights_pkey',164); 

  type | live_items | dead_items | avg_item_size | page_size | free_size ------+------------+------------+---------------+-----------+----------- r | 33 | 0 | 31 | 8192 | 6984 (1 row) 

والبيانات الموجودة في المربع (حقل "البيانات" ، الذي يتم التضحية به هنا لعرض الشاشة ، تحتوي على قيمة مفتاح الفهرسة في التمثيل الثنائي):

 demo=# select itemoffset, ctid, itemlen, left(data,56) as data from bt_page_items('ticket_flights_pkey',164) limit 5; 

  itemoffset | ctid | itemlen | data ------------+---------+---------+---------------------------------------------------------- 1 | (3,1) | 8 | 2 | (163,1) | 32 | 1d 30 30 30 35 34 33 32 33 30 35 37 37 31 00 00 ff 5f 00 3 | (323,1) | 32 | 1d 30 30 30 35 34 33 32 34 32 33 36 36 32 00 00 4f 78 00 4 | (482,1) | 32 | 1d 30 30 30 35 34 33 32 35 33 30 38 39 33 00 00 4d 1e 00 5 | (641,1) | 32 | 1d 30 30 30 35 34 33 32 36 35 35 37 38 35 00 00 2b 09 00 (5 rows) 

يتعلق العنصر الأول بالتقنيات ويحدد الحد الأعلى لجميع العناصر في الكتلة (تفاصيل التنفيذ التي لم نناقشها) ، بينما تبدأ البيانات نفسها بالعنصر الثاني. من الواضح أن العقدة الفرعية الموجودة في أقصى اليسار هي الكتلة 163 ، تليها الكتلة 323 ، وهكذا. هم ، بدوره ، يمكن استكشافها باستخدام نفس الوظائف.

الآن ، وفقًا لتقليد جيد ، من المنطقي قراءة الوثائق و README وشفرة المصدر.

ومع ذلك ، هناك ملحق آخر يحتمل أن يكون مفيدًا هو " amcheck " ، والذي سيتم دمجه في PostgreSQL 10 ، وبالنسبة للإصدارات الأقل ، يمكنك الحصول عليه من github . يتحقق هذا الامتداد من الاتساق المنطقي للبيانات الموجودة في الأشجار B ويمكننا من اكتشاف الأخطاء مسبقًا.

هذا صحيح ، "amcheck" جزء من PostgreSQL يبدأ من الإصدار 10.

اقرأ على .