أخيرًا ، ظهر دليل باللغة الروسية للغة جوليا . إنه يوفر مقدمة كاملة للغة لأولئك الذين لديهم خبرة قليلة في البرمجة (سيكون الباقي مفيدًا للتطوير العام) ، وهناك أيضًا مقدمة للتعلم الآلي ومجموعة من المهام لتوحيد المواد.
خلال البحث ، صادفت دورة برمجة للاقتصاديين (بالإضافة إلى جوليا ، هناك أيضًا بيثون). يمكن للخبرة الذهاب لدورة تدريبية سريعة أو قراءة كتاب " كيف تفكر كأنك عالم كمبيوتر"
فيما يلي ترجمة لمواد من مدونة Christopher Rackauckas 7 Julia Gotchas وكيفية التعامل معها
اسمحوا لي أن أبدأ بالقول إن جوليا هي لغة رائعة. أنا أحبها ، وهذا ما أعتبره أقوى لغة وبديهية استخدمتها على الإطلاق. هذه بلا شك لغتي المفضلة. ومع ذلك ، هناك بعض "المزالق" ، أشياء صغيرة صعبة تحتاج إلى معرفته. كل لغة بها ، وأحد الأشياء الأولى التي يجب عليك القيام بها لإتقان اللغة هي معرفة ما هي وكيفية تجنبها. الهدف من هذا المنشور هو مساعدتك في تسريع هذه العملية من خلال الكشف عن بعض
جوليا هي لغة جيدة لفهم ما يحدث ، لأنه لا يوجد سحر فيها. أراد مطورو جوليا أن يكون لديهم قواعد سلوك محددة بوضوح. هذا يعني أنه يمكن شرح كل السلوك. ومع ذلك ، قد يعني هذا أنه عليك الضغط على رأسك لفهم سبب حدوث ذلك وليس الآخر. هذا هو السبب في أنني لن أعرض فقط بعض المشكلات الشائعة ، لكني سأشرح أيضًا سبب ظهورها. سترى أن هناك بعض الأنماط المتشابهة للغاية ، وبمجرد أن تصبح على دراية بها ، فلن تتمكن من الخروج عن أي منها. لهذا السبب ، لدى جوليا منحنى تعليمي أكثر حدة بعض الشيء مقارنة باللغات الأكثر بساطة مثل MATLAB / R / Python . ومع ذلك ، بمجرد أن تتقن هذا ، ستتمكن من الاستفادة الكاملة من ثغرات جوليا في الحصول على أداء C / Fortran . الآن حفر أعمق.
بشكل غير متوقع: لدى REPL (محطة) نطاق عالمي
هذه هي إلى حد بعيد المشكلة الأكثر شيوعًا التي أبلغ عنها مستخدمو جوليا الجدد. سيقول أحدهم: "سمعت ، جوليا سريعة!" ، افتح REPL ، أكتب بسرعة بعض الخوارزمية المعروفة وقم بتنفيذ هذا البرنامج النصي. بعد تنفيذها ، ينظرون إلى الوقت ويقولون: "انتظر ثانية ، لماذا يكون بطيئًا ، كما هو الحال في بيثون؟" نظرًا لأن هذه مشكلة مهمة وشائعة ، فلنقضي بعض الوقت في استكشاف أسباب حدوث ذلك لمعرفة كيفية تجنب ذلك.
استطراد صغير: لماذا جوليا سريعة
يجب أن تفهم أن جوليا ليست مجرد تجميع للشفرة ، بل هي أيضًا تخصص للأنواع (أي ، تجميع للشفرات الخاصة بهذه الأنواع). اسمحوا لي أن أكرر: جوليا ليست سريعة ، لأن الشفرة يتم تجميعها باستخدام برنامج التحويل البرمجي JIT ، ولكن سر السرعة هو أن الشفرة الخاصة بالنوع يتم تجميعها.
إذا كنت بحاجة إلى قصة كاملة ، تحقق من بعض الملاحظات التي كتبتها في الندوة القادمة . يتم تحديد خصوصية النوع حسب المبدأ الأساسي لتصميم جوليا: الإرسال المتعدد . عند كتابة الرمز:
function f(a,b) return 2a+b end
يبدو أن هذه f(2.0,3.0) ، f(2.0,3.0) جوليا الكود المترجم الذي يأخذ رقمين 2a + b ويعيد 2a + b . إذا اتصلت بـ f(2,3) ، فسوف تقوم جوليا بتشغيل شفرة مترجمة أخرى تأخذ عددين صحيحين وتُرجع 2a + b . الدالة f عبارة عن تجريد أو اختصار للعديد من الطرق المختلفة التي لها نفس الشكل ، ويطلق على مخطط استخدام الرمز f لاستدعاء كل هذه الطرق المختلفة إرسال متعدد. وهذا ينطبق في كل مكان: عامل التشغيل + هو في الواقع وظيفة تستدعي الأساليب اعتمادًا على الأنواع التي يراها. تحصل جوليا في الواقع على سرعتها لأن الشفرة المترجمة بها تعرف أنواعها ، وبالتالي فإن الشفرة المترجمة التي تستدعي f (2.0،3.0) هي بالضبط الكود المترجم الذي تحصل عليه بتحديد الوظيفة نفسها في C / Fortran . يمكنك التحقق من ذلك باستخدام الماكرو code_native لمشاهدة التجميع code_native :
@code_native f(2.0,3.0)
pushq %rbp movq %rsp, %rbp Source line: 2 vaddsd %xmm0, %xmm0, %xmm0 vaddsd %xmm1, %xmm0, %xmm0 popq %rbp retq nop
هذا هو نفس التجميع المترجم الذي تتوقعه من دالة في C / Fortran ، وهو يختلف عن رمز التجميع للأعداد الصحيحة:
@code_native f(2,3) pushq %rbp movq %rsp, %rbp Source line: 2 leaq (%rdx,%rcx,2), %rax popq %rbp retq nopw (%rax,%rax)
الجوهر: REPL / Global Scope لا يسمح بخصوصية النوع
هذا يقودنا إلى النقطة الرئيسية: REPL / Global Scope بطيئة لأنه لا يسمح بمواصفات الكتابة. بادئ ذي بدء ، لاحظ أن REPL نطاق عالمي لأن جوليا تتيح نطاقًا متداخلًا للوظائف. على سبيل المثال ، إذا حددنا
function outer() a = 5 function inner() return 2a end b = inner() return 3a+b end
سوف نرى أن هذا الرمز يعمل. وذلك لأن جوليا تتيح لك التقاط
a=2.0; b=3.0 function linearcombo() return 2a+b end ans = linearcombo()
و
a = 2; b = 3 ans2= linearcombo()
السؤال: ما هي الأنواع التي يجب أن يقبلها المحول البرمجي لـ a و b ؟ لاحظ أنه في هذا المثال ، قمنا بتغيير الأنواع ولا نزال نطلق على نفس الوظيفة. يمكنه التعامل مع أي أنواع نضيفها إليها: عائم ، أعداد صحيحة ، صفائف ، أنواع مستخدمين غريبة ، إلخ. في جوليا ، هذا يعني أن المتغيرات يجب محاصرتها ، ويتم فحص الأنواع في كل مرة يتم استخدامها. ما رأيك في التعليمات البرمجية المترجمة تبدو؟
ضخم pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $96, %rsp movl $2147565792, %edi # imm = 0x800140E0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, %rsi leaq -72(%rbp), %r14 movq $0, -88(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -72(%rbp) movq $0, -56(%rbp) movq $10, -104(%rbp) movq (%rsi), %rax movq %rax, -96(%rbp) leaq -104(%rbp), %rax movq %rax, (%rsi) Source line: 3 movq pcre2_default_compile_context_8(%rdi), %rax movq %rax, -56(%rbp) movl $2154391480, %eax # imm = 0x806967B8 vmovq %rax, %xmm0 vpslldq $8, %xmm0, %xmm0 # xmm0 = zero,zero,zero,zero,zero,zero,zero,zero,xmm0[0,1,2,3,4,5,6,7] vmovdqu %xmm0, -80(%rbp) movq %rdi, -64(%rbp) movabsq $jl_apply_generic, %r15 movl $3, %edx movq %r14, %rcx callq *%r15 movq %rax, %rbx movq %rbx, -88(%rbp) movabsq $586874896, %r12 # imm = 0x22FB0010 movq (%r12), %rax testq %rax, %rax jne L198 leaq 98096(%rdi), %rcx movabsq $jl_get_binding_or_error, %rax movl $122868360, %edx # imm = 0x752D288 callq *%rax movq %rax, (%r12) L198: movq 8(%rax), %rax testq %rax, %rax je L263 movq %rax, -80(%rbp) addq $5498232, %rdi # imm = 0x53E578 movq %rdi, -72(%rbp) movq %rbx, -64(%rbp) movq %rax, -56(%rbp) movl $3, %edx movq %r14, %rcx callq *%r15 movq -96(%rbp), %rcx movq %rcx, (%rsi) addq $96, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r14 popq %r15 popq %rbp retq L263: movabsq $jl_undefined_var_error, %rax movl $122868360, %ecx # imm = 0x752D288 callq *%rax ud2 nopw (%rax,%rax)
بالنسبة إلى اللغات الديناميكية بدون تخصص الكتابة ، تكون هذه الشفرة المتضخمة مع جميع التعليمات الإضافية جيدة قدر الإمكان ، لذلك فإن جوليا تبطئ من سرعتها. لفهم سبب أهمية ذلك ، لاحظ أن كل جزء من التعليمات البرمجية التي تكتبها في مجموعات جوليا. دعنا نقول أنك تكتب حلقة في البرنامج النصي الخاص بك:
a = 1 for i = 1:100 a += a + f(a) end
سيتعين على المحول البرمجي ترجمة هذه الحلقة ، ولكن نظرًا لأنه لا يمكن أن يضمن عدم تغيير الأنواع ، فإنه يلتف بشكل متحفظ بقاعدة قدم على جميع الأنواع ، مما يؤدي إلى إبطاء التنفيذ.
كيفية تجنب مشكلة
هناك عدة طرق لتجنب هذه المشكلة. أسهل طريقة هي دائمًا التفاف البرامج النصية في الوظائف. على سبيل المثال ، سوف يأخذ الرمز السابق النموذج:
function geta(a) # can also just define a=1 here for i = 1:100 a += a + f(a) end return a end a = geta(1)
سوف يمنحك هذا النتيجة نفسها ، لكن بما أن المترجم يمكنه التخصص في النوع a ، فسوف يوفر لك الشفرة المترجمة التي تريدها. شيء آخر يمكنك القيام به هو تحديد المتغيرات الخاصة بك كما الثوابت.
const b = 5
من خلال القيام بذلك ، تخبر المترجم أن المتغير لن يتغير ، وبالتالي سيكون بإمكانه تخصيص كل الكود الذي يستخدمه على النوع الموجود حاليًا. هناك غرابة طفيفة تسمح لك جوليا بالفعل بتغيير قيمة الثابت ، ولكن ليس من النوع. وبالتالي ، يمكنك استخدام const لإعلام المترجم أنك لن تقوم بتغيير النوع. ومع ذلك ، لاحظ أن هناك بعض المراوغات الصغيرة:
const a = 5 f() = a println(f()) # Prints 5 a = 6 println(f()) # Prints 5 # WARNING: redefining constant a
هذا لا يعمل كما هو متوقع ، لأن المترجم ، يدرك أنه يعرف الإجابة على f () = a (بما أن الثابت) ، ببساطة استبدل استدعاء الوظيفة بالإجابة ، مما أعطى سلوكًا مختلفًا عن إذا a يكن ثابتًا.
الأخلاقية: لا تكتب البرامج النصية مباشرة في REPL ، فقم دائمًا بلفها في إحدى الوظائف.
Nezhdanchik اثنين: اكتب عدم الاستقرار
لذلك ، لقد أعربت للتو عن رأي بشأن مدى أهمية التخصص في الشفرة لأنواع البيانات. اسمحوا لي أن أطرح عليك سؤالاً ، ماذا يحدث عندما يمكن أن تتغير أنواعك؟ إذا خمنت: "حسنًا ، في هذه الحالة ، لا يمكنك تخصيص الشفرة المترجمة" ، فأنت على حق. تعرف هذه المشكلة بعدم استقرار النوع. قد تظهر بشكل مختلف ، ولكن أحد الأمثلة الشائعة هو أنك تقوم بتهيئة القيمة بالقيمة البسيطة ، ولكن ليس بالضرورة بالنوع الذي ينبغي أن تكون عليه. على سبيل المثال ، دعنا ننظر إلى:
function g() x=1 for i = 1:10 x = x/2 end return x end
لاحظ أن 1/2 هو رقم النقطة العائمة في جوليا. لذلك ، إذا بدأنا بـ x = 1 ، فإن الرقم الصحيح سيتغير إلى رقم الفاصلة العائمة ، وبالتالي ، يجب أن تقوم الدالة بترجمة الحلقة الداخلية ، كما لو كانت من أي نوع. إذا بدلاً من ذلك كان لدينا:
function h() x=1.0 for i = 1:10 x = x/2 end return x end
عندئذٍ ، ستكون الوظيفة بأكملها قادرة على التحويل البرمجي على النحو الأمثل ، مع العلم أن x ستبقى رقم الفاصلة العائمة (هذه القدرة للمترجم على تحديد الأنواع تسمى type inference). يمكننا التحقق من الشفرة المترجمة لمعرفة الفرق:
موطئ قدم أصلي pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r13 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $136, %rsp movl $2147565728, %ebx # imm = 0x800140A0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, -152(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -80(%rbp) movq $0, -64(%rbp) vxorps %ymm0, %ymm0, %ymm0 vmovups %ymm0, -128(%rbp) movq $0, -96(%rbp) movq $18, -144(%rbp) movq (%rax), %rcx movq %rcx, -136(%rbp) leaq -144(%rbp), %rcx movq %rcx, (%rax) movq $0, -88(%rbp) Source line: 4 movq %rbx, -104(%rbp) movl $10, %edi leaq 477872(%rbx), %r13 leaq 10039728(%rbx), %r15 leaq 8958904(%rbx), %r14 leaq 64(%rbx), %r12 leaq 10126032(%rbx), %rax movq %rax, -160(%rbp) nopw (%rax,%rax) L176: movq %rbx, -128(%rbp) movq -8(%rbx), %rax andq $-16, %rax movq %r15, %rcx cmpq %r13, %rax je L272 movq %rbx, -96(%rbp) movq -160(%rbp), %rcx cmpq $2147419568, %rax # imm = 0x7FFF05B0 je L272 movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %edx leaq -80(%rbp), %rcx movabsq $jl_apply_generic, %rax vzeroupper callq *%rax movq %rax, -88(%rbp) jmp L317 nopw %cs:(%rax,%rax) L272: movq %rcx, -120(%rbp) movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %r8d leaq -80(%rbp), %rdx movabsq $jl_invoke, %rax vzeroupper callq *%rax movq %rax, -112(%rbp) L317: movq (%rax), %rsi movl $1488, %edx # imm = 0x5D0 movl $16, %r8d movq -152(%rbp), %rcx movabsq $jl_gc_pool_alloc, %rax callq *%rax movq %rax, %rbx movq %r13, -8(%rbx) movq %rsi, (%rbx) movq %rbx, -104(%rbp) Source line: 3 addq $-1, %rdi jne L176 Source line: 6 movq -136(%rbp), %rax movq -152(%rbp), %rcx movq %rax, (%rcx) movq %rbx, %rax addq $136, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r13 popq %r14 popq %r15 popq %rbp retq nop
ضد
أنيق التجميع الإملائي pushq %rbp movq %rsp, %rbp movabsq $567811336, %rax # imm = 0x21D81D08 Source line: 6 vmovsd (%rax), %xmm0 # xmm0 = mem[0],zero popq %rbp retq nopw %cs:(%rax,%rax)
هذا الفارق في عدد العمليات الحسابية للحصول على نفس القيمة!
كيفية البحث عن نوع عدم الاستقرار والتعامل معه

في هذه المرحلة ، قد تسأل: "حسنًا ، لماذا لا تستخدم C فقط حتى لا تضطر إلى البحث عن أوجه عدم الاستقرار هذه؟" الجواب هو:
- من السهل العثور عليها
- قد تكون مفيدة.
يمكنك التعامل مع عدم الاستقرار مع الحواجز الوظيفية
يمنحك Julia الماكرو code_warntype لإظهار مكان عدم استقرار النوع. على سبيل المثال ، إذا استخدمنا هذا في دالة g التي أنشأناها:
@code_warntype g()
الحصول على التحليل Variables: #self#::#g x::ANY #temp#@_3::Int64 i::Int64 #temp#@_5::Core.MethodInstance #temp#@_6::Float64 Body: begin x::ANY = 1 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#@_3::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#@_3::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 30 SSAValue(3) = #temp#@_3::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#@_3::Int64,1)) i::Int64 = SSAValue(3) #temp#@_3::Int64 = SSAValue(4) # line 4: unless (Core.isa)(x::UNION{FLOAT64,INT64},Float64)::ANY goto 15 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Float64, ::Int64) goto 24 15: unless (Core.isa)(x::UNION{FLOAT64,INT64},Int64)::ANY goto 19 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Int64, ::Int64) goto 24 19: goto 21 21: #temp#@_6::Float64 = (x::UNION{FLOAT64,INT64} / 2)::Float64 goto 26 24: #temp#@_6::Float64 = $(Expr(:invoke, :(#temp#@_5), :(Main./), :(x::Union{Float64,Int64}), 2)) 26: x::ANY = #temp#@_6::Float64 28: goto 5 30: # line 6: return x::UNION{FLOAT64,INT64} end::UNION{FLOAT64,INT64}
لاحظ أنه في البداية نقول أن النوع x هو Any . ستستخدم أي نوع لم يتم تحديده كنوع strict type ، أي أنه نوع تجريدي يحتاج إلى محاصر / محدد في كل خطوة. نرى أنه في النهاية نرجع x كـ UNION {FLOAT64, INT64} ، وهو نوع آخر غير صارم. هذا يخبرنا أن النوع code_warntype لـ h ، code_warntype على جميع الأنواع الصارمة:
@code_warntype h() Variables: #self#::#h x::Float64 #temp#::Int64 i::Int64 Body: begin x::Float64 = 1.0 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 15 SSAValue(3) = #temp#::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#::Int64,1)) i::Int64 = SSAValue(3) #temp#::Int64 = SSAValue(4) # line 4: x::Float64 = (Base.box)(Base.Float64,(Base.div_float)(x::Float64,(Base.box)(Float64,(Base.sitofp)(Float64,2)))) 13: goto 5 15: # line 6: return x::Float64 end::Float64
يشير هذا إلى أن الوظيفة مستقرة ، وسيتم تجميعها بشكل أساسي في رمز C الأمثل. وبالتالي ، ليس من الصعب العثور على عدم الاستقرار. الأمر الأكثر صعوبة هو العثور على التصميم المناسب. لماذا حل عدم الاستقرار نوع؟ هذه مشكلة طويلة الأمد أدت إلى حقيقة أن اللغات المكتوبة ديناميكيًا تهيمن على مجال تشغيل النصوص. والفكرة هي أنه في كثير من الحالات تريد أن تجد حلا وسطا بين الأداء والموثوقية.
على سبيل المثال ، يمكنك قراءة جدول من صفحة ويب يتم فيها خلط الأعداد الصحيحة مع أرقام الفاصلة العائمة. في جوليا ، يمكنك كتابة وظيفتك بحيث إذا كانت جميعها أعدادًا صحيحة ، فسوف يتم تجميعها جيدًا ، وإذا كانت جميعها أرقام نقطية عائمة ، فسيتم أيضًا تجميعها جيدًا. وإذا كانت مختلطة؟ هذا سوف لا يزال يعمل. هذه هي المرونة / الراحة التي نعرفها ونحبها من لغة مثل Python / R. لكن جوليا ستخبرك مباشرةً ( عبر رمز_النمط ) عند التضحية بالأداء.
كيفية التعامل مع عدم الاستقرار نوع
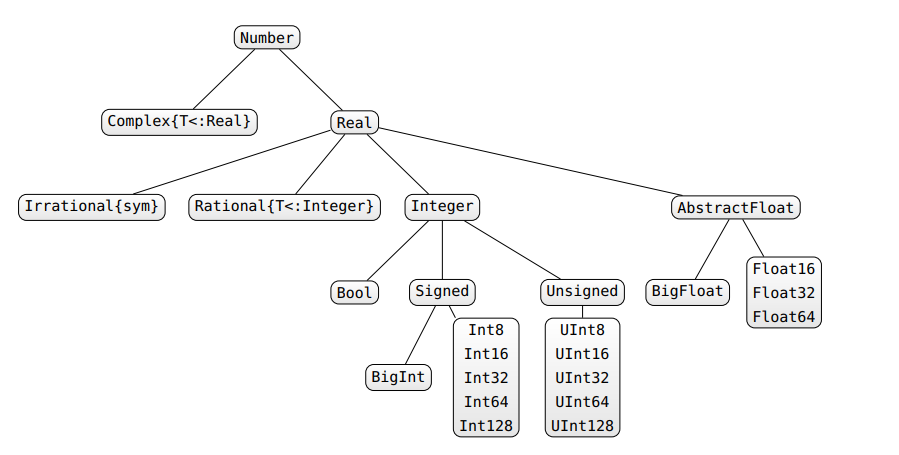
هناك عدة طرق للتعامل مع عدم استقرار النوع. بادئ ذي بدء ، إذا كنت تحب شيئًا مثل C / Fortran حيث يتم الإعلان عن أنواعك ولا يمكن تغييرها (مما يضمن استقرار الكتابة) ، فيمكنك القيام بذلك في جوليا:
local a::Int64 = 5
هذا يجعل عددًا صحيحًا 64 بت ، وإذا حاولت الشفرة المستقبلية تغييره ، سيتم إنشاء رسالة خطأ (أو سيتم إجراء التحويل الصحيح. ولكن نظرًا لأن التحويل لن يتم تقريبه تلقائيًا ، فمن المحتمل أن يتسبب في حدوث أخطاء). يرشهم حول التعليمات البرمجية الخاصة بك وتحصل على استقرار النوع ، علاء ، C / فورتران . هناك طريقة أقل تعقيدًا للتعامل مع هذا باستخدام عبارات الكتابة. هنا يمكنك وضع نفس الصيغة على الجانب الآخر من علامة المساواة. على سبيل المثال:
a = (b/c)::Float64
يبدو أنه يقول: "احسب b / c وتأكد من أن الإخراج هو Float64. إذا لم يكن الأمر كذلك ، فجرّب التحويل التلقائي. إذا تعذر إجراء التحويل بسهولة ، فقم بإخراج خطأ." سيساعدك وضع مثل هذه التصميمات على التأكد من معرفة الأنواع المعنية. ومع ذلك ، في بعض الحالات ، نوع عدم الاستقرار ضروري. على سبيل المثال ، لنفترض أنك تريد الحصول على كود موثوق به ، لكن المستخدم يمنحك شيئًا مجنونًا ، مثل:
arr = Vector{Union{Int64,Float64}}(undef, 4) arr[1]=4 arr[2]=2.0 arr[3]=3.2 arr[4]=1
وهو عبارة عن مجموعة من الأعداد الصحيحة 4 × 1 وأرقام الفاصلة العائمة. نوع العنصر الفعلي للصفيف هو Union {Int64, Float64} ، والذي ، كما رأينا سابقًا ، لم يكن صارمًا ، مما قد يؤدي إلى حدوث مشكلات. يعرف المترجم فقط أن كل قيمة يمكن أن تكون عددًا صحيحًا أو رقمًا عائمًا ، ولكن ليس أي عنصر من أي نوع. هذا يعني أنه من السذاجة القيام بحساب باستخدام هذه المجموعة ، على سبيل المثال:
function foo{T,N}(array::Array{T,N}) for i in eachindex(array) val = array[i] # do algorithm X on val end end
سيكون بطيئا حيث سيتم محاصر العمليات. ومع ذلك ، يمكننا استخدام الإرسال المتعدد لتشغيل الرموز بطريقة متخصصة. هذا هو المعروف باسم استخدام الحواجز الوظيفية. على سبيل المثال:
function inner_foo{T<:Number}(val::T) # Do algorithm X on val end function foo2{T,N}(array::Array{T,N}) for i in eachindex(array) inner_foo(array[i]) end end
لاحظ أنه بسبب الإرسال المتعدد ، فإن استدعاء inner_foo يستدعي إما طريقة مترجمة خصيصًا inner_foo العائمة أو طريقة مترجمة خصيصًا للأعداد الصحيحة. وبالتالي ، يمكنك وضع عملية حسابية طويلة في inner_foo ولا تزال تجعلها تعمل بشكل جيد ، وليس أقل من الكتابة الصارمة التي يوفرها لك الحاجز الوظيفي.
وبالتالي ، آمل أن ترى أن جوليا تقدم مزيجًا جيدًا من أداء الكتابة القوي وراحة الكتابة الديناميكية. لدى جوليا مبرمج جيد الخياران لزيادة الإنتاجية و / أو الإنتاجية إذا لزم الأمر.
مفاجأة 3: إيفال يعمل عالميا

واحدة من أعظم نقاط القوة لدى جوليا هي قدراتها على البرمجة. يتيح لك ذلك بسهولة كتابة برامج لتوليد الكود ، مما يقلل بشكل فعال من حجم الكود الذي تحتاج إلى كتابته وصيانته. الماكرو هو وظيفة يتم تشغيلها في وقت التحويل البرمجي و (عادة) يبصق التعليمات البرمجية. على سبيل المثال:
macro defa() :(a=5) end
سيحل محل أي مثيل defa مع الكود a = 5 ( :(a = 5) مقتبسة من التعبير . كود جوليا هو تعبيرات ، وبالتالي metaprogramming عبارة عن مجموعة من التعبيرات).
يمكنك استخدام هذا لإنشاء أي برنامج جوليا معقد ترغب فيه ووضعه في وظيفة كنوع من الاختصار الذكي حقًا. ومع ذلك ، في بعض الأحيان قد تحتاج إلى تقييم التعليمات البرمجية المنشأة مباشرة. يمنحك Julia دالة eval أو ماكرو eval للقيام بذلك. بشكل عام ، يجب أن تحاول تجنب eval ، ولكن هناك بعض الرموز حيث يكون ذلك ضروريًا ، على سبيل المثال ، مكتبتي الجديدة لنقل البيانات بين العمليات المختلفة للبرمجة المتوازية . , , :
@eval :(a=5)
(REPL). , / . على سبيل المثال:
function testeval() @eval :(a=5) return 2a+5 end
, a REPL. , , :
function testeval() @eval :(a=5) b = a::Int64 return 2b+5 end
b — , , , , , . eval , , REPL .
4:
Julia , . : , .
, ? , , . على سبيل المثال:
a = 2 + 3 + 4 + 5 + 6 + 7 +8 + 9 + 10+ 11+ 12+ 13 a
, 90, 27. ? a = 2 + 3 + 4 + 5 + 6 + 7 , a = 27 , +8 + 9 + 10+ 11+ 12+ 13 , , , :
a = 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10+ 11+ 12+ 13
90, . , .
. — , . rssdev10
. على سبيل المثال:
x = rand(2,2) a = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) -sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)] b = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) - sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)]
, a b — , ! (2,2) , — (1-) 2. , , :
a = [1 -2] b = [1 - 2]
: 1 -2 . : 1-2 . - . :
a = [1 2 3 -4 2 -3 1 4]
2x4. , . : hcat :
a = hcat(cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi),-sin(2.*x[:,1]).*sin(2.*x[:,2])./(4))
!
№5: ,

(View) — () , ( ), .
, , . , . , .
— "". ""
a = [3;4;5] b = a b[1] = 1
, a — [1; 4; 5] , . . b a . , b = a b a . , , b , , ( b a ). , . , , :
a = rand(2,2) # Makes a random 2x2 matrix b = vec(a) # Makes a view to the 2x2 matrix which is a 1-dimensional array
b , b a , b . , , ( , ). . , . على سبيل المثال:
c = a[1:2,1]
c a ). , , , , . , , :
d = @view a[1:2,1] e = view(a,1:2,1)
d , e — , d e a , , , reshape , .) , . على سبيل المثال:
a[1:2,1] = [1;2]
a , a[1:2,1] view (a, 1:2,1) , , a . -? , :
b = copy(a)
, b a , , b a . a , copy! (B, a) , a a ( , b ). . , Vector {Vector} :
a = [ [1, 2, 3], [4, 5], [6, 7, 8, 9] ]
b = copy(a) b[1][1] = 10 a
3-element Array{Array{Int64,1},1}: [10, 2, 3] [4, 5] [6, 7, 8, 9]
, a[1][1] 10! ? copy a . a , b , b . , deepcopy :
b = deepcopy(a)
, . , , .
№6: , In-Place
MATLAB / Python / R . Julia , , , " ".
function f() x = [1;5;6] for i = 1:10 x = x + inner(x) end return x end function inner(x) return 2x end
, inner , , 2x . , . , - y , :
function f() x = [1;5;6] y = Vector{Int64}(3) for i = 1:10 inner(y,x) for i in 1:3 x[i] = x[i] + y[i] end copy!(y,x) end return x end function inner!(y,x) for i=1:3 y[i] = 2*x[i] end nothing end
. inner!(y, x) , y . y , y , , , inner! (y, x) ! ( ).
, inner!(y, x) . copy!(y, x) — , x y , . , , . : x y . , x + inner(x) , , , 11 . , .
, , , . - ( loop-fusion ). Julia v0.5 . ( ( broadcast ), f.(x) — , f x , , . f x , x = x + f. (x) . :
x .= x .+ f.(x)
.= , , ,
for i = 1:length(x) x[i] = x[i] + f(x[i]) end
, :
function f() x = [1;5;6] for i = 1:10 x .= x .+ inner.(x) end return x end function inner(x) return 2x end
MATLAB / R / Python , , , .
: ,
: , . , . , . , , . , .
- , C / Fortran , . - , , !
: ? , . , , ? [ , Javascript var x = 3 x , x = 3 x . ? , - Javascript!]