مقدمة:يرتبط عدد كبير من المشكلات الأكثر تنوعًا المتعلقة بجميع فروع الفيزياء الرياضية تقريبًا والمصممة للإجابة على الأسئلة الفنية الموضعية بتطبيق وظائف Bessel.
تُستخدم وظائف Bessel على نطاق واسع في حل مشكلات الصوتيات والفيزياء الإشعاعية وهيدروديناميكية المياه ومشاكل الفيزياء الذرية والنووية. تعمل العديد من تطبيقات Bessel على نظرية الموصلية الحرارية ونظرية المرونة (مشاكل في اهتزازات الألواح ، ومشاكل نظرية الصدفة ، ومشاكل تحديد تركيز الإجهاد بالقرب من الشقوق).
يتم تفسير هذه الشعبية لوظائف Bessel من خلال حقيقة أن حل معادلات الفيزياء الرياضية التي تحتوي على عامل Laplace في الإحداثيات الأسطوانية بالطريقة الكلاسيكية لفصل المتغيرات يؤدي إلى معادلة تفاضلية عادية ، والتي تعمل على تحديد هذه الوظائف [1].
تتم تسمية وظائف Bessel على اسم عالم الفلك الألماني Friedrich Bessel ، الذي قام في عام 1824 ، وهو يدرس حركة الكواكب حول الشمس ، باستخلاص علاقات التكرار لوظائف Bessel
Jv(x) تلقى للأعداد الصحيحة
v تمثيل لا يتجزأ من وظيفة
Jv(x) ، ثبت وجود عدد لا يحصى من الأصفار لوظيفة
J0(x) وتجميع الجداول الأولى للوظائف
J1(x) و
J2(x) .
ومع ذلك ، لأول مرة واحدة من وظائف بسل
J0(x) اعتبره دانييل برنولي في عام 1732 في عمل مخصص لتذبذب السلاسل الثقيلة. وجد د. برنولي تعبيرًا عن الوظيفة
J0(x) في شكل سلسلة السلطة ولاحظت (بدون دليل) أن المعادلة
J0(x)=0 لديه عدد لا يحصى من جذور صالحة.
العمل التالي ، الذي واجهت فيه وظائف بسل ، كان عمل ليوناردو يولر في عام 1738 ، المكرس لدراسة اهتزازات الغشاء الدائري. في هذا العمل ، وجد L. Euler للأعداد الصحيحة
v وظيفة بسل التعبير
Jv(x) في شكل سلسلة في القوى
x وفي الأوراق اللاحقة مددت هذا التعبير إلى حالة قيم الفهرس التعسفي
v . بالإضافة إلى ذلك ، أثبت L. Euler ذلك من أجل
v يساوي عدد صحيح ونصف ، وظائف
Jv(x) أعرب من خلال وظائف الابتدائية.
ولاحظ (بدون دليل) أنه صحيح
v وظائف
Jv(x) لدينا عدد لا يحصى من الأصفار الحقيقية وقدم تمثيلًا لا يتجزأ من أجل
Jv(x) . يعتقد بعض الباحثين أن النتائج الرئيسية المتعلقة بوظائف Bessel وتطبيقاتها في الفيزياء الرياضية ترتبط باسم L. Euler.
لدراسة خاصية وظائف Bessel وفي الوقت نفسه لإتقان طرق حل المعادلات التي تم اختزالها إلى وظائف Bessel ، يسمح البرنامج الموزع بحرية للرياضيات الرمزية SymPy - مكتبة Python.
في برنامج SymPy للرياضيات الرمزية ، يمكن إنشاء رسوم بيانية لوظائف Bessel من النوع الأول من أوامر الأعداد الصحيحة باستخدام العلاقة لمجموع سلسلة:
Jp(x)= sum inftym=0 fracx2m+p(−1)m22m+pm! غاما(ع+م+1)
وظائف بسل من النوع الأولfrom sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{p}(x)" p1=plot(besselj(0,x),(x,-20,20),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(1,x),(x,-20,20),line_color='g',show=False) p3=plot(besselj(2,x),(x,-20,20),line_color='r',show=False) p4=plot(besselj(3,x),(x,-20,20),line_color='c',show=False) p1.extend(p2) p1.extend(p3) p1.extend(p4) p1.show()
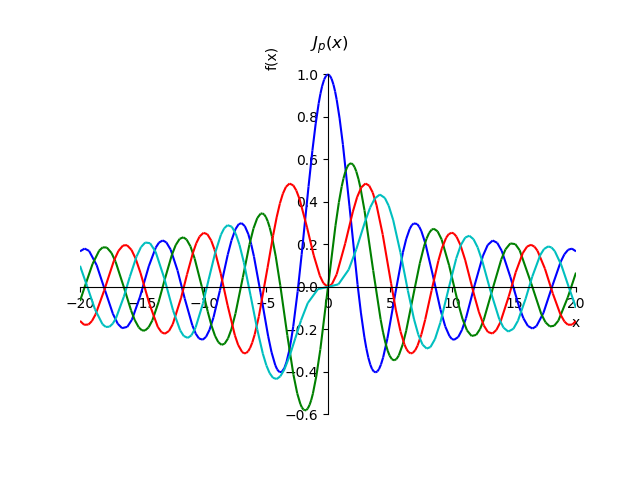
باستخدام العلاقة لمجموع سلسلة ، يمكننا إثبات خاصية هذه الوظائف لأوامر كاملة
J1(x)=−J−1(x):
خاصية Bessel وظيفة من النوع الأول from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1}(x)=-J_{-1}(x)" p1=plot(besselj(1,x),(x,-10,10),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(-1,x),(x,-10,10),line_color='r',show=False) p1.extend(p2) p1.show()

لإظهار ظروف كوشي ، نقوم ببناء وظيفة
J1/3(x) ومشتقاته
fracdJ1/3(x)dx: :
وظيفة ترتيب كسور ومشتقاتها from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1/3}(x),J{}'_{1/3}(x)" p1=plot(besselj(1/3,x),(x,-1,10),line_color='b',title=' $'+st+ '$',ylim=(-1,2),show=False) def dbesselj(p,x): return diff(summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]),x) p2=plot(dbesselj(1/3,x),(x,-1,10),line_color='g',show=False) p1.extend(p2) p1.show()
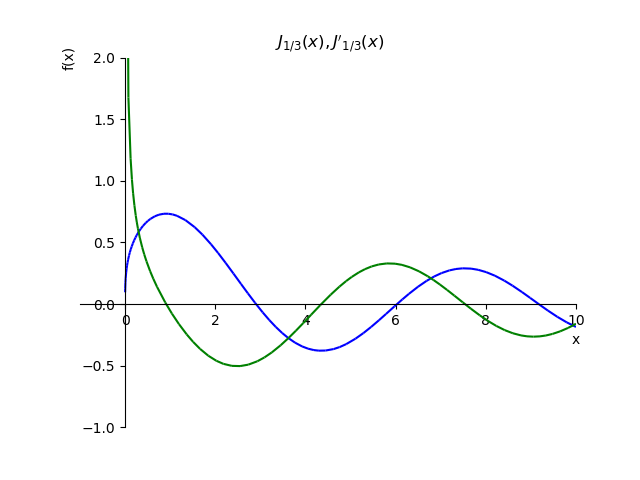
ومع ذلك ، بالنسبة للحسابات العملية ، يتم استخدام وحدة mpmath الرائعة ، والتي لا تسمح فقط بحل المعادلات عدديًا مع وظائف Bessel من النوع الأول والثاني ، بما في ذلك المعادلات المعدلة لجميع الطلبات المقبولة ، ولكن أيضًا بناء الرسوم البيانية مع القياس التلقائي.
بالإضافة إلى ذلك ، لا تتطلب وحدة mpmath أدوات خاصة لمشاركة الرياضيات الرمزية والرقمية. تاريخ إنشاء هذه الوحدة وإمكانية استخدامها لتحويل لابلاس معكوس سبق أن فكرت فيه في المنشور [2]. نواصل الآن مناقشة mpmath للعمل مع وظائف Bessel [3].
وظيفة بسل من النوع الأول JN(x)mpmath.besselj (n ، x ، مشتق = 0) - يعطي وظيفة Bessel من النوع الأول

. وظائف
JN(x) هو الحل للمعادلة التفاضلية التالية:
x2y″+xy′+(x2−n2)y=0
لكل إيجابي
ن يتصرف مثل الجيب أو جيب تمام ، مضروب بمعامل يتناقص ببطء مع
x rightarrow pm inftyوظيفة بسل من النوع الأول
JN(x) هي حالة خاصة من وظيفة hypergeometric
oF1 :
Jn(x)= fracxn2n Gamma(n+1)oF1(n+1، fracx24)
وظيفة بسل يمكن تمييزها
مدولا الأوقات بشرط ألا يكون مشتق mth يساوي الصفر:
fracdmdxmJn(x)
وظيفة بسل من النوع الأول
JN(x) لأوامر الأعداد الصحيحة الموجبة n = 0،1،2،3 - حل معادلة Bessel:
from mpmath import* j0 = lambda x: besselj(0,x) j1 = lambda x: besselj(1,x) j2 = lambda x: besselj(2,x) j3 = lambda x: besselj(3,x) plot([j0,j1,j2,j3],[0,14]

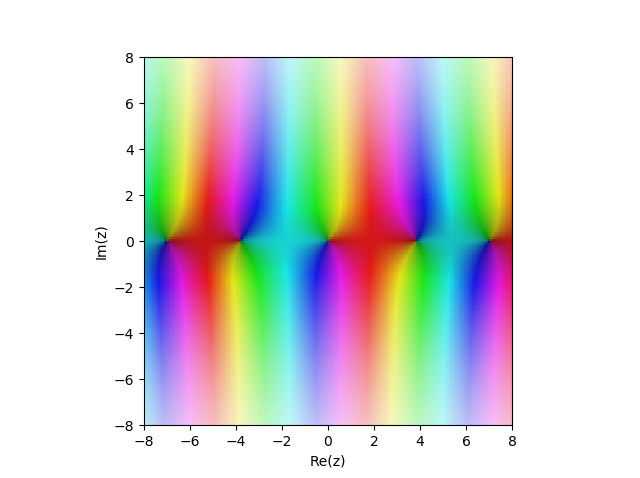
وظيفة بسل من النوع الأول
JN(x) في الطائرة المعقدة:
from sympy import* from mpmath import* cplot(lambda z: besselj(1,z), [-8,8], [-8,8], points=50000)
الأمثلة على ذلك:
وظيفة

يوفر نتيجة مع عدد معين من الأرقام
(mp.dps) بعد فاصلة:
from mpmath import* mp.dps = 15; mp.pretty = True print(besselj(2, 1000)) nprint(besselj(4, 0.75)) nprint(besselj(2, 1000j)) mp.dps = 25 nprint( besselj(0.75j, 3+4j)) mp.dps = 50 nprint( besselj(1, pi))
يمكن أن تكون وسيطة دالة عددًا كبيرًا:
from mpmath import* mp.dps = 25 nprint( besselj(0, 10000)) nprint(besselj(0, 10**10)) nprint(besselj(2, 10**100)) nprint( besselj(2, 10**5*j))
وظائف Bessel من النوع الأول ترضي التماثلات البسيطة فيما يتعلق
س=0دولا :
from sympy import* from mpmath import* mp.dps = 15 nprint([besselj(n,0) for n in range(5)]) nprint([besselj(n,pi) for n in range(5)]) nprint([besselj(n,-pi) for n in range(5)])
الجذور ليست دورية ، ولكن المسافة بين الجذور المتعاقبة تقترب بشكل متقارب
2π . وظائف Bessel من النوع الأول لها الكود التالي:
from mpmath import* print(quadosc(j0, [0, inf], period=2*pi)) print(quadosc(j1, [0, inf], period=2*pi))
ل
ن=1/2دولا أو
n=−1/2 يتم تقليل وظيفة Bessel إلى وظيفة مثلثية:
from sympy import* from mpmath import* x = 10 print(besselj(0.5, x)) print(sqrt(2/(pi*x))*sin(x)) print(besselj(-0.5, x)) print(sqrt(2/(pi*x))*cos(x))
يمكن حساب المشتقات من أي أمر ،
والأوامر السلبية تتوافق مع التكامل :
from mpmath import* mp.dps = 25 print(besselj(0, 7.5, 1)) print(diff(lambda x: besselj(0,x), 7.5)) print(besselj(0, 7.5, 10)) print(diff(lambda x: besselj(0,x), 7.5, 10)) print(besselj(0,7.5,-1) - besselj(0,3.5,-1)) print(quad(j0, [3.5, 7.5]))
التمايز بترتيب غير صحيح يعطي مشتق كسري بمعنى Riemann-Liouville التفاضلي المتكامل ، محسوب باستخدام الوظيفة
difint() :
from mpmath import* mp.dps = 15 print(besselj(1, 3.5, 0.75)) print(differint(lambda x: besselj(1, x), 3.5, 0.75))
طرق أخرى لاستدعاء وظيفة Bessel من النوع الأول من الصفر والأوامر الأولى
mpmath.j0 (x) - يحسب وظيفة Bessel
J0(x) ؛
mpmath.j1 (x) - يحسب وظيفة Bessel
J1(x) ؛
وظائف بسل من النوع الثانيbessely (n، x، مشتق = 0) يحسب دالة Bessel من النوع الثاني من العلاقة:
Yn(x)= fracJn(x)cos( pi cdotn)−J−n(x)sin( pi cdotn)
للحصول على عدد صحيح
ن يجب فهم الصيغة التالية على أنها الحد. وظيفة بسل يمكن تمييزها
مدولا الأوقات بشرط ألا يكون مشتق mth يساوي الصفر:
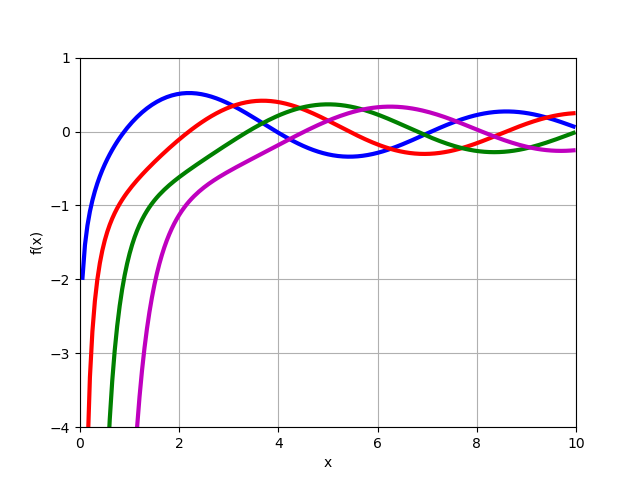
fracdmdxmYn(x)وظيفة بسل من النوع الثاني
Yn(x) لأوامر صحيح عدد صحيح
n=0،1،2،3 .
from sympy import* from mpmath import* y0 = lambda x: bessely(0,x) y1 = lambda x: bessely(1,x) y2 = lambda x: bessely(2,x) y3 = lambda x: bessely(3,x) plot([y0,y1,y2,y3],[0,10],[-4,1])
2nd نوع بسل وظيفة
Yn(x) في الطائرة المعقدة
from sympy import* from mpmath import* cplot(lambda z: bessely(1,z), [-8,8], [-8,8], points=50000)
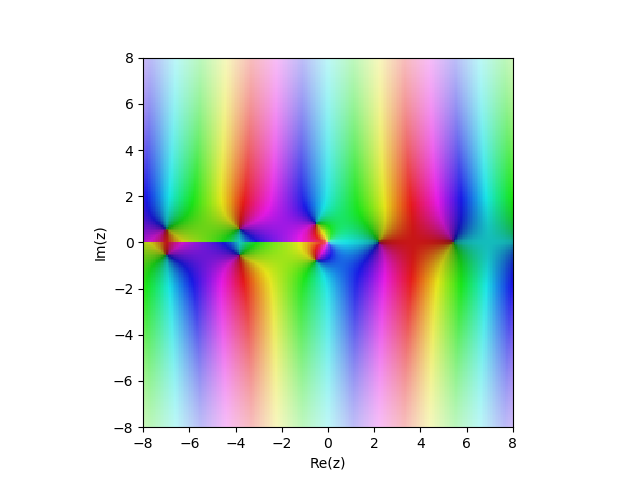
الأمثلة على ذلك:
بعض القيم الوظيفية
Yn(x) :
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0,0)) print(bessely(1,0)) print(bessely(2,0)) print(bessely(1, pi)) print(bessely(0.5, 3+4j))
يمكن أن تكون الحجج كبيرة:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0, 10000)) print(bessely(2.5, 10**50)) print(bessely(2.5, -10**50))
المشتقات من أي أمر ، بما في ذلك السلبية ، يمكن حسابها:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(2, 3.5, 1)) print(diff(lambda x: bessely(2, x), 3.5)) print(bessely(0.5, 3.5, 1)) print(diff(lambda x: bessely(0.5, x), 3.5)) print(diff(lambda x: bessely(2, x), 0.5, 10)) print(bessely(2, 0.5, 10)) print(bessely(2, 100.5, 100)) print(quad(lambda x: bessely(2,x), [1,3])) print(bessely(2,3,-1) - bessely(2,1,-1))
وظيفة بسل معدلة من النوع الأول
mpmath.besseli(n, x, derivative=0)
besseli (ن ، س ، مشتق = 0) تعديل وظيفة بسل من النوع الأول
In(x)= mathiti−nJn(ix)
fracdmdxmIn(x)
تعديل بسل وظيفة
In(x) لأوامر حقيقية
n=0،1،2،3 :
from mpmath import* i0 = lambda x: besseli(0,x) i1 = lambda x: besseli(1,x) i2 = lambda x: besseli(2,x) i3 = lambda x: besseli(3,x) plot([i0,i1,i2,i3],[0,5],[0,5])
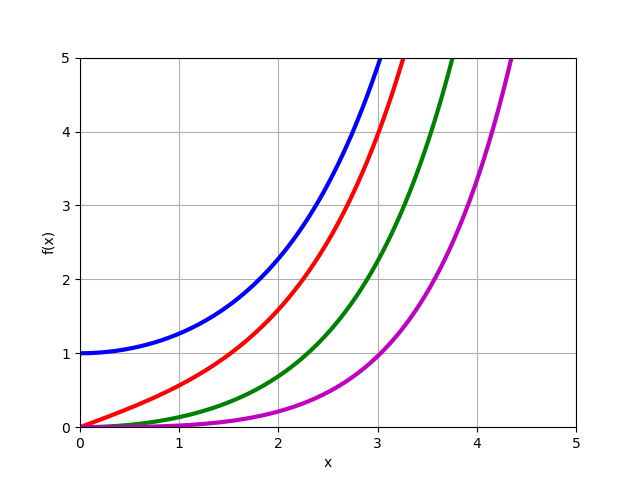
تعديل بسل وظيفة
In(x) في الطائرة المعقدة
from mpmath import* cplot(lambda z: besseli(1,z), [-8,8], [-8,8], points=50000)

الأمثلة على ذلك:
بعض المعاني
In(x) from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(0,0)) print(besseli(1,0)) print(besseli(0,1)) print(besseli(3.5, 2+3j))
يمكن أن تكون الحجج كبيرة:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 1000)) print(besseli(2, 10**10)) print(besseli(2, 6000+10000j))
بالنسبة للأعداد الصحيحة n ، يحمل التمثيل التكاملي التالي:
from mpmath import* mp.dps = 15; mp.pretty = True n = 3 x = 2.3 print(quad(lambda t: exp(x*cos(t))*cos(n*t), [0,pi])/pi) print(besseli(n,x))
يمكن حساب المشتقات من أي أمر:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 7.5, 1)) print(diff(lambda x: besseli(2,x), 7.5)) print(besseli(2, 7.5, 10)) print(diff(lambda x: besseli(2,x), 7.5, 10)) print(besseli(2,7.5,-1) - besseli(2,3.5,-1)) print(quad(lambda x: besseli(2,x), [3.5, 7.5]))
وظائف Bessel المعدلة من النوع الثاني ،
mpmath.besselk(n, x)
besselk (n، x) تم تعديل وظائف Bessel من النوع الثاني
Kn(x)= frac pi4 fracI−n(x)−In(x)sin( pi cdotn)
للحصول على عدد صحيح
ن يجب فهم هذه الصيغة كحد أقصى.
وظيفة Bessel المعدلة من النوع الثاني
Kn(x) للمواد
n=0،1،2،3 :
from mpmath import* k0 = lambda x: besselk(0,x) k1 = lambda x: besselk(1,x) k2 = lambda x: besselk(2,x) k3 = lambda x: besselk(3,x) plot([k0,k1,k2,k3],[0,8],[0,5])
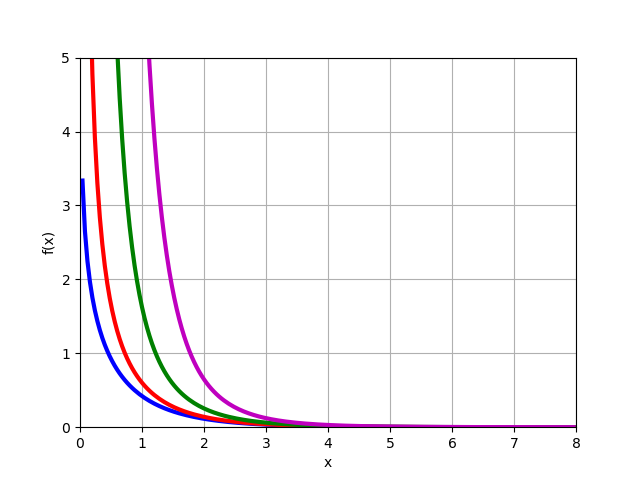
وظيفة Bessel المعدلة من النوع الثاني
Kn(x)) في الطائرة المعقدة
from mpmath import* cplot(lambda z: besselk(1,z), [-8,8], [-8,8], points=50000)
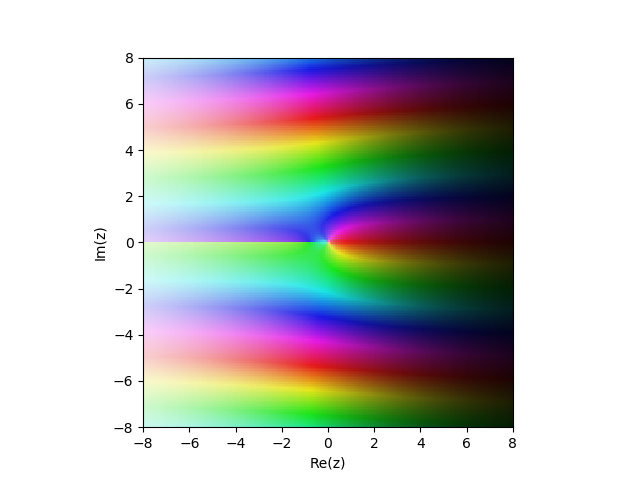
الأمثلة على ذلك:
الحجج المعقدة والمعقدة:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0,1)) print(besselk(0, -1)) print(besselk(3.5, 2+3j)) print(besselk(2+3j, 0.5))
الحجج هي أرقام كبيرة
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0, 100)) print(besselk(1, 10**6)) print(besselk(1, 10**6*j)) print(besselk(4.5, fmul(10**50, j, exact=True)))
ملامح سلوك وظيفة في نقطة ما
س=0دولا :
from mpmath import * print(besselk(0,0)) print(besselk(1,0)) for n in range(-4, 5): print(besselk(n, '1e-1000'))
Bessel Function Zeros besseljzero() mpmath.besseljzero(v, m, derivative=0)
لأمر حقيقي
mathit nu geq0 و عدد صحيح موجب
مدولا عوائد
j nu،m ، الصفر الإيجابي لمهمة بسل من النوع الأول
J nu(ض) (انظر
besselj () ). بدلا من ذلك ، مع

يعطي أول صفر سلبي صفر
j′ nu،m من
J′ nu(z) . فهرسة تسميات الاتفاقيات باستخدام Abramowitz & Stegun و DLMF. إيلاء الاهتمام لحالة خاصة.
j′0،1=0 في حين أن جميع الأصفار الأخرى إيجابية.
في الواقع ، يتم حساب الأصفار البسيطة فقط (جميع الأصفار في وظائف Bessel بسيطة ، ما عدا متى
z=0 ) ، و
j nu،m يصبح وظيفة رتابة من
nu و
مدولا . تتناوب الأصفار وفقًا لعدم المساواة:
j′ nu،k<j nu،k<j′ nu،k+1
j nu،1<j nu+1،2<j nu،2<j nu+1،2<j nu،3 cdots
الأمثلة على ذلك:
يؤدي الأصفار من وظائف بسل
J0(z) .
J1(z) .
J2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1)) print(besseljzero(0,2)) print(besseljzero(0,3)) print(besseljzero(1,1)) print(besseljzero(1,2)) print(besseljzero(1,3)) print(besseljzero(2,1)) print(besseljzero(2,2)) print(besseljzero(2,3))
الأصفار الرائدة لمشتقات Bessel
J′0(z) .
J′1(z) .
J′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1,1)) print(besseljzero(0,2,1)) print(besseljzero(0,3,1)) print(besseljzero(1,1,1)) print(besseljzero(1,2,1)) print(besseljzero(1,3,1)) print(besseljzero(2,1,1)) print(besseljzero(2,2,1)) print(besseljzero(2,3,1))
الأصفار مع مؤشر كبير:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,100)) print(besseljzero(0,1000)) print(besseljzero(0,10000)) print(besseljzero(5,100)) print(besseljzero(5,1000)) print(besseljzero(5,10000)) print(besseljzero(0,100,1)) print(besseljzero(0,1000,1)) print(besseljzero(0,10000,1))
الأصفار من الوظائف مع ترتيب كبير:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(50,1)) print(besseljzero(50,2)) print(besseljzero(50,100)) print(besseljzero(50,1,1)) print(besseljzero(50,2,1)) print(besseljzero(50,100,1))
الأصفار من الوظائف مع ترتيب كسري:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0.5,1)) print(besseljzero(1.5,1)) print(besseljzero(2.25,4))
و
J nu(ض) . و
J′ nu(z) يمكن التعبير عنها كمنتجات لا حصر لها في أصفارها:
from mpmath import * mp.dps = 6; mp.pretty = True v,z = 2, mpf(1) nprint((z/2)**v/gamma(v+1) * \ nprod(lambda k: 1-(z/besseljzero(v,k))**2, [1,inf])) print(besselj(v,z)) nprint((z/2)**(v-1)/2/gamma(v) * \ nprod(lambda k: 1-(z/besseljzero(v,k,1))**2, [1,inf])) print(besselj(v,z,1))
besselyzero() mpmath.besselyzero(v, m, derivative=0)
لأمر حقيقي
mathit nu geq0 و عدد صحيح موجب
مدولا عوائد
y nu،m .
مدولا ، صفر إيجابي من النوع الثاني من وظيفة بسل
Y nu(z) (انظر
Bessely () ). بدلا من ذلك ، مع

يعطي أول صفر إيجابي
y′ nu،m من
Y′ nu(z) . تتناوب الأصفار وفقًا لعدم المساواة:
y nu،k<y′ nu،k<y nu،k+1
y nu،1<y nu+1،2<y nu،2<y nu+1،2<y nu،3 cdots
الأمثلة على ذلك:
يؤدي الأصفار من وظائف بسل
Y0(z) .
Y1(z) .
Y2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1)) print(besselyzero(0,2)) print(besselyzero(0,3)) print(besselyzero(1,1)) print(besselyzero(1,2)) print(besselyzero(1,3)) print(besselyzero(2,1)) print(besselyzero(2,2)) print(besselyzero(2,3))
الأصفار الرائدة لمشتقات Bessel
Y′0(z) .
Y′1(z) .
Y′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1,1)) print(besselyzero(0,2,1)) print(besselyzero(0,3,1)) print(besselyzero(1,1,1)) print(besselyzero(1,2,1)) print(besselyzero(1,3,1)) print(besselyzero(2,1,1)) print(besselyzero(2,2,1)) print(besselyzero(2,3,1))
الأصفار مع مؤشر كبير:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,100)) print(besselyzero(0,1000)) print(besselyzero(0,10000)) print(besselyzero(5,100)) print(besselyzero(5,1000)) print(besselyzero(5,10000)) print(besselyzero(0,100,1)) print(besselyzero(0,1000,1)) print(besselyzero(0,10000,1))
الأصفار من الوظائف مع ترتيب كبير:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(50,1)) print(besselyzero(50,2)) print(besselyzero(50,100)) print(besselyzero(50,1,1)) print(besselyzero(50,2,1)) print(besselyzero(50,100,1))
الأصفار من الوظائف مع ترتيب كسري:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0.5,1)) print(besselyzero(1.5,1)) print(besselyzero(2.25,4))
بسل وظيفة التطبيقاتلا ترجع أهمية وظائف Bessel إلى الظهور المتكرر لمعادلة Bessel في التطبيقات ، ولكن أيضًا إلى حقيقة أنه يمكن التعبير عن حلول العديد من المعادلات التفاضلية الخطية من الدرجة الثانية الأخرى من حيث وظائف Bessel. لنرى كيف تظهر ، نبدأ معادلة بسل للنظام
ع في شكل:
z2 fracd2wdz2+z fracdwdz+(z2−p2)w=0،(1)دولا
والبديل هنا
w=x− alpha،z=kx beta،(2)
ثم ، باستخدام (2) وإدخال الثوابت
A،B،C من المعادلة (1) ، نحصل على:
x2y″+Axey′+(B+Cxq)y=0،(3)
A=1−2 alpha،B= alpha2− beta2p2،C= beta2k2،q=2 beta،(4)دولا
من المعادلة (4) نحصل على:
\ left \ {\ start {matrix} \ alpha = \ frac {1-A} {2} ، \\ \ beta = \ frac {q} {2} ، \\ k = \ frac {2 \ sqrt {C }} {q} \\ p = \ frac {\ sqrt {(1-A ^ {2} -4B}} {q} \\ \ end {matrix} \ right. (5)
إذا
C>0 .
q neq0 .
(1−A)2 geqslant4B ، ثم الحل العام (ل
x>0 ) من المعادلة (3) على النحو التالي:
y(x)=x alpha left[c1Jp(kx beta)+c2J−p(kx beta) الحق](6)دولا
حيث:
alpha .
beta .
ك يتم تحديدها من النظام (5). إذا
ع هو عدد صحيح بعد ذلك
Jp تحتاج إلى استبداله
Yp .
الانحناء الطولي للعمود الرأسينحن الآن نعتبر مهمة مهمة للتطبيقات العملية. في هذه المهمة ، يجب تحديد وقت ثني عمود رأسي موحد تحت ثقله. نحن نفترض
س=0دولا في الطرف العلوي الحر من العمود و
x=L>0 في قاعدتها ؛ نحن نفترض أن القاعدة يتم إدخالها بشكل صارم (أي بدون حراك ثابت) في القاعدة (في الأرض) ، وربما في الخرسانة.
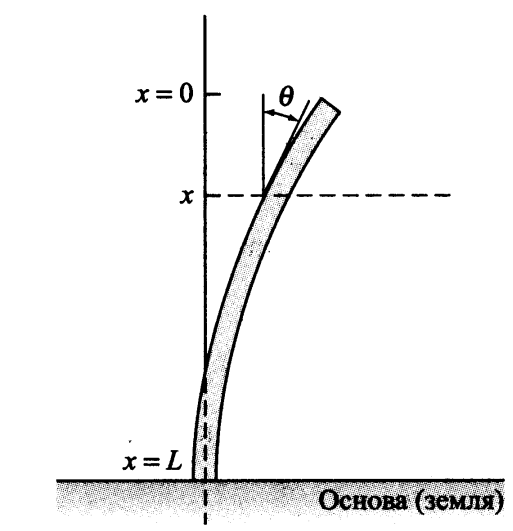
تشير إلى الانحراف الزاوي للعمود في هذه النقطة
x من خلال
theta(x) . من نظرية المرونة في ظل هذه الظروف ، يتبع ذلك:
EI fracd2 thetadx2+g rhox theta=0،(7)
اين
E - معامل يونغ للمادة العمود ،
I - لحظة الجمود في المقطع العرضي لها ،
rho - الكثافة الخطية للعمود و
g - تسارع الجاذبية. شروط الحدود من النموذج:
theta′(0)=0، theta(L)=0،(8)
سنقوم بحل المشكلة باستخدام (7) و (8) مع:
lambda= gamma2= fracg rhoEI(9)
نعيد كتابة (7) مع مراعاة (9) تحت شرط (8):
fracd2 thetadx2+ gamma2x theta=0؛ fracd thetadx=0، theta(L)=0.(10)
يمكن تشويه العمود فقط إذا كان هناك حل غير تافه للمشكلة (10) ؛ بخلاف ذلك ، سيبقى العمود في وضع لا ينحرف عن العمودي (بمعنى أنه غير قادر جسديًا على الانحراف عن العمودي).
المعادلة التفاضلية (10) هي معادلة Airy. المعادلة (10) لها شكل المعادلة (3) لـ
أ=ب=0دولا .
C= gamma2 .

. من نظام المعادلات (5) نحصل عليها
alpha= frac12 .
beta= frac32 .
k= frac23 gamma .
p= frac13 .
لذلك ، الحل العام لديه الشكل:
theta(x)=x1/2 left[c1J1/3( frac23 gammax3/2)+c2J−1/3( frac23 gammax3/2) right].(11)دولا
لتطبيق الشروط الأولية ، نحن بديل
p= pm frac13 في
Jp= sum inftym=0 frac(−1)mm! Gamma(p+m+1) left( fracx2 right)2m+p(12)
بعد التحويل (12) ، مع الأخذ في الاعتبار الحل (11) ، نحصل على:
theta(x)= fracc1 gamma1/331/3 Gamma(4/3) left(x− frac gamma2x412+ frac gamma4x7504− cdot cdot cdot right)++ fracc231/3 gamma1/3 Gamma( frac23) left(1− frac gamma2x36+ frac gamma4x6180− cdot cdot cdot right).(13)
المقدمة عند نقطة البداية
theta′(0)=0 نحن نحصل عليها
c1=0 ، ثم (11) يأخذ النموذج:
theta(x)=c2x1/2J−1/3( frac23 gammax3/2)،(14)
المقدمة في نقطة النهاية
theta(L)=0 ، من (14) نحصل على:
J−1/3( frac23 gammaL3/2)=0(15)
تجدر الإشارة إلى أنه لا يمكن إجراء التحويلات (13) ، (14) إذا تم إنشاء الرسوم البيانية للوظائف
J1/3(x)،J−1/3(x) باستخدام القدرات المدروسة لوحدة mpmath:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) f1=lambda x: besselj(1/3,x) plot([f,f1], [0, 15])
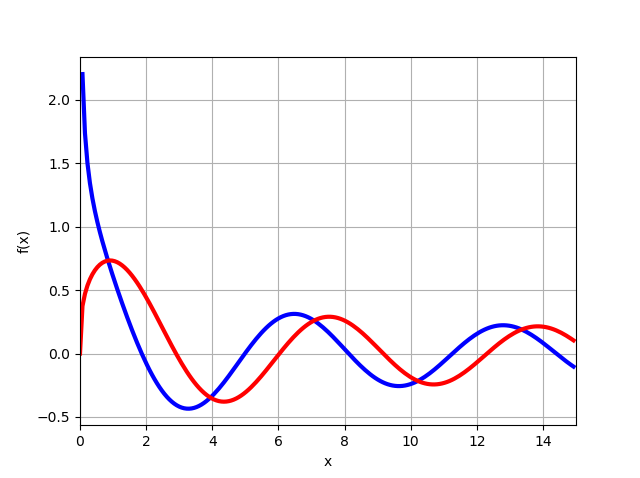
من الرسم البياني ، تتبع الدالة x = 0
J1/3(0)=0 مع الأخذ بعين الاعتبار الحل (11) ، نحصل على الفور على المعادلة الضرورية (15) ، يبقى فقط لإيجاد z ، كما هو مبين أدناه.
وبالتالي ، يتم تشويه العمود فقط إذا
z= frac23 gammaL3/2 هو أصل المعادلة
J−1/3(z)=0 . بناء وظيفة
J−1/3(z) على مخطط منفصل:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) plot(f, [0, 15])

يوضح الرسم البياني أن الجذر الأول أقل بقليل من 2. ابحث عن الجذر
z من المعادلة
J−1/3(z)=0 يمكنك ، باستخدام
دالة findroot (f ، z0) ، قبول نقطة البحث وفقًا للرسم البياني
x0=1دولا وستة منازل عشرية
mp.dps = 6 :
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) print("z0=%s"%findroot(f, 1)
نحصل على:

نحسب الطول الحرج ، على سبيل المثال ، سارية العلم ، باستخدام الصيغة (15):
ارتفاع سارية العلم لمعلمات مختلفة في القسم from numpy import* def LRr(R,r): E=2.9*10**11
نحصل على:
8.47 م
10.25 م
قد يكون سارية العلم المجوفة أعلى من سارية العلم.
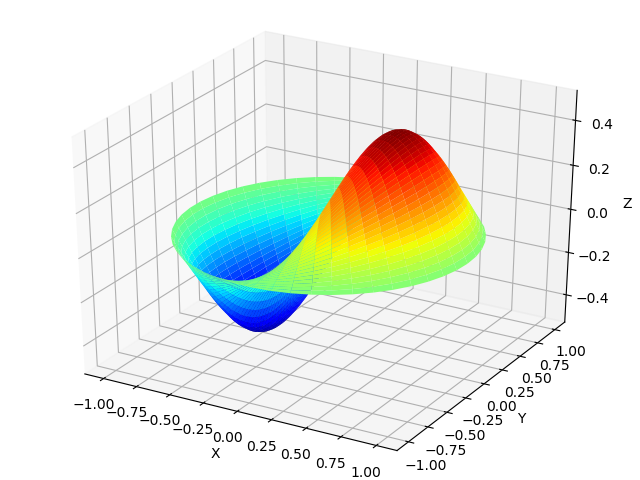
انتشار الموجة في غشاء رقيق.
غشاء رقيق عندما تدخل الموجات الصوتية لا يتذبذب فقط مع تردد الأمواج. يمكن الحصول على شكل اهتزازات الغشاء في وظائف Bessel وفقًا للقائمة التالية ، وذلك باستخدام الصيغ
besselj () و
besseljzero () :
غشاء الموجي from mpmath import* from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm def Membrana(r): mp.dps=25 return cos(0.5) * cos( theta) *float(besselj(1,r*besseljzero(1,1) ,0)) theta =linspace(0,2*pi,50) radius = linspace(0,1,50) x = array([r * cos(theta) for r in radius]) y = array([r * sin(theta) for r in radius]) z = array([Membrana(r) for r in radius]) fig = plt.figure("") ax = Axes3D(fig) ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_zlabel('Z') plt.show()
بديل لوحدة mpmath في وظائف Bessel الخاصة بمكتبة SciPy
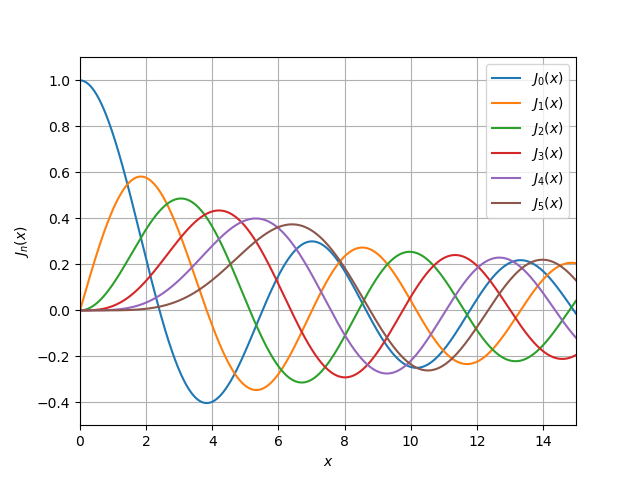
دون الخوض في مناقشة مفصلة لوظائف Bessel من مكتبة SciPy [4] ، سأقدم فقط قائمتين للتخطيط لوظائف
jv (v ، x) ، النوع الأول والثاني ،
yv (v ، x) :
jv (v ، x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.jv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$J_{0}(x)$', '$ J_{1}(x)$', '$J_{2}(x)$', '$J_{3}(x)$', '$ J_{4}(x)$','$ J_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('${J}_n(x)$') py.grid(True) py.show()
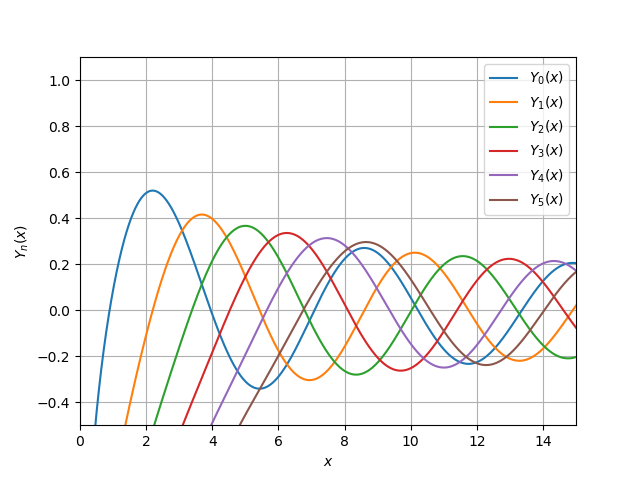
yv (v ، x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.yv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$Y_{0}(x)$', '$ Y_{1}(x)$', '$Y_{2}(x)$', '$Y_{3}(x)$', '$ Y_{4}(x)$','$ Y_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('$Y_{n}(x)$') py.grid(True) py.show()
الاستنتاجات:
توضح المقالة أساسيات العمل مع وظائف Bessel باستخدام مكتبات mpmath و sympy و scipy ، وتقدم أمثلة على استخدام الدالات لحل المعادلات التفاضلية. قد تكون المادة مفيدة في دراسة معادلات الفيزياء الرياضية.
المراجع:
1.
وظائف بسل2.
استخدام تحويل لابلاس العكسي لتحليل الروابط الديناميكية لأنظمة التحكم3.
وظيفة بسل الوظائف ذات الصلة4.
وظائف خاصة (scipy.special).