يعد تحويل النماذج أثناء الطيران ممارسة شائعة في محاكاة فيزياء التشوهات ، وكذلك في الألعاب ذات المحتوى الذي يتم إنشاؤه ديناميكيًا وقابل للتعديل. في مثل هذه الحالات ، من المريح تطبيق أساليب التحرير الإجرائي وإنشاء الهندسة. غالباً ما تسمح هذه الأخيرة بحفظ البايتات العزيزة عند نقل البيانات التي تم تنزيلها من الشبكة. بالاضافة الى ذلك ، انها متعة!
يهدف المقال إلى ضخ مهارات المعالجة الإجرائية للشبكات في الوحدة. سنتحدث عن عمليات تحويل وتوليد أجزاء من الشبكة.

تتضمن مجموعة أدواتنا للتحرير الإجرائي للنماذج ثلاثية الأبعاد ثلاث عمليات أساسية: التثليث ، وحركة النقاط ، والبثق. سنتحدث بالتفصيل عن آخر اثنين. أولاً ، ضع في اعتبارك أبسط عمليات الحركة - تحريك الرؤوس ، وتدوير الحواف والمثلثات. ثم سنتعامل مع واحدة من الطرق لتوليد هندسة جديدة - عملية البثق.
في منشور سابق ، وصفنا هيكلنا للعمل المريح مع البيانات من النماذج ثلاثية الأبعاد.كود الهيكلpublic static class CustomMeshPool { private static List<CustomMesh> Pool; private static int pointer; public static CustomMesh GetMesh(int id) { return Pool[id]; } public static int Push(CustomMesh customMesh) { if (Pool == null) Pool = new List<CustomMesh>(); pointer = GetAvailableIndex(); if (pointer < Pool.Count) Pool[pointer] = customMesh; else Pool.Add(customMesh); return pointer; } public static bool Remove(int index) { if (Pool == null) return false; var b = Pool[index] == null; Pool[index] = null; return b; } public static int GetAvailableIndex() { if (Pool == null) return 0; var availableIndex = Pool.FindIndex(mesh => mesh == null); return availableIndex != -1 ? availableIndex : Pool.Count; } public static void Flush() { if (Pool != null) Pool.Clear(); } } public class CustomMesh { public int Id; public Triangle[] Triangles; public Vector3[] vertices; public Vector3[] normals; public Vector2[] uv0, uv2; public Color[] colors; public CustomMesh(Vector3[] vertices, int[] triangles, Vector3[] normals, Vector2[] uv0, Vector2[] uv2, Color[] colors) { this.vertices = vertices; this.normals = normals; if (normals != null) for (var i = 0; i < this.normals.Length; i++) { this.normals[i] = this.normals[i].normalized; } this.uv0 = uv0; this.uv2 = uv2; this.colors = colors; var ptr = CustomMeshPool.GetAvailableIndex(); CustomMeshPool.Push(this); Id = ptr; Triangles = new Triangle[triangles.Length / 3]; Triangles = Triangles .AsParallel() .Select((t, i) => new Triangle(ptr, i, triangles[i * 3], triangles[i * 3 + 1], triangles[i * 3 + 2])) .ToArray(); } } public struct Triangle { private int _index; public int Index { get { return _index; } set { _index = value; if (_edges != null) { _edges[0].TriangleIndex = value; _edges[1].TriangleIndex = value; _edges[2].TriangleIndex = value; } } } private int _meshId; public int MeshId { get { return _meshId; } internal set { _meshId = value; } } private Edge[] _edges; public Edge[] Edges { get { return _edges; } set { if (value.Length == 3) { _edges = value; for (var i = 0; i < 3; i++) { _edges[i].TriangleIndex = _index; } } else throw new IndexOutOfRangeException(); } } public Vertex V0 { get { return Edges[0].v0; } set { if (value.MeshId != MeshId) throw new Exception("Not the same mesh"); Edges[0].v0 = value; Edges[2].v1 = value; } } public Vertex V1 { get { return Edges[1].v0; } set { if (value.MeshId != MeshId) throw new Exception("Not the same mesh"); Edges[1].v0 = value; Edges[0].v1 = value; } } public Vertex V2 { get { return Edges[2].v0; } set { if (value.MeshId != MeshId) throw new Exception("Not the same mesh"); Edges[2].v0 = value; Edges[1].v1 = value; } } public Triangle(int meshId, int index, int v0, int v1, int v2) { _index = index; _meshId = meshId; var edges = new Edge[3]; edges[0] = new Edge(meshId, index, v0, v1); edges[1] = new Edge(meshId, index, v1, v2); edges[2] = new Edge(meshId, index, v2, v0); _edges = edges; } } public struct Edge { public Vertex v0; public Vertex v1; private int _meshId; public int MeshId { get { return _meshId; } internal set { _meshId = value; } } private int _triangleIndex; public int TriangleIndex { get { return _triangleIndex; } internal set { _triangleIndex = value; } } public Edge(int meshId, int triangleIndex, int v0Index, int v1Index) { _meshId = meshId; _triangleIndex = triangleIndex; v0 = new Vertex() { MeshId = meshId, Index = v0Index }; v1 = new Vertex() { MeshId = meshId, Index = v1Index }; } } public struct Vertex { public int Index; private int _meshId; public int MeshId { get { return _meshId; } internal set { _meshId = value; } } public Vector3 position { get { return CustomMeshPool.GetMesh(_meshId).vertices[Index]; } set { CustomMeshPool.GetMesh(_meshId).vertices[Index] = value; } } public Vector3 normal { get { return CustomMeshPool.GetMesh(_meshId).normals[Index]; } set { CustomMeshPool.GetMesh(_meshId).normals[Index] = value; } } public Vector2 uv0 { get { return CustomMeshPool.GetMesh(_meshId).uv0[Index]; } set { CustomMeshPool.GetMesh(_meshId).uv0[Index] = value; } } public Vector2 uv2 { get { return CustomMeshPool.GetMesh(_meshId).uv2[Index]; } set { CustomMeshPool.GetMesh(_meshId).uv2[Index] = value; } } public Color color { get { return CustomMeshPool.GetMesh(_meshId).colors[Index]; } set { CustomMeshPool.GetMesh(_meshId).colors[Index] = value; } } }
كما ترون ، يتم استخدام PLINQ هنا. وذلك لأن خوارزميات الهندسة الحاسوبية يمكن تحسينها غالبًا من خلال تعدد مؤشرات الترابط.
بالطبع ، يتم إنشاء المزيد من تصميمات LINQ أثناء تنفيذ تصميمات LINQ أكثر من تنفيذ الرمز "اليدوي". ومع ذلك ، يتم تعويض هذا العيب إلى حد كبير باختصار مثل هذه التصميمات ، وكذلك وجود أدوات إدارة الموارد المضمنة في PLINQ. بالإضافة إلى ذلك ، يتم تنفيذ الانتقال بين تطبيقات أحادية الربط ومتعددة مؤشرات الترابط بأمر واحد فقط ، مما يسهل عملية التصحيح إلى حد كبير.تطور ، تطور ، أريد أن أربك
ننتقل إلى عمليات الحركة. لا يوجد شيء معقد حول تحريك القمم. فقط لا تنسى قمم الذروة: إذا لزم الأمر ، يجب أن يتغير وضعهم أيضًا.
يتم تنفيذ الخوارزمية عن طريق إضافة متجه الحركة إلى وضع قمة الرأس. يحدث التحول بالنسبة إلى أصل النموذج (
المحور ). تجدر الإشارة إلى أن موقف المضلعات أثناء هذه التحولات يمكن أن يتغير ، لكن الحالة الطبيعية لرؤوسها لا يمكن أن تتغير. ومع ذلك ، لتبسيط العرض التقديمي ، لن نفكر في هذا الفارق الدقيق.
أدوات CAD لها وظيفة لإعادة حساب القواعد الطبيعية ، والتي يتم استدعاؤها عادة بعد تطبيق التحولات المطلوبة. هناك طرق مختلفة للقيام بهذا التخصيص. يحسب الأكثر شيوعًا المستوى العادي لمستوى كل مثلث ، ثم يعين عاديًا لكل رأس مثل متوسط الحالة الطبيعية للمثلثات التي ينتمي إليها هذا الرأس.بشكل عام ، لا يوجد سبب وجيه لتعقيد الكود وتطبيق مصفوفة التحويل. تتوافق نتيجة إضافة ناقل حركة إلى موضع الرأس مع فكرة بديهية لحركته.
سرد طرق لتحريك قمة واحدة public struct Vertex { ... public void Translate(Vector3 movement, bool withCoincident = false) { var newPosition = position + movement; if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var mask = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(position); for (int i = 0; i < vertices.Length; i++) if (mask[i]) vertices[i] = newPosition; } else { position = newPosition; } } } public class CustomMesh { … public bool[] GetVerticesInPosition(Vector3 position) { bool[] buffer = new bool[vertices.Length]; for (int i = 0; i < buffer.Length; i++) { buffer[i] = Mathf.Abs(position.x - vertices[i].x) < Mathf.Epsilon && Mathf.Abs(position.y - vertices[i].y) < Mathf.Epsilon && Mathf.Abs(position.z - vertices[i].z) < Mathf.Epsilon; } return buffer; } }
يتم تنفيذ حركة الحواف والمثلثات بنفس الطريقة - عن طريق إضافة ناقل الإزاحة.
سرد طرق لتحريك المثلثات والحواف public struct Edge { … public void Translate(Vector3 movement, bool withCoincident = false) { if (withCoincident) { var vertices = CustomMeshPool.GetMesh(MeshId).vertices; var newV0Position = v0.position + movement; var newV1Position = v1.position + movement; var maskV0 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v0.position); var maskV1 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v1.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; } } else { v0.Translate(movement); v1.Translate(movement); } } } public struct Triangle { … public void Translate(Vector3 movement, bool withCoincident = false) { if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var newV0Position = V0.position + movement; var newV1Position = V1.position + movement; var newV2Position = V2.position + movement; var maskV0 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V0.position); var maskV1 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V1.position); var maskV2 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V2.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; else if (maskV2[i]) vertices[i] = newV2Position; } } else { V0.Translate(movement); V1.Translate(movement); V2.Translate(movement); } } }
لكن الأمر أكثر ملاءمة للتدوير والحجم باستخدام
مصفوفة التحول . من المحتمل ألا تكون نتيجة إجراء هذه العمليات بالنسبة إلى أصل إحداثيات النموذج هي ما كنت تتوقعه أو تريد رؤيته. عادة ما يتم اعتبار النقطة المرجعية للدوران والقياس في منتصف الكائن - باعتبارها النقطة الأكثر قابلية للفهم بالنسبة للبشر.
سرد طرق تدوير المثلثات والحواف public struct Edge { … public void Rotate(Quaternion rotation, bool withCoincident = false) { var pivot = (v0.position + v1.position) * 0.5f; var matrix = Matrix4x4.TRS(pivot, rotation, Vector3.one); var newV0Position = matrix.MultiplyPoint(v0.position - pivot); var newV1Position = matrix.MultiplyPoint(v1.position - pivot); if (withCoincident) { var vertices = CustomMeshPool.GetMesh(MeshId).vertices; var maskV0 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v0.position); var maskV1 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v1.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; } } else { v0.position = newV0Position; v1.position = newV1Position; } } public void Scale(Vector3 scale, bool withCoincident = false) { var pivot = (v0.position + v1.position) * 0.5f; var matrix = Matrix4x4.TRS(pivot, Quaternion.identity, scale); var newV0Position = matrix.MultiplyPoint(v0.position - pivot); var newV1Position = matrix.MultiplyPoint(v1.position - pivot); if (withCoincident) { var vertices = CustomMeshPool.GetMesh(MeshId).vertices; var maskV0 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v0.position); var maskV1 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v1.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; } } else { v0.position = newV0Position; v1.position = newV1Position; } } } public struct Triangle { … public void Rotate(Quaternion rotation, bool withCoincident = false) { var pivot = (V0.position + V1.position + V2.position) / 3; var matrix = Matrix4x4.TRS(Vector3.zero, rotation, Vector3.one); var newV0Position = matrix.MultiplyPoint(V0.position - pivot) + pivot; var newV1Position = matrix.MultiplyPoint(V1.position - pivot) + pivot; var newV2Position = matrix.MultiplyPoint(V2.position - pivot) + pivot; if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var maskV0 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V0.position); var maskV1 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V1.position); var maskV2 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V2.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; else if (maskV2[i]) vertices[i] = newV2Position; } } else { Edges[0].v0.position = newV0Position; Edges[1].v0.position = newV1Position; Edges[2].v0.position = newV2Position; } Edges[0].v0.normal = matrix.MultiplyPoint(V0.normal); Edges[1].v0.normal = matrix.MultiplyPoint(V1.normal); Edges[2].v0.normal = matrix.MultiplyPoint(V2.normal); } public void Scale(Vector3 scale, bool withCoincident = false) { var pivot = (V0.position + V1.position + V2.position) / 3; var matrix = Matrix4x4.TRS(pivot, Quaternion.identity, scale); var newV0Position = matrix.MultiplyPoint(V0.position - pivot); var newV1Position = matrix.MultiplyPoint(V1.position - pivot); var newV2Position = matrix.MultiplyPoint(V2.position - pivot); if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var maskV0 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V0.position); var maskV1 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V1.position); var maskV2 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V2.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; else if (maskV2[i]) vertices[i] = newV2Position; } } else { Edges[0].v0.position = newV0Position; Edges[1].v0.position = newV1Position; Edges[2].v0.position = newV2Position; } } }
سرب ثقب أنيق لأنفسنا
في النماذج ثلاثية الأبعاد ، يتم استخدام عملية البثق. لتنفيذه ، يجب أن يكون ناقل الحركة (الإزاحة) ومجموعة المضلعات معروفين. يمكن تقسيم عملية البثق إلى خطوتين:
1. إزاحة المضلعات بواسطة ناقل حركة محدد (
إزاحة ). في هذه الحالة ، من الضروري تكرار القمم التي تفصلها المضلعات الحدودية حتى لا تزعج موضع تلك العناصر التي لا تنتمي إلى الجزء النازح. وبعبارة أخرى ، تحتاج إلى المسيل للدموع وتحريك القطعة المحددة. إذا اكتملت هذه الخطوة أولاً ، فمن المحتمل أن ينقسم النموذج إلى أجزاء سيتعين ضمها في المستقبل.
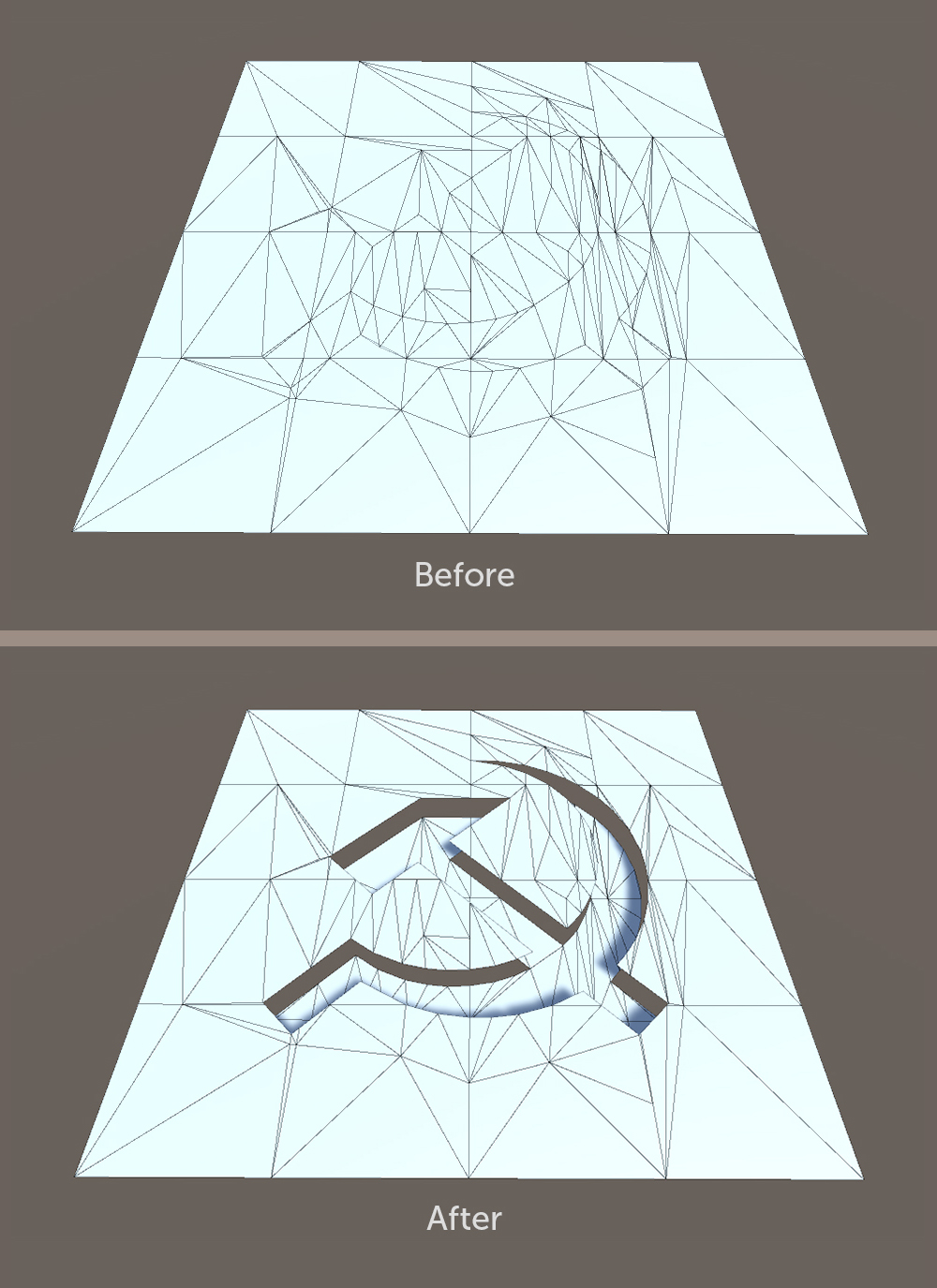
2. إضافة هندسة جديدة بين حدود الجزء المشرد والحدود التي تشكلت أثناء البثق. تمتلئ الفجوة بين الأجزاء الرئيسية والأجزاء المتحركة من النموذج بمضلعات تشكل جدارًا.
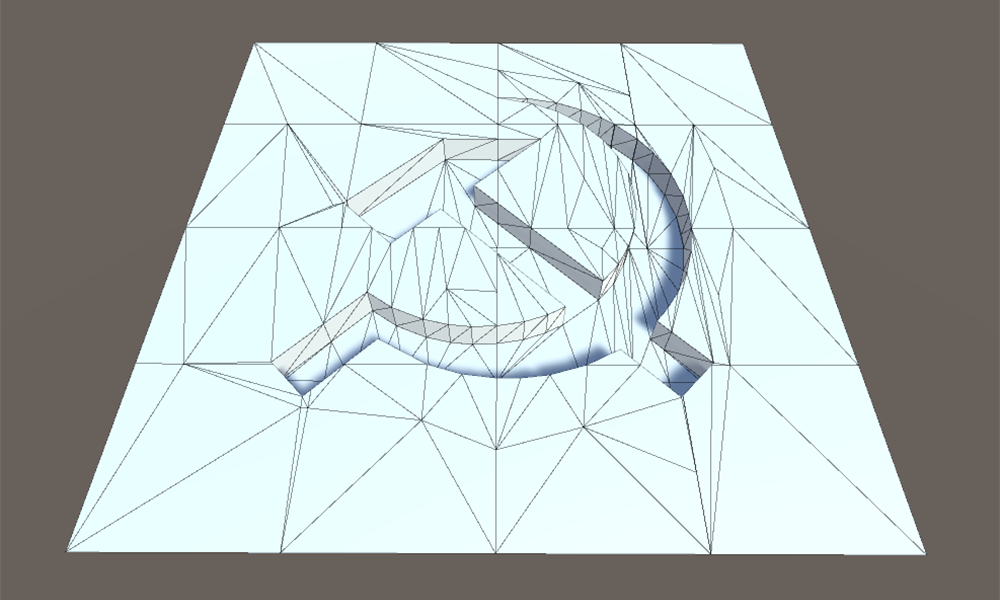
في التطبيق ، من الملائم أكثر بناء الجدار أولاً ، لأنه قبل التحول ، لدينا الوضع الأولي للحواف على الحدود ويمكننا استخدام هذه البيانات على الفور. خلاف ذلك ، سيكون عليك إما عكس اتجاه متجه القص أو حفظ بعض المعلومات حول الحالة الأولية للشبكة.
يتكون النموذج وأجزائه التي نتعامل معها من مجموعات من المضلعات المتجاورة الزوجية (مثلثات). نحن نسمي كل مجموعة من هذه
المجموعة .
 مجموعتان مخصصتان في Blender
مجموعتان مخصصتان في Blender
أولاً ، نحتاج إلى الحصول على جميع أطراف الخطوط التي تربط المجموعات المحددة. للقيام بذلك ، ما عليك سوى إضافة الحواف إلى القائمة بالتسلسل. إذا تم العثور على حافة مطابقة ، فيجب إزالتها دون إضافة الحافة الحالية. من أجل التشغيل الصحيح لهذه الخوارزمية ، من الضروري إدخال قيود: على مجموعة المثلثات المحددة ، لا يوجد أكثر من حدين متزامنين. في الحالات التي
يتم فيها استخدام
Extrude ، تفي النماذج غالبًا بهذا الشرط ، وتتطلب الخوارزمية الأكثر تعقيدًا موارد حسابية كبيرة.
سرد طرق للحصول على حواف تنتمي إلى معالم internal static class LinkedListExtension { internal static IEnumerable<LinkedListNode<T>> Nodes<T>(this LinkedList<T> list) { for (var node = list.First; node != null; node = node.Next) { yield return node; } } } public struct Vertex { … public bool IsInPosition(Vector3 other) { return Mathf.Abs(position.x - other.x) < Mathf.Epsilon && Mathf.Abs(position.y - other.y) < Mathf.Epsilon && Mathf.Abs(position.z - other.z) < Mathf.Epsilon; } } public struct Edge { … public bool Coincides(Edge other, bool includeDirection = false) { return v0.IsInPosition(other.v0.position) && v1.IsInPosition(other.v1.position) || !includeDirection && v1.IsInPosition(other.v0.position) && v0.IsInPosition(other.v1.position); } } public class CustomMesh { … private LinkedList<Edge> ObtainHullEdges(int[] triIndices) { var edges = new LinkedList<Edge>(); for (var i = 0; i < triIndices.Length; i++) { var edge = edges.Nodes().FirstOrDefault(e => e.Value.Coincides(Triangles[triIndices[i]].Edges[0])); if (edge != null) edges.Remove(edge); else edges.AddFirst(Triangles[triIndices[i]].Edges[0]); edge = edges.Nodes().FirstOrDefault(e => e.Value.Coincides(Triangles[triIndices[i]].Edges[1])); if (edge != null) edges.Remove(edge); else edges.AddFirst(Triangles[triIndices[i]].Edges[1]); edge = edges.Nodes().FirstOrDefault(e => e.Value.Coincides(Triangles[triIndices[i]].Edges[2])); if (edge != null) edges.Remove(edge); else edges.AddFirst(Triangles[triIndices[i]].Edges[2]); } return edges; } }
بعد تلقي جميع حواف الكفاف ، تحتاج إلى بناء الجدران المقابلة. هناك العديد من الخيارات للتنفيذ ، لكننا قررنا اتخاذ مسار أقل مقاومة - توليد متوازيات في اتجاه متجه الحركة على أساس الحواف بشكل منفصل. ونظرًا لأن لدينا جميعًا إزاحة واحدة ، نتيجة لهذا الإجراء ، ستشكل متوازي الأضلاع جدارًا صلبًا ومغلقًا لكل مجموعة. يبقى لتحديد اتجاه عناصر الجدار.
يتكون الجدار ، مثل الشبكة بالكامل ، من مثلثات.
وفقًا لاتفاقية OpenGL ، يتم تقديم مثلث منفصل على الشاشة إذا كان الالتفاف حولها عند عرض نقاطها على مستوى الشاشة يتوافق مع السير في اتجاه عقارب الساعة:
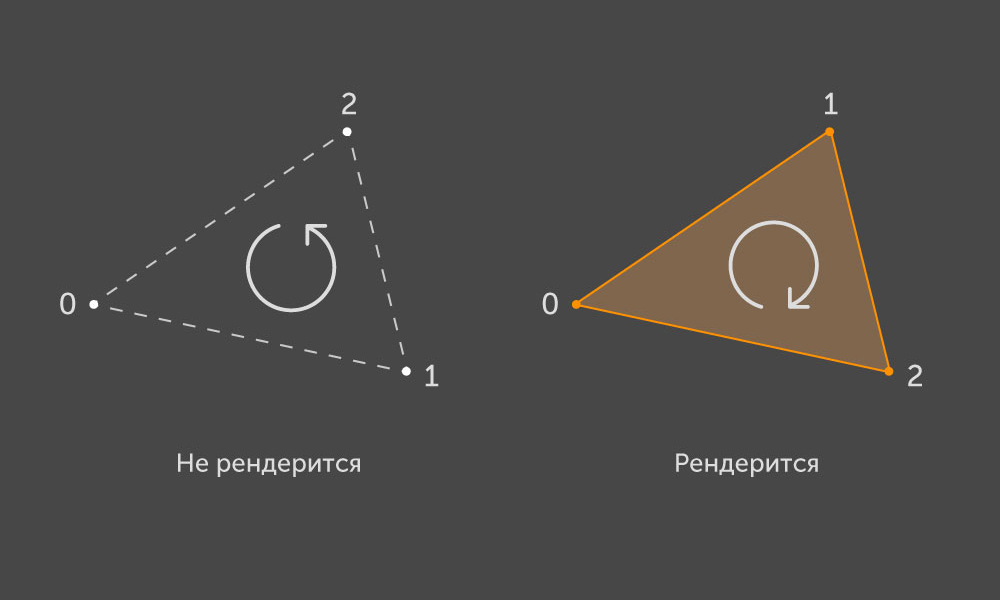
لذلك ، المثلث يتوافق مع ناقل معين معين يحدد الجانب الأمامي. يحد كل مثلث محيط محدب يتكون من ثلاثة حواف. كل حافة لها رأسان ممثلان في هيكلنا كـ
v0 و
v1 . نحدد اتجاه الحافة بحيث تكون
v0 هي البداية ،
v1 هي النهاية. الآن ، إذا تم تعيين اتجاه حواف المثلث وفقًا لتجاوز رؤوسه ، فيجب أن يكون لأي محيط خارجي للكتلة مسار جانبي إما في اتجاه عقارب الساعة أو عكس اتجاه عقارب الساعة ، وأي اتجاه داخلي بالعكس. قمنا بتطبيق وحدات إنشاء
CustomMesh و
Triangle بحيث يتوافق تقاطع رؤوس كل المثلثات مع اتجاه عقارب الساعة.
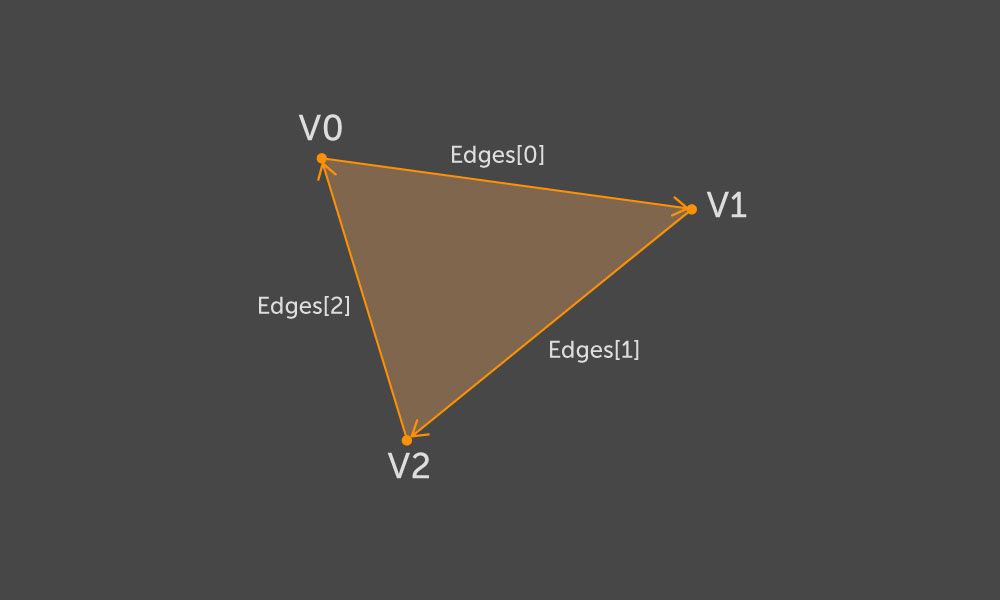
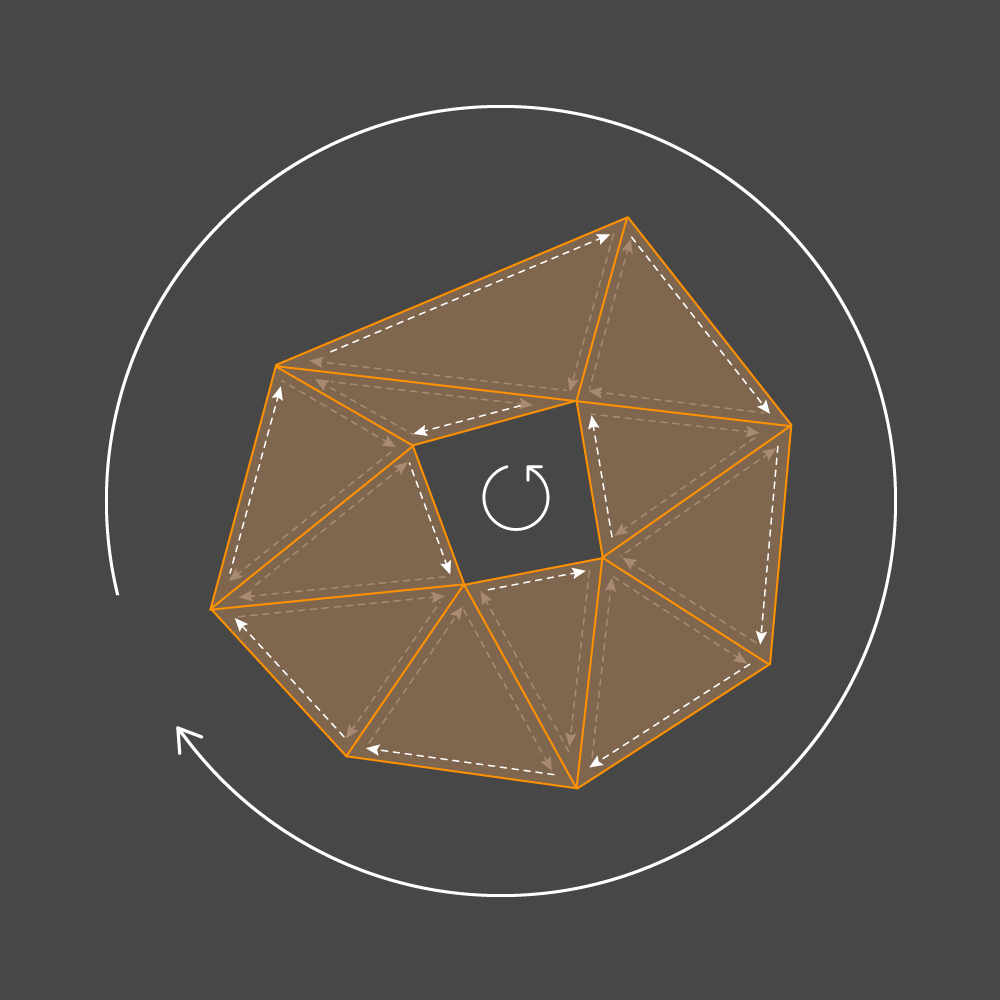
بوجود اتجاه للتحايل على المحيط ، يمكننا أن نقول على وجه اليقين أي جانب من الضلع هو الجزء الداخلي للكونتور ، والذي هو الجانب الخارجي. بناءً على هذه المعلومات ، سنختار اتجاه الجدار. دع (
v0 ، v1 ) هي الحافة التي يجب على أساسها إنشاء متوازي الاضلاع المرغوب فيه. نحن نأخذ النقطتين
v2 و
v3 كموضعي الإزاحة
v0 و
v1 . ثم نبني مثلثين وفقًا للمخطط التالي:
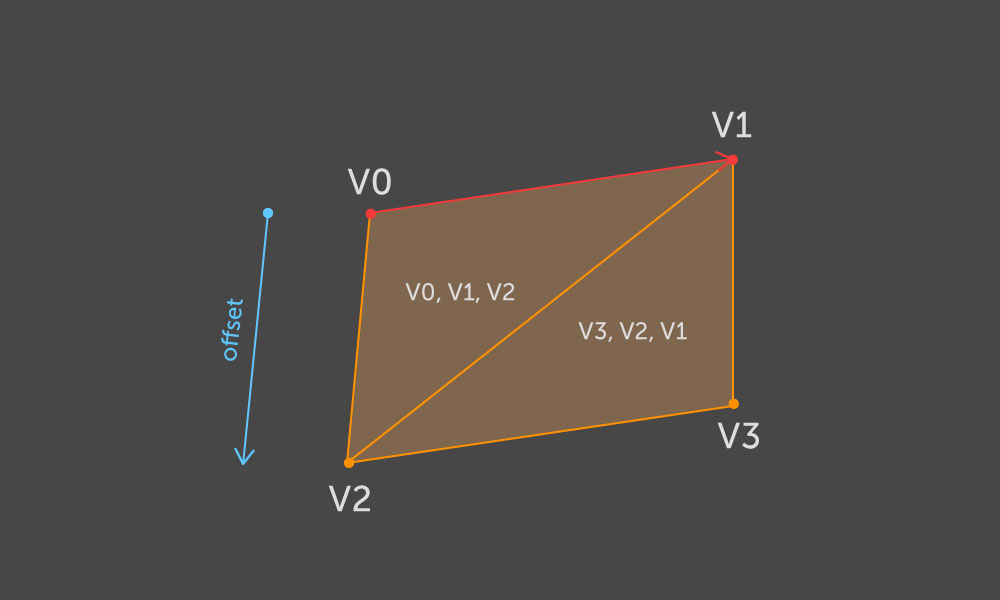
وهكذا لكل حافة كفاف.
سرد طريقة لبناء الجدران باستخدام قائمة الحواف public class CustomMesh { … private void ExtrudeEdgesSet(Edge[] edges, Vector3 offset) { if (offset == Vector3.zero || edges == null || edges.Length == 0) return; var initVerticesLength = vertices.Length; Array.Resize(ref vertices, initVerticesLength + edges.Length * 4); if (normals != null && normals.Length == initVerticesLength) { Array.Resize(ref normals, vertices.Length); } if (uv0 != null && uv0.Length == initVerticesLength) { Array.Resize(ref uv0, vertices.Length); } if (uv2 != null && uv2.Length == initVerticesLength) { Array.Resize(ref uv2, vertices.Length); } if (colors != null && colors.Length == initVerticesLength) { Array.Resize(ref colors, vertices.Length); } var initTrianglesLength = Triangles.Length; Array.Resize(ref Triangles, initTrianglesLength + edges.Length * 2); edges .AsParallel() .Select((edge, i) => { int j = initVerticesLength + i * 4; vertices[j] = edge.v0.position; vertices[j + 1] = edge.v1.position; vertices[j + 2] = edge.v0.position + offset; vertices[j + 3] = edge.v1.position + offset; if (normals != null && normals.Length == vertices.Length) { var normal = Vector3.Cross(vertices[j + 1] - vertices[j], offset); normals[j] = normals[j + 1] = normals[j + 2] = normals[j + 3] = normal; } if (uv0 != null && uv0.Length == vertices.Length) { uv0[j] = uv0[j + 2] = edge.v0.uv0; uv0[j + 1] = uv0[j + 3] = edge.v1.uv0; } if (uv2 != null && uv2.Length == vertices.Length) { uv2[j] = uv2[j + 2] = edge.v0.uv2; uv2[j + 1] = uv2[j + 3] = edge.v1.uv2; } if (colors != null && colors.Length == vertices.Length) { colors[j] = colors[j + 2] = edge.v0.color; colors[j + 1] = colors[j + 3] = edge.v1.color; } Triangles[initTrianglesLength + i * 2] = new Triangle( initTrianglesLength + i * 2, Id, j, j + 1, j + 2 ); Triangles[initTrianglesLength + i * 2 + 1] = new Triangle( initTrianglesLength + i * 2 + 1, Id, j + 3, j + 2, j + 1 ); return true; }).ToArray(); } }
مع هذا النهج ، سيكون الجانب الأمامي للجدران التي تم إنشاؤها صحيحًا للشرائح وللحفر. لا يوجد سوى قيد واحد مهم: مجموعة المثلثات التي يتم إجراء عملية
البثق بها لا ينبغي أن تكون ملفوفة حول نفسها فيما يتعلق بموجه الحركة.
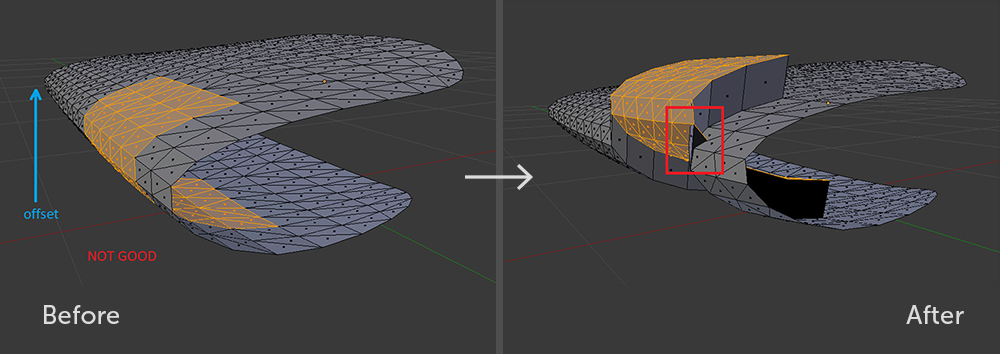 مجموعة فرعية من المضلعات غير صالحة فيما يتعلق بالإزاحة. حتى في Blender مع مثل Extrude ، لن يكون من الممكن تجنب منحنى الهندسة.
مجموعة فرعية من المضلعات غير صالحة فيما يتعلق بالإزاحة. حتى في Blender مع مثل Extrude ، لن يكون من الممكن تجنب منحنى الهندسة.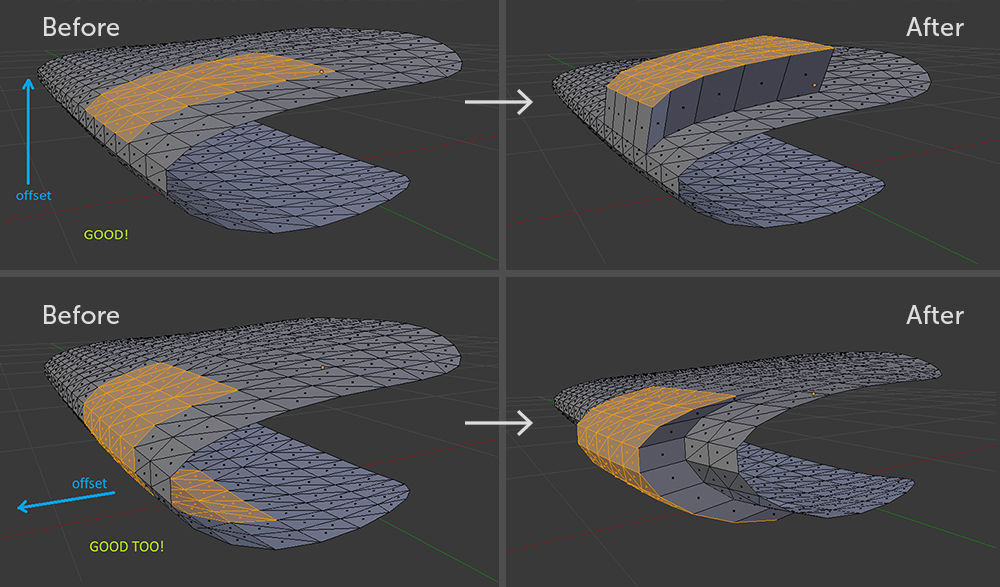 مجموعات فرعية صالحة من المضلعات
مجموعات فرعية صالحة من المضلعاتالجدار جاهز ، يبقى لتبديل المثلثات. من السهل فهم هذه الخطوة من الخوارزمية ، على الرغم من أن التطبيق تبين أنه مرهق.
في حالتنا ، نحن بحاجة إلى التأكد من أن كل قمة من الكتلة تنتمي فقط إلى مثلثاتها. إذا لم يتم استيفاء الشرط ، يمكن أن تصل بعض المضلعات المجاورة للمجموعة. يكمن الحل لهذا الموقف في تكرار كل قمة تنتمي إلى كل من الكتلة وبقية النموذج. بعد ذلك ، بالنسبة لجميع المضلعات في المجموعة ، استبدل مؤشر هذه القمة بفهرس مكرر. عندما يتم استيفاء الحالة ، ننقل جميع رؤوس المجموعة إلى ناقل الحركة.
سرد طريقة لتحويل مجموعة من المضلعات public class CustomMesh { … private void TranslateTrianglesHard(int[] triIndices, Vector3 offset, int[] hullVerts) { var newVertexIndices = new Dictionary<int, int>(); var initVerticesCount = vertices.Length; Triangles.Where((t, i) => !triIndices.Contains(i)).Select(t => { if (hullVerts.Contains(t.V0.Index) && !newVertexIndices.ContainsKey(t.V0.Index)) newVertexIndices.Add(t.V0.Index, initVerticesCount + newVertexIndices.Count); if (hullVerts.Contains(t.V1.Index) && !newVertexIndices.ContainsKey(t.V1.Index)) newVertexIndices.Add(t.V1.Index, initVerticesCount + newVertexIndices.Count); if (hullVerts.Contains(t.V2.Index) && !newVertexIndices.ContainsKey(t.V2.Index)) newVertexIndices.Add(t.V2.Index, initVerticesCount + newVertexIndices.Count); return false; }).ToArray(); Array.Resize(ref vertices, initVerticesCount + newVertexIndices.Count); foreach (var pair in newVertexIndices) vertices[pair.Value] = vertices[pair.Key] + offset; if (normals != null && normals.Length == initVerticesCount) { Array.Resize(ref normals, vertices.Length); foreach (var pair in newVertexIndices) normals[pair.Value] = normals[pair.Key]; } if (uv0 != null && uv0.Length == initVerticesCount) { Array.Resize(ref uv0, vertices.Length); foreach (var pair in newVertexIndices) uv0[pair.Value] = uv0[pair.Key]; } if (uv2 != null && uv2.Length == initVerticesCount) { Array.Resize(ref uv2, vertices.Length); foreach (var pair in newVertexIndices) uv2[pair.Value] = uv2[pair.Key]; } if (colors != null && colors.Length == initVerticesCount) { Array.Resize(ref colors, vertices.Length); foreach (var pair in newVertexIndices) colors[pair.Value] = colors[pair.Key]; } var alreadyMoved = new HashSet<int>(); for (var i = 0; i < triIndices.Length; i++) { if (newVertexIndices.ContainsKey(Triangles[triIndices[i]].V0.Index)) { var index = newVertexIndices[Triangles[triIndices[i]].V0.Index]; Triangles[triIndices[i]].Edges[0].v0.Index = index; Triangles[triIndices[i]].Edges[2].v1.Index = index; } else if (!alreadyMoved.Contains(Triangles[triIndices[i]].V0.Index)) { vertices[Triangles[triIndices[i]].V0.Index] += offset; alreadyMoved.Add(Triangles[triIndices[i]].V0.Index); } if (newVertexIndices.ContainsKey(Triangles[triIndices[i]].V1.Index)) { var index = newVertexIndices[Triangles[triIndices[i]].V1.Index]; Triangles[triIndices[i]].Edges[0].v1.Index = index; Triangles[triIndices[i]].Edges[1].v0.Index = index; } else if (!alreadyMoved.Contains(Triangles[triIndices[i]].V1.Index)) { vertices[Triangles[triIndices[i]].V1.Index] += offset; alreadyMoved.Add(Triangles[triIndices[i]].V1.Index); } if (newVertexIndices.ContainsKey(Triangles[triIndices[i]].V2.Index)) { var index = newVertexIndices[Triangles[triIndices[i]].V2.Index]; Triangles[triIndices[i]].Edges[1].v1.Index = index; Triangles[triIndices[i]].Edges[2].v0.Index = index; } else if (!alreadyMoved.Contains(Triangles[triIndices[i]].V2.Index)) { vertices[Triangles[triIndices[i]].V2.Index] += offset; alreadyMoved.Add(Triangles[triIndices[i]].V2.Index); } } } }
القيام به. الآن ، بإضافة نتائج جميع الخطوات ، نحصل على ثقب أو تل.
سرد الطريقة النهائية لعملية Extrude public class CustomMesh { … public void ExtrudeTriangles(int[] triIndices, Vector3 offset) { var edges = ObtainHullEdges(triIndices); ExtrudeEdgesSet(edges.ToArray(), offset); var hullVertices = edges.Select(edge => edge.v0.Index).ToArray(); TranslateTrianglesHard(triIndices, offset, hullVertices); } }
بعد أن لعبت مع إحداثيات فحص النسيج وإزاحة نقاط الكنتور ، يمكنك الحصول على فترة راحة:

وهذا ليس كل شيء
بالإضافة إلى عمليات التحرير التي تمت مناقشتها أعلاه ، نستخدم أيضًا طرقًا ملائمة أخرى للتعامل مع النماذج.
على سبيل المثال ، لقد كتبنا بالإضافة إلى ذلك أسلوب
Combine () لدمج اثنين
CustomMesh . الفرق الرئيسي بين تطبيقنا و
UnityEngine.Mesh.CombineMeshes () هو أنه إذا كانت بعض الرؤوس متساوية تمامًا عند الجمع بين الشبكات ، فإننا نترك واحدًا منها فقط ، وبالتالي نتجنب الهندسة غير الضرورية.
في نفس الوحدة ، قمنا بتنفيذ
خوارزمية تثليث طائرة Delaunay . باستخدامه ، يمكنك ، على سبيل المثال ، إغلاق ثقب كبير تم إنشاؤه باستخدام
Extrude بغطاء مسطح بنسيج مائي والحصول على بحيرة:

حسنًا ، صنفها! في المقالة التالية ، سننظر في ميزات استيراد
.fbx في
الوحدة وأساليب التحقق من النموذج في المشروع.
لتناول وجبة خفيفة (فقط للولز)