كيف يتحول الخطأ إلى الخطيئة

تقول إحدى الأساطير الحضرية إن خالق أكياس السكر ، العصي ، شنق نفسه عندما علم أن المستهلكين لا يكسرونها إلى النصف على فنجان واحد ، لكنهم يمزقون الطرف بلطف. هذا بالطبع ليس كذلك ، ولكن إذا تم اتباع هذا المنطق ، فلا ينبغي لأحد محبي بيرة غينيس البريطانية باسم ويليام جوسيت أن يعلق نفسه فقط ، ولكن بالتناوب في التابوت يجب أن يحفر الأرض بالفعل في المنتصف. وكل ذلك بسبب اختراعه الأيقوني ، المنشور تحت اسم الطالب المستعار ، وقد أسيء استخدامه بشكل كارثي منذ عقود.

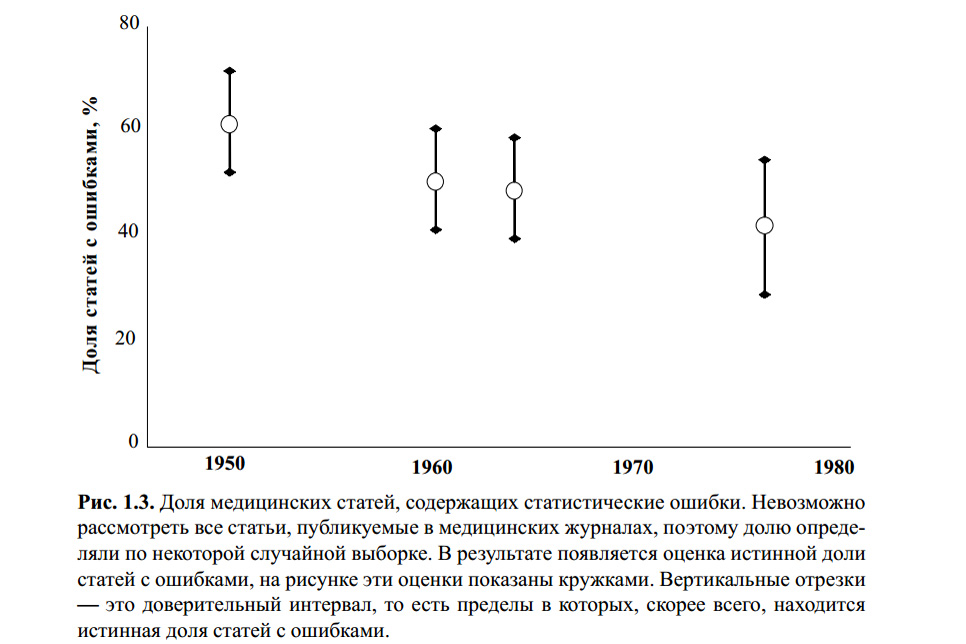
الشكل أعلاه هو من كتاب S. Glanz. الإحصاءات الطبية الحيوية. لكل من الانجليزية - M.، Practice، 1998 .-- 459 p. لا أعرف ما إذا كان أي شخص قام بالتحقق من الأخطاء الإحصائية لحسابات هذا المخطط. ومع ذلك ، يشير عدد من المقالات الحديثة حول الموضوع ، وتجربتي الخاصة إلى أن معيار الطالب t لا يزال الأكثر شهرة ، وبالتالي الأكثر شعبية في الاستخدام ، مع أو بدون.

والسبب في ذلك هو التعليم السطحي (يعلم المعلمون الصارمون أنك بحاجة إلى "التحقق من الإحصاءات" ، وإلا uuuuuu!) ، وسهولة الاستخدام (تتوفر الجداول والآلات الحاسبة عبر الإنترنت بالكثير) وممانعة عادية في الخوض في حقيقة أن "وهكذا يعمل". سيقول معظم الأشخاص الذين استخدموا هذا المعيار مرة واحدة على الأقل في مسارهم أو حتى في العمل العلمي شيئًا مثل: "حسنًا ، لقد قارنا 5 تلاميذ غاضبين و 7 من تلاميذ المدارس من حيث العدوان ، قيمة جدولنا تقترب من p = 0.05 وهذا يعني أن الألعاب شريرة. حسنًا ، نعم ، ليس بالضبط ، ولكن مع احتمال 95 ٪. " كم عدد الأخطاء المنطقية والمنهجية التي ارتكبوها؟

الأساسيات

ما هو اختبار الطالب على أساس؟ المنطق مأخوذ من النظرية البايزية ، الأساس الرياضي هو من التوزيع الغوسي ، وتستند المنهجية على تحليل التباين:

حيث المعلمة μ هي التوقع الرياضي (القيمة المتوسطة) للتوزيع ، والمعلمة σ هي الانحراف المعياري (σ ² هو التباين) للتوزيع.

ما هو تحليل التباين؟ تخيل جمهور هبر ، مرتبة حسب عدد الأشخاص في كل عصر. من المحتمل أن يطيع عدد الأشخاص حسب العمر التوزيع الطبيعي - وفقًا لوظيفة Gauss:

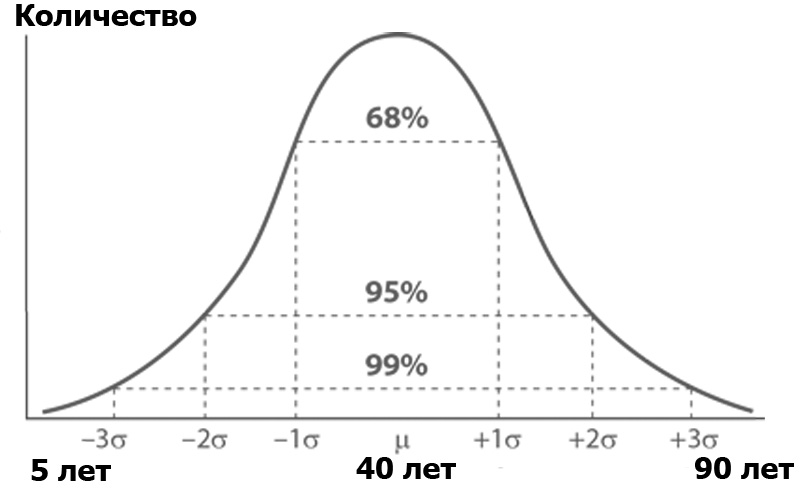
يحتوي التوزيع العادي على خاصية مثيرة للاهتمام - كل قيمها تقريبًا تكمن في حد الانحرافات المعيارية الثلاثة عن متوسط ​​القيمة. وما هو الانحراف المعياري؟ هذا هو أصل التباين. التشتت ، بدوره ، هو مجموع مربعات الفرق بين جميع أفراد المجتمع ومتوسط ​​القيمة مقسومًا على عدد هؤلاء الأعضاء:

$$

$$σ_ {n} ^ {2} = {\ frac {1} {n}} \ sum \ limit _ {{i = 1}} ^ {n} \ left (X_ {i} - {\ bar {X} } \ right) ^ {2}$$

وهذا يعني أن كل قيمة تم طرحها من المتوسط ​​، وتربيعها لقتل السلبيات ، ثم أخذت المتوسط ​​، تلخيصها بغباء ومقسمة على عدد هذه القيم. والنتيجة هي مقياس لمتوسط ​​تشتت القيم بالنسبة لمتوسط ​​التباين.

تخيل أننا اخترنا عينتين في هذه الفئة العامة من السكان : قارئات لوحة Cryptocurrency وقارئات Old Iron. من خلال عمل عينة عشوائية ، نحصل دائمًا على توزيعات قريبة من وضعها الطبيعي . والآن لدينا موزع صغير داخل سكاننا:

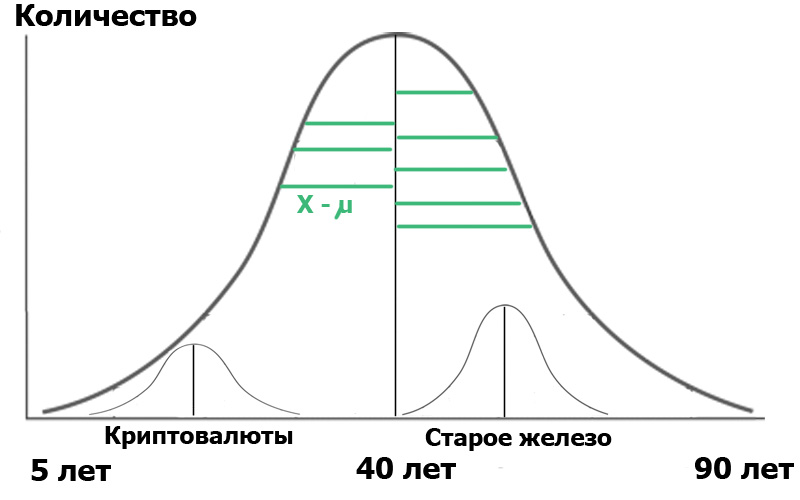
من أجل الوضوح ، عرضت شرائح خضراء - المسافة من نقاط التوزيع إلى متوسط ​​القيمة. إذا كانت أطوال هذه الشرائح الخضراء مربعة وملخصة ومتوسطها - فسيكون هذا هو الفرق.

والآن - الاهتمام. يمكننا توصيف السكان من خلال هاتين العينات الصغيرة. من ناحية ، تميز تباينات العينات تباين السكان بأكملهم. من ناحية أخرى ، فإن متوسط ​​قيم العينات نفسها هو أيضًا أرقام يمكن حساب التباين! لذلك: لدينا متوسط ​​تباينات العينات والتباين في متوسط ​​قيم العينات.

ثم يمكننا إجراء تحليل التباين ، وتمثيله تقريبًا في شكل معادلة منطقية:

$$

$$F = {\ frac {variance \: السكان \: حسب \: المتوسط ​​\: القيم \: العينات} {variance \: السكان \: بواسطة \: الفروق \: العينات}}$$

ما سوف تعطينا الصيغة أعلاه؟ بسيط جدا في الإحصائيات ، يبدأ كل شيء بـ "الفرضية الفارغة" ، والتي يمكن صياغتها على أنها "بدت لنا" ، "كل الصدف عشوائية" - بمعنى ، و "لا توجد صلة بين الحدثين المرصدين" - إذا كان بدقة. لذلك ، في حالتنا ، فإن الفرضية الفارغة هي عدم وجود فروق ذات دلالة إحصائية بين التوزيع العمري لمستخدمينا في محورين. في حالة الفرضية الفارغة ، سيبدو الرسم التخطيطي لدينا مثل هذا:

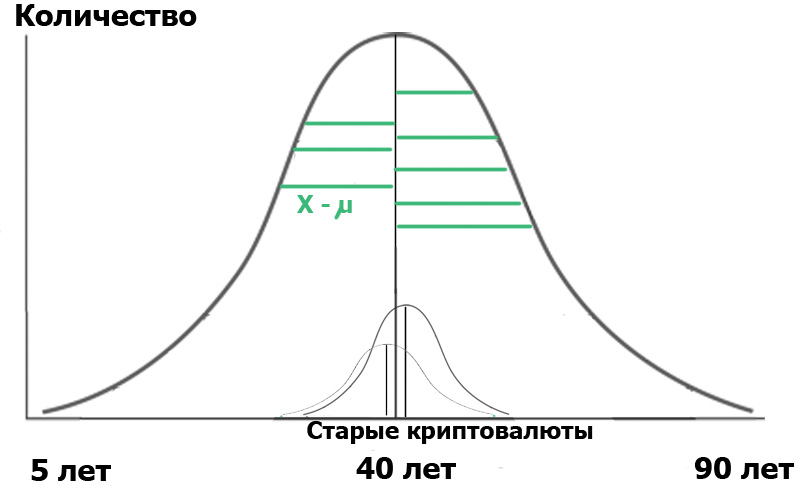
هذا يعني أن كل من تباينات العينات وقيمها المتوسطة قريبة جدًا أو مساوية لبعضها البعض ، وبالتالي ، بشكل عام ، معيارنا

$$

$$F = {\ frac {variance \: السكان \: حسب \: المتوسط ​​\: القيم \: العينات} {variance \: السكان \: حسب \: الفروق \: العينات}} = 1$$

لكن إذا كانت تباينات العينات متساوية ، لكن أعمار الناجحين مختلفة حقًا ، فسيكون البسط (تباين القيم المتوسطة) كبيرًا ، وستكون F أكبر بكثير من الوحدة. ثم سيبدو الشكل أكثر في الشكل السابق. وماذا سوف يعطينا؟ لا شيء ، إذا كنت لا تولي اهتماما للصياغة: ستكون الفرضية الفارغة هي عدم وجود اختلافات كبيرة .

لكن الأهمية ... وضعناها بأنفسنا. يشار إلى أنه α وله المعنى التالي: مستوى الأهمية هو أقصى احتمال مقبول لرفض الفرضية الخاطئة عن طريق الخطأ . بمعنى آخر ، سننظر إلى حدثنا على أنه فرق كبير بين مجموعة وأخرى ، فقط إذا كان الاحتمال P لخطأنا أقل من α. هذا هو p <0.05 سيئ السمعة ، لأنه عادة في البحوث الطبية الحيوية يتم تحديد مستوى الأهمية عند 5٪.

حسنًا ، كل شيء بسيط. اعتمادًا على α ، هناك قيم حرجة لـ F ، نبدأ من خلالها برفض الفرضية الصفرية. يتم إصدارها في شكل جداول ، ونحن معتادون على استخدامها. هذا هو لتحليل التباين. وماذا عن الطالب؟

هكذا قال الطالب

ومعيار الطالب هو مجرد حالة خاصة لتحليل التباين. مرة أخرى ، لن أفرط في عبئك على الصيغ التي يسهل الوصول إليها عبر google ، لكنني سأنقل الجوهر:

$$

$$t = {\ frac {الفرق \: يعني \: القيم \: العينات} {قياسي \: خطأ \: الاختلافات \: sample \: mean}}$$

لذلك ، كان كل هذا التفسير الطويل بحاجة إلى أن يكون وقحًا للغاية ويتحدث بطلاقة ، ولكنه يوضح بوضوح ما يستند إليه المعيار t. وبناءً على ذلك ، من خلال خصائصه الكامنة ، اتبع مباشرة قيود استخدامه ، والتي يخطئ العلماء المحترفون في كثير من الأحيان في ارتكابها لأخطاء.

الخاصية الأولى: طبيعية التوزيع.

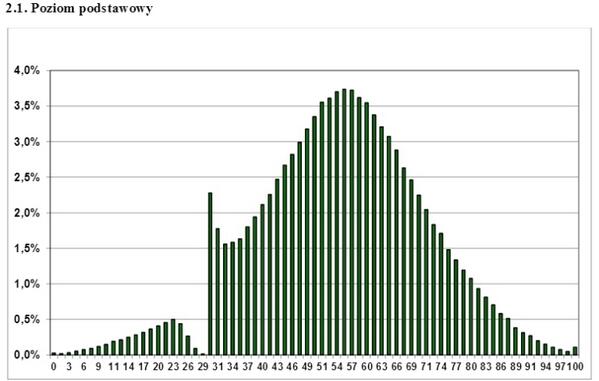
هذا هو بضع سنوات كرسم بياني لتوزيع علامات امتحان الدولة البولندية على شبكة الإنترنت. ما الاستنتاج الذي يمكن استخلاصه منه؟ أن هذا الامتحان لا يمر فقط صدت بالكامل جوبنيك؟ ما المعلمين "الوصول" الطلاب؟ لا ، واحد فقط - لتوزيع غير الطبيعي ، لا يمكنك تطبيق معايير التحليل حدودي ، مثل الطالب. إذا كان لديك مخطط توزيع أحادي الجانب ، مسنن ، متموج ، منفصل - نسيان المعيار t ، لا يمكنك استخدامه. ومع ذلك ، في بعض الأحيان يتم تجاهل هذا بنجاح حتى من خلال العمل العلمي الجاد.

ماذا تفعل في هذه الحالة؟ استخدام ما يسمى معايير التحليل اللامعلمية. إنهم يطبقون طريقة مختلفة ، وهي تصنيف البيانات ، أي الابتعاد عن قيم كل نقطة من النقاط إلى الترتيب المخصص لها. هذه المعايير أقل دقة من تلك المعايير ، ولكن على الأقل استخدامها صحيح ، على عكس الاستخدام غير المبرر للمعيار المحدد على مجموعة غير طبيعية. من بين هذه المعايير ، يُعرف معيار مان ويتني U ، وغالبًا ما يتم استخدامه كمعيار "لعينة صغيرة". نعم ، يتيح لك التعامل مع عينات تصل إلى 5 نقاط ، ولكن هذا ، كما ينبغي أن يكون واضحًا بالفعل ، ليس هو الغرض الرئيسي منه.

الخاصية الثانية: هل تتذكر الصيغة؟ تغيرت قيم المعيار F مع اختلاف (التباين المتزايد) لمتوسط ​​قيم العينات . لكن القاسم ، أي الاختلافات نفسها ، يجب ألا يتغير. لذلك ، ينبغي أن يكون معيار الفروق هو معيار آخر للتطبيق. يقال حقيقة أن هذا الفحص أقل في كثير من الأحيان ، على سبيل المثال ، هنا: أخطاء في التحليل الإحصائي للبيانات الطبية الحيوية. ليونوف ف. المجلة الدولية للممارسة الطبية ، 2007 ، لا. 2 ، ص 19-35 .

الخاصية الثالثة: مقارنة عينتين. يحبون استخدام المعيار t لمقارنة أكثر من مجموعتين. يتم ذلك عادة على النحو التالي: تتم مقارنة الفروق بين المجموعة A من B ، B من C ، و A من C. في أزواج ، ثم بناءً على ذلك ، يتم استنتاج معين ، وهذا غير صحيح تمامًا. في هذه الحالة ، ينشأ تأثير المقارنات المتعددة.
بعد الحصول على قيمة عالية بما فيه الكفاية لـ t في أي من المقارنات الثلاثة ، أبلغ الباحثون أن "P <0.05". لكن في الواقع ، يزيد احتمال الخطأ بشكل كبير عن 5٪.

لماذا؟

لقد اكتشفنا ذلك: على سبيل المثال ، اعتمدت الدراسة مستوى دلالة 5 ٪. هذا يعني أن الحد الأقصى المقبول للفرص الخاطئة للرفض الخاطئ عند مقارنة المجموعتين A و B هو 5٪. يبدو أن كل شيء صحيح؟ ولكن سيحدث الخطأ نفسه بالضبط في حالة مقارنة المجموعتين B و C ، وعند مقارنة المجموعتين A و C أيضًا. وبالتالي ، فإن احتمال ارتكاب خطأ ككل مع هذا النوع من التقييم لن يكون 5 ٪ ، ولكن أكثر من ذلك بكثير. بشكل عام ، هذا الاحتمال يساوي
P ′ = 1 - (1 - 0.05) ^ ك
حيث k هو عدد المقارنات.

ثم ، في دراستنا ، فإن احتمال ارتكاب خطأ في رفض فرضية فارغة هو ما يقرب من 15 ٪. عند مقارنة المجموعات الأربع ، يكون عدد الأزواج ، وبالتالي ، المقارنات الزوجية المحتملة هو 6. وبالتالي ، مع وجود مستوى دلالة في كل من المقارنات 0.05
احتمال اكتشاف خطأ عن طريق الخطأ في واحد على الأقل لم يعد 0.05 ، ولكن 0.31.

لا يزال ، هذا الخطأ ليس من الصعب القضاء عليها. طريقة واحدة هي تقديم تعديل Bonferroni. يخبرنا عدم المساواة في Bonferroni أنه إذا قمت بتطبيق المعايير k الأوقات
مع مستوى دلالة α ، ثم الاحتمال ، في حالة واحدة على الأقل ، لإيجاد فرق حيث لا وجود له لا يتجاوز ناتج k بواسطة α. من هنا:
α ′ <αk ،
حيث α ′ هو احتمالية الخلط بين الاختلافات مرة واحدة على الأقل. ثم يتم حل مشكلتنا بكل بساطة: نحتاج إلى تقسيم مستوى أهميتنا على تصحيح Bonferroni - أي بتعدد المقارنات. لثلاثة مقارنات ، نحتاج إلى أخذ القيم المقابلة لـ α = 0.05 / 3 = 0.0167 من جداول اختبار t. أكرر - إنه بسيط للغاية ، لكن هذا التعديل لا يمكن تجاهله. بالمناسبة ، يجب ألا تتأثر بهذا التعديل ، حتى بعد القسمة على 8 ، فإن قيم المعيار t أكثر صرامة بشكل غير ضروري.

بعد ذلك ، تأتي "الأشياء الصغيرة" التي لا يلاحظونها على الإطلاق. أنا لا أقدم بصيغ هنا عمداً ، حتى لا تقلل من قابلية قراءة النص ، ولكن يجب أن نتذكر أن حسابات المعيار t تختلف في الحالات التالية:

• أحجام مختلفة من عينتين (بشكل عام ، تذكر أنه في الحالة العامة نقارن مجموعتين باستخدام صيغة معيار العينة) ؛

  
  

• توافر العينات التابعة. هذه هي الحالات التي يتم فيها قياس البيانات من مريض واحد على فترات زمنية مختلفة ، وبيانات من مجموعة من الحيوانات قبل وبعد التجربة ، إلخ.

  
  

أخيرًا ، حتى تتمكن من تخيل المدى الكامل لما يحدث ، سأقدم بيانات أكثر حداثة حول الاستخدام غير الصحيح لمعيار t. الأرقام في عامي 1998 و 2008 لعدد من المجلات العلمية الصينية ، ويتحدثون عن أنفسهم. أريد حقًا أن يتحول هذا إلى إهمال في التصميم أكثر من البيانات العلمية غير الدقيقة:

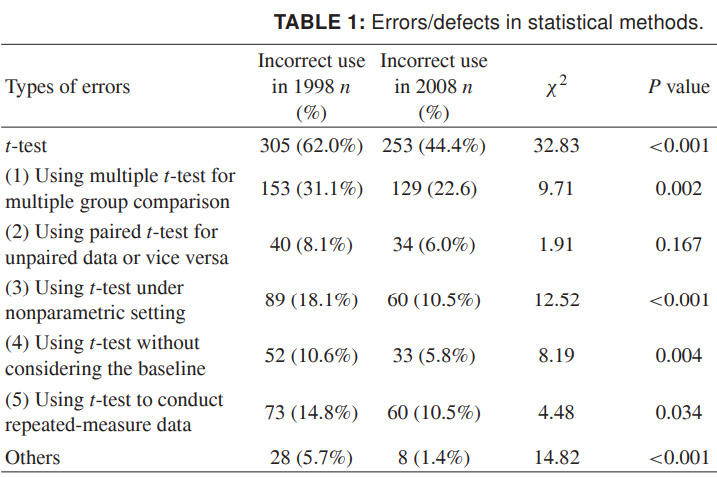
المصدر: إساءة استخدام الأساليب الإحصائية في 10 من المجلات الطبية الصينية الرائدة في عامي 1998 و 2008. Shunquan Wu et al ، المجلة العلمية العالمية ، 2011 ، 11 ، 2106-2114

تذكر أن الأهمية المنخفضة للنتائج ليست بالأمر المحزن كنتيجة خاطئة. من المستحيل الوصول إلى الخطيئة العلمية - استنتاجات كاذبة - عن طريق تشويه البيانات بإحصائيات مطبقة بشكل غير صحيح.

حول التفسير المنطقي ، بما في ذلك البيانات الإحصائية غير الصحيحة ، ربما أخبرني بشكل منفصل.

اقرأها بشكل صحيح.