سيارة الجبل: حل التحدي الكلاسيكي مع التدريب التعزيز

وكقاعدة عامة ، تعتبر التعديلات على الخوارزميات التي تعتمد على الميزات المحددة لمهمة معينة أقل قيمة ، حيث يصعب تعميمها على فئة أوسع من المشاكل. ومع ذلك ، هذا لا يعني أن مثل هذه التعديلات ليست ضرورية. علاوة على ذلك ، في كثير من الأحيان يمكنهم تحسين النتيجة بشكل كبير حتى بالنسبة للمشاكل الكلاسيكية البسيطة ، وهو أمر مهم للغاية في التطبيق العملي للخوارزميات. على سبيل المثال ، في هذا المنشور ، سأحل مشكلة Mountain Car من خلال التدريب على التعزيز وأظهر أنه باستخدام معرفة كيفية تنظيم المهمة ، يمكن حلها بشكل أسرع.

عن نفسي

اسمي Oleg Svidchenko ، والآن أنا أدرس في كلية العلوم الفيزيائية والرياضية وعلوم الكمبيوتر في سان بطرسبرج HSE ، قبل أن أدرس في جامعة سان بطرسبرج لمدة ثلاث سنوات. أنا أعمل أيضًا في JetBrains Research كباحث. قبل دخولي إلى الجامعة ، درست في SSC بجامعة موسكو الحكومية وأصبحت الفائز في أولمبياد عموم روسيا لتلاميذ علوم الكمبيوتر كجزء من فريق موسكو.

ماذا نحتاج؟

إذا كنت مهتمًا بتجربة التدريب على التعزيز ، فإن تحدي Mountain Car يعد أمرًا رائعًا لهذا الغرض. نحتاج اليوم إلى Python مع مكتبات Gym و PyTorch المثبتة ، بالإضافة إلى المعرفة الأساسية بالشبكات العصبية.

وصف المهمة

في عالم ثنائي الأبعاد ، تحتاج السيارة إلى الصعود من الجوف بين تلة إلى أعلى التل الأيمن. إنه أمر معقد بسبب حقيقة أنها لا تملك قوة محرك كافية للتغلب على قوة الجاذبية والدخول إلى هناك في المحاولة الأولى. نحن مدعوون لتدريب وكيل (في حالتنا ، شبكة عصبية) يمكنه ، من خلال التحكم فيه ، تسلق التل الأيمن في أسرع وقت ممكن.

يتم التحكم في الماكينة من خلال التفاعل مع البيئة. وهي مقسمة إلى حلقات مستقلة ، ويتم تنفيذ كل حلقة خطوة بخطوة. في كل خطوة ، يستقبل الوكيل الحالة والبيئة من البيئة استجابة للإجراء بالإضافة إلى ذلك ، في بعض الأحيان قد يبلغ الوسيط بالإضافة إلى ذلك أن الحلقة قد انتهت. في هذه المشكلة ، s هو زوج من الأرقام ، أولهما هو موضع السيارة على المنحنى (إحداثي واحد يكفي ، لأننا لا نستطيع تمزيق أنفسنا عن السطح) ، والثاني هو سرعته على السطح (مع وجود إشارة). المكافأة r هي رقم يساوي دائمًا -1 لهذه المهمة. بهذه الطريقة ، نشجع الوكيل على إكمال الحلقة في أسرع وقت ممكن. لا يوجد سوى ثلاثة إجراءات ممكنة: دفع السيارة إلى اليسار ، لا تفعل شيئًا وادفع السيارة إلى اليمين. تتوافق هذه الإجراءات مع الأرقام من 0 إلى 2. قد تنتهي الحلقة إذا وصلت السيارة إلى أعلى التل الأيمن أو إذا اتخذ الوكيل 200 خطوة.

قليلا من الناحية النظرية

على هابري ، كان هناك بالفعل مقال عن DQN وصف فيه المؤلف جيدًا جميع النظريات اللازمة. ومع ذلك ، لسهولة القراءة ، سأكررها هنا بشكل أكثر رسمية.

يتم تعريف مهمة التعلم التعزيز من خلال مجموعة من مساحة الدولة S ، مساحة العمل A ، معامل $$$\ gamma$، ووظائف الانتقال T ووظائف المكافأة R. في الحالة العامة ، يمكن أن تكون وظيفة النقل ووظيفة المكافآت متغيرات عشوائية ، ولكن الآن سننظر في إصدار أكثر بساطة يتم تعريفهما بهما بشكل فريد. الهدف هو تعظيم المكافآت التراكمية. $$$\ sum_ {t = 0} ^ {T} r_ {t} \ cdot \ gamma ^ {t}$، حيث t هو رقم الخطوة في الوسط ، و T هو عدد الخطوات في الحلقة.

لحل هذه المشكلة ، نعرّف قيمة الدالة V للحالة بأنها قيمة المكافأة التراكمية القصوى ، شريطة أن نبدأ في الحالة. من خلال معرفة هذه الوظيفة ، يمكننا حل المشكلة ببساطة عن طريق تمرير كل خطوة إلى s بأقصى قيمة ممكنة. ومع ذلك ، ليس كل شيء بهذه البساطة: في معظم الحالات ، لا نعرف الإجراء الذي سينقلنا إلى الحالة المطلوبة. لذلك ، نضيف الإجراء كمعلمة ثانية للدالة. تسمى الوظيفة الناتجة دالة Q. يُظهر الحد الأقصى للمكافأة التراكمية الممكنة التي يمكن أن نحصل عليها من خلال تنفيذ إجراء في الحالة. ولكن يمكننا بالفعل استخدام هذه الوظيفة لحل المشكلة: في الحالة ، نختار ببساطة أن تكون Q (s، a) هي الحد الأقصى.

في الممارسة العملية ، لا نعرف وظيفة Q الحقيقية ، ولكن يمكننا تقريبها بطرق مختلفة. إحدى هذه التقنيات هي شبكة Deep Q Network (DQN). فكرته هي أنه بالنسبة لكل إجراء من الإجراءات ، فإننا نقدر تقريبًا وظيفة Q - باستخدام شبكة عصبية.

البيئة

الآن دعنا نذهب إلى الممارسة. أولاً ، نحن بحاجة إلى معرفة كيفية محاكاة بيئة MountainCar. ستساعدنا مكتبة Gym ، التي توفر عددًا كبيرًا من بيئات التعلم المعززة القياسية ، في التعامل مع هذه المهمة. لإنشاء بيئة ، نحتاج إلى استدعاء الأسلوب make على وحدة الصالة الرياضية لتمريرها اسم البيئة المطلوبة كمعلمة:

import gym env = gym.make("MountainCar-v0") 

يمكن العثور على الوثائق المفصلة هنا ، ويمكن العثور على وصف للبيئة هنا .
دعونا نفكر بمزيد من التفصيل في ما يمكننا القيام به بالبيئة التي أنشأناها:

• env.reset() - ينهي الحلقة الحالية ويبدأ حلقة جديدة. إرجاع الحالة الأولية.
• env.step(action) - ينفذ الإجراء المحدد. إرجاع حالة جديدة ومكافأة وما إذا كانت الحلقة قد انتهت ومعلومات إضافية يمكن استخدامها لتصحيح الأخطاء.
• env.seed(seed) - يضع بذرة عشوائية. يعتمد ذلك على كيفية إنشاء الحالات الأولية أثناء env.reset ().
• env.render() - يعرض الحالة الحالية للبيئة.

نحن ندرك DQN

DQN هي خوارزمية تستخدم شبكة عصبية لتقييم دالة Q. في المقال الأصلي ، حدد DeepMind البنية القياسية لألعاب أتاري باستخدام الشبكات العصبية التلافيفية. على عكس هذه الألعاب ، لا تستخدم Mountain Car الصورة كدولة ، لذلك سيتعين علينا تحديد العمارة بأنفسنا.

خذ على سبيل المثال بنية بها طبقتان مخفيتان من 32 خلية في كل منهما. بعد كل طبقة مخفية ، سوف نستخدم ReLU كدالة تنشيط. يتم تغذية رقمين يصفان الحالة لمدخلات الشبكة العصبية ، وفي الناتج نحصل على تقدير لوظيفة Q.

 import torch.nn as nn model = nn.Sequential( nn.Linear(2, 32), nn.ReLU(), nn.Linear(32, 32), nn.ReLU(), nn.Linear(32, 3) ) target_model = copy.deepcopy(model) #    def init_weights(layer): if type(layer) == nn.Linear: nn.init.xavier_normal(layer.weight) model.apply(init_weights) 

نظرًا لأننا سنقوم بتدريب الشبكة العصبية على وحدة معالجة الرسومات ، نحتاج إلى تحميل شبكتنا هناك:

 #     CPU,  “cuda”    “cpu” device = torch.device("cuda") model.to(device) target_model.to(device) 

سيكون متغير الجهاز عالميًا ، حيث سنحتاج أيضًا إلى تحميل البيانات.

نحتاج أيضًا إلى تحديد مُحسِّن يقوم بتحديث أوزان النموذج باستخدام النسب المتدرج. نعم ، هناك أكثر من واحد.

 optimizer = optim.Adam(model.parameters(), lr=0.00003) 

الآن نعلن عن وظيفة ستنظر في وظيفة الخطأ ، التدرج اللوني على طولها ، وتطبيق النسب. ولكن قبل ذلك تحتاج إلى تنزيل البيانات من الدُفعة إلى وحدة معالجة الرسومات:

 state, action, reward, next_state, done = batch #       state = torch.tensor(state).to(device).float() next_state = torch.tensor(next_state).to(device).float() reward = torch.tensor(reward).to(device).float() action = torch.tensor(action).to(device) done = torch.tensor(done).to(device) 

بعد ذلك ، نحتاج إلى حساب القيم الحقيقية لوظيفة Q- ، ولكن بما أننا لا نعرفها ، فسنقوم بتقييمها من خلال قيم الحالة التالية:

 target_q = torch.zeros(reward.size()[0]).float().to(device) with torch.no_grad(): #     Q-function    target_q = target_model(next_state).max(1)[0].view(-1) target_q[done] = 0 target_q = reward + target_q * gamma 

والتنبؤ الحالي:

 q = model(state).gather(1, action.unsqueeze(1)) 

باستخدام target_q و q ، نقوم بحساب دالة الخسارة وتحديث النموذج:

 loss = F.smooth_l1_loss(q, target_q.unsqueeze(1)) #      optimizer.zero_grad() #     loss.backward() #   . ,       for param in model.parameters(): param.grad.data.clamp_(-1, 1) #    optimizer.step() 

نظرًا لأن النموذج يأخذ في الاعتبار وظيفة Q- فقط ، ولا يقوم بأي إجراءات ، فنحن بحاجة إلى تحديد الوظيفة التي ستقرر الإجراءات التي سيقوم الوكيل بتنفيذها. كخوارزمية صنع القرار ، نأخذ $$$\ varepsilon$السياسة الجشع. فكرتها هي أن الوكيل عادة ما يقوم بأفعال جشعة ، ويختار الحد الأقصى لوظيفة Q ، ولكن مع احتمال $$$\ varepsilon$سوف يتخذ إجراء عشوائي. هناك حاجة إلى إجراءات عشوائية حتى تتمكن الخوارزمية من فحص تلك الإجراءات التي لن يتم تنفيذها وفقًا لسياسة الجشع فقط - وتسمى هذه العملية الاستكشاف.

 def select_action(state, epsilon, model): if random.random() < epsilon: return random.randint(0, 2) return model(torch.tensor(state).to(device).float().unsqueeze(0))[0].max(0)[1].view(1, 1).item() 

بما أننا نستخدم الدُفعات لتدريب الشبكة العصبية ، فنحن بحاجة إلى مخزن مؤقت سنخزن فيه تجربة التفاعل مع البيئة ومن أين سنختار الدُفعات:

 class Memory: def __init__(self, capacity): self.capacity = capacity self.memory = [] self.position = 0 def push(self, element): """    """ if len(self.memory) < self.capacity: self.memory.append(None) self.memory[self.position] = element self.position = (self.position + 1) % self.capacity def sample(self, batch_size): """    """ return list(zip(*random.sample(self.memory, batch_size))) def __len__(self): return len(self.memory) 

قرار ساذج

أولاً ، أعلن الثوابت التي سنستخدمها في عملية التعلم ، وقم بإنشاء نموذج:

 #  model   target model target_update = 1000 #  ,      batch_size = 128 #   max_steps = 100001 #  exploration max_epsilon = 0.5 min_epsilon = 0.1 #    memory = Memory(5000) model, target_model, optimizer = create_new_model() 

على الرغم من حقيقة أنه سيكون من المنطقي تقسيم عملية التفاعل إلى حلقات ، لوصف عملية التعلم ، فمن الأنسب أن نقسمها إلى خطوات منفصلة ، لأننا نريد أن نجعل خطوة واحدة من نزول التدرج بعد كل خطوة من خطوات البيئة.

دعنا نتحدث بمزيد من التفاصيل حول كيف تبدو خطوة واحدة للتعلم هنا. نحن نفترض الآن أننا نخطو خطوة بخطوة عدد خطوات max_steps وحالة الحالة الحالية. ثم القيام بالعمل مع $$$\ varepsilon$السياسات الجشع ستبدو هكذا:

 epsilon = max_epsilon - (max_epsilon - min_epsilon)* step / max_steps action = select_action(state, epsilon, model) new_state, reward, done, _ = env.step(action) 

أضف على الفور التجربة المكتسبة إلى الذاكرة وبدء حلقة جديدة إذا انتهت الحالية:

 memory.push((state, action, reward, new_state, done)) if done: state = env.reset() done = False else: state = new_state 

وسنتخذ خطوة نزول التدرج (إذا ، بالطبع ، يمكننا بالفعل جمع دفعة واحدة على الأقل):

 if step > batch_size: fit(memory.sample(batch_size), model, target_model, optimizer) 

الآن يبقى تحديث target_model:

 if step % target_update == 0: target_model = copy.deepcopy(model) 

ومع ذلك ، نود أيضًا متابعة عملية التعلم. للقيام بذلك ، سنلعب حلقة إضافية بعد كل تحديث من target_model مع epsilon = 0 ، مع تخزين الجائزة الإجمالية في المخزن المؤقت rewards_by_target_updates:

 if step % target_update == 0: target_model = copy.deepcopy(model) state = env.reset() total_reward = 0 while not done: action = select_action(state, 0, target_model) state, reward, done, _ = env.step(action) total_reward += reward done = False state = env.reset() rewards_by_target_updates.append(total_reward) 

شغّل هذا الرمز واحصل على شيء مثل هذا الرسم البياني:

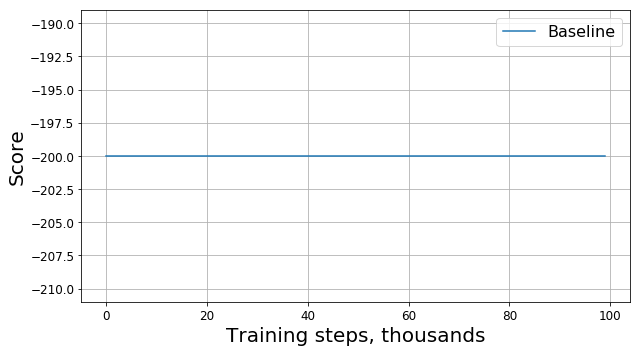
ما الخطأ الذي حدث؟

هل هذا خطأ؟ هل هذه خوارزمية خاطئة؟ هل هذه المعلمات سيئة؟ ليس حقا في الواقع ، المشكلة في المهمة ، وهي وظيفة المكافأة. دعونا ننظر في الأمر عن كثب. في كل خطوة ، يحصل وكيلنا على مكافأة -1 ، ويحدث هذا حتى تنتهي الحلقة. هذه المكافأة تحفز الوكيل على إكمال الحلقة في أسرع وقت ممكن ، ولكن في نفس الوقت لا يخبره كيف يفعل ذلك. ولهذا السبب ، فإن الطريقة الوحيدة لتعلم كيفية حل مشكلة في مثل هذه التركيبة للعامل هي حلها عدة مرات باستخدام الاستكشاف.

بالطبع ، يمكن للمرء محاولة استخدام خوارزميات أكثر تعقيدًا لدراسة البيئة بدلاً من بيئتنا $$$\ varepsilon$سياسات الجشع. ومع ذلك ، أولاً ، نظرًا لتطبيقها ، سيصبح نموذجنا أكثر تعقيدًا ، والذي نود تجنبه ، وثانياً ، ليس حقيقة أنها ستعمل بشكل جيد بما يكفي لهذه المهمة. بدلاً من ذلك ، يمكننا إزالة مصدر المشكلة عن طريق تعديل المهمة نفسها ، أي عن طريق تغيير وظيفة المكافأة ، أي عن طريق تطبيق ما يسمى تشكيل مكافأة.

تسريع التقارب

تخبرنا معرفتنا البديهية أنه لرفع التل تحتاج إلى تسريع. كلما زادت السرعة ، كلما اقترب الوكيل من حل المشكلة. يمكنك إخباره بذلك ، على سبيل المثال ، بإضافة وحدة سرعة مع معامل معين للمكافأة:

  معدل التعديل = المكافأة + 10 * القيمة المطلقة (new_state [1]) 

وفقا لذلك ، خط في وظيفة تناسب

  memory.push ((الحالة ، الإجراء ، المكافأة ، new_state ، تم التنفيذ)) 

يجب استبداله بـ

  memory.push ((الحالة ، الإجراء ، معدل_المصدر ، new_state ، المنجز)) 

الآن دعونا نلقي نظرة على المخطط الجديد (يقدم الجائزة الأصلية دون تعديلات):


هنا RS هي اختصار لتشكيل مكافأة.

هل من الجيد القيام بذلك؟

التقدم واضح: تعلم وكيلنا بوضوح رفع التل ، حيث بدأت الجائزة تختلف عن -200. لا يتبقى سوى سؤال واحد: إذا غيرنا وظيفة المكافأة ، فقد غيرنا المهمة نفسها أيضًا ، فهل سيكون حل المشكلة الجديدة التي وجدناها جيدًا للمشكلة القديمة؟

بادئ ذي بدء ، نحن نفهم ماذا يعني "الخير" في حالتنا. لحل المشكلة ، نحاول إيجاد السياسة المثلى - السياسة التي تزيد المكافأة الإجمالية للحلقة إلى الحد الأقصى. في هذه الحالة ، يمكننا استبدال كلمة "جيد" بكلمة "الأمثل" ، لأننا نبحث عنها. نأمل أيضًا بتفاؤل أن يجد DQN لدينا عاجلاً أم آجلاً الحل الأمثل للمشكلة المعدلة ، وأن لا تتعطل عند الحد الأقصى المحلي. لذا ، يمكن إعادة صياغة السؤال على النحو التالي: إذا غيرنا وظيفة المكافأة ، فقد غيّرنا المشكلة نفسها أيضًا ، فهل سيكون الحل الأمثل للمشكلة الجديدة التي وجدناها هو الحل الأمثل للمشكلة القديمة؟

كما اتضح ، لا يمكننا تقديم مثل هذا الضمان في الحالة العامة. تعتمد الإجابة على كيف قمنا بتغيير وظيفة المكافأة بالضبط ، وكيف تم ترتيبها مسبقًا وكيف يتم ترتيب البيئة نفسها. لحسن الحظ ، هناك مقال قام مؤلفوه بالتحقيق في كيفية تأثير تغيير وظيفة المكافأة على درجة الكمال في الحل الموجود.

أولاً ، وجدوا فئة كاملة من التغييرات "الآمنة" التي تستند إلى الطريقة المحتملة: $$$R '= R + (\ gamma \ cdot \ Phi (new \ _state) - \ Phi (state))$حيث $$$\ Phi$- المحتملة ، والتي تعتمد فقط على الدولة. لمثل هذه الوظائف ، تمكن المؤلفون من إثبات أنه إذا كان حل المشكلة الجديدة هو الحل الأمثل ، فإن المشكلة القديمة هي الحل الأمثل.

ثانياً ، أظهر المؤلفون ذلك لأي شخص آخر $$$R '= R + F (s، a)$هناك مثل هذه المشكلة ، وظيفة المكافأة R ، والحل الأمثل للمشكلة التي تم تغييرها ، أن هذا الحل ليس الأمثل للمشكلة الأصلية. هذا يعني أنه لا يمكننا ضمان جودة الحل الذي وجدناه إذا استخدمنا تغييرًا لا يعتمد على الطريقة المحتملة.

وبالتالي ، فإن استخدام الوظائف المحتملة لتعديل دالة المكافأة يمكن أن يغير فقط معدل تقارب الخوارزمية ، لكنه لا يؤثر على الحل النهائي.

تسريع التقارب بشكل صحيح

الآن بعد أن عرفنا كيفية تغيير المكافأة بأمان ، دعونا نحاول تعديل المهمة مرة أخرى ، باستخدام الطريقة المحتملة بدلاً من الاستدلال الساذج:

  معدل التعديل = المكافأة + 300 * (جاما * القيمة المطلقة (new_state [1]) - القيمة المطلقة (الحالة [1])) 

دعونا نلقي نظرة على الجدول الزمني للجائزة الأصلية:



كما اتضح فيما بعد ، بالإضافة إلى وجود ضمانات نظرية ، فإن تعديل المكافأة بمساعدة الوظائف المحتملة قد أدى أيضًا إلى تحسن كبير في النتيجة ، لا سيما في المراحل المبكرة. بالطبع ، هناك فرصة أنه سيكون من الممكن اختيار مزيد من المعلمات الفائقة (البذور العشوائية ، جاما ، وغيرها من المعاملات) لتدريب العامل ، ولكن تشكيل المكافآت مع ذلك يزيد بشكل كبير من معدل تقارب النموذج.

خاتمة

شكرا لك على القراءة حتى النهاية! آمل أن تكونوا قد استمتعت بهذه الرحلة الموجهة نحو الممارسة في التعلم المعزز. من الواضح أن ماونتين كار مهمة "لعبة" ، ولكن ، كما استطعنا أن نلاحظ ، أن تعليم وكيل لحل حتى هذه المهمة التي تبدو بسيطة من وجهة نظر إنسانية يمكن أن يكون صعباً.