كبير يا

المذكرة. ترجمة مختصرة ، بدلاً من إعادة سردها بكلماتك الخاصة.
محدث: كما هو موضح في التعليقات ، فإن الأمثلة ليست مثالية. لا يبحث المؤلف عن أفضل حل للمشكلة ، فهدفه هو شرح مدى تعقيد الخوارزميات "على الأصابع".

هناك حاجة إلى تدوين كبير O لوصف تعقيد الخوارزميات. لهذا ، يتم استخدام مفهوم الوقت. هذا الموضوع مخيف بالنسبة للكثيرين ، والمبرمجون الذين يتجنبون التحدث عن "وقت الترتيب N" أمر شائع.

إذا كنت قادرًا على تقييم الكود من حيث Big O ، فمن المرجح أنك تعتبر "رجل ذكي". وعلى الأرجح سوف تذهب من خلال المقابلة القادمة. لن تتوقف عن السؤال عما إذا كان من الممكن تقليل تعقيد قطعة من التعليمات البرمجية إلى n تسجيل الدخول مقابل n ^ 2.

هياكل البيانات

يعتمد اختيار بنية البيانات على المهمة المحددة: على نوع البيانات والخوارزمية لمعالجتها. تم إنشاء مجموعة متنوعة من بنيات البيانات (في .NET أو Java أو Elixir) لأنواع معينة من الخوارزميات.

في كثير من الأحيان ، باختيار بنية أو أخرى ، نقوم ببساطة بنسخ الحل المقبول عمومًا. في معظم الحالات ، هذا يكفي. ولكن في الواقع ، دون فهم تعقيد الخوارزميات ، لا يمكننا اتخاذ خيار مستنير. لا يمكن تمرير موضوع بنيات البيانات إلا بعد تعقيد الخوارزميات.

سنستخدم هنا صفيفات من الأرقام فقط (كما في مقابلة). أمثلة جافا سكريبت.

لنبدأ بالأبسط: O (1)

خذ مجموعة من 5 أرقام:

const nums = [1,2,3,4,5]; 

افترض أنك بحاجة للحصول على العنصر الأول. نستخدم الفهرس لهذا:

 const nums = [1,2,3,4,5]; const firstNumber = nums[0]; 

ما مدى تعقيد هذه الخوارزمية؟ يمكننا أن نقول: "ليست معقدة على الإطلاق - فقط تأخذ العنصر الأول من مجموعة". هذا صحيح ، لكن من الأصح وصف التعقيد من خلال عدد العمليات المنجزة لتحقيق النتيجة ، حسب المدخلات ( عمليات الإدخال).

بمعنى آخر: عدد العمليات التي ستزيد مع زيادة عدد معلمات الإدخال.

في مثالنا ، هناك 5 معلمات إدخال ، لأن هناك 5 عناصر في الصفيف. للحصول على النتيجة ، تحتاج إلى إجراء عملية واحدة (خذ عنصرًا بفهرس). كم عدد العمليات المطلوبة إذا كان هناك 100 عنصر في الصفيف؟ أو 1000؟ أو 100000؟ كل نفس ، هناك حاجة إلى عملية واحدة فقط.

وهذا هو: "عملية واحدة لجميع بيانات الإدخال الممكنة" - O (1).

يمكن قراءة O (1) كـ "تعقيد الطلب 1" (الترتيب 1) ، أو "الخوارزمية تعمل في وقت ثابت / ثابت" (وقت ثابت).

لقد خمنت بالفعل أن خوارزميات O (1) هي الأكثر كفاءة.

التكرار و "وقت الطلب n": O (n)

الآن دعونا نجد مجموع عناصر المصفوفة:

 const nums = [1,2,3,4,5]; let sum = 0; for(let num of nums){ sum += num; } 

مرة أخرى نسأل أنفسنا: كم عدد عمليات الإدخال التي نحتاجها؟ هنا تحتاج إلى فرز جميع العناصر ، أي العملية على كل عنصر. أكبر مجموعة ، والمزيد من العمليات.

باستخدام تدوين Big O: O (n) أو "تعقيد الترتيب n (order n)". أيضًا ، يسمى هذا النوع من الخوارزميات "خطي" أو أن الخوارزمية "تحجيمًا خطيًا".

تحليل

هل يمكننا أن نجعل الجمع أكثر كفاءة؟ عموما لا. وإذا علمنا أن الصفيف مكفول للبدء في 1 ، وفرزها وليس لديه فجوات؟ ثم يمكننا تطبيق المعادلة S = n (n + 1) / 2 (حيث n هو العنصر الأخير في المصفوفة):

 const sumContiguousArray = function(ary){ //get the last item const lastItem = ary[ary.length - 1]; //Gauss's trick return lastItem * (lastItem + 1) / 2; } const nums = [1,2,3,4,5]; const sumOfArray = sumContiguousArray(nums); 

هذه الخوارزمية أكثر فعالية بكثير من O (n) ، علاوة على ذلك ، يتم تنفيذها في "وقت ثابت / ثابت" ، أي هو يا (1).

في الواقع ، هناك أكثر من عملية واحدة: تحتاج إلى الحصول على طول الصفيف ، والحصول على العنصر الأخير ، وإجراء الضرب والقسمة. أليس هذا يا (3) أم شيء؟ في تدوين Big O ، العدد الفعلي للخطوات غير مهم ، من المهم أن يتم تشغيل الخوارزمية في وقت ثابت.

خوارزميات الوقت الثابت هي دائمًا O (1). الشيء نفسه مع الخوارزميات الخطية ، في الواقع ، يمكن أن تكون العمليات O (n + 5) ، في Big O ، التدوين هو O (n).

ليست أفضل الحلول: O (n ^ 2)

دعنا نكتب وظيفة تتحقق من الصفيف بحثًا عن التكرارات. حل حلقة المتداخلة:

 const hasDuplicates = function (num) { //loop the list, our O(n) op for (let i = 0; i < nums.length; i++) { const thisNum = nums[i]; //loop the list again, the O(n^2) op for (let j = 0; j < nums.length; j++) { //make sure we're not checking same number if (j !== i) { const otherNum = nums[j]; //if there's an equal value, return if (otherNum === thisNum) return true; } } } //if we're here, no dups return false; } const nums = [1, 2, 3, 4, 5, 5]; hasDuplicates(nums);//true 

نحن نعلم بالفعل أن التكرار الصفيف هو O (ن). لدينا حلقة متداخلة ، لكل عنصر نكرره مرة أخرى - أي O (n ^ 2) أو "تعقيد ترتيب n square."

الخوارزميات ذات الحلقات المتداخلة على نفس المجموعة تكون دائمًا O (n ^ 2).

"تعقيد ترتيب السجل n": O (log n)

في المثال أعلاه ، فإن الحلقة المتداخلة ، في حد ذاتها (إذا كنت لا تأخذ في الاعتبار أنها متداخلة) ، فإن التعقيد O (n) ، لأنه إنه تعداد عناصر الصفيف. تنتهي هذه الدورة بمجرد العثور على العنصر المطلوب ، أي في الواقع ، لن يتم تعداد جميع العناصر. لكن تدوين Big O يعتبر دائمًا أسوأ السيناريوهات - العنصر الذي تبحث عنه قد يكون الأخير.

هنا ، يتم استخدام حلقة متداخلة للبحث عن عنصر معين في صفيف. يمكن تحسين البحث عن عنصر في صفيف ، في ظل ظروف معينة ، بشكل أفضل من الخطي O (n).

دع المصفوفة مرتبة بعد ذلك ، يمكننا استخدام خوارزمية البحث الثنائي: قسّم المصفوفة إلى نصفين ، وتجاهلها غير الضرورية ، وقسم الباقي مرة أخرى إلى قسمين ، وهكذا حتى نجد القيمة المطلوبة. ويسمى هذا النوع من الخوارزمية divide و conquer Divide and Conquer.



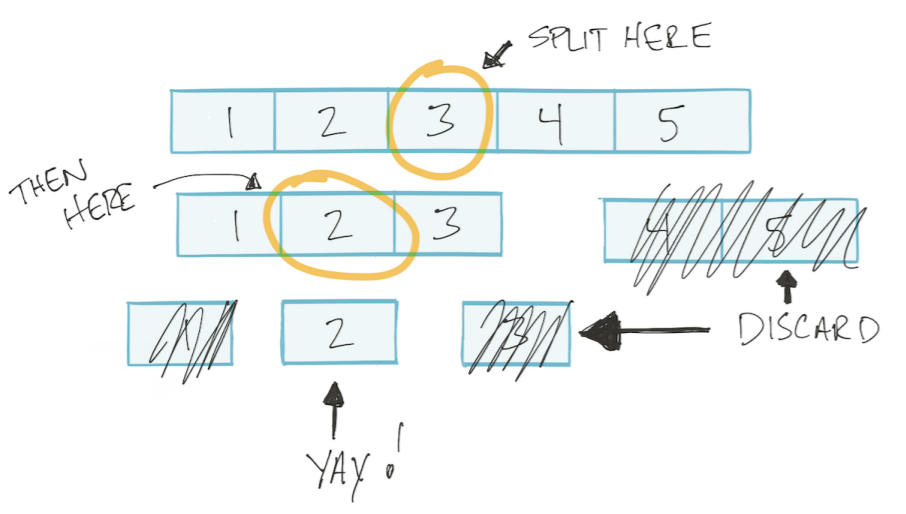
تستند هذه الخوارزمية إلى لوغاريتم.

نظرة عامة سريعة على اللوغاريتمات

خذ مثالاً ، ماذا سيكون x مساوياً؟

س ^ 3 = 8

نحتاج إلى أخذ الجذر التكعيبي لـ 8 - سيكون ذلك 2. الآن أكثر صعوبة

2 ^ س = 512

باستخدام اللوغاريتم ، يمكن كتابة المشكلة باسم

log2 (512) = س

"اللوغاريتم الأساسي 2 لـ 512 هو x." انتبه إلى "القاعدة 2" ، أي نفكر في توأمتين - كم مرة تحتاج إلى ضرب 2 للحصول على 512.

في خوارزمية البحث الثنائي ، في كل خطوة نقسم الصفيف إلى جزأين.

إضافة بلدي. أي في أسوأ الحالات ، نقوم بالعديد من العمليات حيث يمكننا تقسيم الصفيف إلى جزأين. على سبيل المثال ، كم مرة يمكننا تقسيم مجموعة من 4 عناصر إلى جزأين؟ 2 مرات. ومجموعة من 8 عناصر؟ 3 مرات. أي عدد الأقسام / العمليات = log2 (n) (حيث n هو عدد العناصر في الصفيف).

اتضح أن اعتماد عدد العمليات على عدد عناصر الإدخال يوصف بأنه log2 (n)


وبالتالي ، باستخدام تدوين Big O ، خوارزمية البحث الثنائية لها تعقيد O (log n).

تحسين O (n ^ 2) إلى O (n log n)

دعنا نعود إلى مهمة التحقق من الصفيف بحثًا عن التكرارات. قمنا بالتكرار على كل عناصر المصفوفة ، ولكل عنصر تم التكرار مرة أخرى. لقد فعلوا يا (ن) داخل يا (ن) ، أي O (n * n) أو O (n ^ 2).

يمكننا استبدال الحلقة المتداخلة ببحث ثنائي *. أي علينا فقط المرور عبر جميع عناصر O (n) ، بداخلنا نفعل O (log n). اتضح O (n * log n) ، أو O (n log n).

 const nums = [1, 2, 3, 4, 5]; const searchFor = function (items, num) { //use binary search! //if found, return the number. Otherwise... //return null. We'll do this in a later chapter. } const hasDuplicates = function (nums) { for (let num of nums) { //let's go through the list again and have a look //at all the other numbers so we can compare if (searchFor(nums, num)) { return true; } } //only arrive here if there are no dups return false; } 

* الاهتمام ، من أجل تجنب البصمة . يعد استخدام البحث الثنائي للتحقق من مجموعة من التكرارات حلاً سيئًا. إنه يوضح فقط كيفية تقييم تعقيد الخوارزمية الموضحة في قائمة الأكواد أعلاه ، من حيث Big O. خوارزمية جيدة أو سيئة واحدة ليست مهمة لهذه المادة ؛ الرؤية مهمة.

التفكير من حيث Big O

• الحصول على عنصر المجموعة هو O (1). سواء أكان يتم الحصول عليها عن طريق الفهرس في صفيف ، أو عن طريق المفتاح في القاموس في تدوين Big O ، سيكون O (1)
• التكرار على مجموعة هو O (n)
• الحلقات المتداخلة على نفس المجموعة هي O (n ^ 2)
• قسّم وقهر دائمًا يا (log n)
• التكرارات التي تستخدم Divide and Conquer هي O (n log n)