الأخطاء المضمنة في النظام: دورها في الإحصاءات

في مقالة سابقة ، أشرت إلى مدى انتشار مشكلة إساءة استخدام المعيار t في المنشورات العلمية (وهذا ممكن فقط بسبب انفتاحها ، وما هي النفايات التي يتم إنشاؤها عند استخدامها في أي دورة ، أو تقارير ، أو مهام تدريب ، وما إلى ذلك - غير معروفة) . لمناقشة ذلك ، تحدثت عن أساسيات تحليل التباين ومستوى الأهمية α الذي حدده الباحث نفسه. لكن لفهم الصورة الكاملة للتحليل الإحصائي ، من الضروري التأكيد على عدد من الأشياء المهمة. وأهمها هو مفهوم الخطأ.

خطأ وتطبيق غير صحيح: ما هو الفرق؟

أي نظام مادي يحتوي على نوع من الخطأ ، عدم الدقة. في الشكل الأكثر تنوعا: ما يسمى التسامح - الفرق في حجم المنتجات المختلفة من نفس النوع ؛ خاصية غير خطية - عندما يقيس الجهاز أو الطريقة شيئًا ما وفقًا لقانون معروف في حدود معينة ، ثم يصبح غير قابل للتطبيق ؛ السلطة التقديرية - عندما نكون غير قادرين تقنيًا على ضمان خاصية إخراج سلسة.

وفي الوقت نفسه ، هناك خطأ بشري محض - الاستخدام غير الصحيح للأجهزة والأدوات والقوانين الرياضية. هناك فرق جوهري بين الخطأ المتأصل في النظام والخطأ في تطبيق هذا النظام. من المهم التمييز بين هذين المفهومين وعدم الخلط بينهما فيما يطلق عليهما نفس الكلمة "خطأ". في هذه المقالة ، أفضل استخدام كلمة "خطأ" للإشارة إلى خصائص النظام و "الاستخدام غير الصحيح" - للاستخدام الخاطئ.

أي أن خطأ المسطرة مساوٍ لتسامح المعدات ، مما يضع حدودًا على قماشه. قد يكون الخطأ في الاستخدام غير الصحيح هو استخدامه عند قياس تفاصيل الساعة. تم كتابة خطأ الشراع على ذلك ويبلغ حجمه حوالي 50 جرامًا ، وستكون إساءة استخدام الشراع هو وزن كيس يبلغ وزنه 25 كجم ، والذي يمتد الربيع من منطقة قانون هوك إلى منطقة التشوهات البلاستيكية. ينبع خطأ مجهر القوة الذرية من سلطته التقديرية - لا يمكنك "لمس" الأجسام باستخدام مسبار أصغر من قطر ذرة واحدة. ولكن هناك العديد من الطرق لإساءة استخدامها أو إساءة تفسير البيانات. و هكذا.

لذا ، ما نوع الخطأ الذي يحدثه ذلك في الطرق الإحصائية؟ وهذا الخطأ هو بالضبط مستوى السمعة السيئة من الأهمية α.

أخطاء من النوع الأول والثاني

خطأ في جهاز الإحصاء الرياضي هو جوهره الاحتمالي بايزي نفسه. في المقالة الأخيرة ، أشرت بالفعل إلى الأساليب الإحصائية التي تستند إلى: تحديد مستوى الأهمية α باعتباره أكبر احتمال مقبول لرفض الفرضية بشكل غير قانوني ، والباحث عن تخصيص هذه القيمة بشكل مستقل للباحث.
هل ترى بالفعل هذه الاتفاقية؟ في الواقع ، في أساليب المعايير لا يوجد أي صرامة رياضية مألوفة. الرياضيات تعمل على الخصائص الاحتمالية.
وهنا تأتي نقطة أخرى حيث يمكن تفسير خاطئ لكلمة واحدة في سياق مختلف. من الضروري التمييز بين مفهوم الاحتمال والتنفيذ الفعلي لحدث ما ، معبراً عنه في توزيع الاحتمال. على سبيل المثال ، قبل البدء في أي من تجاربنا ، لا نعرف نوع القيمة التي سنحصل عليها نتيجة لذلك. هناك نتيجتان محتملتان: بعد تحديد قيمة معينة للنتيجة ، إما أننا سنحصل عليها بالفعل أم لا. من المنطقي أن يكون احتمال كلا الحدثين 1/2. لكن منحنى الجاوس الموضح في المقالة السابقة يوضح توزيع الاحتمالات الذي نخمنه بالصدفة.

يمكنك توضيح ذلك بوضوح مع مثال. دعونا لفة النرد مرتين 600 مرة - العادية والغش. نحصل على النتائج التالية:



قبل التجربة ، سيكون فقدان أي وجه لكلا المكعبين متساويًا - 1/6. ومع ذلك ، بعد التجربة ، يظهر جوهر مكعب الغش ، ويمكننا القول أن كثافة احتمال الستة التي تقع عليه تبلغ 90 ٪.

مثال آخر يعرفه الكيميائيون والفيزيائيون وأي شخص مهتم بالتأثيرات الكمية هو المدارات الذرية. من الناحية النظرية ، يمكن "تلطيخ" الإلكترون في الفضاء وتحديد موقعه في أي مكان تقريبًا. ولكن في الممارسة العملية ، هناك مجالات سيكون فيها 90 في المائة أو أكثر من الحالات. هذه المناطق من الفضاء التي تشكلت على سطح مع كثافة احتمال للإلكترون هناك 90 ٪ هي المدارات الذرية الكلاسيكية في شكل كرات ، الدمبل ، الخ

لذلك ، من خلال تحديد مستوى الأهمية بشكل مستقل ، نوافق على الخطأ الموصوف باسمه. لهذا السبب ، لا يمكن اعتبار نتيجة واحدة "موثوقة تمامًا" - دائمًا ستحتوي استنتاجاتنا الإحصائية على بعض الاحتمالات للفشل.

يسمى الخطأ الذي تم تحديده عن طريق تحديد مستوى الأهمية α خطأ من النوع الأول . يمكن تعريفها على أنها "إنذار خاطئ" ، أو ، بشكل صحيح ، نتيجة إيجابية خاطئة. في الواقع ، ماذا تعني عبارة "رفض الفرضية الخاطئة"؟ هذا يعني أخذ البيانات المرصودة عن طريق الخطأ للاختلافات الكبيرة بين المجموعتين. لإجراء تشخيص خاطئ حول وجود المرض ، والإسراع في الكشف عن اكتشاف جديد للعالم ، والذي لا وجود له بالفعل - هذه أمثلة على الأخطاء من النوع الأول.

ولكن بعد ذلك ، يجب أن تكون هناك نتائج سلبية كاذبة؟ صحيح تماما ، ويطلق عليهم أخطاء من النوع الثاني . الأمثلة هي تشخيص أو خيبة أمل في الوقت المناسب كنتيجة للدراسة ، رغم أنها في الواقع تحتوي على بيانات مهمة. يشار إلى الأخطاء من النوع الثاني بالحرف ، بشكل غريب بما فيه الكفاية ، β. لكن هذا المفهوم في حد ذاته ليس مهمًا بالنسبة للإحصاءات مثل الرقم 1-β. يُطلق على الرقم 1 power قوة المعيار ، وكما قد تتخيل ، فإنه يميز قدرة المعيار على عدم تفويت حدث مهم.
ومع ذلك ، فإن المحتوى في الأساليب الإحصائية للأخطاء من النوع الأول والثاني ليس فقط حدودها. يمكن استخدام مفهوم هذه الأخطاء في التحليل الإحصائي مباشرةً. كيف؟

تحليل ROC

تحليل ROC (من خاصية تشغيل المستقبل) هو طريقة لتحديد مدى قابلية تطبيق سمة معينة لتصنيف ثنائي للأجسام. ببساطة ، يمكننا التوصل إلى طريقة لتمييز المرضى عن الأشخاص الأصحاء ، والقطط من الكلاب ، والأسود من البيض ، ومن ثم التحقق من صحة هذه الطريقة. دعنا ننظر إلى مثال مرة أخرى.

اسمح لك أن تكون عالماً في الطب الشرعي الناشئ ، وأن تطور طريقة جديدة لتحديد ما إذا كان الشخص مجرمًا. لقد توصلت إلى علامة كمية: لتقييم الميول الإجرامية للأشخاص بتكرار الاستماع إلى ميخائيل كروغ. ولكن هل تعطي أعراضك نتائج كافية؟ هيا بنا
ستحتاج إلى مجموعتين من الأشخاص للتحقق من صحة معاييرك: المواطنون العاديون والمجرمون. في الواقع ، لنفترض أن متوسط ​​الوقت السنوي الذي يستمعون فيه إلى ميخائيل كروغ يختلف (انظر الشكل):



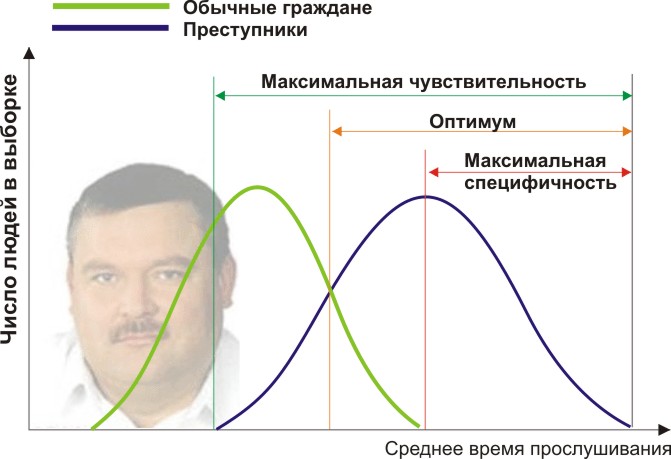
هنا نرى أنه من خلال الإشارة الكمية لوقت الاستماع ، تتقاطع عيناتنا. يستمع شخص ما إلى الدائرة تلقائيًا على الراديو دون ارتكاب جرائم ، وينتهك شخص ما القانون بالاستماع إلى الموسيقى الأخرى أو حتى الصم. ما هي شروط الحدود لدينا؟ يقدم تحليل ROC مفاهيم الانتقائية (الحساسية) والنوعية. تُعرَّف الحساسية بأنها القدرة على تحديد جميع النقاط التي تهمنا (في هذا المثال ، المجرمين) ، والخصوصية - عدم التقاط أي شيء إيجابي كاذب (عدم وضع السكان العاديين موضع شك). يمكننا تعيين بعض السمات الكمية المهمة التي تفصل بعضها عن غيرها (برتقالية) ، تتراوح من أقصى حساسية (خضراء) إلى أقصى خصوصية (أحمر).
دعونا نلقي نظرة على الرسم البياني التالي:



من خلال تحويل قيمة السمة الخاصة بنا ، نقوم بتغيير نسبة النتائج الإيجابية الكاذبة والسلبية الكاذبة (المنطقة الواقعة أسفل المنحنيات). بنفس الطريقة ، يمكننا تعريف الحساسية = الموضع. Res-t / (إيجابي Res-t + خطأ سالب. Res-t) وخصوصية = Neg. Res-t / (Res-t سالبة + موجبة خاطئة. Res-t).

ولكن الأهم من ذلك ، يمكننا تقييم نسبة النتائج الإيجابية إلى النتائج الإيجابية الخاطئة على كامل نطاق قيم السمة الكمية لدينا ، وهو منحنى ROC المطلوب لدينا (انظر الشكل):



وكيف نفهم من هذا الرسم البياني مدى جودة صفتنا؟ بسيط جدا ، احسب المساحة تحت المنحنى (AUC ، المساحة تحت المنحنى). الخط المتقطع (0،0 ؛ 1،1) يعني المصادفة الكاملة للعينين ومعيار لا معنى له تمامًا (المساحة تحت المنحنى هي 0.5 للمربع بأكمله). لكن محدب منحنى ROC يشير فقط إلى كمال المعيار. إذا نجحنا في العثور على معيار لا تتقاطع فيه العينات على الإطلاق ، فستشغل المنطقة الواقعة أسفل المنحنى الرسم البياني بأكمله. بشكل عام ، تعتبر السمة جيدة ، مما يسمح لأحد بفصل عينة واحدة عن الأخرى بشكل موثوق إذا كانت AUC> 0.75-0.8.

مع هذا التحليل ، يمكنك حل مجموعة متنوعة من المشاكل. بعد أن قررت أن عددًا كبيرًا من ربات البيوت كان موضع شك بسبب مايكل كروغ ، وبالإضافة إلى ذلك ، فقد تم إغفال المساعدين الخطرين الذين يستمعون إلى نوغانو ، يمكنك رفض هذا المعيار وتطوير معيار آخر.

بعد ظهوره كطريقة لمعالجة الإشارات اللاسلكية وتحديد "الصديق أو العدو" بعد الهجوم على بيرل هاربور (ومن هنا كان الاسم الغريب لخصائص المستقبِل) ، وجد تحليل ROC تطبيقًا واسعًا في إحصاءات الطب الحيوي للتحليل والتحقق من صحة وإنشاء وتوصيف لوحات العلامات البيولوجية إلخ أنها مرنة للاستخدام إذا كان يستند إلى منطق الصوت. على سبيل المثال ، يمكنك تطوير مؤشرات للفحص الطبي للمرضى الأساسيين المتقاعدين من خلال تطبيق معيار محدد للغاية ، وزيادة كفاءة الكشف عن أمراض القلب وعدم التحميل الزائد للأطباء مع المرضى غير الضروريين. وأثناء وباء خطير لفيروس غير معروف سابقًا ، على العكس من ذلك ، يمكنك التوصل إلى معيار انتقائي للغاية حتى لا يفلت أي شخص آخر من التطعيم.

التقينا بأخطاء من كلا النوعين ووضوحها في وصف المعايير التي تم التحقق منها. الآن ، بالانتقال من هذه الأسس المنطقية ، يمكننا تدمير سلسلة من الأوصاف النمطية النمطية الخاطئة للنتائج. بعض الصياغات غير الصحيحة تستحوذ على عقولنا ، وغالبًا ما تربكها كلماتها ومفاهيمها المتشابهة ، وأيضًا بسبب قلة الاهتمام بالتفسير الخاطئ. هذا ، ربما ، سوف تحتاج إلى أن تكون مكتوبة بشكل منفصل.