خوارزمية التثليث Delaunay عن طريق طريقة تجتاح الخط

يوم جيد!

في هذه المقالة ، سوف أصف بالتفصيل الخوارزمية التي حصلت عليها نتيجة لاستخدام فكرة "اكتساح الخط المستقيم" لبناء تثليث Delaunay على متن طائرة. هناك العديد من الأفكار التي لم أقابلها أبدًا عندما قرأت مقالات حول التثليث.
ربما شخص ما سيجدها أيضًا غير عادية. سأحاول أن أفعل كل شيء وفقًا لأفضل التقاليد وأن أدرج الأشياء التالية في القصة: وصف لهياكل البيانات المستخدمة ، ووصف لخطوات الخوارزمية ، وإثبات للصحة ، وتقديرات الوقت ، بالإضافة إلى مقارنة مع خوارزمية تكرارية باستخدام شجرة kD.

التعاريف وبيان المشكلة

التثليث

يقولون أن التثليث محدد على مجموعة النقاط على المستوى إذا كانت بعض أزواج النقاط متصلة بحافة ، وأي وجه محدد في الرسم البياني الناتج يشكل مثلثًا ، لا تتقاطع الحواف ، والرسم البياني هو الحد الأقصى في عدد الحواف.

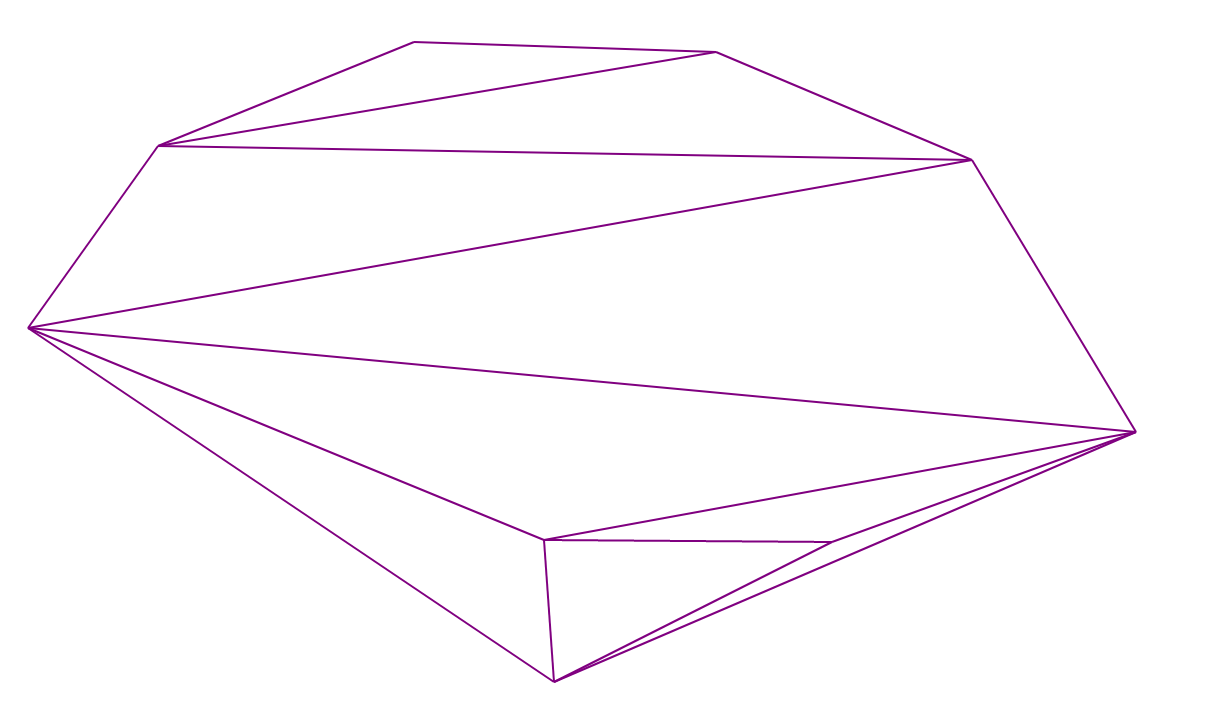
ديلوناي تثليث

تثليث Delaunay هو تثليث يكون فيه أي مثلث صحيحًا أنه لا توجد نقاط من المجموعة الأصلية داخل الدائرة المحددة حوله.

ملاحظة : بالنسبة لمجموعة معينة من النقاط التي لا توجد فيها 4 نقاط على نفس الدائرة ، يوجد تثليث Delaunay واحد تمامًا.

حالة ديلوناي

اسمحوا تعطى تثليث على مجموعة من النقاط. نقول أن مجموعة فرعية معينة من النقاط تلبي حالة Delaunay إذا كان التثليث المرتبط بهذه المجموعة الفرعية هو تثليث Delaunay بالنسبة له.

معيار التثليث ديلوناي

إن تحقيق شرط Delaunay لجميع النقاط التي تشكل رباعي الزوايا في التثليث يعادل حقيقة أن هذا التثليث هو تثليث Delaunay.

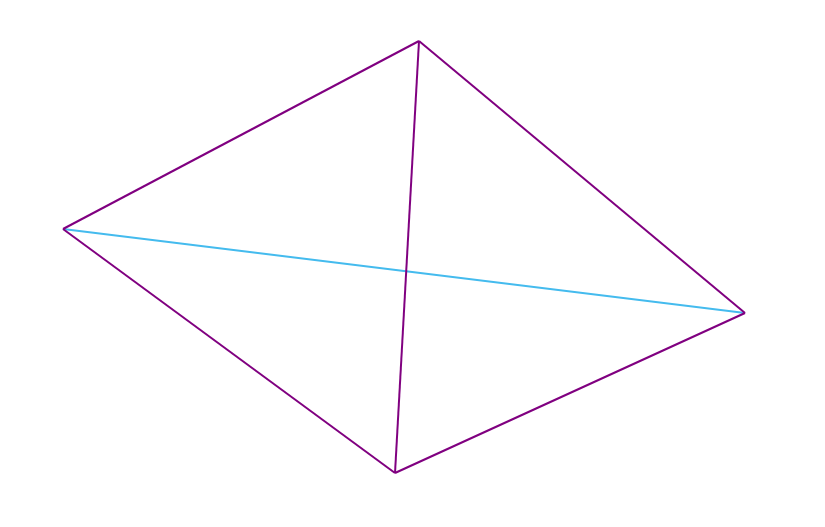
ملاحظة : بالنسبة للرباعيات غير المحدبة ، يتم دائمًا الوفاء بشرط Delaunay ، أما بالنسبة للرباعيات المحدبة (التي لا تقع رؤوسها على نفس الدائرة) فهناك بالضبط تثليثان محتملان (أحدهما تثليث Delaunay).

المهمة هي بناء تثليث Delaunay لمجموعة معينة من النقاط.

وصف الخوارزمية

نقاط مرئية وحواف مرئية

اترك الحد الأدنى المحدب من الهيكل (المشار إليه فيما يلي ، MBO) لمجموعة محددة من النقاط (حواف تربط بعض النقاط بحيث تشكل مضلعًا يحتوي على جميع نقاط المجموعة) ونقطة A تقع خارج الهيكل. ثم تُسمى نقطة المستوى بالنقطة A ، إذا كان المقطع الذي يربطها بالنقطة A لا يتقاطع مع MBO.

تسمى حافة MBO مرئية للنقطة A إذا كانت نهاياتها مرئية لـ A.

في الصورة التالية ، يتم وضع علامة على الحواف المرئية للنقطة الحمراء باللون الأحمر:

ملاحظة : كفاف Delaunay للتثليث هو MBO للنقاط التي تم تصميمه عليها.

الملاحظة 2 : في الخوارزمية ، تشكل الحواف المرئية للنقطة المضافة A سلسلة ، أي العديد من حواف MBO في صف واحد

تخزين التثليث في الذاكرة

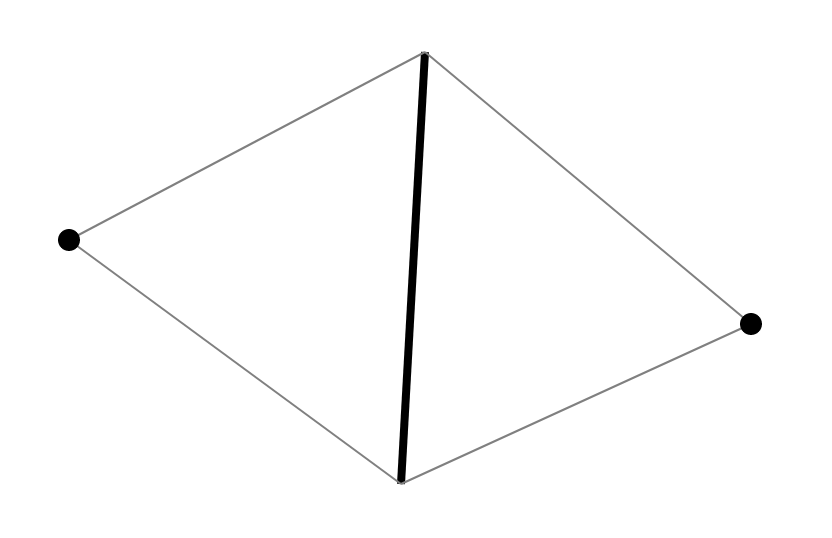
هناك بعض الطرق القياسية الموضحة جيدًا في كتاب Skvortsov [1]. بسبب تفاصيل الخوارزمية ، سأقدم روايتي الخاصة. نظرًا لأننا نريد التحقق من 4-gons لحالة Delaunay ، فإننا نعتبر هيكلها. كل رباعي الزوايا في التثليث هو مثلثان لهما حافة مشتركة. كل حافة لديها بالضبط 2 مثلثات مجاورة لها. وبالتالي ، يتم إنشاء كل رباعي الزوايا في التثليث من خلال حافة وقمتين مقابل الحافة في مثلثات متجاورة.
نظرًا لاستعادة مثلثين ومجاورتهما على طول الحافة والقمتين ، يمكننا استعادة التثليث لجميع هذه الهياكل. وفقًا لذلك ، يُقترح تخزين حافة ذات رأسين في المجموعة وإجراء بحث على طول الحافة (زوج مرتب من الرؤوس).

خوارزمية

فكرة الخط الكاسح هي أن جميع النقاط يتم فرزها في اتجاه واحد ، ومن ثم معالجتها بدورها.

1. فرز جميع النقاط على طول خط مستقيم (للبساطة ، عن طريق الإحداثيات $$$x$).
2. نحن نبني مثلثًا على أول 3 نقاط.
   
   علاوة على ذلك ، بالنسبة لكل نقطة تالية ، سنقوم بتنفيذ خطوات تحافظ على التغيير الثابت المتمثل في وجود تثليث Delaunay للنقاط التي تمت إضافتها بالفعل ، وبناءً على ذلك ، MBO بالنسبة لهم.
3. أضف المثلثات المكونة من الحواف المرئية والنقطة نفسها (أي ، أضف الحواف من النقطة المعنية إلى جميع أطراف الحواف المرئية).
4. نحن نتحقق من حالة Delaunay في كل المربعات التي تم إنشاؤها بواسطة الحواف المرئية. إذا لم يتم استيفاء الشرط في مكان ما ، فسنعيد بناء التثليث في الرباعي (أذكر أنه لا يوجد سوى اثنين منهم) ونعمل بشكل متكرر على التحقق من الزوايا الرباعية الناتجة عن حواف الرباعي الحالي (لأنه فقط بعدها يمكن انتهاك شرط Delaunay).

ملاحظة : في الخطوة (4) أثناء بداية العودية ، لا يمكنك التحقق من المربعات الرباعية التي تم إنشاؤها بواسطة الحواف القادمة من النقطة التي تم بحثها في هذا التكرار (هناك دائمًا اثنان من كل أربعة منها). غالبًا ما تكون غير محدبة ، لأن الإثبات محدب هندسي بحت ، سأتركه للقارئ. علاوة على ذلك ، نحن نفترض أنه يتم إجراء عمليتين متتاليتين فقط لكل عملية إعادة إنشاء.

التحقق من حالة ديلوناي

يمكن العثور على طرق اختبار رباعي الزوايا لحالة Delaunay في نفس الكتاب [1]. ألاحظ فقط أنه عند اختيار طريقة ذات وظائف مثلثية من هناك ، مع تنفيذ غير دقيق ، يمكن الحصول على القيم السلبية للجيوب ، فمن المنطقي أن نأخذها كموديل.

البحث عن الحواف المرئية

يبقى أن نفهم كيف نجد بفعالية الحواف المرئية. لاحظ أن النقطة المضافة السابقة S هي في MBO عند التكرار الحالي ، نظرًا لأن لديها أكبر إحداثي $$$x$، ويكون مرئيًا أيضًا للنقطة الحالية. بعد ذلك ، مع ملاحظة أن نهايات الحواف المرئية تشكل سلسلة مستمرة من النقاط المرئية ، يمكننا الانتقال من النقطة S في كلا الاتجاهين على طول MBO وجمع الحواف أثناء رؤيتها (يتم التحقق من رؤية الحافة باستخدام منتج المتجه). وبالتالي ، من الملائم تخزين MBO كقائمة متصلة على نحو مضاعف ، مع إزالة الحواف المرئية في كل تكرار وإضافة حرفين جديدين من النقطة المحددة.

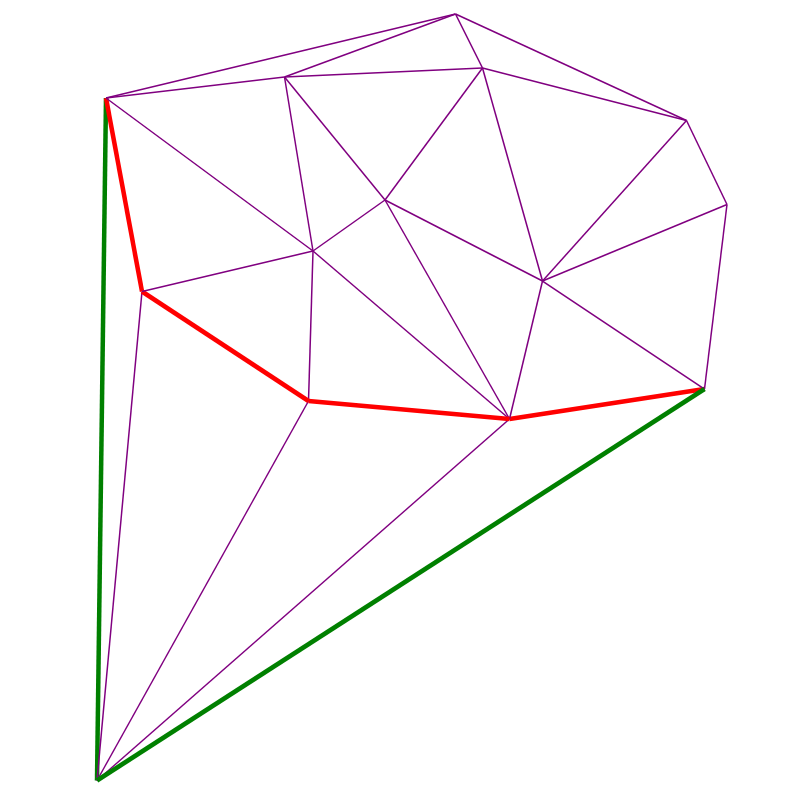
خوارزمية التصور

اثنين من النقاط الحمراء - أضيفت والسابقة. تشكل الحواف الحمراء في كل لحظة مكدس العودية من الخطوة (4):

صحة الخوارزمية

لإثبات صحة الخوارزمية ، يكفي إثبات الحفاظ على المتغير في الخطوتين (3) و (4).

الخطوة (3)

بعد الخطوة (3) ، من الواضح أننا نحصل على بعض التثليث لمجموعة النقاط الحالية.

الخطوة (4)

في عملية الخطوة (4) ، تكون جميع الزوايا الرباعية التي لا تفي بشرط Delaunay في مكدس العودية (يتبع من الوصف) ، مما يعني أنه في نهاية الخطوة (4) تفي جميع المربعات الربعية بشرط Delaunay ، أي ، يتم بناء تثليث Delaunay بالفعل. ثم يبقى إثبات أن العملية في الخطوة (4) ستنتهي يومًا ما. يأتي هذا من حقيقة أن جميع الحواف التي تمت إضافتها أثناء إعادة الإنشاء تأتي من القمة الحالية المعنية (أي في الخطوة $$$ك$لا يوجد أكثر من $$$ك -1 دولا$) ومن حقيقة أنه بعد إضافة هذه الحواف ، لن نأخذ في الاعتبار المربعات الرباعية التي أنشأتها (انظر الملاحظة السابقة) ، مما يعني أننا لن نضيف أكثر من مرة.

تعقيد الوقت

في المتوسط ​​، تعمل الخوارزمية جيدًا على التوزيعات العادية والموحدة (تظهر النتائج في الجدول أدناه). هناك افتراض أن وقت العمل هو $$$O (NlogN)$. في أسوأ الحالات ، يتم التقييم $$$O (N ^ 2)$.

دعونا نلقي نظرة على وقت العمل في أجزاء ونفهم أي واحد لديه أكبر تأثير على إجمالي الوقت:

الترتيب حسب الاتجاه

للفرز ، سوف نستخدم التقدير $$$O (NlogN)$.

البحث عن الحواف المرئية

أولاً ، نوضح أن إجمالي الوقت المستغرق في البحث عن الحواف المرئية هو $$$O (N)$. لاحظ أنه في كل تكرار ، نجد جميع الحواف المرئية و 2 أخرى (غير مرئية أولاً) في الوقت الخطي. في الخطوة (3) ، نضيف حواف جديدة إلى MBO. وهكذا ، في المجموع ، لا يزيد عن $$$2N$الأضلاع ، وبالتالي ، لن تكون الأضلاع المرئية المختلفة أكثر $$$2N$. سوف نجد أيضا $$$2N$حواف غير مرئية. وبالتالي ، في المجموع لم يعد هناك أكثر $$$4N دولا$الأضلاع التي تتوافق مع الوقت $$$O (N)$.

بناء مثلثات جديدة

من الواضح أن الوقت الإجمالي لبناء مثلثات من الخطوة (3) ذات حواف مرئية موجودة بالفعل $$$O (N)$.

إعادة بناء التثليث

يبقى أن نتعامل مع الخطوة (4). أولاً ، لاحظ أن التحقق من حالة Delaunay وإعادة البناء إذا لم يتم الوفاء بها يعد إجراءات مكلفة للغاية (على الرغم من أنها تعمل من أجلها) $$$O (1)$). فقط عند التحقق من حالة Delaunay يمكن أن يستغرق حوالي 28 عملية حسابية. لنلقِ نظرة على متوسط ​​عدد عمليات إعادة الإنشاء خلال هذه الخطوة. النتائج العملية لبعض التوزيعات مذكورة أدناه. بالنسبة إليهم ، أود حقًا أن أقول إن متوسط ​​عدد عمليات إعادة الترتيب ينمو بسرعة لوغاريتمية ، لكن دعنا نترك هذا بمثابة افتراض.

أود هنا أيضًا أن أشير إلى أن متوسط ​​عدد عمليات إعادة الترتيب لكل نقطة يمكن أن يختلف اختلافًا كبيرًا عن الاتجاه الذي يتم فيه إجراء الفرز. لذلك ، بالنسبة للمليون الموزع بالتساوي على مستطيل منخفض طويل مع نسبة عرض إلى ارتفاع 100000: 1 ، يختلف هذا الرقم من 1.2 إلى 24 (يتم تحقيق هذه القيم عند فرز البيانات أفقياً وعموديًا ، على التوالي). لذلك ، أرى النقطة في اختيار اتجاه الفرز بطريقة تعسفية (في هذا المثال ، مع الاختيار التعسفي ، تم الحصول على حوالي 2 عمليات إعادة بناء في المتوسط) أو تحديدها يدويًا إذا كانت البيانات معروفة مقدمًا.

وبالتالي ، فإن الوقت الرئيسي للبرنامج يأخذ عادة إلى الخطوة (4). إذا كان يعمل بسرعة ، فمن المنطقي أن نفكر في تسريع الفرز.

حالة أسوأ

حالة أسوأ على $$$ك$عشر يحدث التكرار $$$ك -1 دولا$الدعوة المتكررة في الخطوة (4) ، أي تلخيص كل شيء ، نحصل على السلوك المقارب في أسوأ الحالات $$$O (N ^ 2)$. توضح الصورة التالية مثالًا جميلًا يمكن للبرنامج أن يعمل عليه لفترة طويلة (1100 إعادة بناء في المتوسط ​​عند إضافة نقطة جديدة مع إدخال 10000 نقطة).

مقارنة مع خوارزمية تكرارية لبناء التثليث Delaunay باستخدام شجرة kD

وصف الخوارزمية التكرارية

سأصف بإيجاز الخوارزمية أعلاه. عندما تصل النقطة التالية ، نستخدم kD-tree (أنصحك أن تقرأ عنها في مكان ما ، إذا كنت لا تعرف) ، فنجد مثلثًا قريب جدًا منه بالفعل. بعد ذلك نتجاوز بحثًا عميقًا عن مثلث تسقط فيه النقطة نفسها. نمد الحواف إلى رؤوس المثلث الموجود وننفذ فعليًا الخطوة (4) من خوارزمية الخوارزميات الجديدة. نظرًا لأن النقطة يمكن أن تكون خارج التثليث ، من أجل التبسيط ، يُقترح أن تغطي جميع النقاط بمثلث كبير (لإنشائها مقدمًا) ، فإن هذا سيحل المشكلة.

تشابه الخوارزميات

في الواقع ، إذا تمت إضافة نقاط بالترتيب حسب الاتجاه ، فإن خوارزمية لدينا تعمل في الواقع بنفس الطريقة التكرارية ، باستثناء أن عدد عمليات إعادة الترتيب أقل. الرسوم المتحركة التالية توضح هذا تماما. على ذلك ، تمت إضافة نقاط من اليمين إلى اليسار ، وكلها مغطاة بمثلث كبير ، والذي تتم إزالته لاحقًا.

خوارزميات الاختلافات

في خوارزمية تكرارية ، يحدث تعريب نقطة (البحث عن المثلث المطلوب) في المتوسط ​​على مدى $$$O (logN)$، على التوزيعات أعلاه ، في المتوسط ​​، تحدث 3 عمليات إعادة ترتيب (كما هو موضح في [1]) بشرط وجود أمر تعسفي لتزويد النقاط. وهكذا ، فإن الخط الكاسح يفوز بوقت الخوارزمية التكرارية في التوطين ، لكنه يفقدها في عملية إعادة البناء (والتي ، على ما أذكر ، صعبة للغاية). بالإضافة إلى ذلك ، تعمل الخوارزمية التكرارية عبر الإنترنت ، والتي تعد أيضًا ميزتها المميزة.

استنتاج

أنا هنا أعرض بعض التثليثات المثيرة للاهتمام الناتجة عن تشغيل الخوارزمية.

نمط جميل

التوزيع الطبيعي ، 1000 نقطة

حتى التوزيع ، 1000 نقطة

التثليث مبني على مواقع جميع مدن روسيا

هنا يمكنك رؤية مثال على الكود الخاص بي لهذه الخوارزمية:
github.com/Vemmy124/Delaunay-Triangulation-Algorithm

شكرا لاهتمامكم!

أدب

[1] Skvortsov A.V. التثليث Delaunay وتطبيقه. - تومسك: دار النشر توم. الجامعة ، 2002. - 128 صفحة. ISBN 5-7511-1501-5