نحن منخرطون في شراء حركة المرور من Adwords (منصة إعلانية من Google). واحدة من المهام العادية في هذا المجال هو إنشاء لافتات جديدة. تُظهر الاختبارات أن الشعارات تفقد فعاليتها بمرور الوقت ، حيث يعتاد المستخدمون على الشعار ؛ الفصول والاتجاهات تتغير. بالإضافة إلى ذلك ، لدينا هدف لالتقاط منافذ جمهور مختلفة ، وتعمل اللافتات ذات الأهداف الضيقة بشكل أفضل.

فيما يتعلق بدخول بلدان جديدة ، نشأت مسألة توطين لافتات. لكل راية ، تحتاج إلى إنشاء إصدارات بلغات مختلفة وبعملات مختلفة. يمكنك أن تطلب من المصممين القيام بذلك ، ولكن هذا العمل اليدوي سيضيف عبئًا إضافيًا إلى مورد نادر بالفعل.

تبدو المهمة سهلة التشغيل الآلي. للقيام بذلك ، يكفي إنشاء برنامج يفرض على اللافتة سعرًا محليًا لـ "علامة السعر" وندعو إلى اتخاذ إجراء (عبارة مثل "اشتر الآن") على الزر. إذا كانت طباعة النص في صورة بسيطة بدرجة كافية ، فإن تحديد المكان الذي تحتاج إلى وضعه ليس تافها دائمًا. يضيف Peppercorns أن الزر يأتي بألوان مختلفة ، وهو مختلف قليلاً في الشكل.

هذه المقالة مخصصة لـ: كيفية العثور على الكائن المحدد في الصورة؟ سيتم فرز الطرق الشائعة. مجالات التطبيق ، والميزات ، إيجابيات وسلبيات. يمكن استخدام الطرق المذكورة أعلاه لأغراض أخرى: تطوير برامج للكاميرات الأمنية وأتمتة اختبار واجهة المستخدم وما شابه. يمكن العثور على الصعوبات الموضحة في مهام أخرى ، ويمكن استخدام الطرق المستخدمة لأغراض أخرى. على سبيل المثال ، غالبًا ما يتم استخدام Canny Edge Detector لتصنيع الصور مسبقًا ، ويمكن استخدام عدد نقاط المفاتيح لتقييم "التعقيد" المرئي للصورة.

آمل أن تغذي الحلول الموصوفة ترسانتك من الأدوات والحيل لحل المشاكل.

الكود موجود في Python 3.6 ( مستودع ) ؛ OpenCV مكتبة المطلوبة. من المتوقع أن يفهم القارئ أساسيات الجبر الخطي ورؤية الكمبيوتر.

سوف نركز على إيجاد الزر نفسه. سوف نتذكر كيفية العثور على علامات الأسعار (حيث يمكن أيضًا العثور على مستطيل بطرق أبسط) ، لكننا نتجاهله ، لأن الحل سيبدو بنفس الطريقة.

مطابقة القالب

الفكر الأول الذي يتبادر إلى الذهن هو لماذا لا تختار وتجد في الصورة المنطقة الأكثر تشابهاً بالزر من حيث اختلاف ألوان البكسل؟ هذا هو ما يجعل مطابقة القالب - طريقة تعتمد على إيجاد مساحة على الصورة تشبه القالب. يتم تعريف "تشابه" الصورة بمقياس معين. أي أن القالب "متراكب" على الصورة ، ويتم النظر في التناقض بين الصورة والقالب. موضع القالب الذي سيكون فيه هذا التناقض ضئيلًا وسيشير إلى موقع الكائن المطلوب.

يمكنك استخدام خيارات مختلفة كمقياس ، على سبيل المثال ، مجموع الفروق التربيعية بين القالب والصورة (مجموع الفروق التربيعية ، SSD) ، أو استخدام الارتباط المتبادل (CCORR). دع f و g هما الصورة والنمط بأبعاد (k ، l) و (m ، n) ، على التوالي (سوف نتجاهل قنوات الألوان في الوقت الحالي) ؛ أنا ، ي - وضع على الصورة التي "نعلق" القالب.

$$

$$SSD_ {i، j} = \ sum_ {a = 0..m، b = 0..n} {(f_ {i + a، j + b} - g_ {a، b}) ^ 2}$$

$$

$$CCORR_ {i، j} = \ sum_ {a = 0..m، b = 0..n} {(f_ {i + a، j + b} \ cdot g_ {a، b}) ^ 2}$$

دعونا نحاول تطبيق اختلاف المربعات لإيجاد قطة صغيرة

في الصورة

(الصورة مأخوذة من PETA رعاية القطط).

الصورة اليسرى هي القيمة المترية لتشابه المكان في الصورة مع القالب (أي قيم SSD لمختلف i، j). المنطقة المظلمة هي المكان الذي يوجد فيه الفرق ضئيل. هذا مؤشر إلى المكان الذي يشبه القالب - في الصورة الصحيحة ، هذا المكان محاط بدائرة.

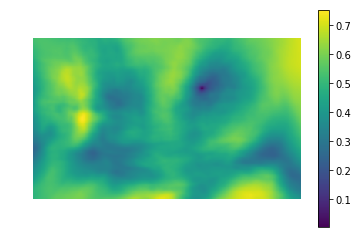
الارتباط المتبادل هو في الواقع مجموعة من صورتين. يمكن تنفيذ التلافيات بسرعة باستخدام تحويل فورييه السريع. وفقًا لنظرية الالتواء ، بعد تحويل فورييه ، يتحول الإلتواء إلى ضرب بسيط بعنصر أساسي:

$$

$$CCORR_ {i، j} = f \ circledast g = IFFT (FFT (f \ circledast g)) = IFFT (FFT (f) \ cdot FFT (g))$$

حيث $$$\ circledast$ - مشغل الإلتواء. بهذه الطريقة يمكننا حساب الارتباط المتبادل بسرعة. هذا يعطي التعقيد الكلي لـ O (kllog (kl) + mnlog (mn)) ، مقابل O (klmn) عند تنفيذه مباشرة. يمكن أيضًا تحقيق مربع الاختلاف باستخدام التحويل ، لأنه بعد فتح الأقواس ، سيتحول إلى الفرق بين مجموع مربعات قيم بكسل الصورة والترابط التبادلي:

$$

$$SSD_ {i، j} = \ sum_ {a = 0..m، b = 0..n} {(f_ {i + a، j + b} - g_ {a، b}) ^ 2} =$$

$$

$$= \ sum_ {a = 0..m، b = 0..n} {f_ {i + a، j + b} ^ 2 - 2 f_ {i + a، j + b} g_ {a، b} + g_ {a، b} ^ 2} =$$

$$

$$= \ sum_ {a = 0..m، b = 0..n} {f_ {i + a، j + b} ^ 2 + g_ {a، b} ^ 2} - 2CCOR_ {i، j}$$

يمكن رؤية التفاصيل في هذا العرض التقديمي .

دعنا ننتقل إلى التنفيذ. لحسن الحظ ، اعتنى بنا زملاؤنا من قسم نيجني نوفغورود إنتل عن طريق إنشاء مكتبة OpenCV ، وهو ينفذ بالفعل عملية بحث عن قالب باستخدام طريقة matchTemplate (بالمناسبة ، يستخدم تطبيق FFT ، على الرغم من أن هذا غير مذكور في الوثائق) ، باستخدام مقاييس تباين مختلفة :

• CV_TM_SQDIFF - مجموع مربعات الفرق في قيم البيكسل
• CV_TM_SQDIFF_NORMED - مجموع مربع الاختلافات اللون ، تطبيع إلى النطاق 0..1.
• CV_TM_CCORR - مجموع منتجات العناصر حسب العنصر للجزء القالب والصورة
• CV_TM_CCORR_NORMED - مجموع أعمال العنصر ، تم تطبيعه إلى النطاق -1..1.
• CV_TM_CCOEFF - الارتباط المتبادل للصور بدون متوسط
• CV_TM_CCOEFF_NORMED - الارتباط المتبادل بين الصور بدون متوسط ​​، عادي إلى -1..1 (ارتباط بيرسون)

سوف نستخدمها للعثور على القط الصغير:

يمكن ملاحظة أن TM_CCORR فقط لم يتعامل مع مهمته. هذا أمر مفهوم: نظرًا لأنه منتج عددي ، فإن أكبر قيمة لهذا المقياس ستكون عند مقارنة قالب بمستطيل أبيض.

قد تلاحظ أن هذه المقاييس تتطلب مطابقة لنمط البكسل في بكسل في الصورة المطلوبة. أي انحراف في غاما أو الضوء أو الحجم سيؤدي إلى طرق لا تعمل. اسمحوا لي أن أذكرك بأن هذا هو حالنا بالضبط: يمكن أن تكون الأزرار بأحجام مختلفة وألوان مختلفة.

يمكن حل مشكلة الألوان والضوء المختلفة عن طريق تطبيق مرشح للكشف عن الحواف. لا تترك هذه الطريقة سوى معلومات حول المكان الذي توجد به تغييرات الألوان الحادة في الصورة. لنستخدم تطبيق Canny Edge Detector (سنقوم بتحليله أكثر قليلاً) على الأزرار ذات الألوان المختلفة والسطوع. على اليسار توجد الشعارات الأصلية ، وعلى الجانب الأيمن نتيجة تطبيق مرشح Canny.

في حالتنا ، هناك أيضًا مشكلة ذات أحجام مختلفة ، ولكن تم حلها بالفعل. يحول التحويل إلى القطبية صورة إلى حيز يظهر فيه التكبير / التصغير ودوران إزاحة. باستخدام هذا التحول ، يمكننا استعادة النطاق وزاوية. بعد ذلك ، من خلال تحجيم القالب وتدويره ، يمكنك العثور على موضع القالب في الصورة الأصلية. يمكنك أيضًا استخدام FFT خلال هذا الإجراء ، كما هو موضح في تقنية تستند إلى FFT للترجمة ، والتناوب ، وتسجيل الصور على نطاق واسع . في الأدبيات ، يتم النظر في الحالة عند تغيير الأنماط الأفقية والعمودية بشكل متناسب ، في حين أن عامل المقياس يتغير ضمن حدود صغيرة (2.0 ... 0.8). لسوء الحظ ، يمكن أن يكون تغيير حجم زر كبيرًا وغير متناسب ، مما قد يؤدي إلى نتيجة غير صحيحة.

نحن نطبق الإنشاء الناتج (مرشح Canny ، الذي يستعيد فقط المقياس من خلال التحول اللوغاريتمي ، ونحصل على الوظيفة من خلال إيجاد المكان مع الحد الأدنى من التباين التربيعي) ، للعثور على الزر في ثلاث صور. سوف نستخدم الزر الأصفر الكبير كقالب:

في الوقت نفسه ، ستكون الأزرار الموجودة على اللافتات بأنواعها وألوانها وأحجامها المختلفة:

في حالة تغيير حجم الزر ، لم تنجح الطريقة بشكل صحيح. هذا يرجع إلى حقيقة أن الطريقة تنطوي على تغيير حجم الأزرار في نفس العدد من المرات أفقيا وعموديا. ومع ذلك ، هذا ليس هو الحال دائما. في الصورة الصحيحة ، لم يتغير حجم الزر عموديًا ، ولكن أفقياً انخفض بشكل كبير. إذا كان حجم التحجيم كبيرًا جدًا ، فإن التشوهات التي تسببها عملية التحول إلى القطبية تجعل البحث غير مستقر. في هذا الصدد ، لم تتمكن الطريقة من اكتشاف الزر في الحالة الثالثة.

كشف Keypoint

يمكنك تجربة طريقة مختلفة: بدلاً من البحث عن الزر بالكامل ، دعنا نعثر على أجزائه النموذجية ، على سبيل المثال ، زوايا الزر أو العناصر الحدودية (توجد حد زخرفي على طول محيط الزر). يبدو أن العثور على زوايا وحدود أسهل ، نظرًا لأن هذه الأشياء صغيرة (وبالتالي بسيطة). ما يكمن بين الزوايا الأربع والحدود سيكون زر. يُطلق على فئة أساليب البحث عن النقاط الرئيسية "اكتشاف النقاط الرئيسية" ، وتسمى خوارزميات المقارنة والبحث عن الصور باستخدام النقاط الأساسية "مطابقة النقاط الرئيسية". إن البحث عن نموذج في صورة ما يكمن في تطبيق خوارزمية للكشف عن النقاط الرئيسية لنمط وصورة ، ومقارنة النقاط الرئيسية لنمط وصورة.

عادةً ما يتم العثور على "النقاط الرئيسية" تلقائيًا من خلال البحث عن وحدات بكسل لها محيط معين. تم اختراع العديد من الطرق والمعايير للعثور عليها. كل هذه الخوارزميات هي استدلاليات تجد بعض عناصر الصورة المميزة ، كقاعدة عامة - زوايا أو تغيرات حادة في اللون. يجب أن يعمل كاشف جيد بسرعة ويكون مقاومًا لتحويلات الصورة (عند تغيير الصورة ، يجب ألا تتوقف النقاط الرئيسية عن الحركة / الحركة).

هاريس كاشف الزاوية

واحدة من أبسط الخوارزميات هو كاشف ركن هاريس . بالنسبة للصورة (فيما يلي ، نعتبر أننا نعمل "بكثافة" - صورة مترجمة إلى تدرج رمادي) ، يحاول العثور على نقاط في الجوار تكون فيها اختلافات الشدة أكبر من حد معين. تبدو الخوارزمية كما يلي:

1. من الشدة $$$I$ هي مشتقات على طول المحور ص و ( $$$I_x$ و $$$I_y$ على التوالي). يمكن العثور عليها ، على سبيل المثال ، من خلال تطبيق مرشح Sobel.

   
   

2. لبكسل ، والنظر في مربع $$$I_x$ مربع $$$I_y$ ويعمل $$$I_x$ و $$$I_y$ . بعض المصادر تسمية لهم $$$I_ {xx}$ . $$$I_ {xy}$ و $$$I_ {xy}$ - وهذا لا يضيف الوضوح ، حيث قد يظن المرء أن هذه هي المشتقات الثانية من الشدة (وهذا ليس كذلك).

   
   

3. لكل بكسل ، نأخذ في الاعتبار المبالغ الموجودة في حي معين (أكثر من 1 بكسل) بالخصائص التالية:

   $$

   $$A = \ sum_ {x، y} {w (x، y) I_xI_x}$$
   
   

   $$

   $$B = \ sum_ {x، y} {w (x، y) I_xI_y}$$
   
   

   $$

   $$C = \ sum_ {x، y} {w (x، y) I_yI_y}$$
   
   كما هو الحال في اكتشاف القوالب ، يمكن تنفيذ هذا الإجراء الخاص بالنوافذ الكبيرة بكفاءة باستخدام نظرية الالتواء.
   

4. لكل بكسل ، احسب القيمة $$$^ \ نجمة$ ارشادي ار

   $$

   $$R = Det (H) - k (Tr (H)) ^ 2 = (AB - C ^ 2) - k (A + B) ^ 2$$
   
   قيمة $$$ك$ تم اختيارها تجريبيا في النطاق [0.04 ، 0.06] إذا $$$R$ بعض بكسل لديه عتبة معينة ، ثم الحي $$$w$ يحتوي هذا البكسل على زاوية ، ونقوم بوضع علامة عليه كنقطة أساسية.
   

5. يمكن أن تنشئ الصيغة السابقة مجموعات من النقاط الرئيسية التي تقع بجانب بعضها البعض ، وفي هذه الحالة ، يجب أن تقوم بإزالتها. يمكن القيام بذلك عن طريق التحقق من كل نقطة سواء كان لها قيمة $$$R$ الحد الأقصى بين الجيران المباشرين. إذا لم يكن كذلك ، فسيتم تصفية النقطة الرئيسية. هذا الإجراء يسمى الحد الأقصى للقمع .

   
   

$$$\ نجمة$ صيغة $$$R$ اختير لسبب ما. $$$A ، B ، C$ - مكونات الموتر الهيكلي - مصفوفة تصف سلوك التدرج في الحي:

$$

$$H = \ تبدأ {pmatrix} A & C \\ C & B \ end {pmatrix}$$

تشبه هذه المصفوفة من نواح كثيرة مصفوفة التغاير. على سبيل المثال ، كلاهما مصفوفات شبه إيجابية بشكل إيجابي ، لكن التشابه لا يقتصر على هذا. اسمحوا لي أن أذكركم بأن مصفوفة التغاير لها تفسير هندسي. تشير متجهات التهيئة الذاتية لمصفوفة التغاير إلى اتجاهات التباين الأكبر لبيانات المصدر (التي تم حساب التباين) ، وتشير القيم المتجانسة إلى التشتت على طول المحور:

الصورة مأخوذة من http://www.visiondummy.com/2014/04/geometric-interpretation-covariance-matrix/

تتصرف القيم الذاتية للمنسق الهيكلي أيضًا بنفس الطريقة: فهي تصف انتشار التدرجات. على سطح مستو ، ستكون القيم الذاتية للمكورس الهيكلي صغيرة (لأن انتشار التدرجات نفسها سيكون صغيراً). تختلف القيم الذاتية للمنسق الهيكلي المبنية على قطعة من الصورة ذات الوجه اختلافًا كبيرًا: سيكون الرقم واحدًا كبيرًا (ويتوافق مع ناقله الموجه عموديًا على الوجه) ، والثاني سيكون صغيرًا. على موتر الزاوية ، ستكون القيم الذاتية كبيرة. بناءً على ذلك ، يمكننا بناء مجريات الأمور ( $$$\ lambda_1 ، \ lambda_2$ هي القيم الذاتية للمنسق الهيكلي).

$$

$$R = \ lambda_1 \ lambda_2 - k (\ lambda_1 + \ lambda_2) ^ 2$$

ستكون قيمة هذا الكشف عن مجريات الأمور كبيرة عندما تكون كل القيم الذاتية كبيرة.

مجموع القيم الذاتية هو تتبع المصفوفة ، والذي يمكن حسابه كمجموع للعناصر في القطر (وإذا نظرت إلى الصيغتين A و B ، يصبح من الواضح أن هذا هو مجموع مربعات أطوال التدرجات في المنطقة):

$$

$$\ lambda_1 + \ lambda_2 = Tr (H) = A + B$$

يُعد ناتج القيم الذاتية محددًا للمصفوفة ، والتي يسهل أيضًا كتابتها في حالة 2x2:

$$

$$\ lambda_1 \ lambda_2 = Det (H) = AB - C ^ 2$$

وبالتالي ، يمكننا حساب فعال $$$R$ ، معبراً عنها من حيث مكونات التينور الهيكلي.

FAST

طريقة هاريس جيدة ، ولكن هناك العديد من البدائل لها. لن نفكر في كل شيء بنفس الطريقة الموضحة أعلاه ، ولن نذكر سوى القليل منها لإظهار الحيل المثيرة للاهتمام ومقارنتها في العمل.

تم التحقق من البكسل بواسطة خوارزمية FAST

بديل لطريقة هاريس هو FAST . كما يوحي الاسم ، فاست أسرع بكثير من الطريقة المذكورة أعلاه. تحاول هذه الخوارزمية العثور على النقاط التي تقع على حواف وزوايا الكائنات ، أي في أماكن اختلاف التباين. موقعها كالتالي: تقوم FAST بإنشاء دائرة نصف قطرها R حول بكسل المرشح والتحقق مما إذا كانت تحتوي على شريحة مستمرة من البكسل بطول t تكون أغمق (أو أفتح) في بكسل المرشح بوحدات K. إذا تم استيفاء هذا الشرط ، فسيتم اعتبار البيكسل "نقطة أساسية". بالنسبة إلى t ، يمكننا تنفيذ هذا الكشف عن مجريات الأمور بكفاءة عن طريق إضافة عدد قليل من الاختبارات الأولية التي ستقطع البيكسلات المضمونة لتكون غير زوايا. على سبيل المثال ، متى $$$R = 3 دولا$ و $$$t = 12$ ، يكفي التحقق مما إذا كانت هناك 3 وحدات بكسل متتالية بين وحدات البكسل القصوى الأربعة التي تكون أغمق / أفتح تمامًا من المركز على K (في الصورة - 1 ، 5 ، 9 ، 13). يسمح لك هذا الشرط بقص المرشحين الذين لا يمثلون نقاطًا أساسية.

فرزت

كلا الخوارزميات السابقة ليست مقاومة لتغيير حجم الصورة. لا يسمحون لك بالعثور على قالب في الصورة إذا تم تغيير حجم الكائن. يوفر SIFT (تحويل ميزة تغيير المقياس) حلاً لهذه المشكلة. التقط الصورة التي نستخرج منها النقاط الرئيسية ، وابدأ في تقليل حجمها تدريجياً بخطوة صغيرة ، ولكل خيار مقياس ، سنجد النقاط الأساسية. التحجيم هو إجراء صعب ، لكن تقليله بمقدار 2/4/8 / ... يمكن القيام به بكفاءة عن طريق تخطي وحدات البكسل (في SIFT تسمى هذه المقاييس المتعددة "octaves"). يمكن تقريب المقاييس الوسيطة من خلال تطبيق bluss Gaussian بحجم أساسي مختلف على الصورة. كما ذكرنا أعلاه ، يمكن أن يتم ذلك حسابياً بكفاءة. ستبدو النتيجة إذا قمنا بتقليل الصورة لأول مرة ثم قمنا بتكبيرها بحجمها الأصلي - يتم فقد التفاصيل الصغيرة ، تصبح الصورة "غير واضحة".

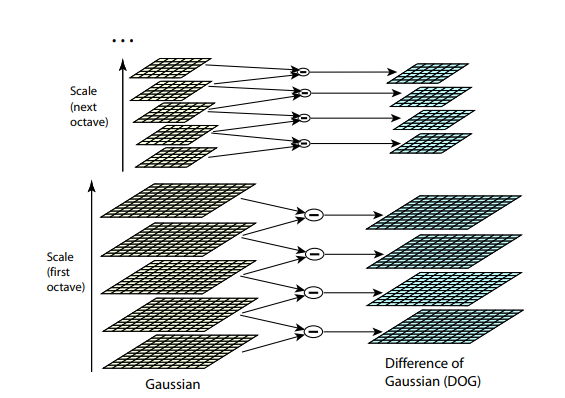
بعد هذا الإجراء ، نحسب الفرق بين المقاييس المجاورة. ستظهر القيم الكبيرة (بالقيمة المطلقة) في هذا الاختلاف في حالة توقف ظهور بعض التفاصيل الصغيرة في المستوى التالي من المقياس ، أو ، على العكس ، يبدأ المستوى التالي من المقياس في التقاط جزء لم يكن مرئيًا في السابق. هذه التقنية تسمى DoG ، اختلاف Gaussian. يمكننا أن نفترض أن الأهمية الكبرى في هذا الاختلاف هي بالفعل إشارة إلى وجود شيء مثير للاهتمام في هذا المكان على الصورة. لكننا مهتمون بالمقياس الذي ستكون فيه هذه النقطة الرئيسية معبرة أكثر. للقيام بذلك ، سننظر في نقطة أساسية ليس فقط كنقطة تختلف عن محيطها ، ولكن أيضًا تختلف بشدة بين مقاييس الصور المختلفة. بمعنى آخر ، سنختار نقطة رئيسية ليس فقط في الفضاءين X و Y ، ولكن في الفضاء $$$(X ، Y ، مقياس)$ . في SIFT ، يتم ذلك عن طريق العثور على نقاط في DoG (Difference of Gaussians) ، والتي هي قمم محلية أو منخفضة في $$$3x3x3$ مكعب من الفضاء $$$(X ، Y ، مقياس)$ من حولها:

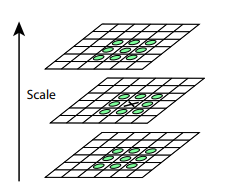
خوارزميات للعثور على النقاط الرئيسية وبناء واصفات SIFT و SURF هي براءة اختراع. وهذا هو ، لاستخدامها التجاري من الضروري الحصول على ترخيص. هذا هو السبب في أنها غير متوفرة من حزمة opencv الرئيسية ، ولكن فقط من حزمة opencv_contrib منفصلة. ومع ذلك ، فإن أبحاثنا حتى الآن أكاديمية بحتة في طبيعتها ، وبالتالي ، لا شيء يمنعنا من المشاركة في SIFT بالمقارنة.

واصفات

دعونا نحاول تطبيق نوع من الكاشف (على سبيل المثال ، هاريس) على القالب والصورة.

بعد العثور على النقاط الرئيسية في الصورة والقالب ، تحتاج إلى المقارنة بينها بطريقة أو بأخرى. واسمحوا لي أن أذكرك أننا لم نستخلص حتى الآن سوى مواقف النقاط الرئيسية. ماذا تعني هذه النقطة (على سبيل المثال ، في أي اتجاه يتم توجيه الزاوية الموجودة) ، لم نحدد بعد. ويمكن أن يساعد هذا الوصف عند مقارنة نقاط الصورة وأنماطها مع بعضها البعض. يمكن تحويل بعض نقاط القالب في الصورة عن طريق التشويهات ، التي تغطيها كائنات أخرى ، وبالتالي فإن الاعتماد فقط على موضع النقاط بالنسبة لبعضها البعض يبدو غير موثوق به. لذلك ، فلنأخذ جوارها لكل نقطة رئيسية من أجل بناء وصف معين (واصف) ، والذي يسمح لنا بعد ذلك بأخذ بضع نقاط (نقطة واحدة من القالب ، واحدة من الصورة) ، ومقارنة التشابه بينهما.

موجز

(.. 0 1), , XOR , . ? , N . , i- , , — i- 1. N. - (, — ), : , “”. , ( ). BRIEF .

. . , GII .

, , (.. , , ). OpenCV .

SIFT

SIFT , . SIFT 1616 , 44 . ( , ). 8 (, -, , ..). — 8 , , . . , 8- . 128 ( 4*4 = 16 , 8 ). .

مقارنة

( — , ), - :

— . ?

, . , , . , , , , . ? BRIEF, , , . , BRIEF 1/16 . SIFT — - 1/4 .

SIFT.

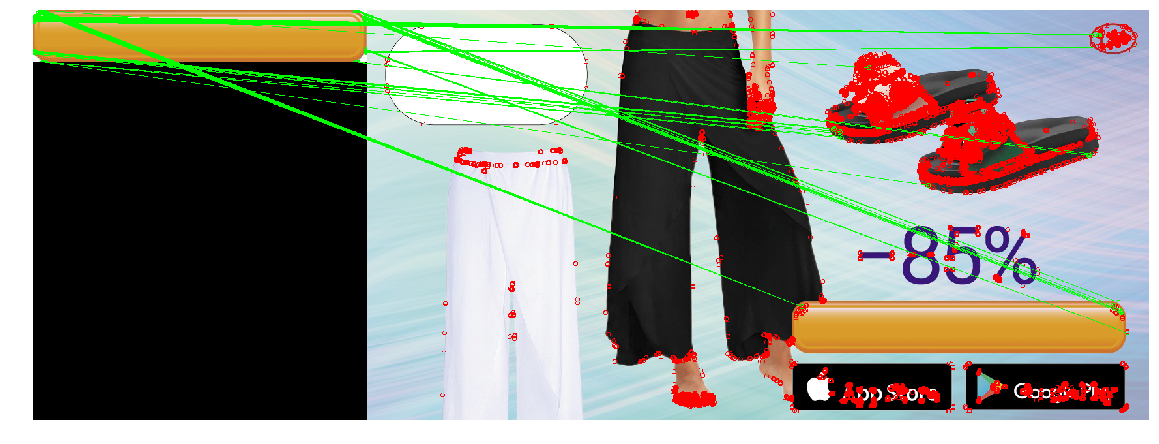
الآن نطبق كل المعرفة المكتسبة لحل مشكلتنا. في حالتنا ، متطلبات كاشف النقاط الرئيسية كافية: لا نحتاج إلى تغيير الثبات ، وكذلك الأداء العالي للغاية. قارن بين الكاشفات الثلاثة.

هاريس كاشف الزاوية	FAST	فرزت

عثر SIFT على عدد قليل جدًا من النقاط الرئيسية على الزر. هذا أمر مفهوم - فالزر كائن صغير ومسطور إلى حد ما ، ولا يساعد التكبير / التصغير في العثور على النقاط الرئيسية.

أيضا ، لم يدير أي كاشف الحالة الثالثة. هذا هو قابل للتفسير والمتوقع. عادةً ما يتم استخدام الأساليب المذكورة أعلاه للعثور على كائن من قالب في صورة حيث يمكن إخفاؤه جزئيًا أو تدويره أو تشويهه قليلاً. في حالتنا ، لا نريد العثور على نفس الكائن تمامًا ، بل كائن مشابه تمامًا للقالب (زر) . هذه مهمة مختلفة قليلاً. لذا ، فإن تغيير شكل الزر نفسه (على سبيل المثال ، دائرة نصف قطر الزوايا ، أو سماكة إطار النقاط) يغير النقاط الرئيسية فيها ، واصفاتها. بالإضافة إلى ذلك ، ستكون النقاط الرئيسية موجودة في زاوية الزر. نظرًا للموضع على الحافة ، ستكون النقاط غير مستقرة: يتأثر موقعها وأوصافها بالضبط بما يتم رسمه بجوار الزر.

خاتمة - الطريقة جيدة ، وتفي بشكل صحيح بالمواقف عندما يكون الكائن المطلوب مستديرًا ، أو يتغير حجمه ، أو يكون الكائن مخفيًا جزئيًا (وهو مفيد للعثور على كائنات معقدة ، أو علامة سعر ، على سبيل المثال). ومع ذلك ، إذا كانت هناك نقاط قليلة على الكائن يمكن "اكتشافها" ، أو يتغير شكل الكائن أكثر من اللازم ، فقد لا تتزامن النقاط الأساسية مع تلك الموجودة في القالب والصورة. أيضًا ، يمكن للخلفية التي تحتوي على الكثير من التفاصيل الصغيرة أن تحول "النقاط الرئيسية" أو تغيير واصفاتها.

يمكننا الخروج بمباراة تستخدم إحداثيات النقاط الرئيسية. بدلاً من البحث عن أزواج من النقاط في القالب والصورة ، حيث يتشابه الحي ، يمكنك البحث عن مجموعات النقاط هذه ، وسيكون التشابه بين النقاط الرئيسية في القالب والصورة متشابهاً. في الحالة العامة ، هذه مهمة معقدة إلى حد ما (من الناحية الحسابية ومن وجهة نظر البرمجة) ، خاصة في المواقف التي يمكن فيها تحويل بعض النقاط أو غيابها. ولكن ، نظرًا لوجود نقاط أساسية - زوايا ، يكفي أن نجد مجموعات ستشكل مستطيلًا تقريبًا بالنسب المرغوبة ، وفي الداخل لن تكون هناك نقاط أساسية. تدريجيا نأتي إلى الطريقة التالية:

كشف كفاف

عادةً ما يكون الزر عبارة عن نوع من الكائنات المستطيلة (أحيانًا مع زوايا دائرية) ، تكون جوانبها موازية لمحور الإحداثيات. ثم دعونا نحاول التمييز بين مناطق اختلاف التباين (الحواف) ، ومن بينها سنجد الوجوه التي تتشابه حدودها مع الخطوط العريضة للكائن الذي نحتاج إليه. وتسمى هذه الطريقة بالكشف الكنتوري.

كشف الحافة

على عكس اكتشاف النقاط الرئيسية ، نحن مهتمون ليس فقط بزوايا النقاط الرئيسية ، ولكن أيضًا بالحواف. ومع ذلك ، فإن الأفكار الأساسية التي يمكن أن نتخذها من هناك. قم بسلاسة الصورة باستخدام مرشح Gaussian ، كما هو الحال في كاشف ركن Harris. ثم نحسب مشتقات الشدة $$$I_x$ و $$$I_y$ . نظرًا لأننا لا نحتاج إلى التمييز بين الزوايا والحواف ، فإننا لسنا بحاجة إلى التفكير في الموتر الهيكلي - يكفي حساب قوة التدرج: $$$I_l = I_x ^ 2 + I_y ^ 2$ (بالمناسبة ، هذا هو جذر $$$Tr (H)$ ، أو من مجموع قطري الموتر الهيكلي). بعد ذلك ، لا نترك سوى وحدات البكسل التي تعد maxima محلية من حيث $$$I_l$ (باستخدام الكبت غير الحد الأقصى المدروس بالفعل) ، لكن كإعدادات محلية ، لن نختار 8 بيكسلات مجاورة ، لكن بيكسلات البيكسلات من هذه الـ 8 ، التي أتوجه إليها ، ومن الجانب الآخر:

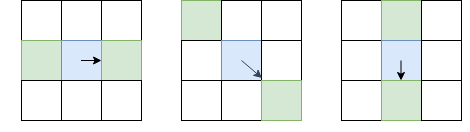
البيكسل المذكور باللون الأزرق ، والسهم هو الاتجاه الأول. البيكسلات الخضراء هي تلك التي ستؤخذ في الاعتبار أثناء الكبت غير الأقصى.

يرجع هذا الاختيار غير العادي لوحدات البكسل للمقارنة ، إلى حقيقة أننا لا نريد أن نجعل الفجوات في الحدود. في الصورة اليسرى ، ينتقل الوجه من أعلى إلى أسفل ، وحيث أن الكبت غير الأقصى لن يقارن الشدة بالبكسل أعلى وأسفل اللون الأزرق ، فإننا نحصل على وجه مستمر.

من الواضح ، عدم كفاية الحد الأقصى واحد لا يكفي ، وتحتاج إلى تطبيق نوع من التصفية لإزالة الحواف مع انخفاض Il. للقيام بذلك ، نطبق تقنية "العتبة المزدوجة": نقوم بإزالة جميع البيكسلات باستخدام Il ، مع قوة تدرج أقل من العتبة المنخفضة ، ونخصص جميع البيكسلات فوق العتبة العالية لتكون "حواف قوية". يطلق على البيكسلات التي تقع فيها قوة التدرج بين المنخفض والارتفاع "الحواف الضعيفة" ، ولا نتركها إلا إذا كانت متصلة "بحواف قوية":

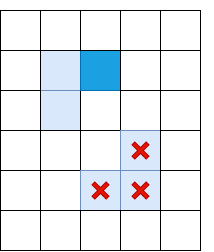
يشير اللون الأزرق الفاتح إلى "ضلوع ضعيفة" ، أزرق غامق - قوي. يتم غربلة الأضلاع في الجزء السفلي ، لأنها غير مرتبطة بأي ضلع قوي.

لقد وصفنا للتو Canny Edge Detector. يستخدم على نطاق واسع حتى يومنا هذا كإجراء بسيط وسريع يتيح لك العثور على ملامح الكائنات.

تتبع الحدود

الإجراء التالي هو تحديد الخطوط بين الخريطة ذات الوجوه التي تم العثور عليها. ابحث عن المكونات ذات الصلة (جزر البيكسلات المجاورة التي اجتازت جميع عمليات الفحص) ، وتحقق من كل منها ، إلى أي مدى يبدو الزر. بعد تطبيق عملية الحد الأقصى غير المسموح به في Canny ، لدينا ضمانات بأن تكون الحواف بسماكة بكسل واحد ، ولكن دعنا نعتمد عليها. لكل بكسل تم تعيينه لوجه ، وبجانبه يوجد بكسل غير وجهي ، نقوم بتعيينه إلى "حد". عند الانتقال من بكسل واحد إلى آخر ، نعود إلى نفس البكسل (ثم وجدنا المسار) ، أو إلى طريق مسدود (ثم يمكنك محاولة العودة إذا كان هناك شوكة في مكان ما على طول الطريق):

خوارزمية تتبع الحدود الكاملة ، مع الأخذ في الاعتبار الحالات المختلفة للحافة (على سبيل المثال ، عندما ينتج كائن ذو وجه سميك محيطين ، داخلي وخارجي) ، موصوف هنا . بعد تطبيق هذه الخوارزمية ، سيكون لدينا مجموعة من المخططات التي يمكن أن تكون أزرارًا.

تصفية المسار

كيف تعرف أن دائرتنا هي زر؟ بالنسبة للمستطيلات والمضلعات ، هناك طريقة ممتازة تعتمد على تبسيط المخطط . يكفي أن "تنهار" الأضلاع تدريجيًا ، إذا كانت على خط مستقيم تقريبًا ، ثم تحسب عدد الأضلاع المتبقية وتحقق من الزوايا بينها. لسوء الحظ ، بالنسبة لحالتنا هذه الطرق ليست مناسبة - المستطيل ذو الزوايا المستديرة. أيضًا ، هناك مطابقة محيطية للأشكال ذات هندسة معقدة - ولكن هذا لا يتعلق بنا أيضًا ، نظرًا لأن لدينا مستطيلًا فقط (يتم تقديم أمثلة ذات مخطط إنساني في المقالة). لذلك ، من الأفضل عمل مرشح بناءً على خصائص الشكل نفسه. نحن نعلم أن:

• الزر كبير بما يكفي (مساحة تزيد عن 100 بكسل)
• الجانبين بالتوازي مع محاور الإحداثيات
• يجب أن تكون نسبة مساحة الشكل إلى مساحة المستطيل المحيط قريبة إلى حد ما من الوحدة. لقد حددنا العتبة على 0.8 ، نظرًا لأن الزر عبارة عن مستطيل ذو جوانب موازية لمحور الإحداثيات ، و 20٪ المفقودة هي الزوايا الدائرية.

بالإضافة إلى ذلك ، من تجربة استخدام أجهزة الكشف عن النقاط الرئيسية ، نتذكر أنه قد تكون هناك مشاكل في المواقف عندما يكون هناك كائن تباين تحت الزر. لذلك ، بعد تطبيق Canny ، نقوم بطمس الحواف لإغلاق الثقوب الصغيرة التي قد تنشأ عن مثل هذه الكائنات.

نحن نطبق النهج الناتج:

عثر تطبيق مرشح Canny (الصورة 2) على الشكل الضروري ، ولكن نظرًا للشكل المعقد للزر والتدرج ، تم العثور على العديد من الأكفة في وقت واحد ، ونتيجة للقمع غير الأقصى لم يتم إغلاق بعضها. تطبيق طمس (3 صور) إصلاح المشكلة.

نهج الاختبار

قم بتشغيل البحث عن ملامح في الصورة الناتجة. تلوين الملامح التي اجتازت الاختبار باللون الأحمر. إذا كان هناك العديد منهم ، فعلينا اختيار الخيار الأكثر نجاحًا بينهم. نختار الخطوط العريضة لأكبر مساحة ونرسمها باللون الأخضر.

| | | |

العثور على تصميم الناتجة أزرار على الصور الاختبار. أظهر التشغيل على جميع الشعارات أنه في بعض الأحيان (حالة واحدة من 20 ~) ، بدلاً من زر ، فإنه يختار مربعات مستطيلة من iOS Appstore و Google Apps ، أو كائنات مستطيلة أخرى (حالات الهاتف). لذلك ، بإضافة القدرة على الإشارة يدويًا إلى الموضع في هذه الحالة النادرة من التحديد الخاطئ ، قمنا بتنفيذ هذا الخيار في أداة التعريب.

استنتاج

لتلخيص. لا تزال السيرة الذاتية "الكلاسيكية" بدون التعلم العميق تعمل ، وبناءً عليه يمكنك حل المشكلات. فهي متواضعة ولا تتطلب قدرًا كبيرًا من البيانات ذات العلامات والأجهزة القوية ، كما أنها أسهل في التصحيح. ومع ذلك ، فإنهم يقدمون افتراضات إضافية ، وبالتالي ، لا يمكن حل كل مشكلة بشكل فعال بمساعدتهم.

• تُعد " مطابقة القوالب " أسهل طريقة ، استنادًا إلى العثور على مكان في الصورة يشبه (في بعض المقاييس البسيطة) القالب. فعال مع بكسل مطابقة بكسل. يمكن جعله مقاومًا للانحناءات والتغيرات الطفيفة في الحجم ، لكن مع التغييرات الكبيرة قد لا يعمل بشكل صحيح.
• اكتشاف / مطابقة Keypoint - ابحث عن النقاط الرئيسية ، وقم بمطابقة نقاط الصورة والقالب. الكاشفات تقاوم الدوران والتكبير (حسب الكاشف والوصف المحدد) ومطابقة - للتداخل الجزئي. ولكن هذه الطريقة لا تعمل بشكل جيد إلا إذا كانت هناك "نقاط أساسية" كافية في الكائن ، وكانت لغات القالب ونقاط الصورة تتطابق جيدًا (أي نفس الكائن في القالب والصورة).
• اكتشاف المحيط - العثور على محيط الكائنات ، والعثور على محيط مماثل لكفاف الكائن المطلوب. يأخذ هذا الحل في الاعتبار فقط شكل الكائن ، ويتجاهل محتوياته ولونه (والذي يمكن أن يكون زائد وناقص).
  قد يلاحظ القارئ ذو المعرفة أن مشكلتنا يمكن حلها بمساعدة أساليب رؤية الكمبيوتر الحديثة المدربة. على سبيل المثال ، تقوم شبكة YOLO بإرجاع المربع المحيط بالكائن المرغوب - وهذا هو ما يهمنا. نعم ، لقد نجحنا في اختبار الحل وإطلاقه استنادًا إلى التعلم العميق - ولكن كتكرار ثانٍ (بالفعل بعد إطلاق أداة التعريب وبدأ العمل). هذه الحلول أكثر مقاومة للتغييرات في معلمات الأزرار ولديها العديد من الخصائص الإيجابية: على سبيل المثال ، بدلاً من التقاط العتبات والمعلمات بيديك ، يمكنك ببساطة إضافة أمثلة للشعارات التي أخطأت الشبكة (التعلم النشط) في مجموعة التدريب عليها. باستخدام التعلم العميق لمهمتنا لديه مشاكله ونقاط مثيرة للاهتمام. على سبيل المثال ، تتطلب العديد من أساليب رؤية الكمبيوتر الحديثة عددًا كبيرًا من الصور التي تم ترميزها ، ولكن لم يكن لدينا علامات (كما في العديد من الحالات الحقيقية) ، ولا يتجاوز العدد الإجمالي للرايات المختلفة عدة آلاف. لذلك ، قررنا وضع عدد صغير من الصور بأنفسنا ، وكتابة مولد سيخلق لافتات أخرى مماثلة على أساسها. في هذا الاتجاه هناك العديد من الحيل المثيرة للاهتمام . هناك العديد من المزالق الأخرى ، ومهمة تحديد موضع كائن رؤية الكمبيوتر واسعة ، ولديها العديد من الحلول. لذلك ، تقرر الحد من مجال رؤية المقال ، ولم يتم النظر في القرارات القائمة على التعلم العميق.

يمكن العثور على الكود الذي يحتوي على دفاتر الملاحظات التي تنفذ الطرق الموضحة ورسم صور المقالة في المستودع ).