المتاهات: التصنيف والجيل والبحث عن الحلول

يعرض هذا المنشور الكلاسيكي تفاصيل أكثر الطرق شيوعًا لإنشاء متاهات وتصفحها. تنقسم المقالة إلى أربعة أجزاء: التصنيف وخوارزميات التوليد وخوارزميات حل المتاهات وغيرها من العمليات باستخدام المتاهات.

تصنيف المتاهة

يمكن تقسيم المتاهات ككل (وبالتالي الخوارزميات الخاصة بإنشائها) إلى سبعة تصنيفات مختلفة: البعد ، فرط البعد ، الطوبولوجيا ، التغطية بالفسيفساء ، التوجيه ، الملمس والأولوية. يمكن للمتاهة استخدام عنصر واحد من كل فئة في أي مجموعة.
البعد: تحدد فئة البعد أساسًا عدد الأبعاد في الفضاء التي تملأها المتاهة. الأنواع التالية متوفرة:

• 
  
  ثنائي الأبعاد : يكون لمعظم المتاهات ، الورقية والحقيقية ، هذا البعد ، أي أنه يمكننا دائمًا عرض مخطط المتاهة على ورقة والتحرك معها دون عبور أي ممرات أخرى من المتاهة.
• ثلاثي الأبعاد : المتاهة ثلاثية الأبعاد لها عدة مستويات ؛ في ذلك (على الأقل في الإصدار المتعامد) ، يمكن للممرات ، بالإضافة إلى الاتجاهات الأربعة الأساسية ، النزول والارتفاع. غالبًا ما يتم عرض متاهة ثلاثية الأبعاد كمجموعة من مستويات ثنائية الأبعاد مع سلالم صعودًا وهبوطًا.
• 
  
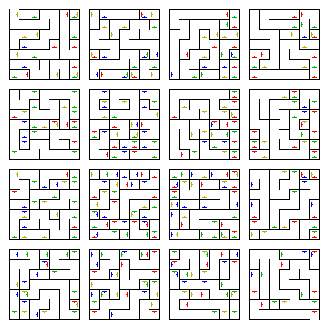
  أبعاد أعلى : يمكنك إنشاء متاهات ثلاثية الأبعاد وحتى أكثر متاهات متعددة الأبعاد. في بعض الأحيان يتم تصويرها على أنها متاهات ثلاثية الأبعاد مع "بوابات" تؤدي إلى البعد الرابع ، على سبيل المثال ، بوابات إلى "الماضي" و "المستقبل".
• 
  
  Interweaving : المتاهات ذات التداخل - هي متاهات ثنائية الأبعاد (أو بالأحرى 2.5-الأبعاد) ، حيث يمكن أن تتداخل الممرات مع بعضها البعض. عند العرض ، يكون من الواضح تمامًا مكان النهايات وكيف تكون إحدى الممرات فوق الأخرى. المتاهات من العالم الحقيقي ، حيث توجد جسور تربط جزءًا من المتاهة بآخر ، متداخلة جزئيًا.

Hyperdimension: التصنيف وفقًا لارتفاع hyperdimension يتوافق مع بُعد كائن يتحرك عبر متاهة ، وليس المتاهة نفسها. الأنواع التالية متوفرة:

• 
  
  غير متشعبات : جميع المتاهات تقريبًا ، حتى تلك المتخلفة في أبعاد عالية أو مع قواعد خاصة ، عادة ما تكون غير متداخلة. في نفوسهم نعمل مع نقطة أو كائن صغير ، على سبيل المثال ، كرة أو اللاعب نفسه ، الذي ينتقل من نقطة إلى نقطة ، والطريق المعبّد يشكل خطًا. في كل نقطة ، هناك عدد من الخيارات يمكن حسابه بسهولة.
• Hyperlabyrinths: hyperlabyrinths هي متاهات حيث الكائن الذي يتم حله ليس مجرد نقطة. يتكون مستوى التشعب القياسي (أو التشعب الأول من الدرجة الأولى) من خط يشكل سطحًا عند التحرك على طول مسار. لا يمكن أن يوجد Hyperlabyrinth إلا في ثلاثي الأبعاد أو في وسيط ذي بعد أكبر ، وغالبًا ما يكون مدخل Hyperlabyrinth نقطة بل خط. تختلف Hyperlabyrinth اختلافًا جذريًا ، لأنه من الضروري أن تؤخذ في الاعتبار والعمل مع عدة أجزاء على طول الخط في وقت واحد ، وفي أي وقت معطى يوجد عدد لا حصر له من الحالات والخيارات لما يمكن القيام به مع الخط. خط الحل لا حصر له ، أو أن نقاط النهاية الخاصة به تقع خارج نطاق التشعب لتجنب ضغط الخط إلى حد ما ، لأنه في هذه الحالة يمكن اعتباره غير متشعب.
• Hyper-Hyperlabyrinth: Hyper-Hyperlabyrinth: Hyper-Hyperlabyrinth: يمكن أن تكون Hyperlabyrinths ذات أبعاد عالية بشكل تعسفي. يزيد Hyper-Hyperlabyrinth (أو hyperlabyrinth من الترتيب الثاني) مرة أخرى البعد الكائن الذي يتم حلها. هنا ، الكائن المراد حله هو الطائرة ، والتي عندما تتحرك على طول المسار ، تشكل شخصية ثلاثية الأبعاد. Hyper-Hyperlabyrinth لا يمكن أن يوجد إلا في بيئة ثنائية الأبعاد أو أعلى الأبعاد.

الطوبولوجيا: تصف فئة الطوبولوجيا هندسة مساحة المتاهة التي توجد فيها ككل. الأنواع التالية متوفرة:

• 
  
  عادي : هذا هو المتاهة القياسية في المساحة الإقليدية.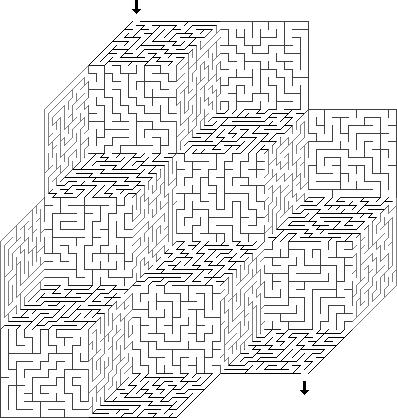
• 
  
  المستوى : يصف مصطلح "planair" أي متاهة ذات طوبولوجيا غير عادية. عادة ما يعني هذا أن حواف المتاهة مرتبطة بطريقة مثيرة للاهتمام. الأمثلة على ذلك: المتاهات على سطح المكعب ، والمتاهات على سطح شريط Mobius والمتاهات المكافئة لتلك الموجودة في torus حيث يتم توصيل الجانبين الأيسر والأيمن ، العلوي والسفلي في أزواج.

التغطية بالفسيفساء: تصنيف للهندسة من الخلايا الفردية التي تشكل المتاهة. الأنواع الحالية:

• 
  
  متعامد : هذا هو شبكة مستطيلة قياسية فيها الخلايا التي تتقاطع الممرات في الزوايا اليمنى. في سياق التغطية بالفسيفساء ، يمكن أيضا أن تسمى متاهات جاما.
• 
  
  دلتا : تتكون متاهات دلتا من مثلثات متصلة ، ويمكن أن تحتوي كل خلية على ما يصل إلى ثلاثة مقاطع متصلة بها.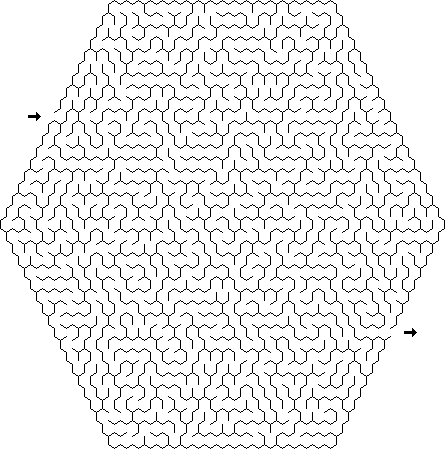
• 
  
  Sigma : تتكون متاهات Sigma من مسدسات متصلة ؛ يمكن أن تحتوي كل خلية على ستة تصاريح.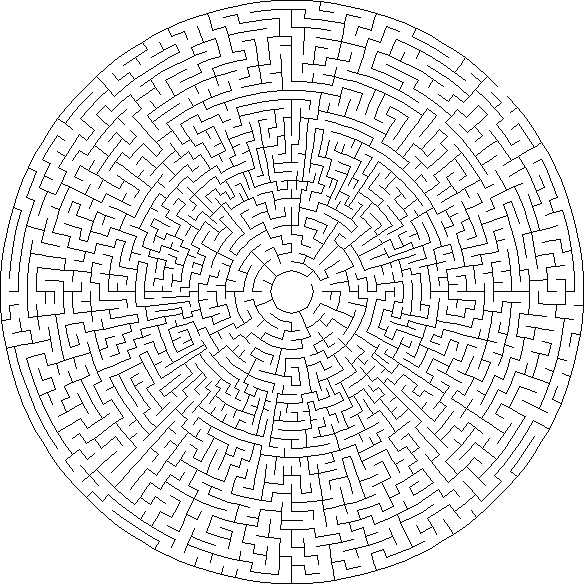
• 
  
  ثيتا : تتكون متاهات ثيتا من دوائر متحدة المركز من الممرات حيث تكون البداية أو النهاية في المنتصف والأخرى على الحافة الخارجية. عادة ما يكون للخلايا أربعة مسارات اتصال محتملة ، ولكن قد يكون هناك المزيد بسبب زيادة عدد الخلايا في الحلقات الخارجية للممرات.
• 
  
  Epsilon : تتكون متاهات Epsilon من ثماني أو مربعات متصلة ، ويمكن أن يكون لكل خلية فيها ما يصل إلى ثمانية أو أربعة تمريرات.
• 
  
  زيتا : تقع متاهة زيتا على شبكة مستطيلة ، فقط بالإضافة إلى الممرات الأفقية والعمودية ، يسمح للممرات القطرية بزاوية 45 درجة.
• 
  
  أوميغا : يشير مصطلح أوميغا إلى أي متاهة تقريبًا مع تغطية بالفسيفساء غير متعامدة. تعتبر متاهات دلتا وسيغما وثيتا وإبسيلون من هذا النوع ، مثل العديد من المخططات الأخرى التي يمكنك التفكير فيها ، على سبيل المثال ، متاهة تتكون من أزواج من مثلثات قائمة الزاوية.
• 
  
  الكراك : متاهة الكراك عبارة عن متاهة غير متبلورة بدون غطاء أرضي ثابت ، حيث توجد الجدران والممرات في زوايا عشوائية.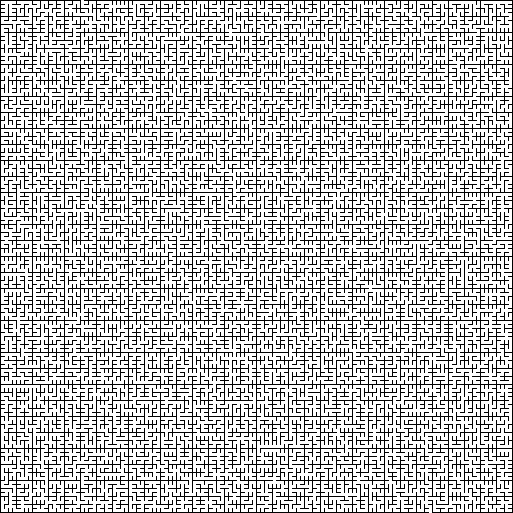
• 
  
  كسورية : متاهة كسورية هي متاهة تتكون من متاهات أصغر. المتاهة الكسورية من الخلايا المتداخلة هي متاهة في كل خلية توضع فيها متاهات أخرى ، ويمكن تكرار هذه العملية عدة مرات. المتاهة الفركتل العودية بلا حدود هي الفراكتل الحقيقي الذي تتكرر فيه محتويات المتاهة ، مما يخلق متاهة كبيرة بشكل لا نهائي.

التوجيه: التصنيف من خلال التوجيه ربما يكون الجانب الأكثر إثارة للاهتمام في توليد متاهات. من يرتبط بأنواع التمريرات داخل الهندسة المحددة في الفئات الموضحة أعلاه.

• 
  
  مثالي : "مثالي" عبارة عن متاهة بدون حلقات أو دوائر مغلقة وبدون مناطق يتعذر الوصول إليها. ويسمى أيضا متاهة متصلة ببساطة. من كل نقطة يوجد مسار واحد بالضبط لأي نقطة أخرى. المتاهة لديها حل واحد فقط. من وجهة نظر البرمجة ، يمكن وصف مثل هذه المتاهة بأنها شجرة أو مجموعة متصلة من الخلايا أو الرؤوس.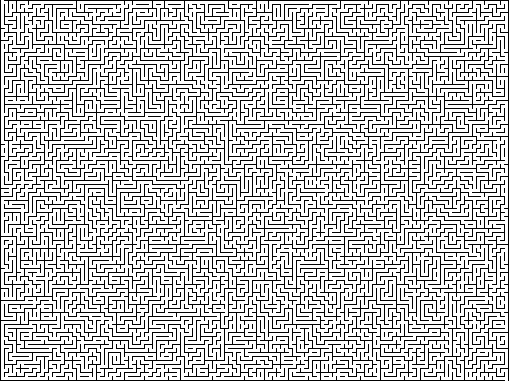
• 
  
  مضفر : مضفر يعني أنه لا توجد مسدود في المتاهة. ويطلق عليه أيضا متاهة متاهة تتضاعف بحتة متصلة. في مثل هذا المتاهة ، يتم استخدام الممرات التي يتم إغلاقها والعودة إلى بعضها البعض (وبالتالي اسم "الخوص") ، فإنها تجعلهم يقضون المزيد من الوقت في المشي في دوائر بدلاً من الدخول في طريق مسدود. يمكن أن تكون المتاهة المنسوجة عالية الجودة أكثر تعقيدًا من المتاهة المثالية من نفس الحجم.
• 
  
  المسار الأحادي (Unicursal) : المسار الفردي يعني متاهة بدون شوكات. تحتوي المتاهة أحادية الاتجاه على مقطع متعرج طويل يغير الاتجاه عبر المتاهة. ليس الأمر معقدًا للغاية ، فقط إذا لم تتراجع بطريق الخطأ إلى منتصف الطريق ولا تعود إلى البداية.
• 
  
  متفرق: متاهة متفرق لا يجعل يمر عبر كل خلية ، وهذا هو ، لم يتم إنشاء بعضها. هذا يعني وجود مناطق لا يمكن الوصول إليها ، وهذا ، إلى حد ما ، هو عكس متاهة الخوص. يمكن تطبيق مفهوم مماثل عند إضافة الجدران ، بحيث يمكنك الحصول على متاهة غير متساوية مع ممرات وغرف واسعة.
• الغصن جزئيًا: الغصن الجزئي المتاهة عبارة عن متاهة مختلطة تشتمل على حلقات ونهايات مسدودة. يمكن استخدام كلمة "wicker" للتقييم الكمي ، أي "متاهة ذات نسج قوي" هي متاهة بها العديد من الحلقات أو الجدران التي تمت إزالتها ، وهناك عدد قليل منها في "متاهة ذات نسج ضعيف".

الملمس: يصف تصنيف الملمس نمط التمرير باستخدام التوجيه والهندسة المختلفة. الملمس ليس مجرد معلمات يمكن تشغيلها أو إيقاف تشغيلها. فيما يلي بعض الأمثلة للمتغيرات:

• 
  
  انحياز : في متاهة مع الممرات النازحة ، تميل الممرات المستقيمة إلى الذهاب في اتجاه واحد أكثر من غيرها. على سبيل المثال ، في متاهة ذات إزاحة أفقية عالية ، سيكون لدينا ممرات طويلة من اليسار إلى اليمين ، وممرات قصيرة فقط من أعلى إلى أسفل تربطها. هذه المتاهة عادة ما تكون أكثر صعوبة في تمرير "عبر الألياف".
• 
  
  Overflight : يحدد قياس Overflight المدة التي تستغرقها الممرات قبل ظهور المنعطفات القسرية. في متاهة ذات فترة منخفضة ، لن يكون هناك ممرات مستقيمة أطول من ثلاث أو أربع خلايا ، وسوف تبدو عشوائية للغاية. في المتاهة ذات الامتداد العالي ، ستحتوي المتاهة على نسبة كبيرة من التمريرات الطويلة ، مما سيجعلها تبدو وكأنها رقاقة دقيقة.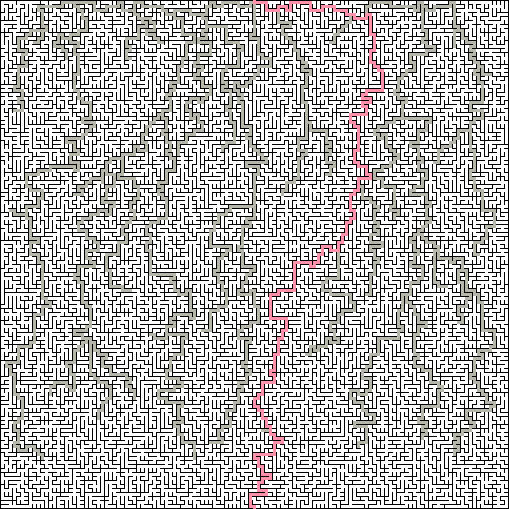
• 
  
  النخبوية: يحدد مؤشر " النخبوية " في المتاهة طول الحل بالنسبة لحجم المتاهة. عادة ما يكون لدى المتاهات النخبة حل قصير ومباشر ، بينما في المتاهات غير النخبة ، ينتقل المحلول إلى جزء كبير من مساحة المتاهة. يمكن أن تكون متاهة النخبة عالية الجودة أكثر تعقيدًا من متاهة غير النخبة.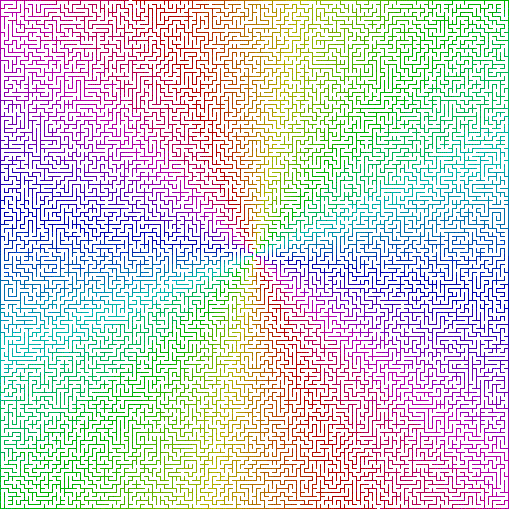
• 
  
  التماثل : متاهة متماثلة لها ممرات متناظرة ، على سبيل المثال ، في تناظر الدوران بالنسبة للمركز ، أو تنعكس على طول المحاور الأفقية أو الرأسية. يمكن أن تكون المتاهة متماثلة جزئيًا أو كليًا ، ويمكن أن تكرر النموذج أي عدد من المرات.
• 
  
  التجانس: تقوم الخوارزمية المتجانسة بإنشاء كل المتاهات المحتملة باحتمال متساوٍ. يمكن تسمية المتاهة بوجود نسيج متجانس إذا كان يشبه متاهة نموذجية تم إنشاؤها بواسطة خوارزمية متجانسة. يمكن للخوارزمية غير المتجانسة من الناحية النظرية أيضًا أن تولد جميع المتاهات المحتملة في أي مكان ، ولكن ليس باحتمالية متساوية. يمكن أن يزيد عدم التجانس أكثر - قد تكون هناك متاهات لن تولدها الخوارزمية أبدًا.
• تدفق النهر: تعني خاصية "التدفق" أنه عند إنشاء متاهة ، ستبحث الخوارزمية وتنظف الخلايا المجاورة (أو الجدران) إلى الخلية الحالية ، أي أنها ستتدفق (ومن هنا جاءت عبارة "السيولة") في الأجزاء التي لا تزال غير متشكلة من المتاهة ، مثل الماء. في المتاهة المثالية ذات معدل التدفق المنخفض ، عادة ما يكون هناك العديد من النهايات المسدودة ، وفي المتاهة "الأكثر مرونة" سيكون هناك عدد أقل من النهايات المسدودة ، لكنها ستكون أطول.

الأولوية: يوضح هذا التصنيف أن عمليات إنشاء متاهات يمكن تقسيمها إلى نوعين رئيسيين: إضافة الجدران وممرات نحت. عادةً ، عند إنشاء هذا ، يعود الاختلاف في الخوارزميات فقط ، وليس إلى الاختلافات الملحوظة في المتاهات ، ولكن لا يزال من المفيد مراعاة ذلك. غالبًا ما يتم إنشاء نفس المتاهة بطريقتين:

• إضافة الجدران: تبدأ الخوارزميات التي تكون لها أولوية بالنسبة لأولوية بمساحة خالية (أو حدود خارجية) ، مع إضافة الجدران في العملية. في العالم الواقعي ، تضيف المتاهات الحقيقية المكونة من سياج أو سقوف أو جدران خشبية بالتأكيد الجدران.
• ممرات القطع: تبدأ الخوارزميات ذات الأولوية بالنسبة للممرات بكتلة صلبة وتقطع الممرات فيها. في العالم الواقعي ، مثل المتاهات هي أنفاق الألغام أو المتاهات داخل الأنابيب.
• 
  
  قالب: بالطبع ، يمكن للمتاهات قطع الممرات في وقت واحد وإضافة الجدران ؛ بعض خوارزميات الكمبيوتر تفعل ذلك. قالب المتاهة هو صورة رسومية ليست متاهة ، والتي تتحول في أقل عدد من الخطوات إلى متاهة حقيقية ، ولكنها لا تزال تحتفظ بنسيج قالب الرسوم الأصلي. من السهل تنفيذ أنماط المتاهة المعقدة ، مثل اللوالب المتقاطعة ، كأنماط في الكمبيوتر ، بدلاً من محاولة إنشاء المتاهة الصحيحة مع الحفاظ على نمطها.

أخرى: ما سبق ليس بأي حال قائمة شاملة لجميع الفئات أو العناصر الممكنة داخل كل فصل. هذه فقط أنواع المتاهات التي خلقتها بنفسي. لاحظ أن كل نوع من المتاهات تقريبًا ، بما في ذلك المتاهات ذات القواعد الخاصة ، يمكن التعبير عنه كرسم بياني موجه ، حيث سيكون هناك عدد محدد من الحالات وعدد محدد من الاختيارات في كل ولاية ، وهذا ما يسمى معادلة المتاهات . فيما يلي بعض التصنيفات وأنواع المتاهات الأخرى:

• 
  
  الاتجاه : في بعض المقاطع ، يمكنك فقط التحرك في اتجاه واحد. من وجهة نظر البرمجة ، سيتم وصف مثل هذا المتاهة بواسطة رسم بياني موجه ، على عكس الرسم البياني غير الموجه الذي يصف جميع الأنواع الأخرى.
• 
  
  تجزئة : يمكن أن يكون المتاهة أجزاء مختلفة المقابلة لفئات مختلفة.
• 
  
  المتاهات ذات الطول اللانهائي: يمكننا إنشاء متاهة طويلة بلا حدود (عدد محدود من الأعمدة وأي عدد من الصفوف) ، ولكن في نفس الوقت ، يتم تخزين جزء واحد فقط من المتاهة في الذاكرة ، "التمرير" من طرف إلى آخر وتدمير الأسطر السابقة عند إنشاء التالي. أحد الأمثلة على ذلك هو نسخة معدلة من خوارزمية Hunt و Kill. يمكن للمرء أن يتخيل متاهة لا نهاية لها على شكل فيلم طويل يتكون من إطارات فردية. يتم تخزين إطارين متتاليين فقط في الذاكرة في كل مرة. لنقم بتشغيل خوارزمية Hunt و Kill ، على الرغم من أنه يخلق تحيزًا عرضة للإطار العلوي ، بحيث ينتهي أولاً. بعد الانتهاء ، لم تعد هناك حاجة للإطار ، يمكنك طباعته أو القيام بشيء آخر به. مهما كان الأمر ، تجاهلها ، وجعل الإطار السفلي الذي تم إنشاؤه جزئيًا إطارًا علويًا جديدًا ومسح الإطار السفلي الجديد. كرر العملية حتى نقرر التوقف ، ثم انتظر حتى تكمل Hunt And Kill كلا الإطارين. القيد الوحيد هو أن المتاهة لن يكون لها طريق يتفرع في اتجاه المدخل بطول أكثر من إطارين. أسهل طريقة لإنشاء متاهة لا نهاية لها هي خوارزمية Eller أو خوارزمية Sidewinder ، لأنها تقوم بالفعل بإنشاء متاهات سطر واحد في وقت واحد ، لذلك يمكنك السماح لهم بإضافة خطوط إلى المتاهة بلا نهاية.
• 
  
  متاهات افتراضية افتراضية : المتاهة افتراضية هي متاهة لا يتم تخزين المتاهة بأكملها في الذاكرة في نفس الوقت. على سبيل المثال ، لا يمكنه تخزين سوى جزء من ممرات 100 × 100 بالقرب من موقعك في محاكاة حيث تجول عبر متاهة كبيرة. يمكن استخدام امتداد المتاهات الكسورية المتداخلة لإنشاء متاهات افتراضية ضخمة ، على سبيل المثال ، مليار لكل مليار تمريرة. إذا بنينا نسخة حقيقية من المتاهة من مليار مليار تمر (بمسافة ستة أقدام بين الممرات) ، فستملأ سطح الأرض أكثر من 6000 مرة! النظر في متاهة من 10 ⁹ إلى ^{9 9} يمر ، أو متاهة المغلقة مع 9 مستويات فقط. إذا كنا نريد على الأقل جزءًا 100 × 100 من حولنا ، فهذا يكفينا لإنشاء متاهة فرعية على الأقل 100 × 100 وسبعة متاهات 10x10 متضمنة فيها من أجل معرفة مكان وجود الجدران في الجزء 100 × 100 تمامًا. (في الواقع ، من الأفضل أن يكون لديك أربعة أجزاء متجاورة بحجم 100 × 100 ، وتشكل مربعًا إذا كنت بالقرب من حافة الجزء أو الركن منه ، ولكن نفس المفهوم ينطبق هنا.) لضمان ثبات المتاهة عند تحريكها ، لدينا صيغة ، تحديد رقم البذور عشوائي لكل إحداثي في ​​كل مستوى التعشيش. تشبه متاهات الفركتل الافتراضية الفركتلات الماندلبروت ، التي توجد صورها فعليًا ، ونحن بحاجة إلى زيارة إحداثيات معينة بتكبير مرتفع إلى حد ما. بحيث يبدو.

خوارزميات المتاهة

فيما يلي قائمة بالخوارزميات المعممة لإنشاء فئات مختلفة من المتاهات الموضحة أعلاه:

• 
  
  مثالي : لإنشاء متاهة مثالية قياسية ، من الضروري عادة "نموها" ، مع ضمان عدم وجود حلقات ومناطق معزولة. نبدأ من الجدار الخارجي ونضيف بشكل عشوائي جزءًا من الجدار يلامسه. نستمر في إضافة شرائح الجدار بشكل عشوائي إلى المتاهة ، ولكن تأكد من أن كل شريحة جديدة تلامس من أحد طرفي الجدار الحالي ، وأن الطرف الآخر في الجزء الذي لم يتم إنشاؤه بعد من المتاهة. إذا قمت بإضافة قطعة حائط ، يتم فصل طرفيها عن بقية المتاهة ، فسيؤدي ذلك إلى إنشاء جدار غير متصل مع حلقة حوله ، وإذا قمت بإضافة قطعة ، كلا الطرفين تلمس المتاهة ، فسيؤدي ذلك إلى إنشاء منطقة يتعذر الوصول إليها. هذه طريقة لإضافة الجدران. من شبه المماثل قطع الممرات ، حيث يتم قطع أجزاء من الممرات بحيث تلامس طرف واحد فقط الممر الحالي.
• 
  
  : , , . : (1) , (2) , , -«», (3) , , , (4) , , (3) , , .
• 
  
  : — , , , , . U- , , , , . . , : , , , . , . , .
• 
  
  : , . , , . - , , , , .
• 3D : , , , . - .
• 
  
  : , , . ( ): , , , . , . , ; , . , , .
• 
  
  Crack : Crack- , , . , , , «» . , , . , - . , , ; . , .
• 
  
  : «» , , . , - : (1) , . (2) , , , , , (.. ). (3) , , . , .
• 
  
  : — 3D-, -, , . 3D- , , . , , . , . , ( ), , , .
• 
  
  Planair : Planair- , . — . , .
• 
  
  : , , , -, , , , . , . , , , , , .

هناك العديد من الطرق لإنشاء متاهات مثالية ، ولكل منها خصائصه الخاصة. أدناه قائمة خوارزميات محددة. يصف كل منهم إنشاء متاهة من خلال الاستغناء عن الممرات ، ومع ذلك ، ما لم يُذكر خلاف ذلك ، يمكن أيضًا تنفيذ كل منها بإضافة جدران:

• 
  
  تراجع متكرر : - recursive backtracker, , . , , . , , . , . , . , , , . , . Recursive backtracking , , , .
• 
  
  : , . , «» , , . , , ( ). , . , , . , - , , . , , . , . , - (union-find algorithm): , . . , - .
• 
  
  خوارزمية Prim (حقيقية) : تقوم هذه الخوارزمية بإنشاء شجرة تمتد على الحد الأدنى عن طريق معالجة أوزان الحافة العشوائية الفريدة. يتناسب حجم الذاكرة المطلوبة مع حجم المتاهة. نبدأ من أي قمة (المتاهة النهائية ستكون هي نفسها ، بغض النظر عن القمة التي نبدأها). نختار حافة المقطع مع أقل وزن يربط المتاهة بنقطة غير موجودة فيها بالفعل ، ثم نعلقها على المتاهة. يتم الانتهاء من المتاهة عندما لم تعد الحواف موضوع اليسار. لتحديد الحافة التالية بكفاءة ، تحتاج إلى قائمة انتظار أولوية (يتم تنفيذها عادةً باستخدام كومة) لتخزين كل حواف الحد. ومع ذلك ، فإن هذه الخوارزمية بطيئة إلى حد ما لأن الأمر يستغرق وقتًا في السجل (n) لتحديد العناصر من الكومة. لذلك ، من الأفضل تفضيل خوارزمية Kraskal ، التي تنشئ أيضًا شجرة تمد أدنى ، لأنها أسرع وتخلق متاهات ذات بنية مماثلة. في الواقع ، مع نفس البذور العشوائية ، يمكن لخوارزميات بريما وكراسكال إنشاء نفس المتاهات.
• 
  
  خوارزمية Prim (المبسطة) : تقوم خوارزمية Prim هذا بخلق شجرة تمد دنيا. يتم تبسيطها بحيث تكون جميع أوزان الحواف متماثلة. يتطلب سعة ذاكرة تتناسب مع حجم المتاهة. نبدأ من ذروة عشوائية. نختار بشكل عشوائي حافة المقطع الذي يربط المتاهة بنقطة لم تدخلها بعد ، ثم نعلقها على المتاهة. يتم الانتهاء من المتاهة عندما لم تعد الحواف موضوع اليسار. نظرًا لأن الحواف قليلة الوزن وليست مرتبة ، يمكن تخزينها كقائمة بسيطة ، أي أن اختيار العناصر من القائمة سيكون سريعًا جدًا ويستغرق وقتًا ثابتًا. لذلك ، فهي أسرع بكثير من خوارزمية Prim الحقيقية مع أوزان حافة عشوائية. سيكون لملمس المتاهة الذي تم إنشاؤه مؤشر انخفاض العائد وحل أبسط من خوارزمية Prima الحقيقية ، لأنه ينتشر من نقطة البداية بالتساوي ، مثل شراب مسكوب ، ولا يتجاوز شظايا الأضلاع ذات الوزن الأعلى ، والتي تؤخذ في الاعتبار لاحقًا.
• 
  
  خوارزمية Prim (معدلة) : تقوم خوارزمية Prim بهذا بإنشاء شجرة تمتد قليلة ، معدلة بحيث تكون جميع أوزان الحواف متماثلة. ومع ذلك ، يتم تطبيقه بطريقة أنه بدلاً من الحواف فإنه ينظر إلى الخلايا. يتناسب حجم الذاكرة مع حجم المتاهة. في عملية الخلق ، يمكن أن تحتوي كل خلية على ثلاثة أنواع: (1) "داخلي": الخلية جزء من المتاهة ومقطوعة بالفعل ، (2) "حدود": الخلية ليست جزءًا من المتاهة ولم يتم قطعها بعد ، ولكنها تقع بجانب الخلية التي هي بالفعل "داخلية" ، و (3) "خارجية": الخلية ليست بعد جزءًا من المتاهة ، وأي من جيرانها ليس هو أيضًا الخلية "الداخلية". نبدأ باختيار خلية ونجعلها "داخلية" ، وبالنسبة لجميع جيرانها نضع النوع على "الحدود". نختار بشكل عشوائي الخلية "الحدودية" ونقطع مقطعًا من إحدى الخلايا "الداخلية" المجاورة فيه. نغير حالة هذه الخلية "الحدودية" إلى "داخلية" ونغير نوع كل جيرانها من "خارجي" إلى "حد". يتم إكمال المتاهة عندما لا توجد خلايا "حدودية" متبقية (أي ، لا توجد خلايا "خارجية" متبقية ، مما يعني أن كل شخص أصبح "داخليًا"). تقوم هذه الخوارزمية بإنشاء متاهات ذات مؤشر عائد منخفض للغاية ، ولديها العديد من الجمود القصيرة والحل الصريح. يشبه المتاهة الناتجة إلى حد كبير نتيجة طريقة Prim المبسطة ، مع اختلاف بسيط: يتم ملء الفراغات في شجرة الامتداد فقط إذا تم اختيار خلية حدود بشكل عشوائي ، على عكس الاحتمال الثلاثي لملء هذه الخلية من خلال إحدى الخلايا الحدودية المؤدية إليها. بالإضافة إلى ذلك ، الخوارزمية سريعة جدًا ، أسرع من خوارزمية Prim المبسطة ، لأنها لا تحتاج إلى تجميع ومعالجة قائمة الحواف.
• 
  
  خوارزمية Aldous-Broder : الشيء المثير للاهتمام في هذه الخوارزمية هو أنها متجانسة ، أي أنها تخلق مع الاحتمال المتساوي جميع المتاهات الممكنة من حجم معين. بالإضافة إلى ذلك ، لا يتطلب ذاكرة إضافية أو مكدس. نختار نقطة وننتقل بشكل عشوائي إلى خلية مجاورة. إذا وصلنا إلى خلية غير مقطوعة ، فقم بقطع الممر من الخلية السابقة فيه. نواصل الانتقال إلى الخلايا المجاورة حتى نقطع الممرات إلى جميع الخلايا. تقوم هذه الخوارزمية بإنشاء متاهات ذات معدل تدفق منخفض ، أعلى قليلاً فقط من خوارزمية Kraskal. (وهذا يعني أنه بالنسبة لتبادل معين ، يوجد عدد أكبر من المتاهات ذات مؤشر عائد منخفض مقارنة بالمستوى العالي ، لأن المتاهة ذات الاحتمال المتوسط ​​منخفضة على حد سواء.) والشيء السيئ في هذه الخوارزمية هو أنها بطيئة للغاية لأنها لا تقوم بالبحث الفكري عن الأخير الخلايا ، وهذا ، في الواقع ، ليس لديها ضمانات للإنجاز. ومع ذلك ، بسبب بساطته ، يمكنه الانتقال بسرعة عبر العديد من الخلايا ، لذلك يكتمل بشكل أسرع مما تعتقد. في المتوسط ​​، يستغرق إكماله سبع مرات أطول من الخوارزميات القياسية ، على الرغم من أنه في الحالات السيئة قد يستغرق وقتًا أطول إذا تجنب مولد الأرقام العشوائية الخلايا القليلة الأخيرة باستمرار. يمكن تطبيقه كإضافة للجدران ، إذا كان الجدار الحدودي يعتبر قمة واحدة ، على سبيل المثال ، إذا نقلتنا هذه الخطوة إلى الجدار الحدودي ، فإننا ننتقل إلى نقطة عشوائية على طول الحدود ، ثم نستمر في الحركة. في حالة إضافة الجدران ، يعمل بسرعة تقارب مرتين ، لأن النقل عن بعد على طول الجدار الحدودي يسمح بالوصول بشكل أسرع إلى الأجزاء البعيدة من المتاهة.
• 
  
  خوارزمية ويلسون : هذه نسخة محسّنة من خوارزمية ألدوس برودر ، فهي تخلق متاهات بنفس الملمس تمامًا (الخوارزميات متجانسة ، أي يتم إنشاء جميع المتاهات المحتملة باحتمال متساوٍ) ، لكن خوارزمية ويلسون أسرع بكثير. يستغرق ذاكرة تصل إلى حجم المتاهة. نبدأ مع خلية متاهة الأولية المحددة عشوائيا. نختار خلية عشوائية لا تشكل جزءًا من المتاهة ونقوم بالسير بشكل عشوائي حتى نعثر على خلية تنتمي بالفعل إلى المتاهة. بمجرد أن نتعثر على الجزء الذي تم إنشاؤه بالفعل من المتاهة ، نعود إلى الخلية العشوائية المحددة ونقطع المسار بالكامل الذي يتم عن طريق إضافة هذه الخلايا إلى المتاهة. وبشكل أكثر تحديداً ، عندما نعود على طول المسار ، نقطع كل خلية في الاتجاه الذي تم فيه السير العشوائي في آخر مرة تركنا فيها الخلية. هذا يتجنب ظهور الحلقات على طول مسار الإرجاع ، بحيث ينضم مقطع طويل إلى المتاهة. اكتمال المتاهة عندما يتم إرفاق جميع الخلايا به. تواجه الخوارزمية نفس مشاكل السرعة مثل Aldous-Broder ، لأنه قد يستغرق وقتًا طويلاً للعثور على أول مسار عشوائي للخلية الأولية ، ولكن بعد وضع عدة مسارات ، يتم قطع بقية المتاهة بسرعة كبيرة. في المتوسط ​​، يتم تشغيله أسرع بخمس مرات من Aldous-Broder ، وأقل من مرتين أسرع من أفضل الخوارزميات. تجدر الإشارة إلى أنه في حالة إضافة الجدران ، يعمل مرتين بأسرع ، لأن الجدار الحدودي بالكامل هو في البداية جزء من المتاهة ، وبالتالي فإن الجدران الأولى تنضم بشكل أسرع.
• 
  
  مطاردة وقتل الخوارزمية : هذه الخوارزمية مريحة لأنها لا تتطلب ذاكرة إضافية أو مكدس ، وبالتالي فهي مناسبة لإنشاء متاهات ضخمة أو متاهات على أجهزة الكمبيوتر ضعيفة بسبب استحالة نفاد الذاكرة. نظرًا لعدم وجود قواعد تحتاج إلى اتباعها باستمرار ، فمن الأسهل أيضًا تعديل وإنشاء متاهات ذات مواد مختلفة تستخدمها. إنه يشبه تقريبًا مسار تراجع متكرر ، فقط لا توجد خلية لم يتم إنشاؤها بالقرب من الموضع الحالي. ندخل في وضع "الصيد" ونقوم بمسح المتاهة ضوئيًا بشكل منهجي حتى نعثر على خلية غير مكونة بجوار الخلية المقطوعة بالفعل. في هذه المرحلة ، نبدأ مرة أخرى في قطع هذا الموقع الجديد. اكتمال المتاهة عندما يتم فحص جميع الخلايا في وضع "الصيد". تميل هذه الخوارزمية إلى إنشاء متاهات ذات معدل تدفق عالٍ ، ولكن ليس بنفس درجة تراجعي العودية. يمكنك إجبارها على إنشاء متاهات بمعدل تدفق أقل ، وغالبًا ما تدخل في وضع "الصيد". إنه يعمل بشكل أبطأ بسبب الوقت الذي يقضيه في صيد الخلايا الأخيرة ، ولكن ليس أبطأ بكثير من خوارزمية Kraskal. يمكن تنفيذه وفقًا لمبدأ إضافة الجدران ، إذا كنت تنتقل من وقت لآخر بشكل عشوائي لتجنب المشاكل الكامنة في تراجع متكرر.
• 
  
  تزايد الخوارزمية
  tree (خوارزمية شجرة متنامية) : هذه خوارزمية معممة يمكنها أن تنشئ متاهات ذات قوام مختلف. يمكن أن تصل الذاكرة المطلوبة إلى حجم المتاهة. في كل مرة يتم فيها قطع خلية ، نضيفها إلى القائمة. حدد خلية من القائمة وقطع المقطع إلى الخلية التي لم يتم إنشاؤها بجوارها. إذا لم تكن هناك خلايا غير منشورة بالقرب من الخلية الحالية ، فاحذف الخلية الحالية من القائمة. اكتمال المتاهة عندما لا يوجد شيء آخر في القائمة. الشيء المثير للاهتمام حول الخوارزمية هو أنه ، بناءً على كيفية تحديد خلية من القائمة ، يمكنك إنشاء العديد من القوام المختلفة. على سبيل المثال ، إذا قمت دائمًا بتحديد آخر خلية مضافة ، فستتحول هذه الخوارزمية إلى متراجع متكرر. إذا قمت دائمًا بتحديد الخلايا بشكل عشوائي ، فسوف تتصرف بشكل مشابه ، ولكن ليس بطريقة مماثلة لخوارزمية Prim. إذا قمت دائمًا بتحديد أقدم الخلايا التي تمت إضافتها إلى القائمة ، فسنقوم بإنشاء متاهة تحتوي على أقل مؤشر إنتاج ممكن ، حتى أقل من خوارزمية Prim. إذا اخترت عادةً آخر خلية ، لكنك اخترت أحيانًا خلية عشوائية ، فستكون متاهة معدل التدفق مرتفعًا ، لكن مع حل قصير ومباشر. إذا تم اختيار إحدى الخلايا الأكثر حداثة بشكل عشوائي ، فإن المتاهة لديها معدل تدفق منخفض ، ولكن حل طويل ومتعرج.
• 
  
  تزايد خوارزمية الغابات : هذه خوارزمية أكثر عمومية تجمع بين أنواع تعتمد على الأشجار والمجموعات. إنها امتداد لخوارزمية نمو الأشجار ، والتي تتضمن بشكل أساسي عدة حالات تتوسع في وقت واحد. نبدأ مع جميع الخلايا التي تم فرزها بشكل عشوائي في قائمة "جديدة" ؛ بالإضافة إلى ذلك ، لكل خلية مجموعة خاصة بها ، كما في بداية خوارزمية Kruskal. أولاً ، حدد خلية واحدة أو أكثر عن طريق نقلها من قائمة "جديدة" إلى قائمة "نشطة". حدد خلية من القائمة "النشطة" وقم بقطع المقطع إلى الخلية التالية التي لم يتم إنشاؤها من القائمة "الجديدة" ، وإضافة خلية جديدة إلى قائمة "نشطة" والجمع بين مجموعات خليتين. إذا تم إجراء محاولة لتقطيع الجزء الموجود من المتاهة ، فقم بتمكينه إذا كانت الخلايا في مجموعات مختلفة ودمج الخلايا ، كما يحدث في خوارزمية Kraskal. إذا لم تكن هناك خلايا "جديدة" بالقرب من الخلية الحالية ، فقم بنقل الخلية الحالية إلى قائمة الخلايا "المكتملة". اكتمال المتاهة عندما تصبح قائمة "نشط" فارغة. في النهاية ، نجمع كل المجموعات المتبقية ، كما هو الحال في خوارزمية Kruskal. بشكل دوري ، يمكنك إنشاء أشجار جديدة عن طريق نقل خلية واحدة أو أكثر من قائمة "جديدة" إلى قائمة "نشطة" ، كما حدث في البداية. من خلال التحكم في عدد الأشجار الأصلية ومشاركة الأشجار التي تم إنشاؤها حديثًا ، يمكنك إنشاء العديد من القوام الفريد الذي يجمع مع المعلمات المرنة بالفعل لخوارزمية نمو الأشجار.
• 
  
  خوارزمية Eller : هذه خوارزمية خاصة ، لأنها ليست فقط أسرع من أي شخص آخر ، ولكن ليس لها أيضًا أي تحيز أو عيوب واضحة ؛ بالإضافة إلى ذلك ، عندما يتم إنشاؤه ، يتم استخدام الذاكرة بكفاءة. لا يتطلب الأمر وجود المتاهة بأكملها في الذاكرة ، بل يستخدم وحدة تخزين متناسبة مع حجم الخط. يقوم بإنشاء خط متاهة بسطر ، بعد اكتمال إنشاء السلسلة ، لم تعد الخوارزمية تأخذها في الاعتبار. كل خلية في صف واحد موجود في مجموعة. تنتمي خليتان إلى نفس المجموعة إذا كان هناك مسار بينهما على طول المتاهة التي تم إنشاؤها بالفعل. تتيح لك هذه المعلومات قطع الممرات في السطر الحالي دون إنشاء حلقات أو مناطق معزولة. في الواقع ، إنها تشبه إلى حد كبير خوارزمية Kraskal ، حيث يتم تشكيلها هنا في سطر واحد فقط ، في حين ينظر Kraskal عبر المتاهة بأكملها. يتكون تكوين صف من جزأين: قم بتوصيل الخلايا المجاورة بشكل عشوائي داخل الصف ، أي نقطع الممرات الأفقية ، ثم نربط الخلايا بشكل عشوائي بين الحالي والصف التالي ، أي قطع الممرات العمودية. عند قطع الممرات الأفقية ، لا نقوم بتوصيل الخلايا الموجودة بالفعل في نفس المجموعة (لأنه سيتم إنشاء حلقة على خلاف ذلك) ، وعند قطع الممرات الرأسية ، يجب علينا توصيل خلية إذا كان لها حجم وحدة (لأنه إذا تركتها ، فسوف تنشئ منطقة معزولة). عند قطع الممرات الأفقية ، نقوم بتوصيل الخلايا إذا كانت في نفس المجموعة (لأنه يوجد الآن مسار بينهما) ، وعند قطع الممرات الرأسية عندما لا نتواصل مع الخلية ، نضعها في مجموعة منفصلة (لأنه يتم فصلها الآن عن بقية المتاهة ). يبدأ Creation بحقيقة أنه قبل توصيل الخلايا في الصف الأول ، يكون لكل خلية مجموعة خاصة بها. اكتمال الإنشاء بعد اتصال الخلايا في الصف الأخير. هناك قاعدة خاصة للإكمال: بحلول وقت الانتهاء ، يجب أن تكون كل خلية في نفس المجموعة لتجنب المناطق المعزولة. (يتم إنشاء السطر الأخير من خلال الجمع بين كل من أزواج الخلايا المجاورة التي ليست موجودة في نفس المجموعة بعد.) من الأفضل تنفيذ المجموعة باستخدام قائمة خلايا دورية مزدوجة الخلايا (والتي يمكن أن تكون مجرد مصفوفة تربط الخلايا بأزواج من الخلايا على كلا الجانبين من نفس المجموعة) ، مما يسمح تنفيذ الإدراج والحذف والتحقق من وجود الخلايا المجاورة في مجموعة واحدة لفترة زمنية ثابتة. المشكلة في هذه الخوارزمية هي الخلل في معالجة الحواف المختلفة للمتاهة. لتجنب بقع في القوام ، تحتاج إلى الاتصال وتخطي ربط الخلايا بالنسب الصحيحة.
• 
  
  الانقسام التكراري: تشبه هذه الخوارزمية إلى حد ما التراجع المتكرر ، لأن كلاهما يستخدم مداخن ، فقط لا يعمل مع الممرات ، ولكن مع الجدران. نبدأ بإنشاء جدار أفقي أو عمودي عشوائي يتقاطع مع منطقة يمكن الوصول إليها في صف أو عمود عشوائي ، ويضع مسافات فارغة بشكل عشوائي على طوله. ثم نكرر بشكل متكرر عملية المنطقتين دون الإقليميتين الناتجة عن الجدار الفاصل. للحصول على أفضل النتائج ، تحتاج إلى إضافة انحراف في اختيار الأفقي أو العمودي استنادًا إلى نسب المنطقة ، على سبيل المثال ، المساحة التي يكون عرضها ضعف الارتفاع يجب تقسيمها في كثير من الأحيان بواسطة الجدران الرأسية. هذه هي أسرع خوارزمية بدون انحرافات في الاتجاهات ، وغالبًا ما يمكنها التنافس مع متاهات تعتمد على الأشجار الثنائية ، لأنها تخلق خلايا متعددة في نفس الوقت ، على الرغم من أن لها عيبًا واضحًا في شكل جدران طويلة تتقاطع داخل المتاهة. هذه الخوارزمية هي نوع من المتاهات المدمجة النمطي هندسي متكرر ، ولكن بدلاً من إنشاء متاهات من الخلايا ذات حجم ثابت باستمرار مع متاهات من نفس الحجم داخل كل خلية ، فإنها تقسم عشوائيًا مساحة معينة إلى متاهة من الحجم العشوائي: 1x2 أو 2x1. لا يمكن استخدام القسمة التكرارية لقطع الممرات ، لأن هذا يؤدي إلى إيجاد حل واضح يتبع إما على طول الحافة الخارجية ، أو يتقاطع بشكل مباشر مع الداخل.
• 
  
  المتاهات القائمة على الأشجار الثنائية : في الواقع ، هذه هي أبسط الخوارزميات وأسرعها الممكنة ، ومع ذلك ، فإن المتاهات التي تم إنشاؤها لها نسيج ذو انحياز عالٍ للغاية. بالنسبة لكل خلية ، نقوم بقطع ممر إما لأعلى أو إلى اليسار ، ولكن ليس في كلا الاتجاهين. في الإصدار مع إضافة الجدران ، تتم إضافة مقطع جدار لكل قمة تؤدي إلى أسفل أو إلى اليمين ، ولكن ليس في كلا الاتجاهين. كل خلية مستقلة عن جميع الخلايا الأخرى ، لأننا لسنا بحاجة للتحقق من حالة بعض الخلايا الأخرى عند إنشائها. لذلك ، هذه خوارزمية حقيقية لتوليد المتاهات بدون ذاكرة ، ولا تقتصر على حجم المتاهات التي تم إنشاؤها. في الواقع ، هذه شجرة ثنائية ، إذا أخذنا في الاعتبار الزاوية العليا اليسرى كجذر ، ولكل عقدة أو خلية عقدة أصلية واحدة فريدة ، وهي خلية أعلى أو إلى يسارها. تختلف المتاهات القائمة على الأشجار الثنائية عن المتاهات المثالية القياسية ، لأن أكثر من نصف أنواع الخلايا لا يمكن أن توجد فيها. على سبيل المثال ، لن يكون هناك تقاطعات فيها ، وكل الطرق المسدودة بها ممرات تؤدي إلى اليسار أو إلى اليسار ، ولا تؤدي أبداً إلى أسفل أو إلى اليمين. تميل المتاهات إلى وجود ممرات تؤدي قطريًا من أعلى اليسار إلى أسفل اليمين ، ومن الأسهل بكثير الانتقال من أسفل اليمين إلى أعلى اليسار. يمكنك دائمًا التحرك لأعلى أو إلى اليسار ، ولكن لا يتم ذلك في نفس الوقت في كلا الاتجاهين ، بحيث يمكنك دائمًا التحرك قطريًا للأعلى ولليسار ، دون مواجهة الحواجز. سيكون لديك الفرصة لاختيار الوقوع في طريق مسدود عن طريق تحريك لأسفل وإلى اليمين. , , , .
• 
  
  Sidewinder: , . : , , . , , , , , . , ( , ). , sidewinder . , sidewinder . , sidewinder , , . sidewinder , « ». , sidewinder — , , , , . sidewinder , , , .

خوارزمية	٪ طريق مسدود	نوع	أفضلية	لا انحياز؟	موحدة؟	الذاكرة	وقت	حل ٪
طريق واحد	0	خشب	الجدران	نعم	أبدا	N ^ 2	379	100.0
تراجع متكرر	10	خشب	الممرات	نعم	أبدا	N ^ 2	27	19.0
مطاردة وقتل	11 (21)	خشب	الممرات	نعم	أبدا	0	100 (143)	9.5 (3.9)
تقسيم العودية	23	خشب	الجدران	نعم	أبدا	N *	10	7.2
شجرة ثنائية	25	كثير	على حد سواء	لا	أبدا	0 *	10	2.0
سايد	27	كثير	على حد سواء	لا	أبدا	0 *	12	2.6
خوارزمية إلر	28	كثير	على حد سواء	لا	لا	N *	20	4.2 (3.2)
خوارزمية ويلسون	29	خشب	على حد سواء	نعم	نعم	N ^ 2	48 (25)	4.5
خوارزمية ألدوس برودر	29	خشب	على حد سواء	نعم	نعم	0	279 (208)	4.5
كراسكال الخوارزمية	30	كثير	على حد سواء	نعم	لا	N ^ 2	33	4.1
خوارزمية بريما (حقيقية)	30	خشب	على حد سواء	نعم	لا	N ^ 2	160	4.1
خوارزمية بريما (المبسطة)	32	خشب	على حد سواء	نعم	لا	N ^ 2	59	2.3
خوارزمية بريما (معدلة)	36 (31)	خشب	على حد سواء	نعم	لا	N ^ 2	30	2.3
شجرة تنمو	49 (39)	خشب	على حد سواء	نعم	لا	N ^ 2	48	11.0
الغابات المتنامية	49 (39)	على حد سواء	على حد سواء	نعم	لا	N ^ 2	76	11.0

يلخص هذا الجدول خصائص الخوارزميات لإنشاء متاهات مثالية الموضحة أعلاه. للمقارنة ، تمت إضافة خوارزمية متاهة أحادية المسار (نظريًا ، متاهات أحادية المسار مثالية). شرح العمود:

• : , , , 2D-. . , , , . 10% ( ) 49% ( ). Recursive Backtracker 1%. 66%: .
• : : , , . , , , , . , , .
• : , . . , , . Recursive Backtracker , , , . , , . , Hunt and Kill , , .
• : , . , . Sidewinder , . , . Hunt and Kill , , , .
• : . «» , . «» , , . «» , , . , .
• : , . , , (N), (N^2). , ( ). , , . Sidewinder , . , .
• : , , , . , ( 10), . 100x100 Daedalus. , , , .
• : , , . , 100x100 . . «» . , . , . , , , .

هناك طرق عديدة لحل المتاهات ، ولكل منها خصائصه الخاصة. فيما يلي قائمة بخوارزميات محددة:

• 
  
  متابعة على طول الجدران (أتباع الجدار) : . («»), . ( ). , ( ) . , . , , . , , , . 3D- , 3D- 2D-, .. , -, -, .
• 
  
  : , «» , . 2D- , , .. . , , . . , , . , , . , , . , , — -1, — 1. , , .. 360 , «». , «», , , , , . , , . , — , .
• 
  
  : (Chain algorithm) , ( ) . , , . , . , , . , . ( ) , . . , , . «» , . , , , . , . , .
• 
  
  Recursive backtracker: , . , . : ( ), «», , , «», , . , , «»; «» . (backtracking) , , . , . , , .
• 
  
  (Trémaux's algorithm): . recursive backtracker : , . , . , , . , , , . ( , .) , (.. ), , , , (.. , ). , , , , , . , . , , .
• 
  
  (Dead end filler) : . , . , , . , . , , . , , .
• 
  
  Cul-de-sac filler : , , . dead end filler, , . ( — , , ) , . dead end filler. , , , , . , , , dead end filler.
• 
  
  Blind alley filler : , , . , . — , , . , , cul-de-sac filler, . . , , , , . , , , ( ). , , . , cul-de-sac filler - , collision solver , - .
• 
  
  Blind alley sealer : blind alley filler , , . . . , , blind alley filler, . . , , , , . , , . , . , , . , , .
• 
  
  (Shortest path finder): , , . , , . collision solver, , , «» , ( ), «» , , . «», , . , - , . , , , A* , .
• 
  
  (Shortest paths finder) : , . , , , , , , , - , . , , , «» , , , . , , , , . , .
• Collision solver: "amoeba" solver. . , . «» , ( ). « » ( ), , . «», , , , . ( , «», . , , , .) , shortest paths finder, ( ) ( ).
• Random mouse: , , .. , . 180 , . , , . , , .

		?		?	?	?	?
Random Mouse	1	لا		/	لا	نعم	لا
Wall Follower	1	لا		/	نعم	نعم	نعم
	1	لا		/	نعم	نعم	نعم
	1	نعم	+	لا	نعم	لا	نعم
تراجع متكرر	1	نعم	أنت كذلك	لا	نعم	لا	نعم
خوارزمية تريمو	1	نعم	أنت كذلك	الداخل / انتهى	لا	لا	نعم
حشو مسدود	كل +	لا	تيه	خلال	لا	نعم	نعم
حشو Cul-de-sac	كل +	لا	تيه	خلال	لا	نعم	نعم
أعمى السداده السداده	كل +	نعم	تيه	لا	لا	لا	نعم
أعمى زقاق حشو	جميع	نعم	تيه	خلال	لا	نعم	لا
حل الاصطدام	كل أقصر	نعم	أنت +	لا	لا	لا	نعم
البحث عن أقصر الطرق	كل أقصر	نعم	أنت +	لا	نعم	لا	نعم
البحث عن أقصر الطرق	1 أقصر	نعم	أنت +	لا	نعم	لا	نعم

يسرد هذا الجدول باختصار خصائص خوارزميات حل المتاهة الموضحة أعلاه. وفقًا لهذه المعايير ، من الممكن تصنيف الخوارزميات وتقييمها لحل المتاهات. توضيحات العمود:

• : , . . , () . Dead end filler cul-de-sac filler ( blind alley sealer ) , , , «+».
• : . Random mouse «», , wall follower «», , . dead end filler cul-de-sac filler «», .
• : : «» ( ) . , ( «») («+») . , .
• : , , . , «», , ( ), , , , . .
• : . , , , , . Wall follower, . Recursive backtracker shortest path(s) finder .
• : . .
• سريع: هل تعتبر عملية اتخاذ القرار سريعة. تعد الخوارزميات الأكثر كفاءة كافية للنظر إلى كل خلية من المتاهة مرة واحدة فقط ، أو يمكنها تخطي أجزاء منها بالكامل. يجب أن يكون وقت التشغيل متناسبا مع حجم المتاهة ، أو O (n ^ 2) ، حيث n هو عدد الخلايا على جانب واحد. يكون الماوس العشوائي بطيئًا لأن اكتماله غير مضمون ، ويحتمل أن تعمل حشو الزقاق العمياء على حل المتاهة من كل شوكة.

عمليات أخرى مع المتاهات

بالإضافة إلى إنشاء متاهات وحلها ، يمكنك إجراء عمليات أخرى معهم:

• 
  
  : « », , Fill FloodFill. FloodFill , , . , , FloodFill , . , , FloodFill , , . «» .
• 
  
  (Isolation remover): , , . , . , . ( , ) , . , , . .
• 
  
  : , , . , , . , . ( , ) . , , , . , .
• 
  
  : , . , , , , . , , . , . , blind alley sealer ( , ). , , .

• Daedalus : Daedalus, Windows. Daedalus .