علم جوجولوجيا (هذا ليس خطأ مطبعي) للمبرمجين

من الصعب الكتابة عن الرياضيات (بحيث تكون مثيرة للاهتمام) أكثر من الكتابة عن الفيزياء. ومع ذلك ، أتمنى أن تقرأ على الأقل أمثلة لبرامج C المجنونة.


يمكن أن تنمو الوحوش من أشياء غير ضارة تمامًا. خذ ، على سبيل المثال ، لعبة الأوتار الفرعية. نكتب سلسلة من الحروف a و b ونختار الخطوط الفرعية من الحرف 1 إلى الحرف 2 ، من 2 إلى 4 ، من 3 إلى 6 ، من n إلى 2n ، حتى طول السلسلة الرئيسية يكفي. مهمتنا هي التأكد من أن الأقصر لا يدخل في هذه الأسطح. حتى كتبت محلل SQL:

declare @s varchar(max) = 'abbbaaaaaaab' declare @n int=1 declare @sub table (n int, sub varchar(max)) while @n*2<=len(@s) begin insert into @sub select @n,substring(@s,@n,@n+1) set @n=@n+1 end select *,(select max(sub) from @sub I where In>On and charindex(O.sub,I.sub)>0) as FoundMatch from @sub O order by 1 

هنا مثال الإخراج:



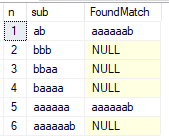
كما ترون ، لم ينجح الاختبار الفرعي 1 و 5 في الاختبار. يمكننا إزالة الشخصية الأخيرة ، وستجتاز السلسلة المكونة من 11 حرفًا "abbbaaaaaaaa" الاختبار. اتضح أن هذا هو أطول سلسلة ممكنة في الأبجدية المكونة من حرفين والتي تفي بهذا الشرط.

بالنسبة للحروف الأبجدية ذات الحرف الواحد ، يبلغ الحد الأقصى لطول السلسلة 3 ، ثم لأسباب فنية بحتة. اتضح أن الحد الأقصى للطول محدود للأبجدية لأي عدد من الحروف. لذلك لدينا:

$$

$$f (1) = 3$$

$$

$$f (2) = 11$$

$$

$$f (3) = ؟؟؟$$

اختبر الحدس الخاص بك حول المدة التي يمكن أن يتم بها سلسلة الحروف الأبجدية المكونة من ثلاثة أحرف. 100؟ 1000؟ في الواقع ، أكثر بكثير من Googol ، وأكثر بكثير من GoogolPlekh.

$$

$$f (3)> 2 \ uparrow ^ {7198} 158836$$

ولا بد لي من قضاء بعض الوقت لإظهار قوة الرماة.

السهام (فرط الحركة)

نستخدم الضرب حتى لا نكتب العديد من عمليات الإضافة:

$$

$$2 * 5 = 2 + 2 + 2 + 2 + 2$$

نستخدم الأس الأسى حتى لا نكتب العديد من الضرب:

$$

$$2 ^ 3 = 2 * 2 * 2$$

بالنظر إلى الإضافة كعملية من المستوى 0 ، الضرب على 1 ، الأس على 2 ، يمكننا تقديم العملية "السهم" ، على سبيل المثال ،

$$

$$3 \ uparrow 3 = 3 ^ {(3 ^ 3)} = 3 ^ {27} = 7'625'597'484'987$$

لاحظ أن الأقواس مهمة بالفعل هنا. المستوى التالي هو عملية السهمين:

$$

$$3 \ uparrow \ uparrow 3 = 3 \ uparrow (3 \ uparrow 3) = 3 \ uparrow 7625597484987 = 3 ^ {3 ^ {... ^ 3}}$$

يبلغ ارتفاع الهرم الأخير من ثلاثة أضعاف 7 مليارات دولار ، وهذا العدد أكبر بكثير بالفعل من googolple و googolpleks. نشير إلى هذا الرقم الضخم باسم Darkness (كان رقمًا كبيرًا باللغة الروسية القديمة) ونحاول اتخاذ خطوة أخرى:

$$

$$3 \ uparrow ^ 3 3 = 3 \ uparrow \ uparrow \ uparrow 3 = 3 \ uparrow \ uparrow (3 \ uparrow \ uparrow 3) = 3 \ uparrow \ uparrow {darkness} = 3 \ uparrow 3 \ uparrow 3 ... \ uparrow 3 دولا$$

(ومرات عديدة) ... هناك بالفعل تخيل حجم هذا العدد. يرجى ملاحظة أنه عندما يكون هناك الكثير من الأسهم ، نكتب مكرر في الأعلى. حتى تتمكن من فهم كم هو عظيم

$$

$$f (3)> 2 \ uparrow ^ {7198} 158836$$

و اكثر

باستخدام الأسهم ، يتم إنشاء فقط أصغر الأرقام الكبيرة ، إذا جاز التعبير. يتم قياس معدل نمو الوظائف على نطاق معين - من خلال المقارنة مع الوظائف سريعة النمو . تتوافق الوظيفة الأولى في هذا التسلسل الهرمي مع الإضافة ، والثانية في الضرب ، والثالثة للسهم ، والسهم من n إلى n-2 (تقريبًا ، وليس بالضبط). ولكن يمكنك تحديد

$$

$$f_w (n) = f_n (n)$$

مثل هذه الوظيفة لـ n = 3 قابلة للمقارنة بسهم واحد ، بالنسبة لـ n = 4 بسهمين ، ومع نمو المعلمة n ، تفوق نمو الوظيفة مع أي عدد ثابت من الأسهم.

يمكنك الذهاب أبعد من ذلك: $$$f_w ، f_ {w + 1} ، f_ {w + n} ، f_ {w2} ، f_ {w ^ 2} ، f_ {w ^ w} ، f_ {w ^ {w ^ {w} {}} ، f_ \ epsilon$ يتم فهرسة هذه الوظائف بواسطة المراسيم ، أو في الأدب الروسي بالأرقام الترتيبية. الصورة مع بنية الأعداد الترتيبية الأولية تسبق المقالة ، لكنها تمتد إلى أبعد من ذلك بكثير ، وتبدأ كذلك

التصوف قليلا

هرم أوميغا الذي لا نهاية له يعطي ترتيبي $$$\ epsilon_0$ . اقرأ عن الوظيفة التي يقاس نموها بهذا الترتيبي. اتضح أن الوظيفة تنمو بسرعة كبيرة بحيث لا يمكن للحساب الرسمي أن يثبت من حيث المبدأ أن هذه الوظيفة محددة على الإطلاق!

بالطبع ، أنت تعرف عن نظرية غودل أن هناك تصريحات غير قابلة للإثبات. ولكن كقاعدة عامة ، فإن المثال الوحيد لمثل هذا البيان هو بناء غودل نفسه ("أنا غير قابل للإثبات"). نظرية جودستين مثال جيد على مثل هذا التصريح.

علاوة على ذلك ، اتضح أن القوانين التقليدية تقيس بطريقة ما قوة النظريات . "قوة" الحساب الرسمي هو $$$\ epsilon_0$ تمتلك نظرية مجموعة Kripke-Plateka المبسطة قوة ترتيبي Feferman-Schutte ، إلخ.

مسابقة القصدير - الرياضيات - مسابقة اللغة

عقدت مسابقة لتوليد أعداد كبيرة. لا ، لا تزال البرمجة لجهاز تورينج قاسية للغاية ، لذلك تم استخدام C لبعض الآلات اللانهائية المجردة ذات الحجم (int) = اللانهاية. يمكنك أيضًا استخدام malloc () ، ومقدار الذاكرة ، مثل المكدس ، غير محدود. كان طول البرنامج فقط محدودًا - كان يجب أن يتناسب البرنامج مع 512 بايت (باستثناء المسافات) ، ولكن تم السماح باستخدام المعالج المسبق (#define).

يتم نشر النتائج على موقع الرياضيات . في نفس الوقت تحقق من تصميم موقع عالم الرياضيات الحقيقي. النتائج هنا . هنا هو نص البرنامج ، الذي احتل المرتبة الثانية ، مع إعطاء الرقم عنه

$$

$$f_ {w ^ w} (10 ^ {500})$$

 typedef int J; JP(J x,J y) { return x+y ? x%2 + y%2*2 + P(x/2,y/2)*4 : 0 ;} JH(J z) { return z ? z%2 + 2*H(z/4) : 0 ;} JI(J f,J e,J r){ return f ? P(P(f,e),r) : r ;} JM(J x,J e) { return x ? I(x%2, M(e,0), M(x/2, e+1)) : 0 ;} JD(J,J); JE(J f,J e,J r,J b) { return e ? E(1, D(e,b), I(b-1, D(e,b), I(f-1,e,r)), b) : I(f-1,e,r) ; } JD(J x,J b) { return x ? E( H(H(x)), H(H(x)/2), H(x/2), b) : 0 ;} JF(J x,J b) { return x ? F(D(x,b+1),b+1) : b ;} JG(J x) { return F(M(x,9), 9) ;} J f(J n,J x) { return n ? f(n-1, G(x ? f(n,x-1) : n)) : G(x) ;} J g(J x) { return f(x,x) ;} J h(J n,J x) { return n ? h(n-1, g(x ? h(n,x-1) : n)) : g(x) ;} J main(void) { return h(g(9),9) ;} 

نص برنامج الفائز أطول ، وأردت فقط أن أوضح من أين يبدأ:

 #define R { return #define PP ( #define LL ( #define TS (v, y, c, #define C ), #define X x) #define F );} 

ولكن حتى منظم المسابقة وجد أنه من الصعب تقييم حجم العدد الكبير (المكتوب جدًا )

القنادس مشغول

حسنًا ، يكفي للتعامل مع الأعداد الصغيرة ، لنقم بأعداد كبيرة. تخيل أنه تم تنظيم مسابقة عالمية لكتابة برنامج لتوليد أكبر عدد. نظرًا لأن عدد البرامج لم يعد يتجاوز 512 حرفًا ، بالطبع ، هناك دائمًا فائز مطلق. لنقم بتعيينها على أنها BB (512) - وظيفة سمور مشغول .

من الواضح أن BB (1024) >> BB (512). لكن ما مدى سرعة نمو وظيفة BB؟ اتضح أنه ينمو بشكل أسرع من كل شيء قابلناه. وظيفة BB نفسها غير قابلة للحل خوارزميًا ؛ لا يمكن حسابها على جهاز كمبيوتر. ولكن مع زيادة طول البرنامج الصحيح ، يمكننا تنفيذ المزيد والمزيد من الأفكار الجديدة. BB ينمو بشكل أسرع من أي وظيفة قابلة للحساب من الناحية الحسابية.

قدم كبير

حسنًا ، يكفي للتعامل مع الأعداد الصغيرة ، لنقم بأعداد كبيرة. آه ، هل قلت ذلك بالفعل؟ سيكون من الرائع تشغيل BB (BB (n)). ولكن نظرًا لأن BB غير قابل للحساب ، فهناك صعوبات تقنية في هذا (مثل هذه الوظيفة قابلة للحساب في أجهزة Turing مع أوراكل - وليس الخلط بين أوراكل مع Oracle DBMS).

ولكن يمكنك القيام بذلك بشكل أسهل ، بدلاً من البرنامج ، فكر في صيغة ذات مقاييس طولية n. لا تعد صيغة الكمي مهمة إذا كان هناك شيء يمكن حسابه أم لا. بحيث يمكنك على الأقل شغل الوظيفة BB (1،000،000،000) ، وتطبيقها على نفسك BB (BB (BB (1،000،000))) مرات. وهذا فقط ما يتبادر إلى الذهن لأول مرة.

يُشار إلى أكبر عدد يمكن ترقيمه بواسطة صيغة تتكون من أكثر من حرف n بالرمز FOOT (n).

$$

$$BIG FOOT = FOOT ^ {10} (10 ^ {100})$$

PS

بالنسبة للمقال التالي ، أود أن أفهم ما يجب التركيز عليه ، والمشاركة في الاستبيان من فضلك