🎏 👗 🤛🏼 انخفاض في حجم عينة من البيانات التجريبية دون فقدان المعلومات 🛫 🧛 🌵

ما هي مشكلة الرسوم البيانية البيانات التجريبية

أساس إدارة جودة المنتج لأي مؤسسة صناعية هو جمع البيانات التجريبية مع معالجتها اللاحقة.

تتضمن المعالجة الأولية للنتائج التجريبية مقارنة الفرضيات حول قانون توزيع البيانات ، والتي تصف ، مع أصغر خطأ ، متغيرًا عشوائيًا على العينة المرصودة.

لهذا ، يتم تقديم العينة في شكل رسم بياني يتكون من

ك

$ك$ الأعمدة التي شيدت على فترات من الطول

د

$د$ .

يتطلب تحديد شكل توزيع نتائج القياس أيضًا عددًا من المشكلات التي تختلف كفاءة حلها بالنسبة لتوزيعات مختلفة (على سبيل المثال ، باستخدام طريقة المربعات الصغرى أو حساب تقديرات الإنتروبيا).

بالإضافة إلى ذلك ، يعد تحديد التوزيع ضروريًا أيضًا لأن تناثر جميع التقديرات (الانحراف المعياري ، الزائد ، التقرن ، إلخ) يعتمد أيضًا على شكل قانون التوزيع.

يعتمد نجاح تحديد شكل توزيع البيانات التجريبية على حجم العينة ، وإذا كانت صغيرة ، فإن ميزات التوزيع يتم حجبها بواسطة العشوائية للعينة نفسها. في الممارسة العملية ، لا يمكن توفير حجم عينة كبير ، على سبيل المثال ، أكثر من 1000 ، لأسباب مختلفة.

في مثل هذه الحالة ، من المهم توزيع بيانات العينة بأفضل طريقة في الفواصل الزمنية ، عندما تكون سلسلة الفاصل ضرورية لمزيد من التحليل والحسابات.

لذلك ، من أجل التحديد الناجح ، من الضروري حل مشكلة تعيين عدد الفواصل k

أ. يقنع Hald في الكتاب [1] على نطاق واسع أن هناك عددًا مثاليًا من الفواصل الزمنية للتجميع عندما يكون الغلاف التدريجي للرسم البياني المبني على هذه الفواصل الأقرب إلى منحنى التوزيع السلس للجمهور العام.

واحدة من العلامات العملية لمقاربة الأمثل هي اختفاء الانخفاضات في الرسم البياني ، ثم يعتبر أعظم ك بالقرب من الأمثل ، حيث لا يزال الرسم البياني يحتفظ بطابع سلس.

من الواضح أن نوع الرسم البياني يعتمد على بناء فواصل الانتماء إلى متغير عشوائي ، ومع ذلك ، حتى في حالة وجود قسم موحد ، لا تزال طريقة مرضية لهذا البناء غير متوفرة.

يؤدي القسم ، الذي يمكن اعتباره صحيحًا ، إلى أن الحد الأدنى من الخطأ التقريبي الناتج عن الوظيفة الثابتة تدريجياً لكثافة التوزيع المستمرة المفترضة (الرسم البياني) سيكون ضئيلاً.

وتكمن الصعوبات في حقيقة أن الكثافة المقدرة غير معروفة ؛ وبالتالي ، فإن عدد الفواصل الزمنية يؤثر بشدة على شكل توزيع تردد العينة النهائية.

بالنسبة لطول العينة الثابت ، لا يؤدي توسيع فواصل التقسيم إلى تحسين الاحتمال التجريبي للدخول إليها ، بل يؤدي أيضًا إلى فقد المعلومات بشكل لا مفر منه (بالمعنى العام ومعنى منحنى توزيع الكثافة الاحتمالية) ، وبالتالي ، مع زيادة التوسيع غير المبررة ، فإن التوزيع الذي تمت دراسته .

بمجرد نشأتها ، لا تختفي مهمة التقسيم الأمثل للنطاق الموجود تحت الرسم البياني من مجال رؤية المتخصصين ، وإلى أن يظهر الرأي الثابت الوحيد بشأن حلها ، ستظل المهمة ذات صلة.

اختيار معايير لتقييم جودة الرسم البياني للبيانات التجريبية

يتطلب معيار بيرسون ، كما هو معروف ، تقسيم العينة إلى فواصل زمنية - حيث يتم تقييم الفرق بين النموذج المعتمد والعينة المقارنة.

c h i^{2} = s u m_{j = 1}^{m} f r a c (E_{j} - M_{j})^{2} M_{j}

$\ chi ^ {2} = \ sum_ {j = 1} ^ {m} \ frac {(E_ {j} -M_ {j}) ^ {2}} {M_ {j}}$

حيث:

E_{j}

$E_ {j}$ - الترددات التجريبية

(n_{j})

$(n_ {j})$ .

M_{j}

$M_ {j}$ - قيم التردد في نفس العمود ؛ عدد أعمدة المدرج الإحصائي.

ومع ذلك ، فإن تطبيق هذا المعيار في حالة الفواصل الزمنية ذات الطول الثابت ، والذي يستخدم عادةً لإنشاء مدرج تكراري ، غير فعال. لذلك ، في الأعمال المتعلقة بفعالية معيار Pearson ، لا تعتبر الفواصل الزمنية متساوية الطول ، ولكن باحتمالية متساوية وفقًا للنموذج المقبول.

ومع ذلك ، في هذه الحالة ، يختلف عدد الفواصل الزمنية ذات الطول المتساوي وعدد الفترات ذات الاحتمال المتساوي عدة مرات (باستثناء التوزيع المحتمل على قدم المساواة) ، مما يسمح للمرء بالشك في موثوقية النتائج التي تم الحصول عليها في [2].

كمعيار قرب ، من المستحسن استخدام معامل الانتروبيا ، والذي يتم حسابه على النحو التالي [3]:

k_{e} = f r a c d n 2 s i g m a 10^{b e t a}

$k_ {e} = \ frac {dn} {2 \ sigma} 10 ^ {\ beta}$

b e t a = - f r a c 1 n s u m_{i = 1}^{m} n_{i} l g (n_{i})

$\ beta = - \ frac {1} {n} \ sum_ {i = 1} ^ {m} {n_ {i} lg (n_ {i})}$

حيث:

n_{i}

$n_ {i}$ - عدد الملاحظات في الفاصل الأول

i = 0 ، . . . ، m

$i = 0 ، ... ، m$

خوارزمية لتقييم جودة الرسم البياني للبيانات التجريبية باستخدام معامل الانتروبيا ووحدة الرسم البياني numpy.histogram

بناء جملة استخدام الوحدة النمطية هو كما يلي [4]:

numpy.histogram (a ، bins = m ، range = None ، normed = None ، الأوزان = بلا ، الكثافة = بلا)

سننظر في طرق لإيجاد العدد الأمثل m لفواصل تقسيم الرسم البياني المطبقة في وحدة numpy.histogram:

• "تلقائي" - توفر أقصى درجات لـ "sturges" و "fd" أداءً جيدًا ؛
• 'fd' (مقيم Freedman Diaconis) - مقيم موثوق (مقاوم للانبعاثات) يأخذ في الاعتبار تباين البيانات وحجمها ؛
• "doane" - هناك نسخة محسنة من عمليات التطهير التي تعمل بشكل أكثر دقة مع مجموعات البيانات ذات التوزيع غير الطبيعي ؛
• "scott" هو مقيم أقل موثوقية يأخذ في الاعتبار تباين وحجم البيانات ؛
• "حجر" - يعتمد المقيِّم على فحص تقديري لتقدير مربع الخطأ ، ويمكن اعتباره بمثابة تعميم لقاعدة سكوت ؛
• "الأرز" - لا يأخذ المثمن في الاعتبار التباين ، ولكن فقط حجم البيانات ، غالباً ما يبالغ في تقدير عدد الفواصل الزمنية المطلوبة ؛
• 'sturges' - طريقة (افتراضياً) تأخذ في الاعتبار حجم البيانات فقط ، وهي مثالية فقط للبيانات الغوسية وتقلل من تقدير عدد الفواصل الزمنية لمجموعات البيانات الكبيرة غير الغوسية ؛
• 'sqrt' هو مقدر الجذر التربيعي لحجم البيانات التي يستخدمها Excel والبرامج الأخرى لإجراء عمليات حسابية سريعة وسهلة لعدد الفواصل الزمنية.

لبدء وصف الخوارزمية ، نقوم بتكييف الوحدة النمطية numpy.histogram () لحساب معامل الإنتروبيا وخطأ الإنتروبي:

from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#       m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#  ke=h/std (a)#    (1). return ke,h

الآن النظر في المراحل الرئيسية للخوارزمية:

1) نحن نشكل عينة تحكم (يشار إليها فيما يلي باسم "العينة الكبيرة") التي تلبي متطلبات الخطأ في معالجة البيانات التجريبية . من عينة كبيرة ، من خلال إزالة جميع الأعضاء الفردية ، نقوم بتكوين عينة أصغر (يشار إليها فيما يلي باسم "العينة الصغيرة") ؛

2) بالنسبة لجميع المقيّمين ، "تلقائي" ، و "fd" ، و "doane" ، و "scot" ، و "stone" ، و "sturges" ، و "sqrt" ، نحسب معامل الانتروبيا ke1 والخطأ h1 من عينة كبيرة ومعامل الكون ke2 والخطأ h2 لعينة صغيرة ، وكذلك القيمة المطلقة للفرق - القيمة المطلقة (ke1-ke2) ؛

3) التحكم في القيم العددية للمقيّمين على مستوى أربع فترات على الأقل ، نختار المقيِّم الذي يوفر الحد الأدنى لقيمة الفرق المطلق - القيمة المطلقة (ke1-ke2).

4) لاتخاذ القرار النهائي بشأن اختيار المثمن ، نبني على رسم بياني واحد توزيعات للعينات الكبيرة والصغيرة مع المثمن توفير الحد الأدنى قيمة القيمة المطلقة (ke1-ke2) ، وعلى الثاني مع المثمن توفير أقصى قيمة القيمة المطلقة (ke1-ke2). يؤكد ظهور قفزات إضافية في عينة صغيرة في الرسم البياني الثاني على الاختيار الصحيح للمقيم في الأول.

النظر في عمل الخوارزمية المقترحة على عينة من البيانات من منشور [2]. تم الحصول على البيانات عن طريق اختيار عشوائي 80 الفراغات من 500 مع القياس اللاحق للكتلة. يجب أن يكون للكتلة كتلة في الحدود التالية:

m = 17_{- 0.4}^{+ 0.6}

$m = 17 _ {- 0.4} ^ {+ 0.6}$ كغم. نحدد معلمات الرسم البياني الأمثل باستخدام القائمة التالية:

إدراج

 import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#      m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#   ke=h/std (a)#  return ke,h a =array([17.37, 17.06, 16.96, 16.83, 17.34, 17.45, 17.60, 17.30, 17.02, 16.73, 17.08, 17.28, 17.08, 17.21, 17.29,17.47, 16.84, 17.39, 16.95, 16.92, 17.59, 17.28, 17.31, 17.25, 17.43,17.30, 17.18, 17.26, 17.19, 17.09,16.61, 17.16, 17.17, 17.06, 17.09,16.83, 17.17, 17.06, 17.59, 17.37,17.09, 16.94, 16.76, 16.98, 16.70, 17.27, 17.48, 17.21, 16.74, 17.12,17.33, 17.15, 17.56, 17.45, 17.49,16.94, 17.28, 17.09, 17.39, 17.05, 16.97, 17.16, 17.38, 17.23, 16.87,16.84, 16.94, 16.90, 17.27, 16.93,17.25, 16.85, 17.41, 17.37, 17.50,17.13, 17.16, 17.05, 16.68, 17.56 ] ) c=['auto','fd','doane','scott','stone','rice','sturges','sqrt'] n=len(a) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] n1=len(b) print("     (n=80) : %s"%round(std(a),3)) print("    (n=80):%s"%round(mean(a),3)) print("     (n=40): %s"%round(std(b),3)) print("   (n=40): %s"%round(mean(b),3)) u=[] for m in c: ke1,h1=diagram(a,m,n) ke2,h2=diagram(b,m,n1) u.append(abs(ke1-ke2)) print("ke1=%s,h1=%s,ke2=%s,h2=%s,dke=%s,m=%s"%(round(ke1,3),round(h1,3),round(ke2,3),round(h2,3),round(abs(ke1-ke2),3),m)) u1=min(u) c1=c[u.index(min(u))] u2=max(u) c2=c[u.index(max(u))] plt.title(' : %s \n    abs(ke1-ke2) :%s '%(c1,round(u1,3))) plt.hist(a,bins=str(c1)) plt.hist(b,bins=str(c1)) plt.grid() plt.show() plt.title('  : %s \n    abs(ke1-ke2):%s '%(c2,round(u2,3))) plt.hist(a,bins=str(c2)) plt.hist(b,bins=str(c2)) plt.grid() plt.show()

نحصل على:

الانحراف المعياري للعينة (ن = 80): 0.24
التوقع الرياضي للعينة (ن = 80): 17.158
الانحراف المعياري للعينة (ن = 40): 0.202
التوقع الرياضي للعينة (ن = 40): 17.138
ke1 = 1.95 ، h1 = 0.467 ، ke2 = 1.917 ، h2 = 0.387 ، dke = 0.033 ، m = تلقائي
ke1 = 1.918 ، h1 = 0.46 ، ke2 = 1.91 ، h2 = 0.386 ، dke = 0.008 ، m = fd
ke1 = 1.831 ، h1 = 0.439 ، ke2 = 1.917 ، h2 = 0.387 ، dke = 0.086 ، m = doane
ke1 = 1.918 ، h1 = 0.46 ، ke2 = 1.91 ، h2 = 0.386 ، dke = 0.008 ، m = scott
ke1 = 1.898 ، h1 = 0.455 ، ke2 = 1.934 ، h2 = 0.39 ، dke = 0.036 ، m = الحجر
ke1 = 1.831 ، h1 = 0.439 ، ke2 = 1.917 ، h2 = 0.387 ، dke = 0.086 ، m = الأرز
ke1 = 1.95 ، h1 = 0.467 ، ke2 = 1.917 ، h2 = 0.387 ، dke = 0.033 ، m = sturges
ke1 = 1.831 ، h1 = 0.439 ، ke2 = 1.917 ، h2 = 0.387 ، dke = 0.086 ، m = sqrt

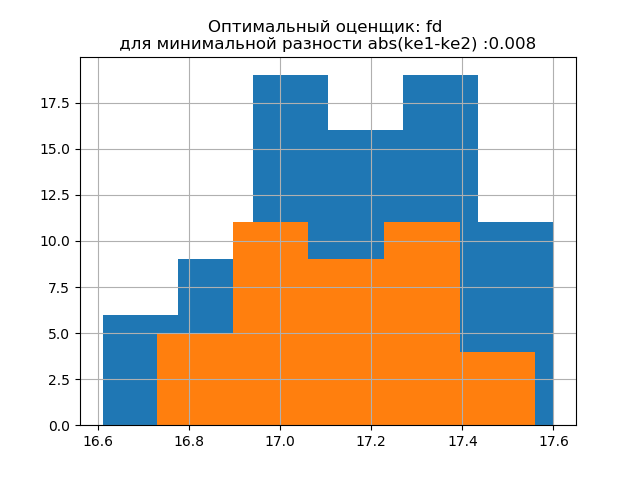
يشبه شكل توزيع عينة كبيرة شكل توزيع عينة صغيرة. كما يلي من البرنامج النصي ، 'fd' هو مقيم موثوق (مقاوم للانبعاثات) يأخذ في الاعتبار تباين البيانات وحجمها. في هذه الحالة ، ينخفض خطأ الإنتروبي للعينة الصغيرة بشكل طفيف: h1 = 0.46 ، h2 = 0.386 مع انخفاض طفيف في معامل الإنتروبيا من k1 = 1.918 إلى k2 = 1.91.

تختلف أنماط توزيع العينات الكبيرة والصغيرة. كما يوحي الوصف ، "doane" هو نسخة محسنة من نقاط "sturges" التي تعمل بشكل أفضل مع مجموعات البيانات ذات التوزيع غير العادي. في كلتا العينات ، يكون معامل الانتروبيا قريبًا من اثنين ، والتوزيع قريب من المعدل الطبيعي ، ويشير ظهور قفزات إضافية في عينة صغيرة في هذا الرسم البياني ، مقارنةً بالعينة السابقة ، إلى الاختيار الصحيح للمقيم "fd" .

نقوم بإنشاء عينتين جديدتين للتوزيع العادي مع المعلمات mu = 20 ، و سيجما = 0.5 والحجم = 100 باستخدام العلاقة:

 a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)])

تنطبق الطريقة المطورة على العينة التي تم الحصول عليها باستخدام البرنامج التالي:

إدراج

 import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#      m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#   ke=h/std (a)#  return ke,h #a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)]) a=array([20.525, 20.923, 18.992, 20.784, 20.134, 19.547, 19.486, 19.346, 20.219, 20.55, 20.179,19.767, 19.846, 20.203, 19.744, 20.353, 19.948, 19.114, 19.046, 20.853, 19.344, 20.384, 19.945,20.312, 19.162, 19.626, 18.995, 19.501, 20.276, 19.74, 18.862, 19.326, 20.889, 20.598, 19.974,20.158, 20.367, 19.649, 19.211, 19.911, 19.932, 20.14, 20.954, 19.673, 19.9, 20.206, 20.898, 20.239, 19.56,20.52, 19.317, 19.362, 20.629, 20.235, 20.272, 20.022, 20.473, 20.537, 19.743, 19.81, 20.159, 19.372, 19.998,19.607, 19.224, 19.508, 20.487, 20.147, 20.777, 20.263, 19.924, 20.049, 20.488, 19.731, 19.917, 19.343, 19.26,19.804, 20.192, 20.458, 20.133, 20.317, 20.105, 20.384, 21.245, 20.191, 19.607, 19.792, 20.009, 19.526, 20.37,19.742, 19.019, 19.651, 20.363, 21.08, 20.792, 19.946, 20.179, 19.8]) c=['auto','fd','doane','scott','stone','rice','sturges','sqrt'] n=len(a) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] n1=len(b) print("     (n=100):%s"%round(std(a),3)) print("    (n=100):%s"%round(mean(a),3)) print("     (n=50):%s"%round(std(b),3)) print("   (n=50): %s"%round(mean(b),3)) u=[] for m in c: ke1,h1=diagram(a,m,n) ke2,h2=diagram(b,m,n1) u.append(abs(ke1-ke2)) print("ke1=%s,h1=%s,ke2=%s,h2=%s,dke=%s,m=%s"%(round(ke1,3),round(h1,3),round(ke2,3),round(h2,3),round(abs(ke1-ke2),3),m)) u1=min(u) c1=c[u.index(min(u))] u2=max(u) c2=c[u.index(max(u))] plt.title(' : %s \n    abs(ke1-ke2) :%s '%(c1,round(u1,3))) plt.hist(a,bins=str(c1)) plt.hist(b,bins=str(c1)) plt.grid() plt.show() plt.title('  : %s \n    abs(ke1-ke2):%s '%(c2,round(u2,3))) plt.hist(a,bins=str(c2)) plt.hist(b,bins=str(c2)) plt.grid() plt.show()

نحصل على:
الانحراف المعياري للعينة (ن = 100): 0.524
التوقع الرياضي للعينة (ن = 100): 19.992
الانحراف المعياري للعينة (ن = 50): 0.462
التوقع الرياضي للعينة (ن = 50): 20.002
ke1 = 1.979 ، h1 = 1.037 ، ke2 = 2.004 ، h2 = 0.926 ، dke = 0.025 ، m = تلقائي
ke1 = 1.979 ، h1 = 1.037 ، ke2 = 1.915 ، h2 = 0.885 ، dke = 0.064 ، m = fd
ke1 = 1.979 ، h1 = 1.037 ، ke2 = 1.804 ، h2 = 0.834 ، dke = 0.175 ، m = doane
ke1 = 1.943 ، h1 = 1.018 ، ke2 = 1.934 ، h2 = 0.894 ، dke = 0.009 ، m = scott
ke1 = 1.943 ، h1 = 1.018 ، ke2 = 1.804 ، h2 = 0.834 ، dke = 0.139 ، m = الحجر
ke1 = 1.946 ، h1 = 1.02 ، ke2 = 1.804 ، h2 = 0.834 ، dke = 0.142 ، m = الأرز
ke1 = 1.979 ، h1 = 1.037 ، ke2 = 2.004 ، h2 = 0.926 ، dke = 0.025 ، m = sturges
ke1 = 1.946 ، h1 = 1.02 ، ke2 = 1.804 ، h2 = 0.834 ، dke = 0.142 ، m = sqrt

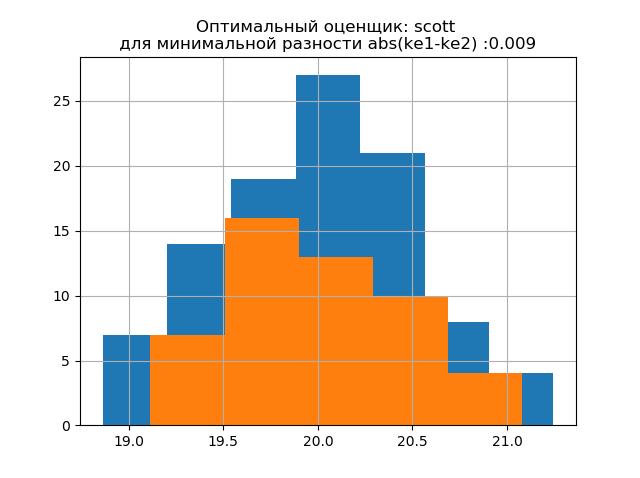
يشبه شكل توزيع عينة كبيرة شكل توزيع عينة صغيرة. كما يلي من الوصف ، يعد "scott" مقيمًا أقل موثوقية يأخذ في الاعتبار تباين البيانات وحجمها. في هذه الحالة ، ينخفض خطأ الإنتروبي لعينة صغيرة بشكل طفيف: h1 = 1.018 و h2 = 0.894 مع انخفاض طفيف في معامل الإنتروبيا من k1 = 1.943 إلى k2 = 1.934. . تجدر الإشارة إلى أنه بالنسبة للعينة الجديدة ، حصلنا على نفس الميل لتغيير المعلمات كما في المثال السابق.

تختلف أنماط توزيع العينات الكبيرة والصغيرة. كما يلي من الوصف ، 'doane' هو نسخة محسنة من تقدير 'sturges' ، والذي يعمل بشكل أكثر دقة مع مجموعات البيانات ذات التوزيع غير العادي. في كلا العينات ، التوزيع طبيعي. يشير ظهور قفزات إضافية في عينة صغيرة على هذا الرسم البياني مقارنةً بالعينة السابقة بالإضافة إلى الاختيار الصحيح للمقيم "سكوت" .

استخدام مكافحة التعرج للتحليل المقارن للرسم البياني

يتيح لك تجانس الرسوم البيانية المبنية على العينات الكبيرة والصغيرة تحديد هويتهم بدقة أكبر من وجهة نظر الحفاظ على المعلومات الموجودة في عينة أكبر. تخيل آخر رسومات بيانية كوظائف تجانس:

إدراج

 from numpy import* from scipy.interpolate import UnivariateSpline from matplotlib import pyplot as plt a =array([20.525, 20.923, 18.992, 20.784, 20.134, 19.547, 19.486, 19.346, 20.219, 20.55, 20.179,19.767, 19.846, 20.203, 19.744, 20.353, 19.948, 19.114, 19.046, 20.853, 19.344, 20.384, 19.945, 20.312, 19.162, 19.626, 18.995, 19.501, 20.276, 19.74, 18.862, 19.326, 20.889, 20.598, 19.974,20.158, 20.367, 19.649, 19.211, 19.911, 19.932, 20.14, 20.954, 19.673, 19.9, 20.206, 20.898, 20.239, 19.56,20.52, 19.317, 19.362, 20.629, 20.235, 20.272, 20.022, 20.473, 20.537, 19.743, 19.81, 20.159, 19.372, 19.998,19.607, 19.224, 19.508, 20.487, 20.147, 20.777, 20.263, 19.924, 20.049, 20.488, 19.731, 19.917, 19.343, 19.26,19.804, 20.192, 20.458, 20.133, 20.317, 20.105, 20.384, 21.245, 20.191, 19.607, 19.792, 20.009, 19.526, 20.37,19.742, 19.019, 19.651, 20.363, 21.08, 20.792, 19.946, 20.179, 19.8]) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] plt.title('    \n  abs(ke1-ke2)' ,size=12) z=histogram(a, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=100') z=histogram(b, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=50') plt.legend(loc='best') plt.grid() plt.show() plt.title('    \n  abs(ke1-ke2)' ,size=12) z=histogram(a, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=100') z=histogram(b, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=50') plt.legend(loc='best') plt.grid() plt.show()

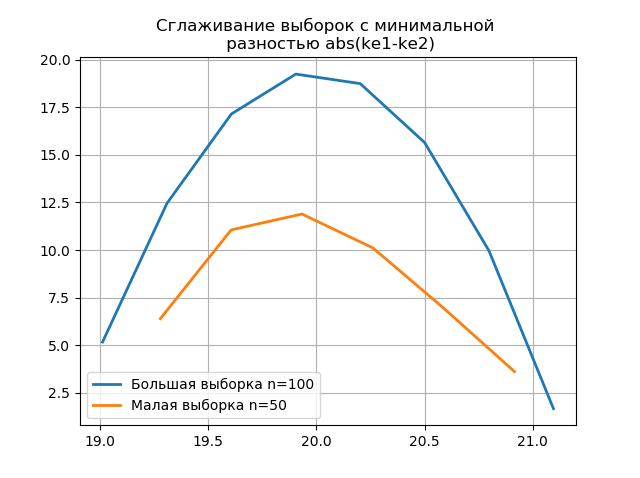
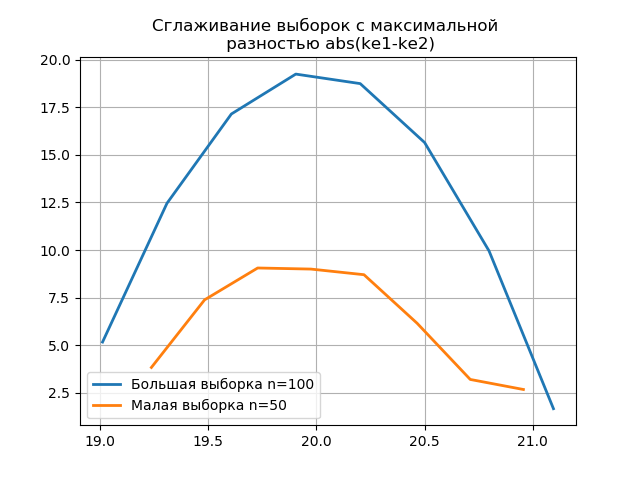
يشير ظهور قفزات إضافية في عينة صغيرة على الرسم البياني لمدرج تكراري سلس مقارنةً بالرسالة السابقة بالإضافة إلى الاختيار الصحيح لمثقف سكوت .

النتائج

أكدت الحسابات الواردة في المقالة في نطاق العينات الصغيرة الشائعة في الإنتاج كفاءة استخدام معامل الانتروبي كمعيار للحفاظ على محتوى المعلومات للعينة مع تقليل حجمها . تعتبر تقنية استخدام أحدث إصدار من وحدة numpy.histogram مع مقيمين مدمجين - "تلقائي" ، "fd" ، "doane" ، "scott" ، "stone" ، "rice" ، "sturges" ، "sqrt" ، وهي كافية تمامًا للتحسين تحليل البيانات التجريبية على تقديرات الفاصل.

المراجع:

1. Hald A. الإحصاء الرياضي مع التطبيقات التقنية. - موسكو: دار النشر. مضاءة ، 1956
2. كالميكوف في ، أنتونيوك إف ، زينكين إن.
تحديد العدد الأمثل لفئات تجميع البيانات التجريبية لتقديرات الفواصل // نشرة جنوب سيبيريا العلمية - 2014. - رقم 3. - P. 56-58.
3. Novitsky P. V. مفهوم القيمة الإنتروبيا للخطأ // تقنية القياس - 1966. - رقم 7. —S. 11-14.
4.numpy.histogram - دليل NumPy v1.16

انخفاض في حجم عينة من البيانات التجريبية دون فقدان المعلومات

ما هي مشكلة الرسوم البيانية البيانات التجريبية

اختيار معايير لتقييم جودة الرسم البياني للبيانات التجريبية

خوارزمية لتقييم جودة الرسم البياني للبيانات التجريبية باستخدام معامل الانتروبيا ووحدة الرسم البياني numpy.histogram

استخدام مكافحة التعرج للتحليل المقارن للرسم البياني

النتائج

المراجع:

More articles: