مقدمة

كيف يمكن معرفة أن الشخص يفهم ماهية الأحاديات؟ هو نفسه سيخبرك بهذا في الدقائق الخمس الأولى من التواصل وسيحاول بالتأكيد شرح ذلك. سوف يكتب أيضًا نصًا حول هذا الموضوع ، وإذا أمكن ، ينشره في مكان ما ، حتى يفهم الآخرون أيضًا ماهية الأحاديات.

بين المبرمجين الوظيفيين ، وخاصة على Haskell ، أصبحت monads قليلاً من ميمي المحلية. وغالبًا ما يحاولون التوضيح ، بدءًا من الحالات الخاصة وإعطاء أمثلة على الاستخدام على الفور. لهذا السبب ، قد لا يدرك المستمع الجوهر الرئيسي للمفهوم ، وستظل الأحجار السحرية سوداء ، أو ببساطة ، أو وسيلة لسحق الآثار الجانبية بلغات وظيفية بحتة.

سأتحدث أولاً عن المفاهيم الأساسية لنظرية الفئة ، ومن ثم من الناحية العملية ، سنتناول تعريف الأحادي ونرى أنه في الواقع ، يستخدم الكثير من المبرمجين هذا التجريد القوي في أحد مظاهره.

يعتمد عرضي التقديمي إلى حد كبير على كتاب Bartosz Milewski بعنوان "نظرية الفئة للمبرمجين" ، الذي تم إنشاؤه كسلسلة من منشورات المدونات ، وهو متوفر في PDF ، وقد تم نشره مؤخرًا في شكل ورقي.

يتم توفير الأمثلة في Haskell ، من المفترض أن يكون القارئ معتادًا على بناء الجملة والمفاهيم الأساسية للغة. في الكتاب المذكور هناك أمثلة في C ++ ، يمكنك مقارنة نقاء وشفافية الكود.

فئة

تعريف

الفئات نفسها هي المنشآت بسيطة جدا. الفئة هي مجموعة من الأشياء والتشكيلات بينها. يمكن اعتبار الأشكال الشكلية أسهم أحادية الاتجاه تربط الكائنات. في الحالة العامة ، لا يوجد شيء معروف عن جوهر الأشياء نفسها. نظرية الفئة لا تعمل مع الكائنات ، ولكن مع الأشكال ، أو بالأحرى ، مع تكوينها .

يتم استخدام الترميز التالي:

• Ob _C - كائنات الفئة C ؛
• Hom _C (A، B) - أشكال من A إلى B ؛
• g ∘ f هي تركيبة التشكل f و g.

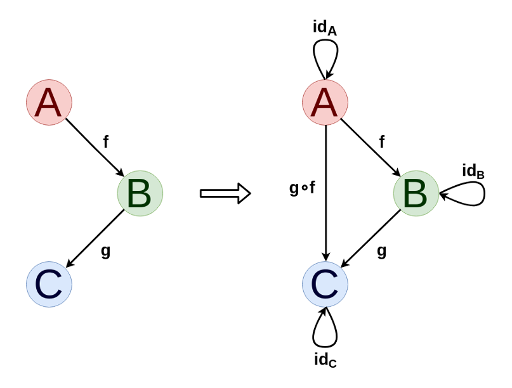
في تعريف الفئة ، تخضع أشكال التشكل لقيود إضافية:

1. بالنسبة لزوج من الأشكال f و g ، إذا كانت f عبارة عن شكل من A إلى B (f ∈ Hom (A ، B)) ، g عبارة عن مورف من B إلى C (g ∈ Hom (B، C)) ، فهناك تركيبة g ∘ f عبارة عن شكل مورفلي من A إلى C (g ∘ f ∈ Hom (A، C)).
2. لكل كائن ، يتم إعطاء معرف هوية الهوية _A ∈ Hom (A، A).

هناك نوعان من الخصائص المهمة التي يجب أن تفي بها أي فئة (بديهيات نظرية الفئة):

1. ترابط التكوين: h ∘ (g ∘ f) = (h ∘ g) ∘ f؛
2. التأليف مع مورف الهوية: إذا كان f ∈ Hom (A، B) ، ثم f ∘ id _A = id _B ∘ f = f.

يتم تصور الفئات بسهولة وبشكل طبيعي كرسوم بيانية موجهة. من حيث المبدأ ، يمكن تمديد أي رسم بياني موجه إلى فئة من خلال إضافة تركيبات من الأشكال والأشكال المتطابقة ، إذا لزم الأمر.

بالنسبة لأي فئة ، يمكنك تحديد فئة مزدوجة (يتم الإشارة إليها بواسطة C ^op ، والتي يتم فيها الحصول على أشكال من خلال تحويل أسهم الفئة الأصلية ، وتكون الكائنات هي نفسها ، وهذا يسمح لنا بصياغة عبارات ونظريات مزدوجة ، لا تتغير حقيقة الأمر عند عكس الأسهم.

لا تشكل الكائنات والتشكل بالضرورة مجموعات (بالمعنى الكلاسيكي ، من نظرية المجموعة) ، لذلك ، في الحالة العامة ، يتم استخدام عبارة "فئة الكائنات". الفئات التي لا تزال فئات الكائنات والأشكال فيها تسمى فئات صغيرة . كذلك سوف نعمل فقط معهم.

أنواع ووظائف

, Haskell, — . , Int Bool — , Int -> Bool — .

id, :

id :: a -> a
id x = x

— , Haskell :

f :: a -> b
g :: b -> c
g . f :: a -> c
(g . f) x = g (f x)

, , — , Set. , — , : . bottom, _|_. , , , bottom. Haskell, , Hask. , Set. , , : Hom_C(A, B) ∈ C. , a -> b — Haskell.

.

Void, ( ). absurd, , , Void, :

absurd :: Void -> a

Unit, — , (). unit , :

unit :: a -> Unit
unit _ = ()

— Bool:

data Bool = True | False

, Void, Unit Bool.

Void , absurd, Bool, Unit. , Void, , .

Bool -> Unit , unit, . Unit -> Bool . (), True, False. , Unit Bool:

true, false :: a -> Bool
true _ = True
false _ = False

Bool Bool — , 4 ( n — 2²ⁿ): id, true false, , not:

not :: Bool -> Bool
not True = False
not False = True

, :

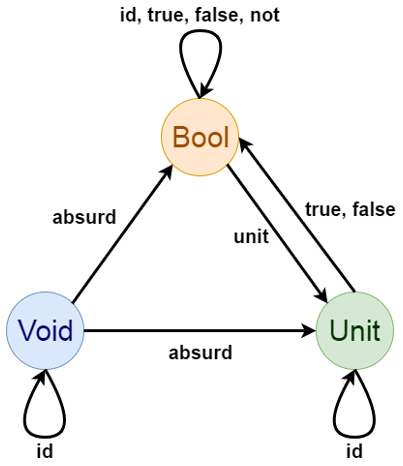
Haskell- .

— . , C D, F . -, C D. a — C, F a — D, . -, : f :: a -> b C F f :: F a -> F b D.

, " " :

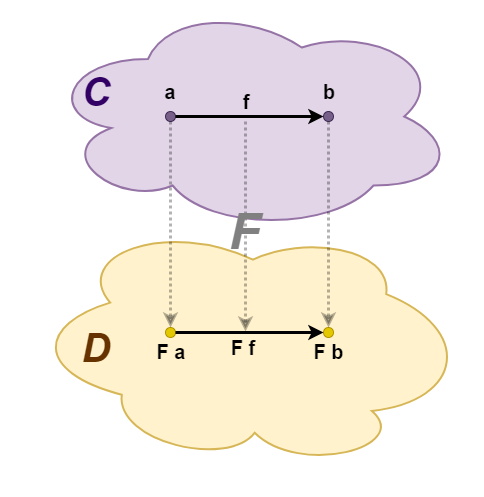
1. h = g ∘ f, F h = F g ∘ F f.
2. id_a — a, F id_a = id_{F a} — F a.

, "" : , , . , , () . , .

. , F :: C -> D G :: D -> E G . F :: C -> E. , , , , . Id_C, Id_D Id_E. , , .

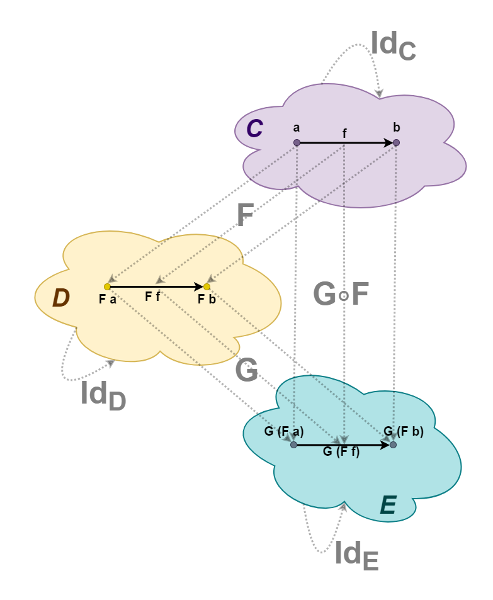
, , -, — (). , Cat ( ).

Haskell . , , - , .

Maybe , a Maybe a ( Maybe !):

data Maybe a = Nothing | Just a

, f :: a -> b F f :: Maybe a -> Maybe b. fmap. , ( ):

--          f                F f
--      /------\    /------------------\
fmap :: (a -> b) -> (Maybe a -> Maybe b)
fmap _ Nothing = Nothing
fmap f (Just x) = Just (f x)

, Maybe — . , , Functor. fmap, , ( — ):

class Functor f where
  fmap :: (a -> b) -> f a -> f b

— , , fmap . f a -> f b, , .

, , , .. , . : , - .

. , . , , — Haskell.

: upCase, , toWords, . toUpper words:

upCase :: String -> String
upCase = map toUpper

toWords :: String -> [String]
toWords = words

:

processString :: String -> [String]
processString = toWords . upCase

, . , processString "upCase toWords".

— , . -, , , -, , .

, a , .

newtype Writer a = Writer (a, String)

, Writer — , fmap:

instance Functor Writer where
  fmap f (Writer (x, s)) = Writer (f x, s)

upCase toWords , , "" Writer:

upCase :: String -> Writer String
upCase s = Writer (map toUpper s, "upCase ")

toWords :: String -> Writer [String]
toWords s = Writer (words s, "toWords ")

, , - . , b , , c c , :

compose :: (a -> Writer b) -> (b -> Writer c) -> (a -> Writer c)
compose f g = \x -> let Writer (y, s1) = f x
                        Writer (z, s2) = g y
                    in Writer (z, s1 ++ s2)

processString :

processString :: String -> [String]
processString = compose upCase toWords

. () a -> b a -> Writer b , a b. , .. a -> Writer a:

writerId :: a -> Writer a
writerId x = Writer (x, "")

, , Hask. , a b a -> b, a -> m b, .. "" - m. (embellished). m, Writer — .

C m. K, , C, .. Ob_K = Ob_C. a -> b K a -> m b C: Hom_K(a, b) = Hom_C(a, m b). , , K — C.

, , , . , m — . Haskell ( Hask):

class Monad m where
  --    
  (>=>)  :: (a -> m b) -> (b -> m c) -> (a -> m c)
  --  
  return :: a -> m a

>=>, "fish", : . , , — , , , . Writer — , compose — >=>, writerId — return.

>=> . , -. a, f, , , bind:

f >=> g = \a -> let mb = f a
                in (bind mb g)
  where
    bind :: m b -> (b -> m c) -> m c

bind b " " m , b m c. >=>. : m b -> (b -> m c) -> m c. , . "" Haskell >>=, bind, return:

class Monad m where
  (>>=)  :: m a -> (a -> m b) -> m b
  return :: a -> m a

, - b -> m c b, m b. , m, fmap, (a -> m b) -> m a -> m (m b). >>= m (m b) m b, "" , . join:

ma >>= g = join (fmap g ma)
  where
    join :: m (m a) -> m a

, Writer :

join :: Writer (Writer a) -> Writer a
join (Writer ((Writer (x, s2)), s1)) = Writer (x, s1 ++ s2)

Monad:

class Functor m => Monad m where
  join   :: m (m a) -> m a
  return :: a -> m a

, m . , fmap >>=:

fmap :: (a -> b) -> m a -> m b
fmap f ma = ma >>= (\a -> return (f a))

, "" .

(.. , ) .

(a -> [b]) -> (b -> [c]) -> (a -> [c]). :

(>=>) :: (a -> [b]) -> (b -> [c]) -> (a -> [c])
f >=> g = \x -> concat (map g (f x))

. a, , — f [b]. , b — g : map g (f x) :: [[c]]. , .

>>= :

(>>=) :: [a] -> (a -> [b]) -> [b]
xs >>= f = concat (map f xs)

return :: a -> [a]. :

return :: a -> [a]
return x = [x]

Monad:

instance Monad [] where
  xs >>= f = concat (map f xs)
  return x = [x]

, . , , . , — , ..

, , - .

, , Maybe. Just, — Nothing. , , :

(>=>) :: (a -> Maybe b) -> (b -> Maybe c) -> (a -> Maybe c)
f >=> g = \x -> case f x of
                  Just y  -> g y
                  Nothing -> Nothing

Monad Maybe:

instance Monad Maybe where
  (Just x) >>= f = f x
  Nothing  >>= f = Nothing
  return x = Just x

, . , - , , - . Either String a, : , . :

data Either a b = Left a | Right b

, . . :

type WithException a = Either String a

Maybe:

(>=>) :: (a -> WithException b) -> (b -> WithException c) -> (a -> WithException c)
f >=> g = \x -> case f x of
                  Right y -> g y
                  err     -> err

Monad :

instance Monad WithException where
  (Right x) >>= f = f x
  err >>= f = err
  return x = Right x

, , write-only , . a -> b , , . , , ( , ):

a -> s -> (b, s)

:

newtype State s a = State (s -> (a, s))

s , State s . runState:

runState :: State s a -> s -> (a, s)
runState (State f) s = f s

Functor:

instance Functor (State s) where
  fmap f state = State st'
    where
     st' prevState = let (a, newState) = runState state prevState
                     in (f a, newState)

, a b, , a -> State s b, State s — . , :

(>=>) :: (a -> State s b) -> (b -> State s c) -> (a -> State s c)
f >=> g = \x -> State (\s -> let (y, s') = runState (f x) s
                             in runState (g y) s')

Monad. , return, , -:

instance Monad (State s) where
  stateA >>= f = State (\s -> let (a, s') = runState stateA s
                              in runState (f a) s')
  return a = State (\s -> (a, s))

, . , Unit s , Unit -> State s s:

get :: Unit -> State s s
get _ = State (\s -> (s, s))

, Unit . , .

, , . , , , s Unit, s -> State s Unit:

put :: s -> State s Unit
put s = State (\_ -> ((), s))

, , /. , " " RealWorld, . RealWorld - , (, ). :

type IO a = State RealWorld a

IO — , Haskell, "". , . , , , -, .