🕦 👲🏿 👩‍👧 حالات الكم العصبية - تمثيل دالة موجية بواسطة شبكة عصبية 🌄 👐🏽 🚶🏻

في هذه المقالة ، سننظر في التطبيق غير المعتاد للشبكات العصبية بشكل عام وآلات بولتزمان المحدودة بشكل خاص لحل مشكلتين معقدتين هما ميكانيكا الكم - إيجاد طاقة الحالة الأساسية وتقريب وظيفة الموجة لنظام كثير من الجسم.

يمكننا القول أن هذه عبارة عن إعادة سرد مجانية ومبسطة لمقال [2] ، نُشر في مجلة Science في عام 2017 وبعض الأعمال اللاحقة. لم أجد معارضًا علمية مشهورة لهذا العمل باللغة الروسية ( وهذا فقط أحد الإصدارات الإنجليزية) ، على الرغم من أنه بدا لي مثيراً للاهتمام.

الحد الأدنى من المفاهيم الأساسية من ميكانيكا الكم والتعلم العميق

أريد أن أشير على الفور إلى أن هذه التعريفات مبسطة للغاية . أحضر لهم لأولئك الذين المشكلة الموصوفة هي غابة مظلمة.

الحالة هي ببساطة مجموعة من الكميات المادية التي تصف النظام. على سبيل المثال ، بالنسبة للإلكترون الذي يطير في الفضاء ، فإنه سيكون إحداثياته وزخمه ، وبالنسبة للشبكة البلورية ، ستكون مجموعة من ذرات الذرات الموجودة في العقد.

وظيفة الموجة للنظام هي وظيفة معقدة لحالة النظام. مربع أسود معين يأخذ إدخالًا ، على سبيل المثال ، مجموعة من الدورات ، لكنه يُرجع رقمًا معقدًا. الخاصية الرئيسية لوظيفة الموجة المهمة بالنسبة لنا هي أن مربعها يساوي احتمال هذه الحالة:

P s i (s) P s i (s)^{*} = P (s)

$\ Psi (s) \ Psi (s) ^ * = P (s)$

من المنطقي أن تطبيع مربع الدالة الموجية إلى الوحدة (وهذه أيضًا واحدة من المشكلات المهمة).

مساحة هيلبرت - في حالتنا ، مثل هذا التعريف يكفي - مساحة جميع الحالات المحتملة للنظام. على سبيل المثال ، بالنسبة لنظام من 40 يدور يمكن أن تأخذ القيم +1 أو -1 ، مساحة Hilbert هي كل شيء

2^{40}

$2 ^ {40}$ الظروف الممكنة. للإحداثيات التي يمكن أن تأخذ القيم

[- i n f t y ، + i n f t y]

$[- \ infty ، + \ infty]$ ، البعد من الفضاء هيلبرت هو لانهائي. إنه البعد الهائل لمساحة Hilbert لأي أنظمة حقيقية تمثل المشكلة الرئيسية التي لا تسمح بحل المعادلات تحليليًا: في هذه العملية سيكون هناك تكامل / ملخصات على كامل مساحة Hilbert التي لا يمكن حسابها "بشكل مباشر". حقيقة غريبة: طوال حياة الكون ، لا يمكنك مقابلة سوى جزء صغير من جميع الحالات الممكنة المدرجة في مساحة هيلبرت. يتضح ذلك جيدًا من خلال صورة من مقال حول Tensor Networks [1] ، والتي تصور بشكل تخطيطي كامل مساحة Hilbert وتلك الحالات التي يمكن تلبيتها بعد كثير الحدود من خاصية تعقيد الفضاء (عدد الأجسام والجزيئات والدوران ، إلخ)

آلة بولتزمان محدودة - إذا كان من الصعب شرحها ، فهي نموذج احتمالي غير مباشر ، حيث يكمن القيد في الاستقلال الشرطي لاحتمالات عقد طبقة واحدة من عقد الطبقة نفسها. إذا كان ذلك بطريقة بسيطة ، فهذه شبكة عصبية ذات مدخل وطبقة واحدة مخفية. يمكن أن تكون قيم مخرجات الخلايا العصبية في الطبقة المخفية 0 أو 1. والفرق من الشبكة العصبية المعتادة هو أن مخرجات الخلايا العصبية المخفية هي متغيرات عشوائية تم اختيارها باحتمال يساوي قيمة وظيفة التنشيط:

P_{i} (1) = s i g m a (b_{i} + s u m_{j} W_{i j} s_{j})

$P_i (1) = \ sigma (b_i + \ sum_jW_ {ij} s_j)$

حيث

س ي ج م ا

$\ سيجما$ - وظيفة التنشيط السيني ،

b_{i}

$b_i$ - إزاحة للخلية العصبية الأولى ،

W

$W$ - وزن الشبكة العصبية ،

s_{j}

$s_j$ - طبقة مرئية. تنتمي ماكينات Boltzmann المحدودة إلى ما يسمى "نماذج الطاقة" ، حيث يمكننا التعبير عن احتمال وجود حالة معينة من الجهاز باستخدام طاقة هذا الجهاز:

E (v ، h) = - a^{T} v - b^{T} h - v^{T} W h

$E (v، h) = -a ^ Tv - b ^ Th - v ^ TWh$

حيث v و h هما الطبقات المرئية والمخفية ، a و b هما إزاحة الطبقات المرئية والمخفية ، W هما الأوزان. ثم احتمال الدولة هو في الشكل:

P (v ، h) = f r a c 1 Z e^{- E (v ، h)}

$P (v، h) = \ frac {1} {Z} e ^ {- E (v، h)}$

حيث Z هو مصطلح التطبيع ، ويسمى أيضًا المجموع الإحصائي (من الضروري أن يكون الاحتمال الكلي مساوياً للوحدة).

مقدمة

اليوم ، هناك رأي بين المتخصصين في التعلم العميق الذي محدود
آلات بولتزمان (المشار إليها فيما يلي - OMB) هي مفهوم قديم لا ينطبق عمليا في المهام الحقيقية. ومع ذلك ، في عام 2017 ، ظهر مقال في مجلة ساينس Science والذي أظهر الاستخدام الفعال للغاية لـ OMB في مشاكل ميكانيكا الكم.

لاحظ المؤلفون حقيقتين مهمتين قد تبدو واضحة ، لكنهما لم يسبق لأحد أن حدث:

OMB هي شبكة عصبية ، وفقًا لنظرية Tsybenko العالمية ، يمكنها نظريًا تقريبًا أي وظيفة بدقة عالية بشكل تعسفي (لا يزال هناك الكثير من القيود ، لكن يمكنك تخطيها).
OMB هو نظام يكون احتمال كل حالة هو وظيفة الإدخال (الطبقة المرئية) والأوزان والتشريد في الشبكة العصبية.

قال المؤلفان: حسناً ، دعنا نوصِّف نظامنا تمامًا بوظيفة الموجة ، التي هي جذر طاقة OMB ، ومدخلات OMB هي خصائص حالة النظام لدينا (الإحداثيات ، الدورات ، إلخ):

P s i (s) = f r a c 1 Z s q r t e^{E (s ، h)}

$\ Psi (s) = \ frac {1} {Z} \ sqrt {e ^ {E (s، h)}}$

حيث s هي خصائص الحالة (على سبيل المثال ، ظهور) ، h هي مخرجات الطبقة المخفية من OMB ، E هي طاقة OMB ، Z هي ثابت التطبيع (المجموع الإحصائي).

هذا كل شيء ، المقالة في العلوم جاهزة ، ثم تبقى بعض التفاصيل الصغيرة. على سبيل المثال ، من الضروري حل مشكلة وظيفة التقسيم غير القابلة للحساب بسبب الحجم الهائل لمساحة Hilbert. تخبرنا نظرية Tsybenko أن الشبكة العصبية يمكنها تقريب أي وظيفة ، لكنها لا توضح على الإطلاق كيفية العثور على مجموعة مناسبة من الأوزان والإزاحات لهذا الغرض. حسنًا ، وكالعادة ، تبدأ المتعة هنا.

التدريب النموذجي

يوجد الآن عدد قليل من التعديلات على النهج الأصلي ، لكنني لن أفكر إلا في مقاربة المقال الأصلي [2].

مهمة

في حالتنا ، ستكون مهمة التدريب كالتالي: لإيجاد تقريب لوظيفة الموجة التي من شأنها أن تجعل الحالة ذات الطاقة الدنيا هي الأكثر احتمالًا. هذا واضح بشكل حدسي: وظيفة الموجة تعطينا احتمالية الحالة ، أو القيمة الذاتية لـ Hamiltonian (مشغل الطاقة ، أو حتى الطاقة الأكثر بساطة - في إطار هذه المقالة ، يكون هذا الفهم كافياً) لأن وظيفة الموجة هي الطاقة. كل شيء بسيط.

في الواقع ، سوف نسعى جاهدين لتحسين كمية أخرى ، ما يسمى الطاقة المحلية ، والتي تكون دائمًا أكبر من أو تساوي طاقة الحالة الأساسية:

E_{l o c} (s i g m a) = R e s u m_{s i g m a s i g m a^{'}} H_{s i g m a s i g m a^{'}} f r a c P s i (s i g m a^{'}) P s i (s i g m a)

$E_ {loc} (\ sigma) = Re \ sum _ {\ sigma \ sigma '} H _ {\ sigma \ sigma'} \ frac {\ Psi (\ sigma ')} {\ Psi (\ sigma)}$

هنا

س ي ج م ا

$\ سيجما$ هي حالتنا

س ي ج م ا^{'}

$\ سيجما '$ - جميع الحالات الممكنة للفضاء هيلبرت (في الواقع سننظر في قيمة أكثر تقريبية) ،

H_{s i g m a s i g m a^{'}}

$H _ {\ sigma \ sigma '}$ هو عنصر المصفوفة من هاميلتون. هذا يعتمد بشكل كبير على هاميلتون ، على سبيل المثال ، بالنسبة لنموذج Ising

f (s i g m a)

$f (\ sigma)$ إذا

s i g m a = s i g m a^{'}

$\ sigma = \ sigma '$ و

- c o n s t

$-const$ في جميع الحالات الأخرى. لا تتوقف هنا الآن ؛ من المهم أن توجد هذه العناصر للعديد من سكان هاميلتون.

عملية التحسين

أخذ العينات

جزء مهم من مقاربة المقال الأصلي كان عملية أخذ العينات. تم استخدام صيغة معدلة من خوارزمية متروبوليس هاستينغز . خلاصة القول هي:

نبدأ من حالة عشوائية.
نقوم بتغيير علامة تدور تم اختيارها عشوائيًا إلى الاتجاه المعاكس (للإحداثيات ، هناك تعديلات أخرى ، ولكنها موجودة أيضًا).
مع الاحتمال يساوي $P (\ sigma '| \ sigma) = \ Big | {\ frac {\ Psi (\ sigma')} {\ Psi (\ sigma)} \ Big | ^ 2$ ، الانتقال إلى حالة جديدة.
كرر مرات N.

نتيجة لذلك ، نحصل على مجموعة من الحالات العشوائية المحددة وفقًا للتوزيع الذي تعطينا دالة الموجة لدينا. يمكنك حساب قيم الطاقة في كل ولاية والتوقع الرياضي للطاقة

m a t h b b E (E_{l o c})

$\ mathbb {E} (E_ {loc})$ .

يمكن إثبات أن تقدير تدرج الطاقة (بشكل أدق ، القيمة المتوقعة للهاميلتون) يساوي:

G_{k} (x) = 2 * (E_{l o c} (x) - m a t h b b E (E_{l o c})) * D_{k}^{*} (x)

$G_k (x) = 2 * (E_ {loc} (x) - \ mathbb {E} (E_ {loc})) * D ^ * _ k (x)$

استنتاج

هذا من محاضرة ألقاها ج. كارلو في عام 2017 للمدرسة المتقدمة حول علوم الكم وتكنولوجيا الكم. هناك مداخل على يوتيوب.

دلالة:

D_{k}^{*} (x) = f r a c ج ز ئ ي_{p_{k}} P s i (x) P s i (x)

$D ^ * _ k (x) = \ frac {\ جزئي_ {p_k} \ Psi (x)} {\ Psi (x)}$

ثم:

\ جزئية {{p_k} \ mathbb {E} (H) =

$\ جزئية {{p_k} \ mathbb {E} (H) =$

ج ز ئ ي ة f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} =

$\ جزئية \ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} =$

f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} D_{k} (x^{'}) P s i (x^{'}) s u m_{x} | P s i (x) |^{2} + f r a c s u m_{x x^{'}} P s i^{*} (x) D_{k}^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} -

$\ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} D_k (x ') \ Psi (x')} {\ sum_x | \ Psi (x) | ^ 2} + \ frac {\ sum_ {xx '} \ Psi ^ * (x) D_k ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} -$

f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} f r a c s u m_{x} | P s i (x) |^{2} (D_{k} (x) - D_{k}^{*} (x)) s u m_{x} | P s i (x) |^{2} =

$\ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} \ frac {\ sum_x | \ Psi (x) | ^ 2 (D_k (x) - D ^ * _ k (x))} {\ sum_x | \ Psi (x) | ^ 2} =$

f r a c s u m_{x x^{'}} f r a c P s i^{*} (x) P s i^{*} (x^{'}) H_{x x^{'}} D_{k} (x^{'}) | P s i (x^{'}) |^{2} + s u m_{x x^{'}} | P s i (x) |^{2} H_{x x^{'}} D_{k}^{*} (x^{'}) f r a c P s i (x^{'}) P s i (x) s u m_{x} | P s i (x) |^{2} -

$\ frac {\ sum_ {xx '} \ frac {\ Psi ^ * (x)} {\ Psi ^ * (x')} H_ {xx '} D_k (x') | \ Psi (x ') | ^ 2 + \ sum_ {xx '} | \ Psi (x) | ^ 2H_ {xx'} D ^ * _ k (x ') \ frac {\ Psi (x')} {\ Psi (x)}} {\ sum_x | \ Psi (x) | ^ 2} -$

m a t h b b E (H) f r a c s u m_{x} | P s i (x) |^{2} (D_{k} (x) + D^{*} * k (x)) s u m_{x} | P s i (x) |^{2} ت ق ر ي ب ا د و ل ا

$\ mathbb {E} (H) \ frac {\ sum_x | \ Psi (x) | ^ 2 (D_k (x) + D ^ * * k (x))} {\ sum_x | \ Psi (x) | ^ 2 } \ تقريبا دولا$

m a t h b b E (E_{l o c} D_{k}^{*}) - m a t h b b E (E_{l o c}) m a t h b b E (D_{k}^{*}) + C

$\ mathbb {E} (E_ {loc} D ^ * _ k) - \ mathbb {E} (E_ {loc}) \ mathbb {E} (D ^ * _ k) + C$

ثم نحل مشكلة التحسين:

نحن الدول عينة من OMB لدينا.
نحسب طاقة كل ولاية.
تقدير التدرج.
نقوم بتحديث وزن OMB.

نتيجة لذلك ، يميل التدرج اللوني للطاقة إلى الصفر ، وتنخفض قيمة الطاقة ، كما ينخفض عدد الحالات الجديدة الفريدة في عملية Metropolis-Hastings ، لأنه من خلال أخذ العينات من دالة الموجة الحقيقية ، سنحصل دائمًا على الحالة الأرضية. حدسي ، وهذا يبدو منطقيا.

في العمل الأصلي ، بالنسبة للأنظمة الصغيرة ، تم الحصول على قيم طاقة الحالة الأرضية ، وهي قريبة جدًا من القيم الدقيقة التي تم الحصول عليها تحليليًا. تم إجراء مقارنة مع الأساليب المعروفة لإيجاد طاقة الأرض الأساسية ، وفاز NQS ، خاصة بالنظر إلى التعقيد الحسابي المنخفض نسبياً لـ NQS مقارنةً بالطرق المعروفة.

NetKet - مكتبة من نهج "المخترعين"

قام أحد مؤلفي المقال الأصلي [2] مع فريقه بتطوير مكتبة NetKet الممتازة [3] ، التي تحتوي على C-kernel محسنة جدًا (في رأيي) ، بالإضافة إلى API Python ، التي تعمل مع التجريدات عالية المستوى.

يمكن تثبيت المكتبة عبر النقطة. سيتعين على مستخدمي Windows 10 استخدام نظام Linux الفرعي لنظام Windows.

دعنا نفكر في العمل مع المكتبة كمثال لسلسلة من 40 يدور مع القيم + -1 / 2. سننظر في نموذج هايزنبرغ ، الذي يأخذ في الاعتبار التفاعلات المجاورة.

يحتوي NetKet على وثائق ممتازة تتيح لك معرفة ما يجب القيام به وكيفية القيام به بسرعة. هناك العديد من الطرز المدمجة (ظهور ، بوزونات ، إيسينغ ، نماذج هيزنبرغ ، إلخ) ، والقدرة على وصف النموذج تمامًا بنفسك.

وصف العد

يتم عرض جميع النماذج في الرسوم البيانية. بالنسبة إلى سلسلتنا ، فإن طراز Hypercube المدمج ذي البعد الواحد وشروط الحدود الدورية مناسب:

import netket as nk graph = nk.graph.Hypercube(length=40, n_dim=1, pbc=True)

وصف هيلبرت الفضاء

إن مساحة Hilbert لدينا بسيطة للغاية - يمكن أن تدور جميع أشكال الدوران إما +1 / أو -1/2. في هذه الحالة ، يكون النموذج المضمن للدوران مناسبًا:

 hilbert = nk.hilbert.Spin(graph=graph, s=0.5)

وصف هاميلتون

كما كتبت بالفعل ، في حالتنا ، فإن Hamiltonian هو Heisenberg Hamiltonian حيث يوجد مشغل مدمج:

 hamiltonian = nk.operator.Heisenberg(hilbert=hilbert)

وصف الإدارة القائمة على النتائج

في NetKet ، يمكنك استخدام تطبيق RBM جاهز للدوران - هذه هي حالتنا فقط. ولكن بشكل عام هناك العديد من السيارات ، يمكنك تجربة سيارات مختلفة.

 nk.machine.RbmSpin(hilbert=hilbert, alpha=4) machine.init_random_parameters(seed=42, sigma=0.01)

هنا ألفا هي كثافة الخلايا العصبية في الطبقة المخفية. بالنسبة لـ 40 خلية عصبية مرئية و ألفا 4 ، سيكون هناك 160 منهم ، وهناك طريقة أخرى للإشارة مباشرة بالرقم. الأمر الثاني تهيئة الأوزان بشكل عشوائي من

N (0 ، s i g m a)

$N (0 ، \ sigma)$ . في حالتنا ، سيغما هي 0.01.

زملر

العينات هي كائن سيتم إرجاعه إلينا بواسطة عينة من توزيعنا ، والتي يتم الحصول عليها بواسطة دالة الموج على مساحة Hilbert. سنستخدم خوارزمية متروبوليس هاستينغز الموضحة أعلاه ، المعدلة لمهمتنا:

 sampler = nk.sampler.MetropolisExchangePt( machine=machine, graph=graph, d_max=1, n_replicas=12 )

لكي نكون دقيقين ، فإن العينات هي خوارزمية أصعب من تلك الموضحة أعلاه. هنا نتحقق في الوقت نفسه من أكثر من 12 خيارًا بالتوازي لتحديد النقطة التالية. لكن المبدأ ، بشكل عام ، هو نفسه.

محسن

يصف هذا المحسن الذي سيتم استخدامه لتحديث أوزان النموذج. وفقًا للتجربة الشخصية في العمل مع الشبكات العصبية في المناطق الأكثر "دراية" بها ، فإن الخيار الأفضل والأكثر موثوقية هو النسب التدرج العشوائي القديم الجيد مع لحظة (موصوفة جيدًا هنا ):

 opt = nk.optimizer.Momentum(learning_rate=1e-2, beta=0.9)

تدريب

يتلقى NetKet تدريباً بدون مدرس (حالتنا) ومع مدرس (على سبيل المثال ، ما يسمى "التصوير المقطعي الكمومي" ، ولكن هذا موضوع مقالة منفصلة). نحن ببساطة نصف "المعلمين" ، وهذا هو:

 vc = nk.variational.Vmc( hamiltonian=hamiltonian, sampler=sampler, optimizer=opt, n_samples=1000, use_iterative=True )

يشير مونت كارلو المتغير إلى كيف نقيم تدرج الوظيفة التي نحسنها. n_smaples هو حجم العينة من التوزيع الذي n_smaples العينات.

النتائج

سنقوم بتشغيل النموذج على النحو التالي:

 vc.run(output_prefix=output, n_iter=1000, save_params_every=10)

تم إنشاء المكتبة باستخدام OpenMPI ، وسيحتاج البرنامج النصي إلى تشغيل مثل هذا: mpirun -n 12 python Main.py (12 هو عدد النوى).

النتائج التي تلقيتها هي كما يلي:

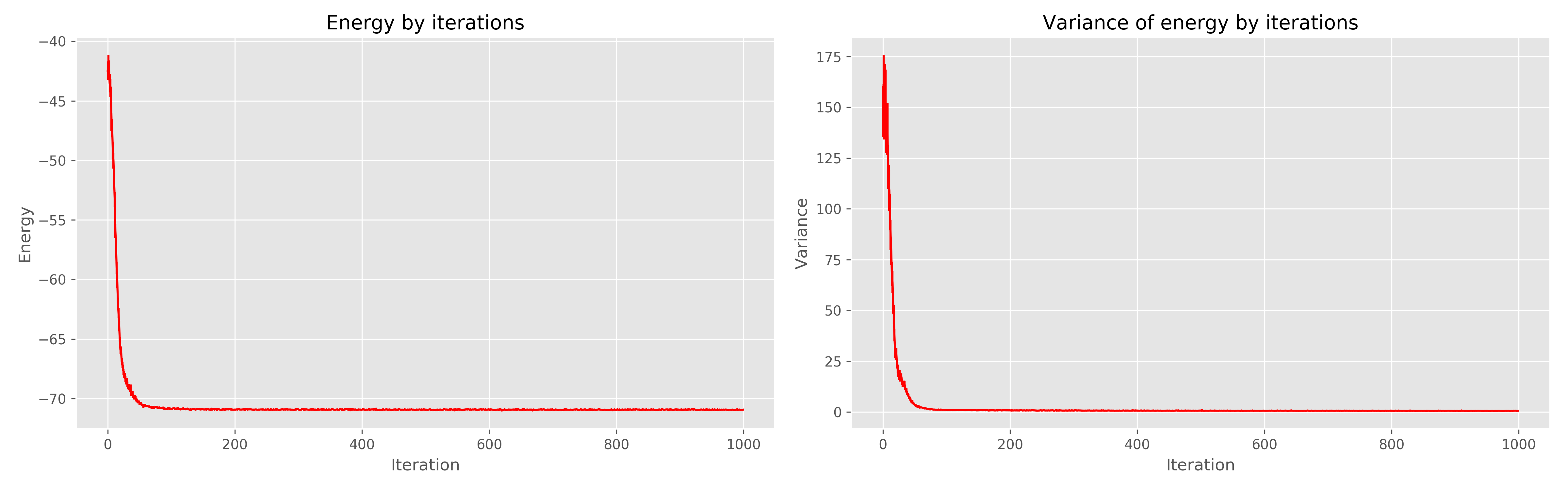
على اليسار هو رسم بياني للطاقة من عصر التعلم ، على اليمين هو تشتت الطاقة من عصر التعلم.
يمكن أن نرى أن 1000 عصر من الواضح أنها زائدة عن الحاجة ، وأن 300 منها كانت كافية ، بشكل عام ، تعمل بشكل رائع للغاية ، وتتقارب بسرعة.

أدب

Orús R. مقدمة عملية لشبكات التينسور: حالات منتج Matrix وحالات الزوج المتشابك المتوقعة // Annals of Physics. - 2014. - T. 349. - S. 117-158.
Carleo G.، Troyer M. حل مشكلة الكم في الجسم مع الشبكات العصبية الاصطناعية // العلوم. - 2017. - T. 355. - رقم 6325. - 602-606.
www.netket.org

حالات الكم العصبية - تمثيل دالة موجية بواسطة شبكة عصبية