الحفز الموني من حيث كيمياء الكم. الجزء الثاني: الإلكترونية مقابل الرابطة الكيميائية muon

منغوابف أن كيمياء الكم تفكر في مبدأ تحفيز الميون: كيف بالضبط يخفض الميون درجة حرارة البلازما المرغوبة. في جزأين (الجزء الأول يمكن قراءته هنا ).

جوهر الجزء الثاني بسيط: الميون أثقل من الإلكترون ، لذلك يوفر رابطة كيميائية أقوى ونهج أقرب من النواة ، وبالتالي خفض درجة حرارة البلازما المطلوبة لإشعال التفاعل النووي الحراري.

لكن أولئك الذين يرغبون في إلقاء نظرة على الصيغ ، الرسوم البيانية ، ويرون الجوهر المفاهيمي للكيمياء الكمومية كما هو مطبق على أبسط الجزيئات (شبه) ، مرحبًا بك في قطة.

مقدمة

في الجزء الأول (انظر هنا ) درسنا الفرق بين ذرة الهيدروجين $$$\ mathrm {H} ^ \ cdot = \ mathrm {p ^ + e ^ -}$ من نظيره muon الثقيلة $$$\ mathrm {p} ^ + \ mu ^ -$ : في الحالة الثانية ، سيتم ربط الميون بقوة أكبر ، وسيجلس على مسافة أقرب من البروتون. في الوقت نفسه ، درسنا بعض الأشياء المهمة التي سنحتاجها هنا (أشكال المدارات والنظام الذري للوحدات).

في الجزء الثاني (على سبيل المثال ، هنا) سنحاول أن نفهم لماذا وكيف تنخفض درجة حرارة البلازما المطلوبة لإشعال التفاعل النووي الحراري. ردود الفعل التي تهمنا هي:

$$

$$\ mathrm {{} ^ nH + {} ^ m H \ rightarrow} \ \ text {new kernels + energy}$$

حيث n ، m = 1،2،3 تتوافق مع البروتون ، الديوتيريوم والتريتيوم ، على التوالي. من الطبيعي أن يكون لهذه النوى شحنة موجبة ، لذا إذا حاولت تقريبها ، فستبدأ في صدها وفقًا لقانون كولوم (انظر الجزء السابق ) ، وهذا هو الحاجز الذي يمنع ظهور ردود فعل الاندماج. بالمناسبة ، في حالة تفاعلات الانحلال النووي ، يكون لهذا التنافر دور معاكس ، لأنه بعد الانفصال عن النواة المشتركة ، فإن الشظايا ، الطاردة من بعضها البعض ، تكتسب طاقة حركية إضافية ، وهذه الطاقة هي التي يتم تسخينها في محطات الطاقة النووية.

للتغلب على هذا الحاجز Coulomb ، هناك حاجة إلى زيادة في درجة حرارة البلازما ( T ) ، والتي ، كما يتذكر الجميع من المدرسة من MKT ، يرتبط متوسط ​​سرعة الجسيمات في البلازما ( الخامس ) من الصيغة

$$

$$mv ^ 2 = 3k_ \ mathrm {B} T$$

حيث m هي كتلة الجزيئات ، و $$$k_ \ mathrm {B}$ - بولتزمان ثابت .

ولكن ، دعنا نتخيل أننا قمنا بدمج نوتين هيدروجين في جسيم معين ، حيث يقعان بالفعل بالقرب منه ، وبالتالي فإن بقية الحاجز الخاص بهما صغير جدًا بالفعل. ثم سنحتاج إلى تسريع هذه الجسيمات بشكل كبير (اقرأ: نحتاج إلى درجات حرارة منخفضة) من أجل دمجها في شيء جديد. ومثل هذا الدور يجب أن يلعب أيون وسيط $$$(\ mathrm {{} ^ nH} \ mu ^ - \ mathrm {{} ^ mH}) ^ +$ ، التناظرية من أيون جزيء الهيدروجين $$$\ mathrm {H} _2 ^ + = (\ mathrm {He ^ -H}) ^ +$ .
بعد فحص الاختلافات بين هذين الجسيمين ، سوف ندرك مدى فعالية الميون في خفض درجة حرارة الاشتعال للانصهار النووي الحراري.

الحليب MO LKAO الطريقة

لذلك ، لدينا نظامنا الجزيئي ، الذي يتكون من 2 نواة هيدروجين مع شحنة + e (معامل شحنة إلكترون واحد) وجسيم واحد (إلكترون أو ميون) مع شحنة - ه . نظامنا ، إلى أن يتصادم مع جزيئات أخرى ، معزول ، وبالتالي يمكن أن تتحلل طاقته إلى أجزائه المكونة:

$$

$$E = T (\ mathrm {H} _1) + T (\ mathrm {H} _2) + \ underbrace {T (\ mathrm {e} ^ - / \ mu ^ -) + V (\ mathrm {H_1 \ text {من} H_2}) + V (\ mathrm {\ mathrm {e} ^ - / \ mu ^ - \ text {} \ mathrm {H} _1}) + V (\ mathrm {\ mathrm {e} ^ - / \ mu ^ - \ text {k} \ mathrm {H} _2})} _ {E_ \ mathrm {e}}$$

حيث المصطلحين الأولين ( $$$T (\ mathrm {H} _1)$ و $$$T (\ mathrm {H} _2)$ هي الطاقة الحركية لنواة الهيدروجين ، المصطلح الثالث ( $$$T (\ mathrm {e} ^ - / \ mu ^ -)$ ) هي الطاقة الحركية لجسيم سالب (إلكترون أو ميون) ، المصطلح الرابع $$$V (\ mathrm {H_1 \ text {from} H_2})$ هي طاقة Coulomb صد الهيدروجين من بعضها البعض ، والباقيان هما جذب Coulomb للإلكترون / الميون لكل من البروتونات. في الحالة العامة ، هذه مشكلة ثلاثية الجسم ، مجرد مشكلة كوانتية. بطبيعة الحال ، حلها في الجبهة أمر صعب للغاية. ولكن لحسن الحظ ، فإن النوى أثقل ب 1800 مرة على الأقل من الإلكترون ، و 10 أثقل من الميون ، لذلك سوف تتحرك أبطأ بشكل واضح من الجسيمات السلبية الصغيرة. نتيجةً لذلك ، يمكنك أولاً حل المشكلة بدورها: أولاً ، يمكنك العثور على طاقة الحركات غير المرتبطة بحركة النواة ، أي $$$E_ \ mathrm {e}$ ثم الطاقة الكاملة. يبدو مثل هذا.

1. يتم تحديد ترتيب نوى الهيدروجين بالنسبة لبعضها البعض ، وهذا يحدد التفاعلات Coulomb بينهما وبين الإلكترون / الميون. كولوم المحتملة $$$V (R) = k \ frac {q_1q_2} {R}$ يعتمد فقط على شحنات الجسيمات $$$q_i$ والمسافة بينهما ، لذلك بالنسبة لجميع نظائر الهيدروجين ، ستكون هذه القيمة هي نفسها. علاوة على ذلك ، يتم حل مشكلة حركة الإلكترون / الميون في مجال هذه النوى. هذه هي مهمة جسد واحد.
2. هذه الطاقات $$$E_ \ mathrm {e}$ يتم احتسابها لجميع الترتيبات الممكنة للنواة بالنسبة لبعضها البعض ، وستكون هذه الطاقة الكامنة الفعالة لحركة النواة. في حالتنا ، نحن بحاجة إلى حساب الطاقات على مسافات مختلفة بالنسبة لبعضها البعض ، وبالتالي فإن احتمالية وجود زوج من النوى دائمًا أحادي البعد. حسنًا ، إذن نحن بحاجة فقط إلى حل مشكلة الجسمين المتمثلة في حركة نظيري الهيدروجين بالنسبة لبعضهما البعض.

من الواضح أن جذر المشكلة في حسابنا لطاقة الإلكترون / الميون في مجال النواة $$$E_ \ mathrm {e}$ . في الواقع ، هذا هو الرابط الكيميائي: إمكانية معينة تجمع النواة معًا في أماكن معينة. ومهمة العثور على طاقة الترابط الكيميائي هي المهمة الرئيسية في كيمياء الكم.

لسوء الحظ ، كلا من الميون والإلكترون جزيئات كمومية ، لذلك ، من أجل إيجاد هذه الطاقة ، علينا أن نلجأ إلى أساليب ميكانيكا الكم. في الواقع ، يتم حل مشكلتنا المتمثلة في حركة الإلكترون / الميون في مجال نوتين متطابقتين بشكل صريح (انظر هنا ) ، ولكن هذا الحل معقد للغاية والنتيجة ليست واضحة كما في حالة ذرة تشبه الهيدروجين. لذلك ، سوف نحاول تفكيك نهج تقريبي مختلف ، والذي ينطبق على أي أنظمة. هذا هو ما يسمى طريقة المدارات الجزيئية كمجموعات خطية من المدارات الذرية ، أو MO LKAO.

دعونا نلقي نظرة فاحصة على معادلة شرودنجر لحركة الإلكترون / الميون في مجال نوى الهيدروجين:

$$

$$\ hat {H} \ psi = \ underbrace {\ left (\ overbrace {- \ frac {1} {2m} (\ frac {\ جزئية ^ 2} {\ جزئية x ^ 2} + \ frac {\ جزئية ^ 2} {\ جزئي y ^ 2} + \ frac {\ جزئية ^ 2} {\ جزئية z ^ 2})} ^ {\ hat {T}} + \ overbrace {- \ frac {1} {R_1}} ^ {\ hat {V} _1} + \ overbrace {- \ frac {1} {R_2}} ^ {\ hat {V} _2} + \ overbrace {\ frac {1} {R}} ^ {\ hat {V } _ \ mathrm {HH}} \ right)} _ {\ hat {H}} \ psi = E \ psi$$

تمت كتابة هذه المعادلة في النظام الذري للوحدات (انظر PS في الجزء السابق ) ، وبالتالي ، فإن شحنة نواة الهيدروجين والإلكترون / الميون هي +1 ، - 1 ، على التوالي ، تكون كتلة الإلكترون م = 1 ، وبالنسبة للميون م ≈207.

وإذا ألقيت نظرة فاحصة ، يمكنك أن ترى أنه في منطقة هاميلتون يمكنك اختيار قطعة متصلة بحتة بحركة جسيم سالب حول واحدة فقط من النواة ، والتي هي مجرد هاميلتون لذرة الهيدروجين ، ويمكن القيام بذلك بطريقتين:

$$

$$\ hat {H} = (\ overbrace {\ hat {T} + \ hat {V} _1} ^ {\ hat {H} _ {1}} + \ hat {V} _2 + \ hat {V} _ \ mathrm {HH}) = (\ overbrace {\ hat {T} + \ hat {V} _2} ^ {\ hat {H} _ {2}} + \ hat {V} _1 + \ hat {V} _ \ mathrm {HH})$$

خارج هاميلتون لذرة تشبه الهيدروجين ( $$$\ hat {H} _i ، \ i = 1.2 دولا$ ) لدينا دائمًا قطعتان: طاقة تفاعل الإلكترون / الميون مع نواة أخرى ( $$$\ hat {V} _j$ ) وطرد الطاقة النووية ( $$$\ hat {V} _ \ mathrm {HH}$ ). الثاني منها لا يؤثر على حركة الإلكترونات على الإطلاق - إنه مجرد تحول في الطاقة بمقدار معين ، لكن تفاعل الإلكترون مع نواة أخرى أمر مهم.
يمكننا أن نتخيل أنه في أي لحظة يدور جسيمنا حول واحدة من النواة ، والتفاعل مع الثاني هو مجرد تصحيح. كوسيلة للدوران حول إحدى النواة ، يمكننا أن نفترض أن الإلكترون / الميون موجود في حالة الأرض (1 ثانية) ، وظيفة الموجة معروفة لنا جيدًا من الجزء السابق:

$$

$$| 1s \ rangle = \ frac {1} {\ sqrt {\ pi}} \ exp \ left (- \ frac {R} {R_1} \ right)$$

حيث $$$R_1$ هو نصف قطر بوهر للجسيمات. في حالة الإلكترون $$$R_1 = 1 دولا$ البورون (وهو نصف قطر بوهر للإلكترون ، يساوي حوالي 0.5 أنجستروم) ، وفي حالة الميون $$$R_1 = \ frac {1} {m_ \ mu} \ approx \ frac {1} {207}$ .
من أجل تقريب وظيفة موجة الإلكترون / الميون تقريبًا في مجال 2 نواة ، يمكننا محاولة اتخاذ التمثيل التالي:

$$

$$\ psi \ approx c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle$$

وبعد ذلك يتم تقليل مشكلة حل المعادلة التفاضلية الجزئية المعقدة معنا إلى البحث عن 2 من المعاملات غير المعروفة c ₁ و c ₂ . هذا هو المداري الجزيئي للغاية الذي يقدم كمجموع مع المعاملات (مزيج خطي من المدارات الذرية الذرية العلمية 1s).

بطبيعة الحال ، نحن بحاجة إلى معادلة لهذه المعايير. والحصول عليها بسيط للغاية إذا استبدلت هذا التقريب في معادلة شرودنجر $$$\ hat {H} \ psi = E \ psi$ :

$$

$$\ hat {H} (c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle) = c_1 \ hat {H} | 1s_1 \ rangle + c_2 \ hat {H} | 1s_2 \ rangle = E (c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle) = c_1 E | 1s_1 \ rangle + c_2 E | 1s_2 \ rangle$$

في الواقع ، نريد أن تكون هذه النسبة راضية في كل مكان ، حتى نتمكن من حساب متوسط ​​قيم كل هذا بطريقة أو بأخرى. نضرب هذه المعادلة على اليسار ب $$$<1s_1 |$ و $$$<1s_2 |$ ودمج على جميع الإحداثيات. نتيجة لذلك ، نحصل على نظام من معادلتين خطيتين حيث يكون من الضروري العثور على المعاملات c ₁ و c ₂ والطاقة E :

$$

$$\ تبدأ {pmatrix} \ langle 1s_1 | \ hat {H} | 1s_1 \ rangle & \ langle 1s_1 | \ hat {H} | 1s_2 \ rangle \\ \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle & \ langle 1s_2 | \ hat {H} | 1s_2 \ rangle \\ \ end {pmatrix} \ تبدأ {pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ تبدأ {pmatrix} \ \ langle 1s_1 | 1s_1 \ rangle & \ langle 1s_1 | 1s_2 \ rangle \\ \ langle 1s_2 | 1s_1 \ rangle & \ langle 1s_2 | 1s_2 \ rangle \\ \ end {pmatrix} \ تبدأ {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

أي شخص درس الجبر الخطي سيتعرف على مشكلة معايض الأضخم المعمم. قبل حلها ، سنقوم بتحليل ما تساوي عناصر المصفوفات 2 ، التوتا الحالية ، (وفي نفس الوقت نقدم تسمية قصيرة بحرف واحد).

• لنبدأ مع أبسط: $$$\ langle 1s_1 | 1s_1 \ rangle = \ langle 1s_2 | 1s_2 \ rangle = 1$ - هذا هو تطبيع وظائف الموجة ، وكما نذكر ، فإن الاحتمال الكلي لإيجاد الإلكترون / الميون هو واحد على الأقل في مكان ما.
• $$$\ langle 1s_1 | 1s_2 \ rangle = \ langle 1s_2 | 1s_1 \ rangle = S$ - هذا هو ما يسمى التداخل لا يتجزأ ، والتي تبين كيف تتداخل الغيوم الإلكترون 1S لكل من الذرات.
• $$$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_2 \ rangle = \ alpha$ . يتكون هذا المكمل من عدة أجزاء:
  

  $$

  $$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_1 | \ hat {H} _1 | 1s_1 \ rangle} _ {- \ frac {m} {2}} + \ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle + \ frac {1} {R}$$
  
  
• $$$\ langle 1s_1 | \ hat {H} | 1s_2 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ beta$ . هنا هو مشابه:
  

  $$

  $$\ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_2 | \ overbrace {\ hat {H} _1 | 1s_1 \ rangle} ^ {- \ frac {m} {2} | 1s_1 \ rangle}} {{\ frac {m} {2} S} + \ langle 1s_2 | \ قبعة {V} _2 | 1s_1 \ rangle + \ frac {S} {R}$$
  
  أي طاقة ذرة شبيهة بالهيدروجين وتنافر نووي ، تحجيمها بواسطة التداخل المتكامل (المصطلحان الأول والأخير) ، وكما كانت ، طاقة قفز الإلكترون / الميون من ذرة إلى أخرى.
  

دعونا نجد التعبيرات عن طاقات أيوننا الشبيه بالهيدروجين من المعادلة المعاد كتابتها كـ

$$

$$\ تبدأ {pmatrix} \ alpha & \ beta \\ \ beta & \ alpha \ end {pmatrix} \ تبدأ {pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ تبدأ {pmatrix} 1 & S \\ S & 1 \ end {pmatrix} \ start {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

للعثور على الطاقة التي تحتاجها لحل المعادلة:

$$

$$\ det \ start {pmatrix} \ alpha -E & \ beta -ES \\ \ beta - ES & \ alpha -E \ end {pmatrix} = (\ alpha -E) ^ 2 - (\ beta - ES) ^ 2 = 0 دولا$$

حيث تشير كلمة "det" إلى المحدد (المحدد لمصفوفة ، بالروسية).

حلول هذه المعادلة التربيعية فيما يتعلق E هي:

$$

$$E_ \ pm = \ frac {\ alpha \ pm \ beta} {1 \ pm S} = - \ frac {m} {2} + \ frac {1} {R} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

من الواضح أن القطعة الأولى هي طاقة الذرة ، والثانية هي الطرد النووي ، وهو نفس حاجز كولوم الذي يمنع اشتعال التفاعل النووي الحراري ، ويجب معالجة البنية المعقدة الأخيرة.

إذا تجاهلنا التنافر النووي ، الذي هو مجرد نقطة مرجعية لطاقة الإلكترون / الميون ، سنصل إلى أن لدينا دولتان مع الطاقة

$$

$$\ epsilon_ \ pm = - \ frac {m} {2} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

منذ كل وظيفة موجة $$$| 1s_1 \ rangle$ و $$$| 1s_2 \ rangle$ - إيجابي ، و $$$\ hat {V} _i <0$ (لأن الجسيم السلبي يوجه دائمًا إلى الموجب) ، إذن $$$\ epsilon_ + <- \ frac {m} {2}$ (طاقة ذرة واحدة) ، و $$$\ epsilon _-> - \ frac {m} {2}$ ، أي نحصل على صورة قياسية للمدارات الجزيئية:



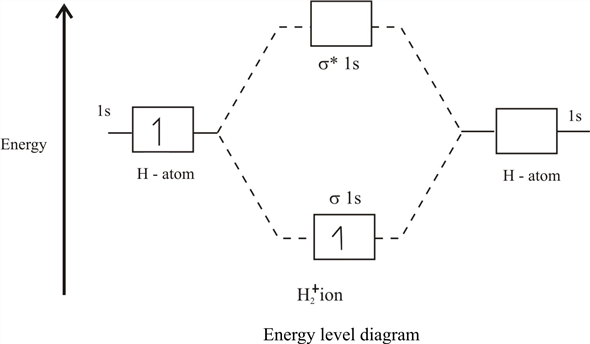
انخفاض المداري مع الطاقة $$$E _ +$ دعا ملزمة ، وأعلى (مع الطاقة $$$E _-$ ) - المضادة للربط ، أو تخفيف. نتيجة لذلك ، إذا كان الإلكترون / الميون يقع على المدار الجزيئي السفلي ، فإنه يستفيد من التحليق حول نويين أكثر من حوالي واحد ، ومع حركته ، فإنه يقلل من الطاقة الكلية للنظام. وهذا هو الرابط الكيميائي السحري للغاية الذي يراقب التنافر النووي ، مما يسمح للنواة بأن تكون بجانب بعضها لبعض الوقت.

وهنا يجب حساب مكملات الرابطة الكيميائية لفهم مدى قرب نواة الهيدروجين. في الواقع ، يتم احتساب جميع التكاملات الثلاثة المطلوبة بشكل تحليلي ، لكنها تتسم بالبواسير بشكل كبير ومعقدة (أي شخص مهتم ، انظر الفصل 9 في كتاب كيمياء الكم في Flary ). لذلك ، سوف نذهب بطريقة مختلفة ، أبسط ، وحساب هذه التكاملات عدديًا باستخدام طريقة مونت كارلو.

طريقة متروبوليس

أرى أنه من المنطقي للغاية في النص حول الطاقة النووية الحرارية أن أشيد بجدها: الذرة العسكرية ، وبشكل أكثر تحديداً ، مشروع مانهاتن . لقد نشأت منه طريقة مونت كارلو ، وخاصة خوارزمية متروبوليس ، أحد مؤلفيها ، إدوارد تيلر ، هو "أب القنبلة الهيدروجينية" (أي الشخص الذي أطلق الانصهار النووي الحراري على Envetok Atoll).


بشكل عام ، سنقوم بتحليل جوهر الطريقة. الغرض منه هو مهام الميكانيكا الإحصائية. التوزيع الرئيسي فيه هو توزيع بولتزمان: احتمال اكتشاف نظام في حالة معينة هو $$$\ exp (- \ beta E)$ . $$$\ beta ^ {- 1} = k_ \ mathrm {B} T$ . والقيمة المرصودة لبعض المعلمات A للنظام في توازن الديناميكا الحرارية تساوي التكامل

$$

$$\ langle A \ rangle = \ frac {1} {Z} \ int A (q) \ exp (- \ beta E (q)) dq$$

حيث q هي الإحداثيات التي تحدد حالة النظام (على سبيل المثال ، إحداثيات / عزم الدوران للجسيمات) ، و Z هي عامل التطبيع الذي يسمى وظيفة التقسيم:

$$

$$Z = \ int \ exp (- \ beta E (q)) dq$$

إذا كان هناك الكثير من الجسيمات الموجودة في النظام ، فلن يكون حساب أي من المكونات الموجودة في الجبهة أمرًا غير واقعي تمامًا. إن طريقة مونت كارلو الساذجة ، التي نختار فيها ببساطة مجموعة من إحداثيات q العشوائية ، لن تعطي أي شيء مفيدًا إذا كانت هناك حالات محتملة بالفعل للنظام حيث الاحتمال $$$\ exp (- \ beta E)$ غير الصفر بشكل ملحوظ ، عدد قليل جدا. وفي حالات مثل هذه بالتحديد ، نحتاج إلى عينة من حيث الأهمية ، حيث نسمح للخوارزمية بأخذ عينات من الأماكن المحتملة بشكل كافٍ فقط في مساحة الولاية.

تبدو خوارزمية متروبوليس كما يلي.

1. عند بدء المحاكاة ، نختار بعض تقريب البدء في مساحة التكوين $$$\ mathbf {q} ^ {(0)}$ وبعض المتجهات من الزيادة القصوى الممكنة $$$\ delta \ mathbf {q}$ . عند نقطة البداية ، نحسب طاقة النظام $$$E ^ {(0)} = E (\ mathbf {q} ^ {(0)})$ (قراءة - الاحتمال $$$p = \ exp (- \ beta E ^ {(0)})$ ).
2. التكوين الجديد في الخطوة nth كما يلي.
   
   1. احسب طاقة التكوين التجريبي $$$E_ \ mathrm {trial} = E (\ mathbf {q} _ \ mathrm {trial})$ (أي الاحتمال $$$p_ \ mathrm {trial} = \ exp (- \ beta E_ \ mathrm {trial})$ ).
   2. ثم نقارن الاحتمال القديم $$$p ^ {(n)}$ مع المحاكمة $$$p_ \ mathrm {trial}$
      
      
      • إذا كان التكوين الجديد لديه احتمال أكبر أو واحد ( $$$\ frac {p_ \ mathrm {trial}} {p ^ {(n)}} \ geq 1$ ) ، أو ، معادلًا ، تكون طاقة النقطة الجديدة أقل أو كما هي في القديم ( $$$E_ \ mathrm {trial} \ leq E ^ {(n)}$ ) ، ثم يتم قبول النقطة الجديدة ويذهب النظام إلى ذلك ( $$$q ^ {(n + 1)} = q_ \ mathrm {trial}$ )
      • إذا كان التكوين التجريبي أعلى في الطاقة ( $$$E_ \ mathrm {trial}> E ^ {(n)}$ ) ، وهو ما يعادل $$$\ frac {p_ \ mathrm {trial}} {p ^ {(n)}} <1$ ، ثم في هذه الحالة نقوم بإنشاء رقم عشوائي $$$P \ in [0؛ 1)$ من توزيع موحد ، ومقارنته مع نسبة الاحتمالات ، والتي هي احتمالات الانتقال. إذا $$$P <\ frac {p_ \ mathrm {trial}} {p ^ {(n)}}$ ، ثم نقبل نقطة جديدة ، وإذا لم يكن الأمر كذلك ( $$$P \ geq \ frac {p_ \ mathrm {trial}} {p ^ {(n)}}$ ) ، ثم نرفض ، ويبقى النظام في التكوين القديم ( $$$q ^ {(n + 1)} = q ^ {(n)}$ ) ...
      
      
   
   
3. باتخاذ العديد من الخطوات وفقًا للخوارزمية الموضحة أعلاه ، فإننا نأخذ عينات من جزء مهم (أي مهم حقًا) من المساحة المحتملة لتكوينات النظام. يتم احتساب تكامل الاهتمام بالنسبة لنا من خلال الصيغة:
   $$$\ langle A \ rangle = \ frac {1} {Z} \ int A (\ mathbf {q}) \ exp (- \ beta E (\ mathbf {q})) d \ mathbf {q} = \ frac { 1} {N} \ sum_ {n = 0} ^ {N} A (\ mathbf {q} ^ {(n)})$
   

هذه هي الطريقة التي تعمل خوارزمية متروبوليس.

والآن سيكون من الضروري تكييفه مع حساب التكاملات الثلاثة التي تهمنا. دعونا ننظر إليهم بمزيد من التفصيل.

• $$$S (R) = \ langle 1s_2 | 1s_1 \ rangle = \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- - \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-m \ underbrace {| \ mathbf {r} - \ mathbf {r} _2 | } _ {R_2})} _ {1s_2}} ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-m \ underbrace {| \ mathbf {r} - \ mathbf {r} _1 |} _ {R_1})} _ {1s_1}}} ^ {p (\ mathbf {r})} dx dy dz$ حيث $$$\ mathbf {r} = (x، y، z) ^ \ mathbf {T}$ - إحداثيات الإلكترون / الميون ، $$$\ mathbf {r} _i = (x_i ، y_i ، z_i) ^ \ mathbf {T}$ هي إحداثيات نواة الهيدروجين و $$$R_i = | \ mathbf {r} - \ mathbf {r} _i | = \ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2 + (z-z_i) ^ 2}$ - المسافات بين الجسيمات الموجبة والسالبة ،
  
• $$$\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ حدود _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1} \ frac {1} {R_2} } ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1}} ^ {p (\ mathbf {r})} dxdydz$
• $$$\ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ حدود _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_2)} _ {1s_2} \ frac {1} {R_1} } ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1}} ^ {p (\ mathbf {r})} dxdydz$

يمكن ملاحظة أنه إذا قمنا بحساب دالة 1s لإحدى الذرات للاحتمال p ،


ثم كل شيء آخر تحت علامة التكامل (وظيفة الموجة الثانية وفي 2 من 3 حالات من المحتمل أن تجذب الإلكترون / الميون إلى النواة) ستكون دالة يتم حساب متوسط ​​قيمتها. الشيء الوحيد الذي يجب القيام به ، على عكس الحساب المعتاد بواسطة طريقة متروبوليس ، هو تقويم تطبيع التكاملات. الحقيقة هي أن التطبيع القياسي سيكون على

$$

$$Z = \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ exp (-m R) dx dy dz = 4 \ pi \ int \ limit_ {0} ^ {+ \ infty} \ exp (-m R) R ^ 2 dR = \ frac {8 \ pi} {m ^ 3}$$

ونحن بحاجة إلى التطبيع ل $$$\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}$ حيث

$$

$$\ langle 1s_1 | 1s_1 \ rangle = \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ exp (-2 m R) dx dy dz = 4 \ pi \ int \ limit_ {0} ^ {+ \ infty} \ exp (-2m R) R ^ 2 dR = \ frac {\ pi} {m ^ 3}$$

هذا يعني أن كل جزء لا يتجزأ محسوب وفقًا لمتروبوليس سيحتاج إلى ضرب بعامل

$$

$$\ frac {Z} {\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}} = 8 \ sqrt {\ frac {\ pi} {m ^ 3}}$$

يمكن بالفعل ترتيب هذا في شكل برنامج نصي معين ، على سبيل المثال ، في Python (على سبيل المثال ، الرمز أدناه).


باستخدام مثل هذه الحسابات ، يمكننا أخيرًا مقارنة الطاقات المحتملة في أيون الهيدروجين $$$\ mathrm {H} _2 ^ +$ ونظيره muon.

$$$\ mathrm {H_2 ^ + = p ^ + e ^ - p ^ +}$ مقابل $$$\ mathrm {p ^ + \ mu ^ - p ^ +}$

لذلك ، مسلحين بنص ، يمكننا حساب سطح الطاقة المحتملة لمقاربة نواة الهيدروجين المرتبطة بإلكترون وميون. كنقطة مرجعية للطاقة ، نأخذ الذرات المخففة بلا حدود من بعضها البعض (أي ، $$$-m / 2$ ، وهو ما يساوي القدرة على المسافة بين النواة $$$R = + \ infty$ ).

في حالة الإلكترون ، تبدو الإمكانات القريبة من الحد الأدنى كما يلي:



يحدث الحد الأدنى على مسافة حوالي 2 البورون (أي ما يقرب من مجموع نصفين ذريين) ، والطاقة تفكك الجزيء إلى شظايا ما يقرب من 0.06 هارتري ، وهو ما يتوافق مع التدفئة إلى حوالي 20،000 درجة كلفن (أو مئوية ، لا يهم هنا). لتحويل الطاقات ، أوصي باستخدام الموارد عبر الإنترنت ، مثل هذا .

حالة مماثلة مع أيون الهيدروجين ملزمة muonally:



نظرًا لأن نصف قطر Bohr لهيدروجين الميون أصغر (انظر الجزء السابق ) ، فإن نوى الهيدروجين تقارب 200 مرة تقريبًا عند الحد الأدنى من الطاقة المحتملة. طاقة الانهيار لهذا الجزيء هي بالفعل أكثر من 10 هارتري ، وهو ما يتوافق مع درجة حرارة تزيد على ثلاث درجات ليايم ( $$$\ تقريبا (3.2 \ cdot 10 ^ 6) ^ \ circ$ ).

في حالة الاشتعال ، تتطلب التفاعلات عادة درجة حرارة تصل إلى 10 ⁸ K ، أي حوالي 320 Hartree. دعونا نرى ما هي المسافة التي تتحقق فيها طاقة مماثلة في حالة divodoron ion العادي وفي حالة نسختها muon:



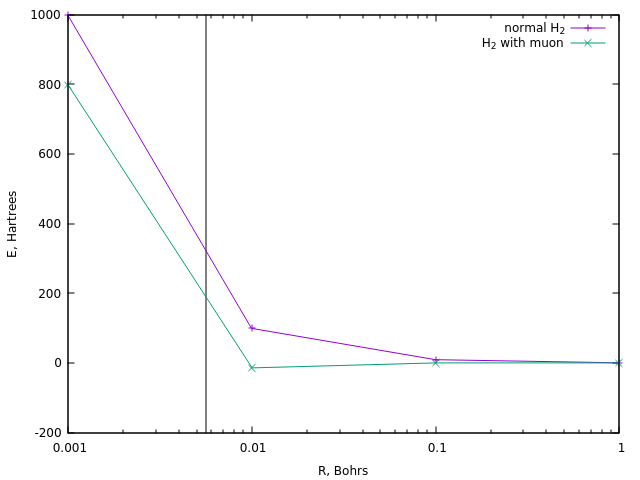
في حالة الأولى ، وهذا يتوافق مع مسافة حوالي 0.0058 البورون (الخط العمودي).

يتم تحقيق مسافة مماثلة في هيدروجين الميون عند طاقة تبلغ حوالي 190 هكتار ، أي حوالي واحد ونصف مرات أقل. وهذا هو أبسط تقدير لدرجة حرارة تحفيز الميون.

ولكن في الواقع ، سيكون كل شيء أكثر برودة. والحقيقة هي أنه إذا تم تشكيل جسيم مستقر $$$\ mathrm {({} ^ mH (\ mu ^ -) {} ^ nH) ^ +}$ ، ثم تتأرجح هذه النوى ، بينما يكون الميون على قيد الحياة ، بالنسبة لبعضها البعض. وهنا يمكن أن يحدث نفق من حالة "ذرتين هيدروجين" إلى حالة "نواة أثقل" ، ويعتمد احتمال النفق على طول النفق المطلوب د تقريبًا $$$p ^ {- d}$ ، حتى نتمكن من التقريب بين النواة معًا بواسطة الميون ، فإننا سنزيد بشكل كبير من احتمال مسار النفق في هذا التفاعل. لسوء الحظ ، لم تعد تقديرات هذا التأثير تتطلب كيمياء الكم ، ولكن الفيزياء النووية ، لذلك هذا الجزء من المناقشة خارج نطاق هذا المنصب. لذلك على هذا سوف نتوقف.

PS لماذا هو ليس بهذه البساطة؟

في الواقع ، لتكوين هذه الجسيمات ليست بهذه البساطة في ظروف البلازما. والحقيقة هي أنه إذا اصطدمنا بجسيمين ، فمن الواضح أن طاقتهما الإجمالية تتجاوز طاقة التفكك (أو التأين ، في حالة النواة + الإلكترون / الميون) ، لذلك عندما تصطدم ، فإنها لا تشكل جسيمًا مستقرًا (ذرة ، أيون ، جزيء) ، ولكن الماضي بعضها البعض. لكي يتمسكوا ببعضهم البعض ، يحتاجون إلى التخلص من فائض الطاقة في مكان ما ، ولهذا نحتاج إلى ثالث إضافي سيتولى هذه الطاقة. يمكن أن يكون فوتونًا ، أو نوعًا من الجسيمات اليسرى تحلق في مكان قريب ، ولكن الشيء الرئيسي هو أن الظروف يجب أن تساهم في هذا التحمل للطاقة الزائدة.

PPS

إذا كان لديك أي تعليقات / توضيحات / أسئلة ، فاكتب في التعليقات أو في PM. سأصحح كل شيء ، سأجيب وأشرح كل شيء.