🙍🏾 🐋 ⚰️ أنواع اللانهاية وجذع الدماغ ➰ 🍿 🤳🏾

هذا المقال هو استمرار لمقال عن أعداد ضخمة . ولكن الآن سنذهب أبعد من ذلك - في ما لا نهاية اللانهاية.

لهذا نحن بحاجة إلى ZFC - نظرية مجموعات Zermelo ، Frenkel + Choice. الاختيار هو بديهية الاختيار ، والأكثر إثارة للجدل من الناحية النظرية مجموعة نظرية. إنها تستحق مقالة منفصلة. من المفترض أن تعرف ما هي "قوة" المجموعة. إن لم يكن ، ثم google ، بالتأكيد هذا هو أفضل مما أستطيع. هنا سوف أذكر فقط بعض

حقائق معروفة

يشار إلى قوة مجموعة من الأعداد الصحيحة $\ aleph_0$ . هذه هي القوة اللانهائية الأولى ؛ وتسمى هذه المجموعات بالعد.
قوة أي مجموعة فرعية لا حصر لها من الأعداد الصحيحة هي بسيطة ، حتى ، الخ - تحصى أيضا.
مجموعة الأرقام المنطقية ، أي الكسور p / q ، يمكن حسابها أيضًا ؛ يمكن تمريرها عن طريق الثعبان.
لأي قوة ، هناك عملية باورست - مجموعة جميع المجموعات الفرعية التي تخلق طاقة أكثر من المجموعة الأصلية. في بعض الأحيان يشار إلى هذه العملية بأنها ترفع اثنين إلى قوة ، أي $powerset (\ aleph_0) = 2 ^ {\ aleph_0} = \ aleph_c$ . poweret من القوة المحسوبة هي قوة التواصل.
تمتلك القدرة المتواصلة من قبل: قطاعات محدودة وغير محدودة ، والأشكال المستوية والحجمي ، وحتى المساحات ذات الأبعاد n ككل
للرياضيات العادية ، والقوة التالية ، $poweret (\ aleph_c)$ غير مطلوبة عملياً ، عادةً ما يحدث كل العمل مع مجموعات قابلة للعد ومجموعات طاقة متصلة

الآن

حقائق غير معروفة

في ZFC ، لا يمكن تعيين كل مجموعات العناصر. هناك مجموعات واسعة جدًا بحيث يتعذر السماح لها بأن تكون مجموعات ؛ تنشأ مفارقات. على وجه الخصوص ، " مجموعة جميع المجموعات " ليست مجموعة. ومع ذلك ، هناك نظريات مجموعة حيث يسمح مثل هذه المجموعات.

وعلاوة على ذلك. وضع النظرية ... ما الأشياء؟ الأرقام؟ تفاحة؟ البرتقال؟ الغريب ، ZFC لا يحتاج إلى أي كائنات. خذ المجموعة الفارغة {} وتوافق على أنه يعني 0. 1 تشير بواسطة {{}} الشرح كـ {{{}}} وهكذا. {5،2} هو {{{{{{{}}}}}}} ، {{{}}}}. باستخدام الأعداد الصحيحة ، يمكننا إنشاء أشكال حقيقية ، ويمكن لمجموعات الأشكال الحقيقية إنشاء أي أشكال.

لذلك نظرية مجموعة ... كيف أقول ... نظرية جوفاء. هذه النظرية ليست عن شيء. بتعبير أدق ، حول الكيفية التي يمكنك بها تداخل (تداخل العش ، أي ، وضع كل منها في الأخرى) الأقواس.

العملية الوحيدة المحددة في نظرية المجموعة هي

$\ في$ - رمز الانتماء. ولكن ماذا عن التوحيد والاستبعاد والمساواة ، وما إلى ذلك؟ هذه كلها وحدات ماكرو ، على سبيل المثال:

$(A = B) \ equiv \ forall x ((x \ in A) = (x \ in B))$

أي أنه في الترجمة إلى اللغة الروسية ، يتم اعتبار مجموعتين متماثلتين عندما نحصل على نفس النتائج عند اختبار أي عنصر للانتماء إليها.

لم يتم ترتيب المجموعات ، ولكن يمكن إصلاح ذلك: اسمح للزوج المرتبة (p ، v) {{p} ، {p، v}}. غير مستحسن من وجهة نظر المبرمج ، ولكن يكفي لعالم الرياضيات. الآن مجموعة من جميع أزواج القيمة البارزة تعين وظيفة ، والتي هي الآن أيضا مجموعة! إت فويلا! كل التحليل الرياضي ، الذي يعمل على مستوى لغات الدرجة الثانية ، لأنه لا يتحدث عن وجود أرقام ، ولكن عن وجود وظائف ، ينهار إلى لغة من الدرجة الأولى!

وهكذا ، فإن نظرية المجموعات هي نظرية سيئة بدون كائنات ، ولديها أيقونة علاقة واحدة ، لها قوة وحشية على الإطلاق - دون أي افتراضات جديدة ، فإنها تولد من نفسها حسابًا رسميًا وأرقامًا حقيقية وتحليلًا وهندسة وأكثر من ذلك بكثير. هذا هو نوع من الرياضيات TOE.

فرضية التواصل - CH

هل هناك قوة بين

$\ aleph_0$ و

$2 ^ {\ aleph_0}$ ؟ لم تستطع كانتور حل هذه المشكلة ؛ فقد أشاد "ملك علماء الرياضيات" هيلبرت بأهميتها ، لكن في وقت لاحق فقط ثبت أن هذه الفرضية لا يمكن إثباتها أو دحضها. إنها مستقلة عن ZFC.

هذا يعني أنه يمكنك إنشاء حسابين مختلفين: واحد باستخدام ZFC + CH ، والآخر باستخدام ZFC + (وليس CH). في الواقع ، حتى أكثر من اثنين. لنفترض أننا نرفض CH ، أي أننا سنؤمن بذلك

$\ aleph_0$ و

$2 ^ {\ aleph_0}$ لا تزال هناك قوة. كم يمكن أن يكون هناك؟ واحد ، اثنان؟ يعتقد غودل أن واحد فقط. ولكن ، كما اتضح فيما بعد ، فإن افتراض وجود 2 ، 17 ، 19393493 منهم لا يؤدي إلى تناقضات. أي رقم ، ولكن ليس لانهائي!

عندما نتوصل في حساب رسمي إلى بيان غير قابل للإثبات ، ولأسباب معينة نعلم أن هذا البيان ، رغم أنه غير قابل للإثبات ، هو في الحقيقة صواب أو خطأ. من الناحية النظرية ، لا يعمل هذا الأمر ، فنحن نحصل على علماء رياضيات مختلفين حقًا. كيف تتصل بهذا؟ هناك ثلاثة مناهج فلسفية:

الشكلية: لماذا ، في الواقع ، أن يفاجأ؟ وضعنا قواعد لعبة الرموز وقواعد مختلفة - نتيجة مختلفة. لا حاجة للبحث عن مشكلة حيث لا وجود لها

الأفلاطونية: لكن كيف يمكن إذن شرح أن نظريات مختلفة تمامًا ، مثل ZFC و New Foundations ، المبنية على مبادئ مختلفة تمامًا ، تعطي دائمًا نفس النتيجة تقريبًا؟ هل هذا يعني أن وراء الصيغ نوع من الواقع الذي ندرسه؟ تم عقد هذا الرأي ، على سبيل المثال ، من قبل غودل

الكون المتعدد: يمكن أن يكون لدينا العديد من البديهيات ، وفي بعض الأحيان نعطي نفس النتيجة ، وأحيانًا لا. يجب أن ندرك الصورة بأكملها - إذا كان اللون مرتبطًا بأنظمة مختلفة من البديهيات ، فإن شجرة التأثيرات الملونة هي الرياضيات. إذا كان هناك شيء صحيح في كل مكان - فهو أبيض ، ولكن هناك أيضًا فروع ملونة.

أعلى وأعلى.

في المستقبل ، من أجل البساطة ، سوف نقبل فرضية الاستمرارية ، أي

$powerset $ (\ aleph_0) = \ aleph_1 = \ aleph_c $$ - انها مريحة جدا. في الواقع ، سوف نقبل أيضًا البديهية الأقوى ، وهي فرضية الاستمرارية المعممة التي تقول إن بين x و powerset (x) لا توجد أبدًا أي قوى وسيطة. الآن نكرر مجموعة القوى وكل شيء بسيط:

$\ aleph_0 \ rightarrow \ aleph_1 \ rightarrow \ aleph_2 \ rightarrow ... \ rightarrow \ aleph_ {36463634} \ rightarrow$

إلى أي مدى يمكننا أن نذهب؟ بعد عدد لا حصر له من التكرارات ، وصلنا إلى

$\ aleph_ \ omega$ - قوة لا حصر لها في النظام! بالمناسبة ، لم يكن وجودها واضحًا للكانتور. لكن ثانية! بعد كل شيء ، يتم تعريف وظيفة powerset دائما ، لذلك

$\ aleph_ \ omega$ لا يمكن أن يكون الأخير!

$\ aleph_ \ omega \ rightarrow \ aleph _ {\ omega + 1} \ rightarrow \ aleph _ {\ omega + 2} \ rightarrow ...$

للحصول على

$\ aleph _ {\ omega + 3}$ فمن الضروري أن يكرر powerset اللانهاية وثلاث مرات أخرى . هل بدأت بالفعل في هدم السقف؟ وإلا سيكون كذلك. لأنه مرة أخرى ، بعد أن تكررت poweret عدد لا حصر له من المرات ، وصلنا إلى

$\ aleph _ {\ omega + \ omega} = \ aleph _ {\ omega2}$ ، وبعد ذلك ، بطبيعة الحال ،

$\ aleph _ {\ omega2 + 1}$

بعد أن وصلت إلى ما لا نهاية عدد لا حصر له من المرات ، نحصل على الفهرس

$\ omega ^ 2$ . كيف تحب هذه القوة ، على سبيل المثال:

$\ aleph _ {\ omega ^ 3 + \ omega ^ 2 + \ omega4 + 48745}$ ؟ على الرغم من أننا تكررت poweret على قائمة المراسيم ، وفيما يلي المراسيم الأولية:

ولكن هناك الكثير والكثير. لذلك سوف نتخطى كل ذلك على الفور ونفعل ذلك

خطوة كبيرة على الفور

تحذير! ما هو مكتوب أدناه قد يكون خطرا على عقلك! قمنا بتكرار مجموعة باورست عددًا لا يحصى من المرات ، لكن ألا نلاحظ ذلك في السلسلة ؟ بصراحة ، أنا نفسي من النقانق قليلاً من حقيقة أن الدورة يمكن أن تؤدي سلسلة متصلة من الأوقات ، ولكن نظرية المجموعة تتطلب وجود

$\ aleph _ {\ aleph_1}$

التالي سنذهب بشكل أسرع:

$\ aleph _ {\ aleph_1} \ rightarrow \ aleph _ {\ aleph_2} ... \ rightarrow \ aleph _ {\ aleph_ \ omega} = \ aleph _ {\ aleph_ \ aleph} \ rightarrow$

يحتوي مؤشر Alef الأخير على مؤشر الصفر ، لكن اللاتكس المحلي لا يسمح بوضعه - فهناك العديد من المستويات. لكن الأهم من ذلك ، فهمت أنه ، بغض النظر عن مقدار القوة الوحشية الجديدة التي سننشئها ، يمكننا أن نقول - نعم ، هذا مجرد مكرر ، ووضع هذا البناء بالكامل في أليف جديد كمؤشر. الآن تنمو القدرات مثل كرة الثلج ، لا يمكننا إيقافها ، هرم أليفز أعلى ويمكننا إنشاء أي قوة ... أم لا؟

قوة غير قابلة للوصول

ماذا لو كان هناك قوة كبيرة جدا

$\ theta$ لا يهم كيف نحاول الوصول إليها "من الأسفل" ، بناء الهياكل من ألفس ، ونحن لن نحقق ذلك؟ اتضح أن وجود مثل هذه السلطة مستقلة عن ZFC. يمكنك قبول وجودها أم لا.

أسمع الهمس من الحلاقة Occam ... لا ، لا. يلتزم علماء الرياضيات بالمبدأ المعاكس ، وهو ما يسمى التطرف الأنطولوجي - دع كل شيء ممكن موجودًا. ولكن هناك سببان آخران على الأقل أرغب في قبول هذه الفرضية.

أولاً ، هذه ليست أول قوة غير قابلة للتحقيق نعرفها. أولاً ... هذه هي قوة العد المألوفة. الغريب ، أنه يحتوي على جميع الخصائص التي يتعذر الوصول إليها - ليس من المعتاد أن نسميها ما يلي:
لا توجد وسيلة للحصول على طاقة لا نهائية "من الأسفل" - لا تضيف العناصر عددًا محدودًا من المرات ، ولا تكرّر poweret () عددًا محدودًا من المرات ، باستخدام مجموعات محدودة للبذر ، فلن تحصل على ما لا نهاية. للحصول على ما لا نهاية ، يجب أن يكون لديك بالفعل في مكان ما.
يتم تقديم وجود القوة اللانهائية من خلال البديهية الخاصة - بديهية اللانهاية. وبدون ذلك ، فإن وجود قوة لا نهائية أمر لا يمكن إثباته.

ثانيًا: إذا رفضنا بديهية اللانهاية ، فسنحصل على FinSet ، وهي نظرية مجموعة ألعاب بسيطة مع مجموعات محدودة. لنكتب كل هذه المجموعات (ما يسمى بنظرية النظرية )

{}
{} {}
{{{}} ، {}}
{{{{}}}}
{{{{}}} ، {{}}}
{{{{}}} ، {{}}}
{{{{}}} ، {{}} ، {}}
...

ونحصل على ... مجموعة لا حصر لها من مجموعات محدودة ... وهذا هو ، لنظرية نظرية مجموعات محدودة هو لانهائي ، وتلعب دور "مجموعة من كل مجموعات" في ذلك. ربما يساعد هذا في فهم سبب عدم قدرة النظرية على الحديث عن "مجموعة كل المجموعات" - مثل هذه المجموعة موجودة دائمًا كنموذج خارج النظرية ولديها خصائص أخرى غير المجموعات الموجودة في الداخل. لا يمكنك إضافة اللانهائي لنظرية المجموعات المحدودة.

ونعم

$\ theta$ هذا هو "العديد من جميع التعدد" لنظرية ZFC. في هذا الفيديو ، في النهاية ، يُقال بشكل جميل عن القوة التي لا يمكن الوصول إليها ، لكن علينا أن نواصل.

أبعد من ذلك.

بالطبع ، يمكننا أن نذهب أبعد من ذلك عن طريق التكرار

$poweret (\ theta)$ . بعد اجتياز جميع الخطوات الموضحة أعلاه ، بناء أبراج مكررة ضخمة ، نواجه مرة أخرى كاردينالًا بعيد المنال (لكننا الآن لا نحتاج إلى بديهيات جديدة ، مع البديهية لوجود قوة غير قابلة للتحقيق والتي أضفناها للتو ، أصبح هذا أمرًا قابلاً للإثبات). مرارا وتكرارا.

$\ theta_0 \ rightarrow \ theta_1 \ rightarrow \ theta_2 \ rightarrow ... \ rightarrow \ theta_ {36463634} \ rightarrow$

لاحظ أن السهم الآن غير منطقي بالنسبة لنا مثل تنفيذ دالة Powerset () ، ولكن GetNextInaccessible (). خلاف ذلك ، كل شيء يبدو مشابهاً للغاية ، لدينا:

$\ theta _ {\ theta_1} \ rightarrow \ theta _ {\ theta_2} ... \ rightarrow \ theta _ {\ theta_ \ omega} \ rightarrow \ theta _ {\ theta_ \ theta} \ rightarrow$

الآن ثم سنحقق بالتأكيد أي شيء ... أم لا؟

التسلسل الهرمي للقدرات الكبيرة.

نعم ، مع GetNextInaccessible ، نواجه قوة لا يمكن الوصول إليها بشكل مفرط. وجودها يتطلب واحدة أكثر بديهية. هناك قوى مفرطة لا يمكن الوصول إليها. و هكذا. ولكن هناك طرق أخرى لتحديد القوة ، ليس فقط من خلال عدم إمكانية الوصول:

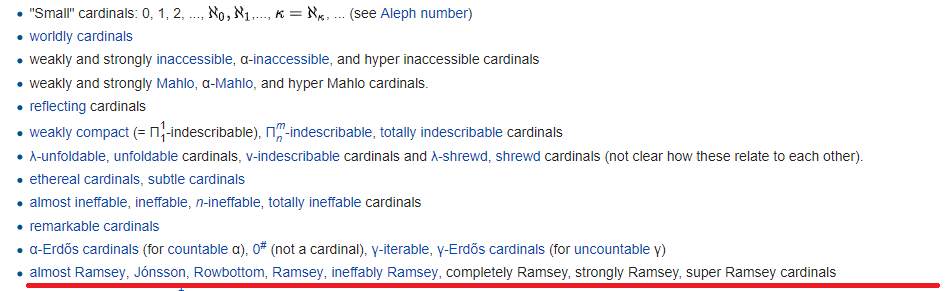
خلف كل رابط ، كقاعدة عامة ، هناك تسلسل هرمي لا نهاية له مع عدد تعسفي من بادئات hyper-and repeater. ومع ذلك ، فإن العدد الإجمالي للصيغ التي تحدد الكرادلة غير قابلة للتحقيق ليس بهذا الحجم - لأن عدد الصيغ يمكن حسابه !!! لذلك ، عاجلا أو آجلا سوف تنتهي. حيث ينتهي ، يتم رسم خط أحمر. يتم تعريف كل شيء أسفل هذا الخط بطريقة غير مستقرة ، وإن كان ذلك رسميًا.

يشير الخط الأحمر نفسه إلى نهاية كون جودل (لكن لا تنسَ أن جودل قد خلق أكوانين مختلفين) - عالم مجموعات مكونة من الأسفل باستخدام الصيغ. تسمى السعات الموجودة فوق الخط الأحمر hmm ، "صغيرة" ، وأسفل - كبيرة:

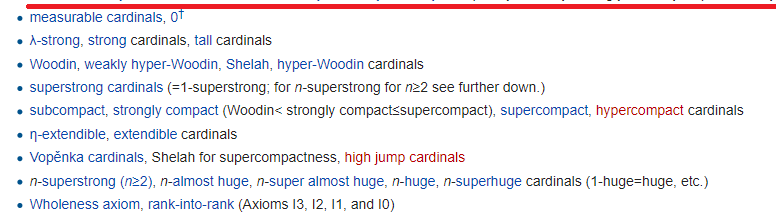
الفكرة الأساسية فيها هي أن عالم المجموعات يصبح كبيرًا لدرجة أنه يبدأ في تكرار نفسه بمعنى مختلف. كل سطر ، كما هو الحال دائما ، يتطلب بديهية منفصلة ، وعدة. والأكثر إثارة للاهتمام ، كل هذا ليس عديم الفائدة كما قد تظن. على سبيل المثال ، هناك حاجة إلى البديهية الأقوى (رتبة إلى رتبة) ، في الخلاصة ، لإثبات حقيقة الأقراص .

يوجد أدناه استطلاع ، يتم فك تشفير الخيار الأخير هنا .

أنواع اللانهاية وجذع الدماغ