لا ، حسنًا ، بالطبع ، لست جادًا. يجب أن يكون هناك حد لمدى إمكانية تبسيط الموضوع. لكن بالنسبة للمراحل الأولى ، فهم المفاهيم الأساسية و "الدخول" السريع إلى الموضوع ، فقد يكون ذلك مسموحاً به. وكيفية تسمية هذه المادة بشكل صحيح (الخيارات: "التعلم الآلي للدمى" ، "تحليل البيانات من الحفاضات" ، "الخوارزميات الأصغر") ، سنناقش في النهاية.
لرجال الأعمال. وقد كتب العديد من برامج التطبيق على MS Excel لتصور وتصور العمليات التي تحدث في طرق مختلفة للتعلم الآلي عند تحليل البيانات. في النهاية ، تصوَّر الرؤية وفقًا لوسائل الإعلام الخاصة بالثقافة التي طورت معظم هذه الأساليب (بالمناسبة ، بأي حال من الأحوال. إن أقوى "وسيلة متجه للدعم" ، أو SVM ، تعد آلة متجه الدعم بمثابة اختراع لمواطننا فلاديمير فابنيك ، معهد موسكو للإدارة. 1963 ، بالمناسبة ، الآن هو يعلم ويعمل في الولايات المتحدة الأمريكية).
ثلاثة ملفات للمراجعة
1. K- يعني التجميع
تتعلق المهام من هذا النوع بـ "التعلم بدون معلم" ، عندما نحتاج إلى تقسيم البيانات الأولية إلى عدد معين من الفئات المعروفة مسبقًا ، لكن ليس لدينا أي عدد من "الإجابات الصحيحة" ، يجب أن نستخلصها من البيانات نفسها. المشكلة الكلاسيكية الأساسية لإيجاد سلالات من زهور القزحية (رونالد فيشر ، 1936!) ، والتي تعتبر العلامة الأولى لهذا المجال من المعرفة - هي من هذه الطبيعة.
طريقة بسيطة جدا. لدينا مجموعة من الكائنات الممثلة كمتجهات (مجموعات من أرقام N). بالنسبة للقزحية ، هذه مجموعات مكونة من 4 أرقام تميز الزهرة: طول وعرض فصوص الشريان الخارجي والداخلي ، على التوالي (
Iris Fisher - Wikipedia ). كمسافة ، أو كمقياس للقرب بين الأشياء ، يتم اختيار القياس الديكارتي المعتاد.
علاوة على ذلك ، يتم اختيار مراكز المجموعات بشكل تعسفي (أو ليس تعسفيًا ، انظر أدناه) ، ويتم حساب المسافات من كل كائن إلى مراكز المجموعات. يتم تمييز كل كائن في خطوة التكرار هذه على أنه ينتمي إلى أقرب مركز. ثم يتم نقل مركز كل مجموعة إلى الوسط الحسابي لإحداثيات أعضائها (عن طريق القياس مع الفيزياء يطلق عليه أيضًا "مركز الكتلة") ، ويتم تكرار الإجراء.
تتلاقى العملية بسرعة كافية. في الصور ذات البعدين ، يبدو كما يلي:
1. التوزيع العشوائي الأولي للنقاط على الطائرة وعدد التجمعات

2. تحديد مراكز المجموعات وتخصيص النقاط لمجموعاتها
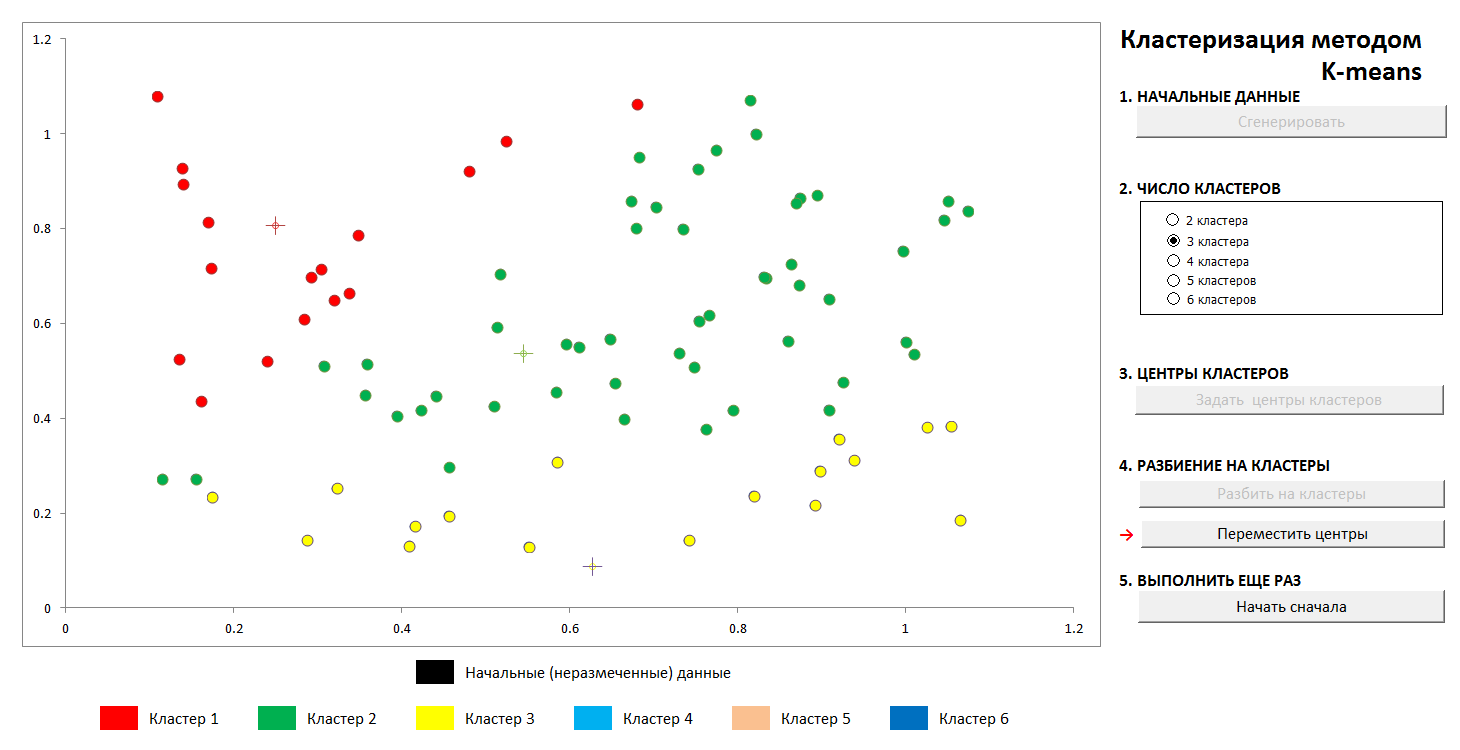
3. نقل إحداثيات مراكز الكتل ، إعادة حساب النقاط ، حتى تستقر المراكز. مسار مركز الكتلة إلى الموضع النهائي مرئي.

في أي وقت ، يمكنك تعيين مراكز كتلة جديدة (دون إنشاء توزيع جديد للنقاط!) ونرى أن عملية التقسيم ليست فريدة من نوعها دائمًا. من الناحية الرياضية ، هذا يعني أنه بالنسبة للوظيفة المحسنة (مجموع مربعات المسافات من النقاط إلى مراكز مجموعاتها) ، فإننا لا نجد الحد الأدنى العام ، ولكن الحد الأدنى المحلي. يمكن هزيمة هذه المشكلة إما عن طريق اختيار غير عشوائي للمراكز الأولية للمجموعات ، أو عن طريق فرز المراكز المحتملة (في بعض الأحيان يكون من المفيد وضعها في نقطة معينة بالضبط ، ثم هناك على الأقل ضمانة بأننا لن نحصل على مجموعات فارغة). في أي حال ، فإن المجموعة المحدودة لها دائمًا حد أدنى صحيح.
يمكنك اللعب باستخدام هذا الملف على هذا الرابط (لا تنس تمكين دعم الماكرو. يتم فحص الملفات بحثًا عن الفيروسات)
وصف طريقة ويكيبيديا -
طريقة الوسائل k2. تقريب كثيرات الحدود وانهيار البيانات. إعادة التعليم
عالم بارز ومتعميم لعلوم البيانات K.V. يتحدث فورونتسوف باختصار عن أساليب التعلم الآلي باعتبارها "علم منحنيات الرسم من خلال نقاط". في هذا المثال ، سنعثر على النمط في البيانات بطريقة المربعات الصغرى.
يظهر أسلوب تقسيم البيانات المصدر إلى "تدريب" و "تحكم" ، وكذلك ظاهرة مثل إعادة التدريب أو "إعادة تدريب" البيانات. مع التقريب الصحيح ، سيكون لدينا خطأ معين في بيانات التدريب وخطأ أكبر قليلاً في بيانات التحكم. إذا كان هذا خطأ ، فهو يعد ضبطًا دقيقًا لبيانات التدريب وخطأًا كبيرًا في عنصر التحكم.
(من الحقائق المعروفة أنه من خلال نقاط N يمكن رسم منحنى واحد من الدرجة N-1 ، وهذه الطريقة بشكل عام لا تعطي النتيجة المرجوة.
استيفاء لاجرانج متعدد الحدود على ويكيبيديا )
1. وضعنا التوزيع الأولي

2. قسّم النقاط إلى "تدريب" و "تحكم" بنسبة 70 إلى 30.

3. نرسم منحنى تقريبي لنقاط التدريب ، نرى الخطأ الذي يعطيه على بيانات التحكم

4. نرسم المنحنى الدقيق خلال نقاط التدريب ، ونرى خطأً فظيعًا في بيانات التحكم (والصفر في التدريب ، ولكن ما هي النقطة؟).

بالطبع ، يتم عرض المتغير الأبسط مع قسم واحد إلى مجموعات فرعية "تدريب" و "تحكم" ، في الحالة العامة يتم ذلك بشكل متكرر للحصول على أفضل تعديل للمعاملات.
الملف متاح هنا ، فحص مكافحة الفيروسات. قم بتشغيل وحدات الماكرو للعمل بشكل صحيح
3. التدرج النسب وديناميكيات الخطأ
سيكون هناك حالة 4 الأبعاد والانحدار الخطي. سيتم تحديد معاملات الانحدار الخطي في خطوات حسب طريقة النسب التدرج ، في البداية تكون جميع المعاملات صفرا. يوضح الرسم البياني المنفصل ديناميكيات الحد من الأخطاء حيث يتم ضبط المعاملات بشكل متزايد. من الممكن رؤية كل التوقعات ثنائية الأبعاد الأربعة.
إذا قمت بتعيين خطوة نزول التدرج كبيرة جدًا ، فمن الواضح أنه في كل مرة نتخطى الحد الأدنى وسنصل إلى النتيجة بعدد أكبر من الخطوات ، على الرغم من أننا سنأتي في النهاية على أي حال (ما لم نلمس خطوة النزول كثيرًا ، فستنتقل الخوارزمية " في التباعد "). والرسم البياني لاعتماد الخطأ على خطوة التكرار لن يكون سلسًا ، ولكن "متشنج".
1. توليد البيانات ، تعيين خطوة نزول التدرج
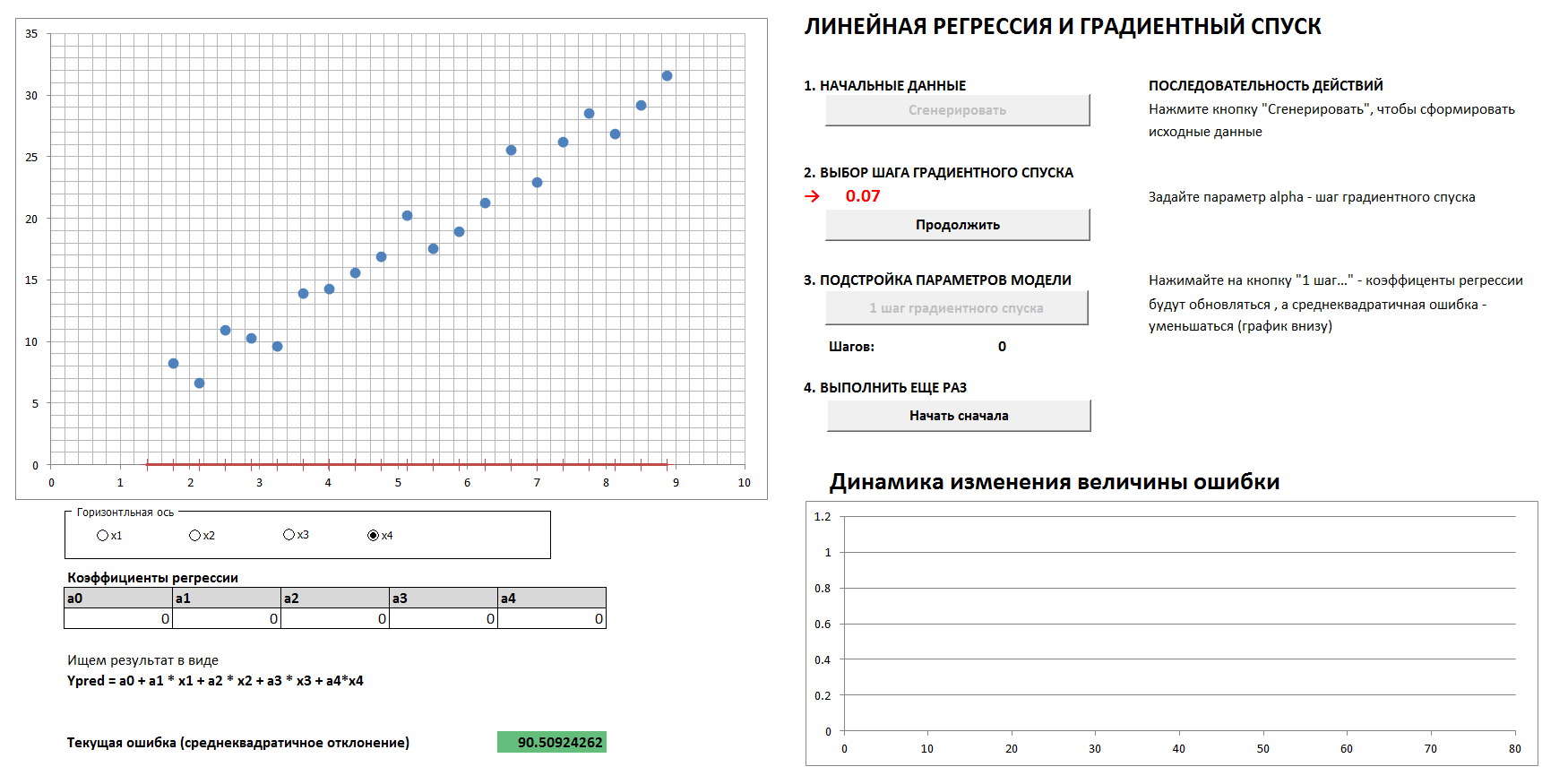
2. مع الاختيار الصحيح لخطوة التدرج اللوني ، نصل إلى الحد الأدنى بسلاسة وسرعة

3. إذا تم تحديد خطوة نزول التدرج بشكل غير صحيح ، فإننا نتخطى الحد الأقصى ، الرسم البياني الخطأ هو "متشنج" ، والتقارب يأخذ عددًا أكبر من الخطوات

و

4. مع التحديد غير الصحيح تمامًا لخطوة الانحدار التدريجي ، نبتعد عن الحد الأدنى

(لإعادة إنتاج العملية بقيم خطوة تدرج النسب الموضحة في الصور ، حدد مربع "البيانات المرجعية").
ملف - من خلال هذا الرابط ، تحتاج إلى تمكين وحدات الماكرو ، لا توجد فيروسات.وفقًا لمجتمع محترم ، هل هذا التبسيط وطريقة التقديم مقبول؟ هل يجب علي ترجمة المقال إلى الإنجليزية؟