الاستخدام العملي لجهاز D-Wave 2000Q: منحنى تعليمي حاد للحوسبة الكمومية

من الصعب إعادة التفكير في مفهوم المهمة ، لكن النتيجة تستحق العناء.

ملاحظة المؤلف : أعلم أنني قمت بشكل غير صحيح باحتساب نقل Bragg في كل من الحالات الكلاسيكية والكمومية ؛ ومع ذلك ، فهو قريب بدرجة كافية من الحقيقة لفهم الفرق بين برمجة أجهزة الكمبيوتر الكلاسيكية والكمومية.

الوقت: في مكان ما في عام 2018. الموقع: قناة فاسدة في سلاكا.

"هل تعرف بايثون؟"

يمكن في بعض الأحيان أن نتفاجأ مع أسئلة جون تيمر ، المدير العلمي لآرس تكنيكا. إذا كان من الممكن تشريب الرسائل في سلاكا بعناية ، فإن إجابتي "نعم" ببساطة ستستجيب معها.

اتضح أن D-Wave قررت منح العالم إمكانية الوصول إلى أداة تحسين الكم الخاصة به من خلال واجهة برمجة التطبيقات. دعاه آرس للمحاولة ، لكنك بحاجة لمعرفة بيثون. كنت على استعداد لذلك.

لقد افترضت أن D-Wave ستصدر نوعًا من واجهة برمجة التطبيقات الرائعة التي يمكن أن تأخذ شفرة الملكية الخاصة بي التي تجعل المبرمجين يبكون ، ويحولونها إلى خطوط محسّنة من الناحية الكمية. للأسف ، عندما وصلت إلى مُحسِّن الكم ، اتضح أنه لم يكن كذلك. لقد وجدت نفسي سريعًا منغمسًا في الوثائق ، محاولًا اكتشاف ما أحتاج إلى فعله على الإطلاق.

أعتقد أن ممثل العلاقات العامة D-Wave كان في ذهنه شخص كان يعرف ما يكفي لوضع أمثلة جاهزة. لكن أنا عنيد. كنت بحاجة إلى الخروج بثلاث أو أربع مهام ممكنة أردت اختبارها. أردت معرفة ذلك: هل يمكنني إتقان عملية حل هذه المشكلات على جهاز كمبيوتر D-Wave؟ ما مدى سهولة القيام قفزة مفاهيمية من البرمجة الكلاسيكية إلى العمل مع التلدين الكمي؟ هل ستناسب بعض مهامي على الأقل هذا الجهاز؟

بالكشف عن استنتاج مدهش على الفور ، سأقول أن الإجابات كانت على النحو التالي: ربما لا يكون "اتقان" تمامًا ؛ صعوبة. ليس كل المهام.

اختيار المهام للبرمجة

على الرغم من الطريقة التي تتخيلني بها ، يمكن أن أطلق علي مبرمج ممارس. في الأساس ، فإن أي شخص لديه فهم جيد للبرمجة سوف يكدح (وربما يرتكب جريمة قتل) بعد رؤية كود بيثون الخاص بي.

ومع ذلك ، يمكنني الخروج بمهام تتطلب كتابة برنامج لحلها. أحتاج ، على سبيل المثال ، إلى شيء يحسب المجال الكهربائي لمجموعة من الأقطاب الكهربائية. شيء يجد الدولة مع الحد الأدنى من طاقة ذرة الهيليوم. أو شيء يحسب الزيادة في شدة الضوء في بداية الليزر. هذه المهام تهمني أكثر. وبدءًا من هذا المشروع ، لم يكن لدي أي فكرة عما إذا كانت بنية D-Wave قادرة على حل هذه المشكلات.

لقد اخترت مشكلتين ، في رأيي ، يمكن أن تنجح: العثور على أعضاء من مجموعة ماندلبروت وحساب معالم محتملة لمجموعة من الأقطاب الكهربائية. كانت ميزة هذه المشكلات هي أنه يمكنني حلها بسرعة باستخدام الكود الكلاسيكي ومقارنة الإجابات. لكنني واجهت بسرعة مشاكل في محاولة لمعرفة كيفية البدء في حل هذه المشاكل على جهاز من D-Wave. يتطلب تحولا كبيرا في فهم المهام ، وتفكيري يعمل بشكل واضح تماما.

على سبيل المثال ، إحدى المشكلات التي واجهتها هي أننا نتعامل مع الأرقام الثنائية ذات المستوى المنخفض (على الرغم من حقيقة أنها يتم التعبير عنها في شكل qubits ، وليس البتات). هذا يعني ، في الواقع ، أن البرنامج لا يحتوي على أنواع. لقد كانت كل تجربة البرمجة تقريبًا لحل المشكلات المادية باستخدام أنواع الفاصلة الرقمية العائمة.

يجب أن تفكر بشكل مختلف في المهمة: يجب التعبير عن الإجابة كرقم ثنائي (مثالي ، صحيح أو خطأ) ، ويجب التعبير عن جميع الفيزياء (على سبيل المثال ، جميع أرقام الفاصلة العائمة) من خلال مجموعة من البتات. حتى لو كانت حياتي تعتمد عليها ، فلن أكون قادرًا على معرفة كيف يمكن القيام بذلك لأي من مهامي. منغمسين في التدريس ، سمحت لهذه المشكلة أن تغلي قليلاً في عصير بلدي.

بعد ستة أشهر ، واجهت أخيرًا مشكلة اعتدت على حلها باستخدام جهاز كمبيوتر D-Wave. يمكن التعبير عن مرور الضوء عبر شبكة صريف Bragg كمشكلة ثنائية: هل خرج فوتون من المرشح أم لا؟ يتم احتواء جميع الفيزياء في المركبات qubit ، ويتم استخراج الجواب من طاقة الحل.

المشابك براج

مقضب Bragg أحادي البعد هو مادة متعددة الطبقات. كل فجوة بين الطبقتين تعكس كمية صغيرة من الضوء. يتم تحديد الاختراق الكلي خلال الهيكل بأكمله من خلال المسافة بين الثغرات. حتى يمر الضوء ، من الضروري أن تضيف الموجات من فواصل زمنية مختلفة مرحلة. يظهر أدناه الطيف التمثيلي لشبكة Bragg المثالية ذات 50 طبقة وانعكاس بنسبة 0.1٪.



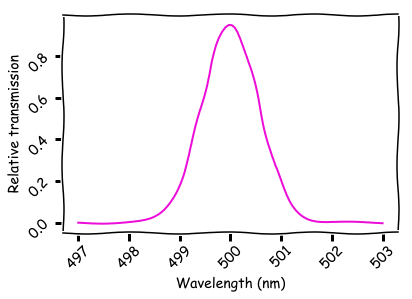
تقوم التعليمة البرمجية التالية بإنشاء بيانات لهذا الرسم البياني:

ld = np.linspace(ld_center-3e-9, ld_center+3e-9, num_ld) k = 2*np.pi/ld T = np.ones(ld.shape) for j in range(num_layers): T = T*(1-A)*np.cos(j*k*layer_sep)**2 

هنا نحسب بشكل صريح المساهمات النسبية لكل فجوة ، معبراً عنها بالقدرة البصرية ، والتي تصل إلى الفجوة التالية. يؤخذ التداخل البناء والمدمّر في الاعتبار عن طريق تقليل أو زيادة مساهمة الفجوة ، وهذا يتوقف على مدى قرب المسافة بين الطبقات التي تتزامن مع نصف طول الموجة.

يعد هذا الاختراق ضروريًا لأنه يتم التعبير عن اتصال الكيبيتات بالأرقام الحقيقية فقط وليس بالأعداد المركبة (يتم التعبير عن الفيزياء بشكل أفضل من خلال الأعداد المركبة التي تحتوي على سعة ومرحلة الضوء). ومع ذلك ، يبدو إخراج الكود الكلاسيكي صحيحًا تقريبًا - عدم وجود نطاقات تردد جانبي تقلق قليلاً ، مما يشير إلى عدم اكتمال النموذج ، ولكن لا يهم حتى الآن.

رمز النموذج الكلاسيكي يفتقر إلى اختبارات التناسق. حسبتُ النتيجة ، موضحةً بالضبط كيف ستنتشر الموجة. حتى إذا تبين أن هذا الافتراض غير صحيح ، فإن نتيجة الحساب ستكون هي نفسها - على الرغم من أن جميع المعادلات تعتمد على الفيزياء ، إلا أنه من المستحيل ضمان في الكود الذي تصفه بشكل صحيح.

نمر إلى الكوانتا

في نظام D-Wave ، من الضروري إنشاء سلسلة من البتات ، يمثل كل منها شدة الضوء في الفجوة. يرتبط كل كيلو بايت بجيرانه ، ويمثل وزن الاتصال مرورًا من فجوة إلى أخرى ، مع مراعاة المسافة بين الواجهات. إذا كانت المسافة بين الواجهات تساوي نصف الطول الموجي ، يمكن للضوء أن يتردد صداها بين الواجهتين ويمرر. إذا كانت المسافة ربع الطول الموجي ، يتم تشغيل التداخل المدمر ، ويجب أن يكون الاتصال ضئيلًا.

يشار إلى المرور من خلال فجوة واحدة في 99.9 ٪ ، وبالتالي فإن العلاقة بين صفر وأول بايت

$$

$$P_ {0،1} = 0،999 cos ^ 2 (2 \ pi d / \ lambda)$$

بين الأول والثاني:

$$

$$P_ {1،2} = P_ {0،1} 0،999 cos ^ 2 (4 \ pi d / \ lambda)$$

بين الثاني والثالث:

$$

$$P_ {2،3} = P_ {1،2} P_ {0،1} 0،999 cos ^ 2 (6 \ pi d / \ lambda)$$

في هذه الصيغة ، d هي المسافة المادية بين الطبقات ، و λ هي الطول الموجي. إذا كان d / λ = 0.5 ، فإن جيب التمام يساوي الوحدة ، ويمكننا أن نأمل في انتقال مثالي للضوء.

في نظام D-Wave ، هذا يعني أنه يجب توصيل كل اثنين من وحدات البت المجاورة على النحو التالي:

$$

$$P_ {i، j} = [0،999 cos ^ 2 (2i \ pi d / \ lambda)] ^ i$$

في هذا التعبير ، تأخذ الدرجة u في الاعتبار تأثير البتات السابقة وتبسط نظام الاتصال.

تنفيذ المهمة

الآن ، ومعرفة كيفية توصيل وحدات البت ، يجب أن ننظر إلى التوصيل الفعلي للبتات لتحديد كيفية إكمال هذه المهمة. وهذا ما يسمى التضمين طفيفة.

يجب أن نعطي الكمبيوتر قائمة بالاتصالات بين البتات مع أوزانها. يجب علينا أيضا تحديد الانحرافات التي تشير إلى أهمية كل qubit. في حالتنا ، تكون جميع الكيبيتات متساوية في الأهمية ، وبالتالي يتم ضبطها على أنها -1 لجميع البتات (أخذت هذا الرقم من المثال القياسي). يجب أن ترتبط الانحرافات والروابط بالبتات المادية والعلاقات بينهما. في حالة المهام الكبيرة ، قد يستغرق البحث عن مثل هذا التعيين وقتًا طويلاً.

رمز توليد العلاقات والانحرافات بسيط للغاية.

  #qubit labels (q[j], q[j])       linear.update({(q[j], q[j]): -1}) #   #     if jk == -1: quad.update({(q[j], q[k]): (J_vals[j])**k}) #    else: quad.update({(q[j], q[k]): 0}) 

لحسن الحظ ، ستحاول واجهة برمجة تطبيقات D-Wave العثور على تطبيق صغير من تلقاء نفسها. لقد وجدت أنها تعمل لمرشح يحتوي على 50 طبقة ، لكن لا يمكنني التعامل مع 100 طبقة. هذا يبدو غريباً بالنسبة لي ، نظرًا لوجود 2000 كيلو بايت وطول السلسلة 1 (لا نحتاج إلى الجمع بين عدة وحدات فعلية لإنشاء واحد منطقي) ، يجب أن يكون النظام قادرًا على تنفيذ مشكلات أكبر. إذا نظرنا إلى الوراء ، أعتقد أن الفشل كان بسبب حقيقة أنني طلبت الكثير من الاتصالات صفر.

النهج البديل هو ببساطة عدم تحديد الروابط الفارغة بشكل صريح. يمنح هذا الخوارزمية حرية البحث عن المزيد من خيارات التنفيذ حيث لا توجد روابط على الكيبيتات. لم أحاول هذا ، لكن هذا الخيار يبدو لي الخطوة المنطقية التالية.

في أي حال ، فإن بدء تشغيل جهاز D-Wave بسيط للغاية:

 response = EmbeddingComposite(DWaveSampler()).sample_qubo(Q_auto, num_reads=num_runs) 

تعلم التحدث بشبهة

الفرق بين الخوارزمية الكلاسيكية وحل D-Wave هو أن كمبيوتر D-Wave لا يُرجع مباشرة نتيجة واضحة. اتضح كسر في أجزاء كثيرة. لدينا قائمة من الطاقات ، وأصغرها يجب أن يكون هو الحل. بالنسبة لعدة مرات تشغيل (مثل 1000) لكل طاقة ، نحصل على عدد المرات التي ظهرت بها في الإجابة. ولكل مرة نحصل على "استجابة" ، قيمة البتات. لم يكن واضحا على الفور بالنسبة لي أي من هذه القيم يمكن (ويمكن) أن تفسر على أنها تمر عبر مرشح.

في النهاية ، قررت أن الحد الأدنى للطاقة الحل سيكون أفضل إجابة ، لأن هذه القيمة تمثل إلى حد ما كمية الطاقة المخزنة في المرشح. لذلك ، يمثل الحل ذو الطاقة الأعلى نفاذية أكبر للمرشح ، كما هو موضح أدناه. يتم ترك تحويل هذه الإجابة إلى مسار حقيقي للضوء كواجب منزلي لأولئك الذين يفهمون هذا.



من الممكن أيضًا الحصول على تمثيل مادي للعملية من خلال فحص قيم البتات في حل بأقل طاقة. فيما يلي يمكنك رؤية قيم بت الحلول التي تتوافق مع ذروة منحنى الإرسال (500 نانومتر) ، 50٪ الإرسال (500.6 نانومتر) والإرسال 5٪ (501.4 نانومتر).



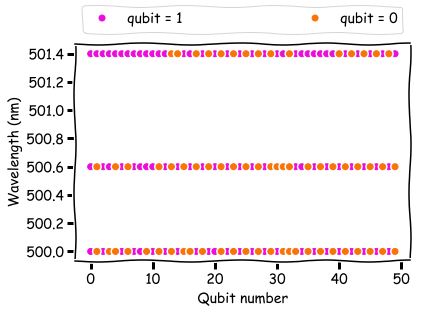
عند حافة ذروة الإرسال ، تميل البتات إلى التراكم في مجموعات من الوحدات. في الذروة ، تتناوب البتات بين 0 و 1. هذا الحل الأخير هو صورة ثنائية لكيفية تباين شدة الضوء في مقضب Bragg. بمعنى آخر ، يقدم حل D-Wave أيضًا الفيزياء مباشرةً ، والتي لا يمكن قولها عن الكود الكلاسيكي.

هذه هي القوة الحقيقية للصلب الكمي. نعم ، يمكنني استخلاص منحنى المرور عبر المرشح من الحسابات الكلاسيكية. ولكن للحصول على صورة لما يحدث بالفعل في الداخل ، فإنك تحتاج إلى رمز أكثر تعقيدًا. وفي التلدين الكمي ، هذا مجاني تمامًا. في رأيي ، هذا رائع جدا.

ميزة أخرى للتليين الكمي هي أنه يضمن حلاً ثابتًا في إطار خياري لأوزان السندات qubit. هذا يعني أن حل الكمبيوتر الكمومي من المرجح أن يكون أكثر موثوقية من الحل الذي تم الحصول عليه من التعليمات البرمجية الكلاسيكية.

مناقشات حول البرمجة الكمومية

الجزء الأصعب في برمجة جهاز D-Wave هو أنك تحتاج إلى التفكير بشكل مختلف في المهام. على سبيل المثال ، اعتدت على التقليل من المشاكل عندما يتزامن المنحنى مع البيانات. لكنني وجدت صعوبة بالغة في تغيير طريقة تفكيرك في مشكلة جسدية بحيث تبدأ في كتابة التعليمات البرمجية لحلها. لا يساعد ذلك في أن تبدو معظم الأمثلة التي قدمتها الشركة مجردة وغير قابلة للتكيف مع المشاكل المادية بالنسبة لي. ولكن هذا الموقف سيتغير عندما يبدأ عدد متزايد من المستخدمين في نشر التعليمات البرمجية الخاصة بهم.

أيضا ، قد تنشأ صعوبات مع تفسير الجواب. في الأساس ، أحببت بساطة واجهة برمجة التطبيقات ، ومن الرائع الحصول على أفكار إضافية مجانًا. في المستقبل القريب ، يمكنني استخدام D-Wave لحل المشاكل الحقيقية.