هياكل البيانات الغريبة: تعديل ميركل باتريشيا تري

"ما نوع الشيطان الذي يجب أن أتذكره بكل صواب هذه الخوارزميات اللعينة وهياكل البيانات؟"

حول هذا يأتي إلى تعليقات معظم المقالات حول مرور المقابلات الفنية. الأطروحة الرئيسية ، كقاعدة عامة ، هي أن كل ما يتم استخدامه بطريقة أو بأخرى قد تم تنفيذه بالفعل عشر مرات وأنه من غير المرجح أن يتعامل هذا المبرمج العادي. حسنا ، هذا صحيح إلى حد ما. ولكن ، كما اتضح فيما بعد ، لم يتم تنفيذ كل شيء ، وما زلت ، لسوء الحظ (أو لحسن الحظ؟) لا يزال يتعين علي إنشاء بنية بيانات.

الغامضة المعدلة ميركل باتريشيا تري.

نظرًا لعدم وجود معلومات حول هذه الشجرة على الإطلاق ، وفي المتوسط ​​- أكثر قليلاً ، أريد أن أخبركم بنوع الحيوان الذي يتم تناوله وما الذي يتم تناوله به.

ما هذا

إخلاء المسئولية: كان المصدر الرئيسي للمعلومات الخاصة بالتنفيذ بالنسبة لي هو الورقة الصفراء ، بالإضافة إلى شفرات مصدر التكافؤ - ethereum و go-ethereum . كان هناك حد أدنى من المعلومات النظرية حول تبرير بعض القرارات ، لذلك فإن كل الاستنتاجات حول أسباب اتخاذ قرارات معينة هي بياناتي الشخصية. في حال كنت مخطئًا في شيء ما - سأكون سعيدًا بتصويبات في التعليقات.

الشجرة هي بنية بيانات عبارة عن رسم بياني مترابط متصل. كل شيء بسيط هنا ، والجميع على دراية بهذا.

شجرة البادئة هي شجرة الجذر التي يمكن تخزين أزواج قيمة المفتاح فيها بسبب تقسيم العقد إلى نوعين: تلك التي تحتوي على جزء من المسار (بادئة) ، وعقد الأوراق التي تحتوي على القيمة المخزنة. توجد قيمة في شجرة إذا وفقط ، باستخدام المفتاح ، يمكننا الانتقال من جذر الشجرة والعثور على عقدة ذات قيمة في النهاية.

شجرة PATRICIA هي شجرة بادئة تكون فيها البادئات ثنائية - أي أن كل عقدة رئيسية تخزن معلومات حول بت واحد.

شجرة Merkle هي شجرة تجزئة مبنية على نوع من سلسلة البيانات ، تجمع هذه الرموز نفسها في واحد (الجذر) ، وتخزين المعلومات حول حالة جميع كتل البيانات. أي أن تجزئة الجذر هي نوع من "التوقيع الرقمي" لحالة سلسلة الكتل. يستخدم هذا الشيء بنشاط في blockchain ، ويمكن الاطلاع على المزيد حول هذا الموضوع هنا .

المجموع: تم تعديل Merkle Patricia Trie (المشار إليها فيما يلي باسم MPT باختصار) وهي عبارة عن شجرة تجزئة تقوم بتخزين أزواج القيمة الرئيسية ، ويتم تقديم المفاتيح في شكل ثنائي. وما هو بالضبط "التعديل" ، سنكتشف لاحقًا بعض الشيء عندما نناقش التنفيذ.

لماذا هذا؟

يستخدم MPT في مشروع Ethereum لتخزين البيانات المتعلقة بالحسابات والمعاملات ونتائج تنفيذها والبيانات الأخرى اللازمة لتشغيل النظام.
على عكس Bitcoin ، حيث تكون الحالة ضمنية ويتم حسابها بواسطة كل عقدة بشكل مستقل ، يتم تخزين رصيد كل حساب (بالإضافة إلى البيانات المرتبطة به) مباشرةً على blockchain على الهواء. علاوة على ذلك ، يجب توفير موقع البيانات وقابليتها للتشفير - سيستخدم عدد قليل من الأشخاص العملة المشفرة التي يمكن أن يتغير فيها رصيد الحساب العشوائي دون أسباب موضوعية.

تتمثل المشكلة الرئيسية التي يواجهها مطورو Ethereum في إنشاء بنية بيانات تتيح لك تخزين أزواج قيمة المفتاح بشكل فعال وفي نفس الوقت توفير التحقق من البيانات المخزنة. لذلك ظهرت MPT.

كيف هذا؟

MPT عبارة عن شجرة PATRICIA بادئة حيث تكون المفاتيح تسلسلات بايت.

الحواف في هذه الشجرة عبارة عن تسلسل nibble (نصف بايت). وفقًا لذلك ، يمكن أن تحتوي العقدة الواحدة على ستة عشر منحدرة (تقابل الفروع من 0x0 إلى 0xF).

وتنقسم العقد إلى 3 أنواع:

• العقدة الفرعية. العقدة المستخدمة للتفرع. يحتوي على ما يصل إلى 1 إلى 16 رابطًا إلى العقد الفرعية. قد تحتوي أيضًا على قيمة.
• عقدة التمديد. العقدة المساعدة التي تخزن جزءًا من المسار المشترك للعديد من العقد الفرعية ، بالإضافة إلى ارتباط إلى العقدة الفرعية الموجودة أدناه.
• عقدة ورقة. عقدة تحتوي على جزء من المسار والقيمة المخزنة. إنها النهاية في السلسلة.

كما ذكرنا سابقًا ، تم بناء MPT أعلى مستودع kv آخر ، والذي يخزن العقد في شكل "link" => " RLP encoded node".

وهنا نأتي بمفهوم جديد: RLP. باختصار ، هذه طريقة لترميز البيانات التي تمثل قوائم أو تسلسلات البايت. مثال: [ "cat", "dog" ] = [ 0xc8, 0x83, 'c', 'a', 't', 0x83, 'd', 'o', 'g' ] . لن أخوض في التفاصيل على وجه الخصوص ، وفي التطبيق أستخدم مكتبة جاهزة ، لأن تغطية هذا الموضوع أيضًا ستؤدي إلى تضخيم مقال كبير بالفعل. إذا كنت لا تزال مهتمًا ، يمكنك قراءة المزيد هنا . نحن نقتصر على حقيقة أنه يمكننا تشفير البيانات في RLP وفك تشفيرها مرة أخرى.

يتم تعريف ارتباط العقدة على النحو التالي: إذا كان طول العقدة المشفرة RLP هو 32 بايت أو أكثر ، فإن الارتباط هو تجزئة keccak من تمثيل RLP للعقدة. إذا كان الطول أقل من 32 بايت ، فإن الارتباط هو تمثيل RLP للعقدة نفسها.

من الواضح ، في الحالة الثانية ، لا تحتاج إلى حفظ العقدة في قاعدة البيانات ، لأنه سيتم حفظه بالكامل داخل العقدة الأصل.

يتيح لك الجمع بين ثلاثة أنواع من العقد تخزين البيانات بشكل فعال في الحالة عندما يكون هناك عدد قليل من المفاتيح (عندئذٍ سيتم تخزين معظم المسارات في امتدادات وعقد أوراق ، وسيكون هناك عدد قليل من العقد الفرعية) ، وفي حالة وجود العديد من العقد (لن يتم تخزين المسارات بشكل صريح ، لكنهم "سيتجمعون" أثناء المرور عبر العقد الفرعية).

مثال كامل لشجرة باستخدام جميع أنواع العقد:

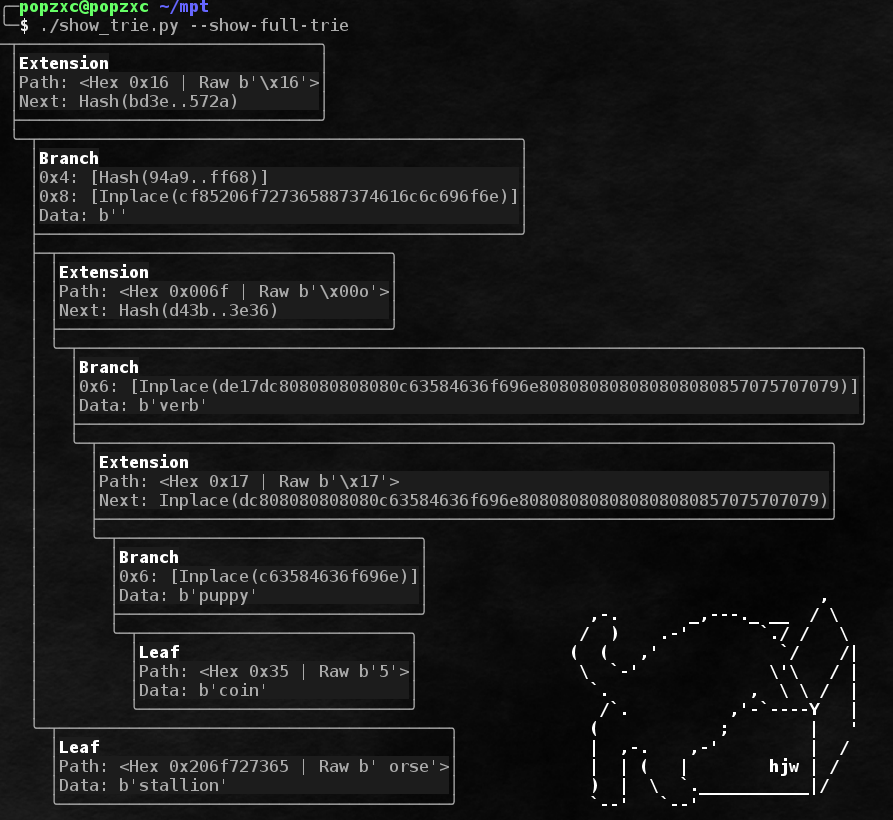
كما قد تلاحظ ، فإن الأجزاء المخزنة في المسارات لها بادئات. البادئات مطلوبة لعدة أغراض:

1. لتمييز العقد التمديد من العقد ورقة.
2. لمحاذاة تسلسل عدد فردي من القضم.

قواعد إنشاء البادئات بسيطة جدًا:

• البادئة تأخذ 1 nibble. إذا كان طول المسار (باستثناء البادئة) غريبًا ، فسيبدأ المسار فورًا بعد البادئة. إذا كان طول المسار متساويًا ، فيتم محاذاة بعد البادئة ، تتم إضافة nibble 0x0 أولاً.
• البادئة هي في البداية 0x0.
• إذا كان طول المسار غريبًا ، فسيتم إضافة 0x1 إلى البادئة ، حتى لو - 0x0.
• إذا كان المسار يؤدي إلى عقدة Leaf ، فسيتم إضافة 0x2 إلى البادئة ، إذا تم إضافة 0x0 إلى عقدة Extension.

على beatiks ، أعتقد ، سيكون أكثر وضوحا:

 0b0000 =>  , Extension  0b0001 =>  , Extension  0b0010 =>  , Leaf  0b0011 =>  , Leaf  

إزالة ليست إزالة

على الرغم من حقيقة أن الشجرة لديها عملية حذف العقد ، في الواقع ، يبقى كل شيء تمت إضافته في الشجرة إلى الأبد.

يعد هذا ضروريًا من أجل عدم إنشاء شجرة كاملة لكل كتلة ، ولكن لتخزين الفرق بين الإصدارات القديمة والجديدة فقط من الشجرة.

وفقًا لذلك ، باستخدام تجزئة الجذر المختلفة كنقطة دخول ، يمكننا الحصول على أي من الحالات التي كانت الشجرة موجودة فيها.

هذه ليست كل التحسينات. هناك الكثير ، لكننا لن نتحدث عن ذلك - وبالتالي فإن المقال كبير. ومع ذلك ، يمكنك أن تقرأ لنفسك.

تطبيق

انتهت النظرية ، دعنا ننتقل إلى الممارسة. سوف نستخدم لغة مشتركة من عالم تكنولوجيا المعلومات ، وهذا هو python .

نظرًا لأنه سيكون هناك الكثير من التعليمات البرمجية ، ولتنسيق المقالة ، يجب تخفيض الكثير وتقسيمه ، سأترك رابطًا إلى github على الفور.
إذا لزم الأمر ، هناك يمكنك أن ترى الصورة كاملة.

أولاً ، نحدد واجهة الشجرة التي نريد الحصول عليها كنتيجة:

 class MerklePatriciaTrie: def __init__(self, storage, root=None): pass def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass 

الواجهة بسيطة للغاية. العمليات المتوفرة هي الحصول على وحذف وإدراج وتغيير (مجتمعة في التحديث) ، وكذلك الحصول على تجزئة الجذر.

سيتم نقل التخزين إلى طريقة __init__ - وهي بنية تشبه البيانات التي سنقوم بتخزين العقد بها ، وكذلك root - "الجزء العلوي" من الشجرة. إذا تم تمرير None root ، فإننا نفترض أن الشجرة فارغة وتعمل من الصفر.

_Remark: قد تتساءل عن سبب تسمية المتغيرات في الأساليب باسم encoded_key و encoded_value ، وليس فقط key / value . الإجابة بسيطة: وفقًا للمواصفات ، يجب تشفير جميع المفاتيح والقيم في RLP . لن نزعج أنفسنا في هذا الأمر ونترك هذا الاحتلال على أكتاف مستخدمي المكتبة.

ومع ذلك ، قبل البدء في تنفيذ الشجرة نفسها ، يجب القيام بأمرين مهمين:

1. قم NibblePath فئة NibblePath ، وهي سلسلة من nibbles ، حتى لا يتم ترميزها يدويًا.
2. لتنفيذ فئة Node في إطار هذه الفئة - Extension ، Leaf Branch .

NibblePath

لذلك ، NibblePath . نظرًا لأننا سننتقل بنشاط حول الشجرة ، يجب أن تكون أساس وظيفة صفنا هي القدرة على تعيين "الإزاحة" من بداية المسار ، وكذلك تلقي حلمة محددة. مع العلم بذلك ، فإننا نحدد أساس فئتنا (وكذلك بعض الثوابت المفيدة للعمل مع البادئات أدناه):

 class NibblePath: ODD_FLAG = 0x10 LEAF_FLAG = 0x20 def __init__(self, data, offset=0): self._data = data # ,   . self._offset = offset #      def consume(self, amount): # "" N      . self._offset += amount return self def at(self, idx): #      idx = idx + self._offset #    ,   ,    , #   ,    -      . byte_idx = idx // 2 nibble_idx = idx % 2 #   . byte = self._data[byte_idx] #      . nibble = byte >> 4 if nibble_idx == 0 else byte & 0x0F return nibble 

بسيط للغاية ، أليس كذلك؟

يبقى لكتابة وظائف فقط لترميز وفك تشفير سلسلة من يقضم.

 class NibblePath: # ... def decode_with_type(data): #   : # ,     ,    . is_odd_len = data[0] & NibblePath.ODD_FLAG == NibblePath.ODD_FLAG is_leaf = data[0] & NibblePath.LEAF_FLAG == NibblePath.LEAF_FLAG #    ,     #    . offset  , #       "" . offset = 1 if is_odd_len else 2 return NibblePath(data, offset), is_leaf def encode(self, is_leaf): output = [] #    ,       . nibbles_len = len(self._data) * 2 - self._offset is_odd = nibbles_len % 2 == 1 #  . prefix = 0x00 #    ,    . #      (self.at(0))     . #           (0x0). prefix += self.ODD_FLAG + self.at(0) if is_odd else 0x00 #  ,  Leaf node,  . prefix += self.LEAF_FLAG if is_leaf else 0x00 output.append(prefix) # ,      ,  . pos = nibbles_len % 2 #          , #     2 ,    , #     , #    . while pos < nibbles_len: byte = self.at(pos) * 16 + self.at(pos + 1) output.append(byte) pos += 2 return bytes(output) 

من حيث المبدأ ، وهذا هو الحد الأدنى الضروري للعمل مريحة مع يقضم. بالطبع ، في التطبيق الحالي ، لا يزال هناك عدد من الأساليب المساعدة (مثل combine ، ودمج مسارين في واحد) ، ولكن تنفيذها تافه للغاية. إذا كانت مهتمة ، يمكن العثور على النسخة الكاملة هنا .

العقدة

كما نعلم بالفعل ، يتم تقسيم العقد لدينا إلى ثلاثة أنواع: أوراق ، تمديد وفرع. يمكن تشفيرها وفك تشفيرها جميعًا ، والفرق الوحيد هو البيانات المخزنة داخلها. لكي نكون صادقين ، هذا هو ما تطلبه أنواع البيانات الجبرية ، وفي Rust ، على سبيل المثال ، أود أن أكتب شيئًا بالروح:

 pub enum Node<'a> { Leaf(NibblesSlice<'a>, &'a [u8]), Extension(NibblesSlice<'a>, NodeReference), Branch([Option<NodeReference>; 16], Option<&'a [u8]>), } 

ومع ذلك ، لا يوجد ADT في الثعبان على هذا النحو ، لذلك سوف نحدد فئة Node ، وداخلها هناك ثلاث فئات المقابلة لأنواع العقدة. نحن ننفذ الترميز مباشرة في فئات العقدة ، ونفك التشفير في فئة Node .

التنفيذ ، مع ذلك ، أساسي:

ورقة:

 class Leaf: def __init__(self, path, data): self.path = path self.data = data def encode(self): #    --    , #   -  ,   -  . return rlp.encode([self.path.encode(True), self.data]) 

التمديد:

 class Extension: def __init__(self, path, next_ref): self.path = path self.next_ref = next_ref def encode(self): #    --    , #   -  ,   -    . next_ref = _prepare_reference_for_encoding(self.next_ref) return rlp.encode([self.path.encode(False), next_ref]) 

الفرع:

 class Branch: def __init__(self, branches, data=None): self.branches = branches self.data = data def encode(self): #    --    ,  #  16 -     (  ), #   -   (  ). branches = list(map(_prepare_reference_for_encoding, self.branches)) return rlp.encode(branches + [self.data]) 

كل شيء بسيط جدا. الشيء الوحيد الذي قد يسبب أسئلة هو وظيفة _prepare_reference_for_encoding .

ثم أعترف ، كان علي استخدام عكاز صغير. والحقيقة هي أن مكتبة rlp تقوم rlp البيانات بشكل متكرر ، ويمكن أن يكون الارتباط إلى عقدة أخرى ، كما نعلم ، rlp بيانات rlp (في حالة أن تكون العقدة المشفرة أقل من 32 حرفًا). العمل مع روابط بتنسيقين - بايت التجزئة وعقدة فك الشفرة - غير مريح للغاية. لذلك ، كتبت وظيفتين ، بعد فك تشفير العقدة ، قم بإرجاع الارتباطات بتنسيق بايت ، وفك تشفيرها إذا لزم الأمر ، قبل الحفظ. هذه الوظائف هي:

 def _prepare_reference_for_encoding(ref): #    ( ,   ) --  . #       :) if 0 < len(ref) < 32: return rlp.decode(ref) return ref def _prepare_reference_for_usage(ref): #     -   . #          . if isinstance(ref, list): return rlp.encode(ref) return ref 

مع الانتهاء من العقد عن طريق كتابة فئة Node . ستكون هناك طريقتان فقط: فك شفرة العقدة وتحويل العقدة إلى رابط.

 class Node: # class Leaf(...) # class Extension(...) # class Branch(...) def decode(encoded_data): data = rlp.decode(encoded_data) # 17  -  Branch . if len(data) == 17: branches = list(map(_prepare_reference_for_usage, data[:16])) node_data = data[16] return Node.Branch(branches, node_data) #    17,   2.   - . #      ,     . path, is_leaf = NibblePath.decode_with_type(data[0]) if is_leaf: return Node.Leaf(path, data[1]) else: ref = _prepare_reference_for_usage(data[1]) return Node.Extension(path, ref) def into_reference(node): #    . #      32 , #   -   . #       . encoded_node = node.encode() if len(encoded_node) < 32: return encoded_node else: return keccak_hash(encoded_node) 

استراحة

تفو! هناك الكثير من المعلومات. أعتقد أنه حان الوقت للاسترخاء. هنا قطة أخرى لك:

ميلوتا ، أليس كذلك؟ حسنًا ، عد إلى أشجارنا.

MerklePatriciaTrie

يا هلا - العناصر المساعدة جاهزة ، ونحن نمر إلى أكثر لذيذ. فقط في حالة ، سأذكر واجهة الشجرة الخاصة بنا. في الوقت نفسه ، نطبق طريقة __init__ .

 class MerklePatriciaTrie: def __init__(self, storage, root=None): self._storage = storage self._root = root def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass 

ولكن مع الأساليب المتبقية سنتعامل واحدة تلو الأخرى.

الحصول على

تتكون طريقة get (مثل ، من حيث المبدأ ، الطرق الأخرى) من جزأين. ستقوم الطريقة نفسها بإعداد البيانات وإحضار النتيجة إلى النموذج المتوقع ، في حين سيحدث العمل الحقيقي داخل الطريقة المساعدة.

الطريقة الأساسية بسيطة للغاية:

 class MerklePatriciaTrie: # ... def get(self, encoded_key): if not self._root: raise KeyError path = NibblePath(encoded_key) #       #  ,    ,    . result_node = self._get(self._root, path) if type(result_node) is Node.Extension or len(result_node.data) == 0: raise KeyError return result_node.data 

ومع ذلك ، _get ليس أكثر تعقيدًا: من أجل الوصول إلى العقدة المطلوبة ، نحتاج إلى الانتقال من الجذر إلى المسار المقدم بأكمله. إذا وجدنا في النهاية عقدة تحتوي على بيانات (ورقة أو فرع) - يا هلا ، يتم استلام البيانات. إذا لم يكن من الممكن المرور ، فإن المفتاح المطلوب مفقود في الشجرة.

التنفيذ:

 class MerklePatriciaTrie: # ... def _get(self, node_ref, path): #      . node = self._get_node(node_ref) #    --   . #   ,      . if len(path) == 0: return node if type(node) is Node.Leaf: #     Leaf-,     , #      . if node.path == path: return node elif type(node) is Node.Extension: #    -- Extension,    . if path.starts_with(node.path): rest_path = path.consume(len(node.path)) return self._get(node.next_ref, rest_path) elif type(node) is Node.Branch: #    -- Branch,     . #   ,           #  :      . branch = node.branches[path.at(0)] if len(branch) > 0: return self._get(branch, path.consume(1)) #    ,        , #     . raise KeyError 

حسنًا ، في نفس الوقت ، سنكتب طرقًا لحفظ العقد وتحميلها. إنها بسيطة:

 class MerklePatriciaTrie: # ... def _get_node(self, node_ref): raw_node = None if len(node_ref) == 32: raw_node = self._storage[node_ref] else: raw_node = node_ref return Node.decode(raw_node) def _store_node(self, node): reference = Node.into_reference(node) if len(reference) == 32: self._storage[reference] = node.encode() return reference 

تحديث

طريقة update بالفعل أكثر إثارة للاهتمام. فقط انتقل إلى النهاية وإدراج عقدة Leaf لن تعمل دائمًا. من المحتمل أن تكون نقطة الفصل الرئيسية في مكان ما داخل عقدة Leaf أو Extension المحفوظة بالفعل. في هذه الحالة ، سيكون عليك فصلها وإنشاء عدة عقد جديدة.

بشكل عام ، يمكن وصف كل المنطق بالقواعد التالية:

1. بينما يتزامن المسار تمامًا مع العقد الحالية ، فإننا ننزل الشجرة بشكل متكرر.
2. إذا تم الانتهاء من المسار وتواجدنا في العقدة Branch أو Leaf ، فهذا يعني أن update ببساطة بتحديث القيمة المقابلة لهذا المفتاح.
3. إذا كانت المسارات مقسمة (أي أننا لا نقوم بتحديث القيمة ، ولكننا ندرج واحدة جديدة) ، ونحن في العقدة الفرعية ، نقوم بإنشاء عقدة Leaf وتحديد رابط لها في فرع الفرع المقابل.
4. إذا تم تقسيم المسارات ونحن في عقدة Leaf أو Extension ، نحتاج إلى إنشاء عقدة فرع تفصل بين المسارات ، وإذا لزم الأمر ، فإن عقدة Extension للجزء المشترك من المسار.

دعنا نعبر تدريجيا عن هذا في الكود. لماذا تدريجيا؟ لأن الطريقة كبيرة وسيكون من الصعب فهمها بكميات كبيرة.
ومع ذلك ، سأترك رابطًا للطريقة الكاملة هنا .

 class MerklePatriciaTrie: # ... def update(self, encoded_key, encoded_value): path = NibblePath(encoded_key) result = self._update(self._root, path, encoded_value) self._root = result def _update(self, node_ref, path, value): #       (,   ), #       . if not node_ref: return self._store_node(Node.Leaf(path, value)) #          #    . node = self._get_node(node_ref) if type(node) == Node.Leaf: ... elif type(node) == Node.Extension: ... elif type(node) == Node.Branch: ... 

ليس هناك ما يكفي من المنطق العام ، كل ما هو أكثر إثارة للاهتمام هو داخل if ق.

if type(node) == Node.Leaf

أولاً ، دعنا نتعامل مع عقد Leaf. سيناريوهان فقط ممكنان:

1. ما تبقى من المسار الذي نتبعه هو بالضبط نفس المسار المخزن في عقدة Leaf. في هذه الحالة ، نحتاج فقط إلى تغيير القيمة وحفظ العقدة الجديدة وإرجاع رابط إليها.

   
   

2. المسارات مختلفة.
   في هذه الحالة ، تحتاج إلى إنشاء عقدة فرع تفصل بين المسارين.
   إذا كان أحد المسارات فارغًا ، فسيتم نقل قيمته مباشرةً إلى العقدة الفرعية.
   وإلا ، فسيتعين علينا إنشاء عقدتين للورق تقصرهما طول الجزء المشترك من المسارات + 1 nibble (سيتم الإشارة إلى هذه nibble بواسطة فهرس الفرع المقابل من العقدة الفرعية).

   
   

ستحتاج أيضًا إلى التحقق مما إذا كان هناك جزء مشترك من المسار لفهم ما إذا كنا بحاجة إلى إنشاء عقدة ملحق أيضًا.

في الكود ، سيبدو كما يلي:

 if type(node) == Node.Leaf: if node.path == path: #  .       . node.data = value return self._store_node(node) #    . #    . common_prefix = path.common_prefix(node.path) #      . path.consume(len(common_prefix)) node.path.consume(len(common_prefix)) #  Branch . branch_reference = self._create_branch_node(path, value, node.path, node.data) # ,    Extension-. if len(common_prefix) != 0: return self._store_node(Node.Extension(common_prefix, branch_reference)) else: return branch_reference 

الإجراء _create_branch_node كالتالي:

 def _create_branch_node(self, path_a, value_a, path_b, value_b): #    Branch-. branches = [b''] * 16 # ,     Branch- . branch_value = b'' if len(path_a) == 0: branch_value = value_a elif len(path_b) == 0: branch_value = value_b #    Leaf-,  . self._create_branch_leaf(path_a, value_a, branches) self._create_branch_leaf(path_b, value_b, branches) #  Branch-     . return self._store_node(Node.Branch(branches, branch_value)) def _create_branch_leaf(self, path, value, branches): # ,     Leaf-. if len(path) > 0: #    ( ). idx = path.at(0) #  Leaf-   ,     . leaf_ref = self._store_node(Node.Leaf(path.consume(1), value)) branches[idx] = leaf_ref 

if type(node) == Node.Extension

في حالة عقدة الامتداد ، كل شيء يشبه عقدة Leaf.

1. إذا كان المسار من عقدة الامتداد يمثل بادئة لمسارنا ، فنحن نواصل السير بشكل متكرر.

   
   

2. خلاف ذلك ، نحن بحاجة إلى القيام بالفصل باستخدام عقدة الفرع ، كما في الحالة الموضحة أعلاه.

   
   

وفقا لذلك ، الكود:

 elif type(node) == Node.Extension: if path.starts_with(node.path): #         . new_reference = \ self._update(node.next_ref, path.consume(len(node.path)), value) return self._store_node(Node.Extension(node.path, new_reference)) #  Extension-. #     . common_prefix = path.common_prefix(node.path) #  . path.consume(len(common_prefix)) node.path.consume(len(common_prefix)) #  Branch- ,  ,    . branches = [b''] * 16 branch_value = value if len(path) == 0 else b'' #     Leaf-  Extension- . self._create_branch_leaf(path, value, branches) self._create_branch_extension(node.path, node.next_ref, branches) branch_reference = self._store_node(Node.Branch(branches, branch_value)) # ,    Extension-. if len(common_prefix) != 0: return self._store_node(Node.Extension(common_prefix, branch_reference)) else: return branch_reference 

الإجراء _create_branch_extension مكافئ منطقياً لإجراء _create_branch_leaf ، لكنه يعمل مع عقدة Extension.

if type(node) == Node.Branch

لكن مع العقدة الفرعية ، كل شيء بسيط. إذا كان المسار فارغًا ، فنحن ببساطة نحفظ القيمة الجديدة في العقدة الفرعية الحالية. إذا لم يكن المسار فارغًا ، فإننا "نعض" قضمًا منه وننزل باستمرار.

الكود ، في اعتقادي ، لا يحتاج إلى تعليقات.

 elif type(node) == Node.Branch: if len(path) == 0: return self._store_node(Node.Branch(node.branches, value)) idx = path.at(0) new_reference = self._update(node.branches[idx], path.consume(1), value) node.branches[idx] = new_reference return self._store_node(node) 

حذف

تفو! تبقى الطريقة الأخيرة. إنه الأكثر مرحًا. تعقيد الحذف هو أننا نحتاج إلى إعادة الهيكل إلى الحالة التي كان من الممكن أن يسقط فيها إذا قمنا بسلسلة update بأكملها ، باستثناء المفتاح المحذوف فقط.

, , , , . "", , .

. , N- , N+1 . enum — DeleteAction , .

delete :

 class MerklePatriciaTrie: # ... # Enum, ,         . class _DeleteAction(Enum): #    . #     , #        (_DeleteAction, None). DELETED = 1, #    (,    ). #     ,    #    : (_DeleteAction, ___). UPDATED = 2, #    Branch-  .   -- #    : # (_DeleteAction, (___, ___)) USELESS_BRANCH = 3 def delete(self, encoded_key): if self._root is None: return path = NibblePath(encoded_key) action, info = self._delete(self._root, path) if action == MerklePatriciaTrie._DeleteAction.DELETED: #   . self._root = None elif action == MerklePatriciaTrie._DeleteAction.UPDATED: #   . new_root = info self._root = new_root elif action == MerklePatriciaTrie._DeleteAction.USELESS_BRANCH: #   . _, new_root = info self._root = new_root def _delete(self, node_ref, path): node = self._get_node(node_ref) if type(node) == Node.Leaf: pass elif type(node) == Node.Extension: pass elif type(node) == Node.Branch: pass 

, get update . . .

if type(node) == Node.Leaf

. . — , , .

:

 if type(node) == Node.Leaf: if path == node.path: return MerklePatriciaTrie._DeleteAction.DELETED, None else: raise KeyError 

, "" — . , . .

if type(node) == Node.Extension

C Extension- :

1. , Extension- . — .
2. _delete , "" .
3. . :

• . .
• . .
• Branch-. . , Branch- . , , Leaf-. — Extension-.

:

 elif type(node) == Node.Extension: if not path.starts_with(node.path): raise KeyError #   . #       . action, info = self._delete(node.next_ref, path.consume(len(node.path))) if action == MerklePatriciaTrie._DeleteAction.DELETED: return action, None elif action == MerklePatriciaTrie._DeleteAction.UPDATED: #    ,     . child_ref = info new_ref = self._store_node(Node.Extension(node.path, child_ref)) return action, new_ref elif action == MerklePatriciaTrie._DeleteAction.USELESS_BRANCH: #     Branch-. stored_path, stored_ref = info # ,     Branch-. child = self._get_node(stored_ref) new_node = None if type(child) == Node.Leaf: #  branch-  . #     Leaf-  Extension. path = NibblePath.combine(node.path, child.path) new_node = Node.Leaf(path, child.data) elif type(child) == Node.Extension: #  Branch-  Extension-. #       . path = NibblePath.combine(node.path, child.path) new_node = Node.Extension(path, child.next_ref) elif type(child) == Node.Branch: #  Branch-      Branch-. #    Extension-    . path = NibblePath.combine(node.path, stored_path) new_node = Node.Extension(path, stored_ref) new_reference = self._store_node(new_node) return MerklePatriciaTrie._DeleteAction.UPDATED, new_reference 

if type(node) == Node.Branch

.

, . Branch-, …

لماذا؟ Branch- Leaf- ( ) Extension- ( ).
, . , — Leaf-. — Extension-. , , 2 — Branch- .

? :

:

1. , .
2. , _delete .

:

 elif type(node) == Node.Branch: action = None idx = None info = None if len(path) == 0 and len(node.data) == 0: raise KeyError elif len(path) == 0 and len(node.data) != 0: node.data = b'' action = MerklePatriciaTrie._DeleteAction.DELETED else: #   ,    . #    . idx = path.at(0) if len(node.branches[idx]) == 0: raise KeyError action, info = self._delete(node.branches[idx], path.consume(1)) #  ,   ,  . #      -    #    . node.branches[idx] = b'' 

_DeleteAction .

1. Branch- , ( , ). .

 if action == MerklePatriciaTrie._DeleteAction.UPDATED: #   . next_ref = info node.branches[idx] = next_ref reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.UPDATED, reference elif action == MerklePatriciaTrie._DeleteAction.USELESS_BRANCH: #    . _, next_ref = info node.branches[idx] = next_ref reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.UPDATED, reference 

1. ( , ), , .

. :

• . , , , . , .
• , . Leaf- . .
• , . , , .
• , , Branch- . , _DeleteAction — UPDATED .

 if action == MerklePatriciaTrie._DeleteAction.DELETED: non_empty_count = sum(map(lambda x: 1 if len(x) > 0 else 0, node.branches)) if non_empty_count == 0 and len(node.data) == 0: # Branch- ,  . return MerklePatriciaTrie._DeleteAction.DELETED, None elif non_empty_count == 0 and len(node.data) != 0: #  ,   . path = NibblePath([]) reference = self._store_node(Node.Leaf(path, node.data)) return MerklePatriciaTrie._DeleteAction.USELESS_BRANCH, (path, reference) elif non_empty_count == 1 and len(node.data) == 0: #  ,   . return self._build_new_node_from_last_branch(node.branches) else: #  1+   ,  2+ . # Branch-  ,   - UPDATED. reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.UPDATED, reference 

_build_new_node_from_last_branch .

— Leaf Extension, , .

— Branch, Extension , , Branch.

 def _build_new_node_from_last_branch(self, branches): #    . idx = 0 for i in range(len(branches)): if len(branches[i]) > 0: idx = i break #     . prefix_nibble = NibblePath([idx], offset=1) #     child = self._get_node(branches[idx]) path = None node = None #   . if type(child) == Node.Leaf: path = NibblePath.combine(prefix_nibble, child.path) node = Node.Leaf(path, child.data) elif type(child) == Node.Extension: path = NibblePath.combine(prefix_nibble, child.path) node = Node.Extension(path, child.next_ref) elif type(child) == Node.Branch: path = prefix_nibble node = Node.Extension(path, branches[idx]) #  . reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.USELESS_BRANCH, (path, reference) 

الباقي

. , … root .

هنا:

 class MerklePatriciaTrie: # ... def root(self): return self._root 

, .

… . , , Ethereum . , , , . , :)

, , pip install -U eth_mpt — .

النتائج

?

, -, , - , , . — , .

-, , , — . , skip list interval tree, — , , .

-, , . , - .

-, — .

, , — !

: 1 , 2 , 3 . ! , .