🤢 🙅🏽 🤠 نحن نمثل خوارزمية الموسيقى لتحديد اتجاه وصول الموجة الكهرومغناطيسية 🌠 👩🏾‍🍳 🔃

aaspcats

مقدمة

سأبدأ مقدمي من بعيد. ذات مرة ، في الفترة البعيدة 2016-2017 ، تمكن خادمك المتواضع من الذهاب في دورة تدريبية مدتها ستة أشهر إلى مدينة إيلمينو البعيدة (ألمانيا) ، حيث أتم بنجاح (إلى حد كبير) برنامج الاتصالات ومعالجة الإشارات لبرنامج الماجستير. لم يكن البرنامج سهلاً ، لكن من الجيد الآن تذكره. في بعض الاحيان ...

لذلك ، في نهاية هذا التدريب ، بالإضافة إلى الدبلوم ، لا يزال لدي عدد قليل من المواد المختلفة في يدي ، والتي اعتقدت أنه من الخطأ عدم مشاركتها.

إحدى هذه المواد أمامك.

ما الأهداف التي اتبعتها أثناء إعداد الندوة :

التحدث عن بعض الأساليب "الذكية" التي تم وضعها بالفعل في موضوع صفائف الهوائي التي يمكن الوصول إليها والقيام بها بالروسية ؛
إجراء محاكاة صغيرة في Python 3 من أجل إثارة زملائه مهندسي الراديو لإلقاء نظرة فاحصة على لغات البرمجة (إذا لم تكن قد نظرت بالفعل عن كثب) ؛
توفير روابط إلى الأدب الجيد باللغة الإنجليزية - دون قراءة المصادر الأجنبية ، الآن ، للأسف ، في أي مكان.

ما يجب مراعاته :

طريقة الموسيقى (تصنيف MUltiple SIgnal) - هذا ، في الواقع ، يشير إلى المعاينة.

يمكن العثور على مثال لتكوين المخطط وطريقة MVDR هنا (إذا كانت هناك أسئلة أو اقتراحات لمواد إضافية ، فيمكن متابعة المناقشة على Github.Gist).

كما قلت أعلاه ، سوف نستخدم بيثون ، وهي:

import numpy as np import matplotlib.pyplot as plt

لماذا لا MATLAB ، واحدة من أكثر المرشحين شعبية ومريحة لنمذجة الجبر الخطي ، تسأل؟ لأنني أريد أن أوضح أنه يمكن القيام بعمل مماثل في بيثون ، وأن نطاق بيثون أوسع بكثير من مجال ماتلاب. لذلك ، فإن التعرف على بناء جملة Python أمر مفيد ، في رأيي.

لنبدأ!

يتم إعداد الصيغ من خلال https://upmath.me/ . شكرا للمبدعين على أداة رائعة!

بيان المشكلة

لنفترض أن هناك مجموعة هوائي خطي تتكون من عدد من العناصر متباعدة بعضها عن بعض $\ Delta = \ frac {\ lambda} {2}$ (خطوة من مجموعة الهوائي) ، حيث $\ امدا$ - طول الموجة الحاملة الكهرمغنطيسية (EM).

تقع الموجات الكهرومغناطيسية على مجموعة الهوائي هذه من اتجاهات مختلفة.

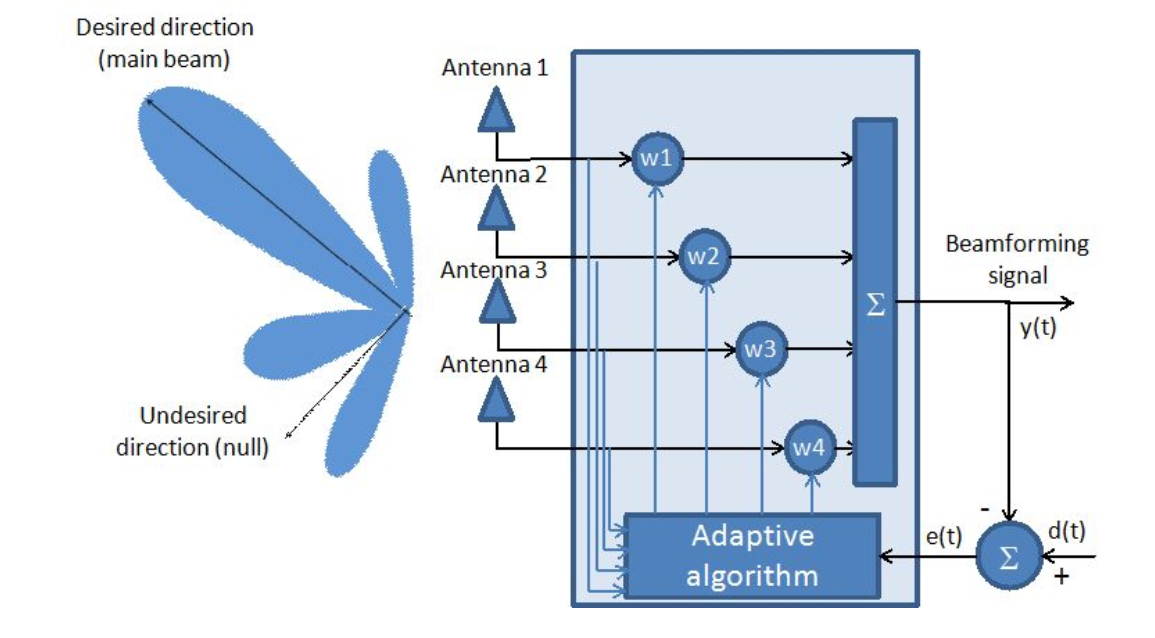
التين. 1. نظام الهوائي التكيفي.

كما يتضح من الشكل ، تُعد مصفوفة الهوائي بمثابة مرشح تكيفي.

في الواقع ، إيجاد المتجه الأمثل للمعاملات ( $\ mathbf {w} _ {opt}$ ) هي المهمة الرئيسية لمصفوفات الهوائي التكيفي من وجهة نظر رياضية.

في البداية ، لا نعرف من أي اتجاهات معينة تأتي الإشارات وعددها. لحل هذا التناقض ، سوف نستخدم خوارزمية MUSIC - خوارزمية لتقدير الترددات المكانية بدقة عالية.

تلقى إشارة المحاكاة

يمكننا تقديم نموذج الإشارة المستقبلة من خلال الصيغة:

$\ mathbf {X} = \ mathbf {A} \ mathbf {S} + \ mathbf {N}$

حيث $\ mathbf {A} = [\ mathbf {a} (\ theta_1) \ quad \ mathbf {a} (\ theta_2) \ quad ... \ quad \ mathbf {a} (\ theta_d)]$ - مصفوفة متجهات المسح (الموجهات التوجيهية) لصفيف الهوائي ( $a_i = \ exp (-j \ mu m_i)$ . $م = 0 ، 1 ... (م -1)$ . $M$ - عدد عناصر صفيف الهوائي ، $د$ - عدد مصادر موجات EM ، $\ ثيتا$ - زاوية اتجاه وصول الموجة EM) ، $\ mathbf {S}$ - مصفوفة الحروف المنقولة ، و $\ mathbf {N}$ - مصفوفة الضوضاء المضافة.

التين. 2. صفيف هوائي خطي متعدد الاتجاهات (ULAA - صفيف هوائي خطي موحد) [1 ، ص. 32].

دعونا نعيد التفكير في هذه الصيغة بطريقة "كل يوم": على شبكتنا نحصل على بعض "الفوضى" من إشارات مختلفة ، والتي نشير إليها $\ mathbf {X}$ . نحن لا نتلقى صراحة معلومات عن عدد المصادر والاتجاهات ، ومع ذلك ، فإن المعلومات المتعلقة بذلك مع ذلك ترد في الإشارة المستلمة.

لقد بدأنا في البحث!

للقيام بذلك ، عادةً ما يشرعوا في التلاعب ليس بمصفوفات اتساع الإشارة المعقدة بأنفسهم ، ولكن مع المتغيرات المشتركة (أي في جوهرها ، مع القوى):

$\ mathbf {R} _ {xx} = \ mathbf {X} \ mathbf {X} ^ H = \ mathbf {A} \ mathbf {R} _ {ss} \ mathbf {A} ^ H + \ mathbf {R} _ {nn}$

الشروط

نقدم شرطًا هامًا للنظر فيه: حد دقة زاوية Rayleigh:

$sin (\ theta_R) = \ frac {\ lambda} {D}$

حيث $D = M \ دلتا$ هو طول شعرية خطية.

نعيد تحديد زاوية وصول الموجة الكهرومغناطيسية من خلال مفهوم التردد المكاني:

$\ mu_R = \ frac {2 \ pi} {\ lambda} \ Delta sin (\ theta_R) = \ frac {2 \ pi} {\ lambda} \ Delta \ frac {\ lambda} {\ Delta M} = \ frac { 2 \ pi} {M}$

حيث $\ mu_R$ - هناك عرض قياسي للفص الرئيسي للحزمة ( عرض الحزمة القياسي ).

للتحقق من مدى فعالية طريقتنا وتحت أي ظروف ، نقدم بعض القيم المعطاة للفصل الزاوي:

$\ mu_1 = - \ mu_R ، \ quad \ mu_2 = 0 ، \ quad \ mu_3 = \ mu_R \ quad$ - التقسيم إلى عرض حزمة واحدة ؛
$\ mu_1 = -0.5 \ mu_R ، \ quad \ mu_2 = 0 ، \ quad \ mu_3 = 0.5 \ mu_R \ quad$ - التقسيم إلى عرض حزمة واحدة ثانية ؛
$\ mu_1 = -0.3 \ mu_R ، \ quad \ mu_2 = 0 ، \ quad \ mu_3 = 0.3 \ mu_R \ quad$ - تقسيم إلى ثلاثة أعشار عرض الشعاع.

تحديد معلمات الإدخال:

 M = 10 #    () SNR = 10 #  - (dB) d = 3 #     N = 50 #  "" (snapshots) S = ( np.sign(np.random.randn(d,N)) + 1j * np.sign(np.random.randn(d,N)) ) / np.sqrt(2) # QPSK W = ( np.random.randn(M,N) + 1j * np.random.randn(M,N) ) / np.sqrt(2) * 10**(-SNR/20) # AWGN #  : # sqrt(N0/2)*(G1 + jG2), #  G1  G2 -   . # .. Es( )  QPSK  1 ,    (noise spectral density): # N0 = (Es/N)^(-1) = SNR^(-1) [] (   ,  SNR = Es/N0); #    : # SNR_dB = 10log10(SNR) => N0_dB = -10log10(SNR) = -SNR_dB []; #    SNR    (..  ),   : # SNR = 10^(SNR_dB/10) => sqrt(N0) = (10^(-SNR_dB/10))^(1/2) = 10^(-SNR_dB/20) mu_R = 2*np.pi / M

وهناك القليل من النظرية حول الطريقة نفسها

بادئ ذي بدء ، نلاحظ أن السلف لطريقة MUSIC هو طريقة Pisarenko (1973). كانت المشكلة المدروسة في طريقة بيسارينكو هي تقدير ترددات مجموع الأسس المعقدة في الضوضاء البيضاء. أثبت V.F. Pisarenko أنه يمكن العثور على الترددات من متجهات eigenvectors المقابلة للحد الأدنى من القيمة الذاتية لمصفوفة الارتباط التلقائي. بعد ذلك ، أصبحت هذه الطريقة حالة خاصة لطريقة الموسيقى. [2 ، ص. 459]

اقترح شميدت وزملاؤه خوارزمية تصنيف الإشارات المتعددة (MUSIC) في عام 1979 [4]. يتمثل النهج الرئيسي لهذه الخوارزمية في تحليل مصفوفة التغاير للإشارة المستقبلة إلى القيم الذاتية. نظرًا لأن هذه الخوارزمية تأخذ في الاعتبار الضوضاء غير المرتبطة ، فإن مصفوفة التغاير الناتجة لها شكل قطري. هنا ، يتم حساب المساحات الفرعية للإشارة والضوضاء باستخدام الجبر الخطي ، وتكون متعامدة مع بعضها البعض. لذلك ، تستخدم الخوارزمية خاصية التعامد لاستخراج المساحات الفرعية للإشارة والضوضاء [5].

يمكن تعريف خوارزمية MUSIC المعممة على النحو التالي:

العثور على مصفوفة التغاير $\ mathbf {R} _ {xx}$
البحث عن متجهات eigenvectors عبر EVD أو خوارزمية رقمية مناسبة أخرى:

$\ mathbf {R} _ {xx} = \ mathbf {U} \ mathbf {\ Lambda} \ mathbf {U} ^ H \ qquad (1)$

ابحث عن الطيف الزائف (لماذا باستخدام البادئة الزائفة ، سنناقش أدناه) MUSIC من خلال الصيغة التالية:

$P_ {MU} (e ^ {j \ omega}) = \ frac {1} {\ sum \ limit_ {i = d + 1} ^ {M} | \ mathbf {a} ^ H \ mathbf {u} _i | ^ 2} \ qquad (2)$

حيث $\ mathbf {a} = \ start {bmatrix} e ^ {j0 \ omega} & e ^ {j1 \ omega} & e ^ {j2 \ omega} & ... & e ^ {j (M-1) \ omega } \ end {bmatrix} ^ T$ هو متجه الأسس للتردد ω الكذب في مدى معين ، و $\ mathbf {u} _i$ - عامل التهيئة e-th (متجه eigen) لمصفوفة التغاير (1) المطابق للفضاء الفرعي للضوضاء للمصفوفة (1) - ومن ثم فإن الفهرسة مع $د + 1$ ( $د$ هي رتبة المصفوفة (1)).

لمزيد من الوضوح ، حاول تشغيل البرنامج النصي MATLAB المناسب الذي يتم توفيره حسب المرجع . انتبه لنقطتين رئيسيتين:
بدلاً من حساب مربع القاعدة الثانية في المقام (2) ، يطبق المؤلفون خوارزمية FFT على المتجهات الذاتية ، التي تسهل النمذجة باستخدام الدوال المضمنة ، وبشكل عام ، لا تتعارض مع النظرية من وجهة نظر رياضية ؛
يتم حساب مصفوفة التغاير من خلال المصفوفات التلافيفية ؛ وقد تم عرض نهج مختلف أعلاه لتقدير الترددات المكانية.

كما قد تخمين من الاسم ، MUSIC هي أيضًا طريقة كلاسيكية لتقدير اتجاه الاستقبال بدقة عالية. فيما يلي خوارزمية حساب الأطياف الزائفة في هذا السياق:

نجد مصفوفة التغاير للإشارة المستقبلة ؛
العثور على صفر مساحة فرعية $\ mathbf {U} _0$ :

$\ mathbf {U} = [\ mathbf {U} _s \ quad \ mathbf {U} _0]$

حدد بعض نطاق البحث:

$a (\ mu) = \ start {bmatrix} e ^ {j0 \ mu_1} & ... & e ^ {j0 \ mu_Q} \\ ... & ... & ... \\ e ^ {j ( M-1) \ mu_1} & ... & e ^ {j (M-1) \ mu_Q} \ end {bmatrix}$

حيث $\ mu = - \ frac {2 \ pi f_c} {c} \ Delta sin \ theta = - \ frac {2 \ pi} {\ lambda} \ Delta sin \ theta$

احسب الطيف الزائف:

$P_ {MU} (\ theta) = \ frac {\ mathbf {a} ^ H (\ theta) \ mathbf {a} (\ theta)} {\ mathbf {a} ^ H (\ theta) \ mathbf {U} _0 \ mathbf {U} _0 ^ H \ mathbf {a} (\ theta)}$

تم وصف العلاقة بين التحليل الطيفي وتحليل زوايا الوصول (DoA - اتجاه arriaval) لموجات EM في الجدول 1.

الجدول 1 التواصل بين تطبيقات الموسيقى : معالجة مجموعة الإشارة والبحث التوافقي [6].

متغير	معالجة مجموعة الإشارة	البحث التوافقي
$M$	عدد من أجهزة الاستشعار	عدد الفترات الزمنية
$N$	عدد الفترات الزمنية	عدد التجارب
$د$	عدد جبهات الموجة	عدد المكونات المعقدة
$\ mu$	الترددات المكانية	ترددات طبيعية

بشكل عام ، يمكن مقارنة عملية الاستلام من خلال المصفوفات (حواجز شبكية) مع عملية التقديرية الكلاسيكية ، لأن في الواقع ، كل مستشعر ، يستقبل موجة مع تأخير طور معين (أي مع تأخير زمني معين) ، يؤدي وظائف نبض دلتا أخذ العينات. سيتوافق عدد عمليات الإنجاز (التجارب) للتحليل الطيفي الكلاسيكي مع عدد مقاطع الوقت (لقطات). سيكون لكل مصدر واجهة الموجة الخاصة به ، وهو ما يعادل عدد الجيوب الأنفية الفريدة للإشارة في حالة التحليل الطيفي.

والآن عدنا إلى لحظة حساب المتغيرات الذاتية. ذكرنا بالفعل أعلاه أن ناقلات $a (\ theta_i) \ epsilon A$ حيث $أنا = 1،2 ، .. ، د$ متعامد مع فضاء الضوضاء في مصفوفة التغاير ، أي:

$a (\ theta_i) ^ TU_0 = 0 ^ T$

في الواقع ، نرى نظام المعادلات ، حل يمكن أن نجد الجذور - eigenvectors. مثل هذه الطريقة ، على عكس الخوارزميات العددية (التي ، كما ذكرنا أعلاه ، تنطبق على EVD) ، تسمح لأحدها بالحصول على قيم متماثلة حقيقية وليست تقريبية. هذا هو السبب في أن هذا النهج يسمح لنا بالحصول على ليس كاذب ، ولكن الطيف. شكلت نفس الفكرة أساس خوارزمية الجذر MUSIC .

تصميم

Fuf! أخيرًا ، يتم وصف جميع الصيغ وشرحها إلى حد ما. يمكننا أن نبدأ النمذجة.

 cases = [[-1., 0, 1.], [-0.5, 0, 0.5], [-0.3, 0, 0.3],] for idxm, c in enumerate(cases): #   ( ): mu_1 = c[0]*mu_R mu_2 = c[1]*mu_R mu_3 = c[2]*mu_R #   a_1 = np.exp(1j*mu_1*np.arange(M)) a_2 = np.exp(1j*mu_2*np.arange(M)) a_3 = np.exp(1j*mu_3*np.arange(M)) A = (np.array([a_1, a_2, a_3])).T #    X = np.dot(A,S) + W #    R = np.dot(X,np.matrix(X).H) U, Sigma, Vh = np.linalg.svd(X, full_matrices=True) U_0 = U[:,d:] #   thetas = np.arange(-90,91)*(np.pi/180) #   mus = np.pi*np.sin(thetas) #    a = np.empty((M, len(thetas)), dtype = complex) for idx, mu in enumerate(mus): a[:,idx] = np.exp(1j*mu*np.arange(M)) # MVDR: S_MVDR = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MVDR[idx] = 1 / (np.dot(np.matrix(a_idx).H, np.dot(np.linalg.pinv(R),a_idx))) # MUSIC: S_MUSIC = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MUSIC[idx] = np.dot(np.matrix(a_idx).H,a_idx)\ / (np.dot(np.matrix(a_idx).H, np.dot(U_0,np.dot(np.matrix(U_0).H,a_idx)))) plt.subplots(figsize=(10, 5), dpi=150) plt.semilogy(thetas*(180/np.pi), np.real( (S_MVDR / max(S_MVDR))), color='green', label='MVDR') plt.semilogy(thetas*(180/np.pi), np.real((S_MUSIC/ max(S_MUSIC))), color='red', label='MUSIC') plt.grid(color='r', linestyle='-', linewidth=0.2) plt.xlabel('Azimuth angles θ (degrees)') plt.ylabel('Power (pseudo)spectrum (normalized)') plt.legend() plt.title('Case #'+str(idxm+1)) plt.show()

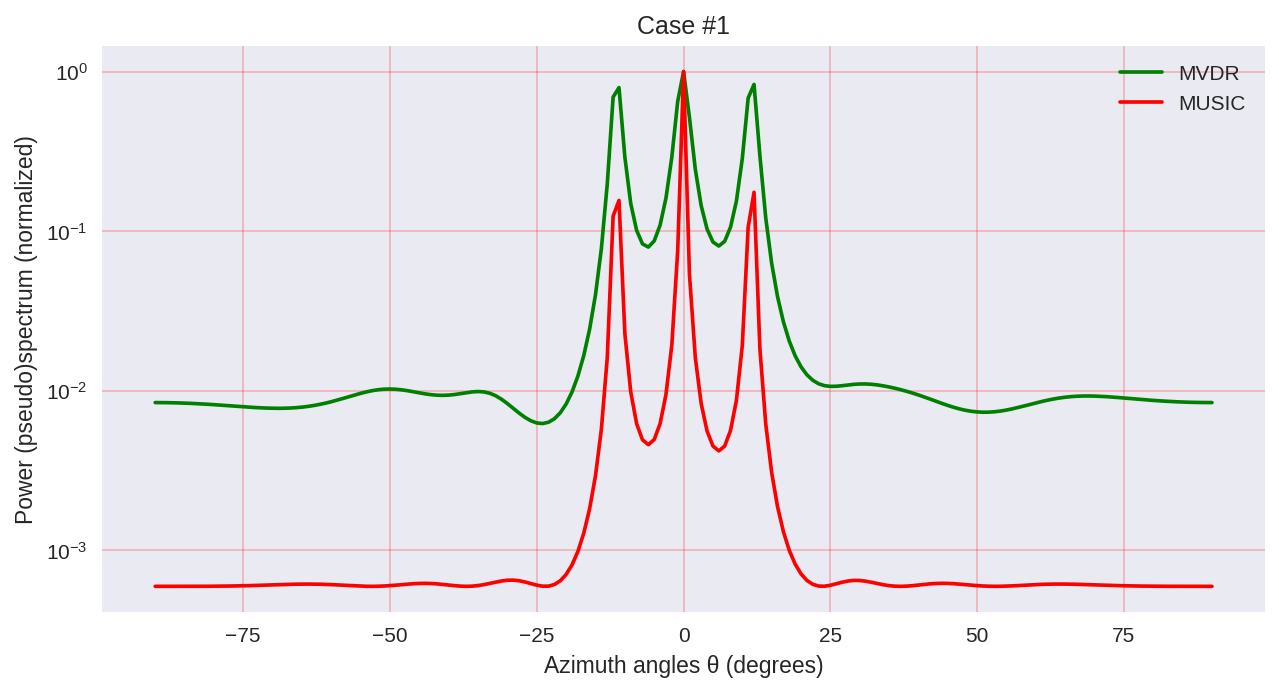
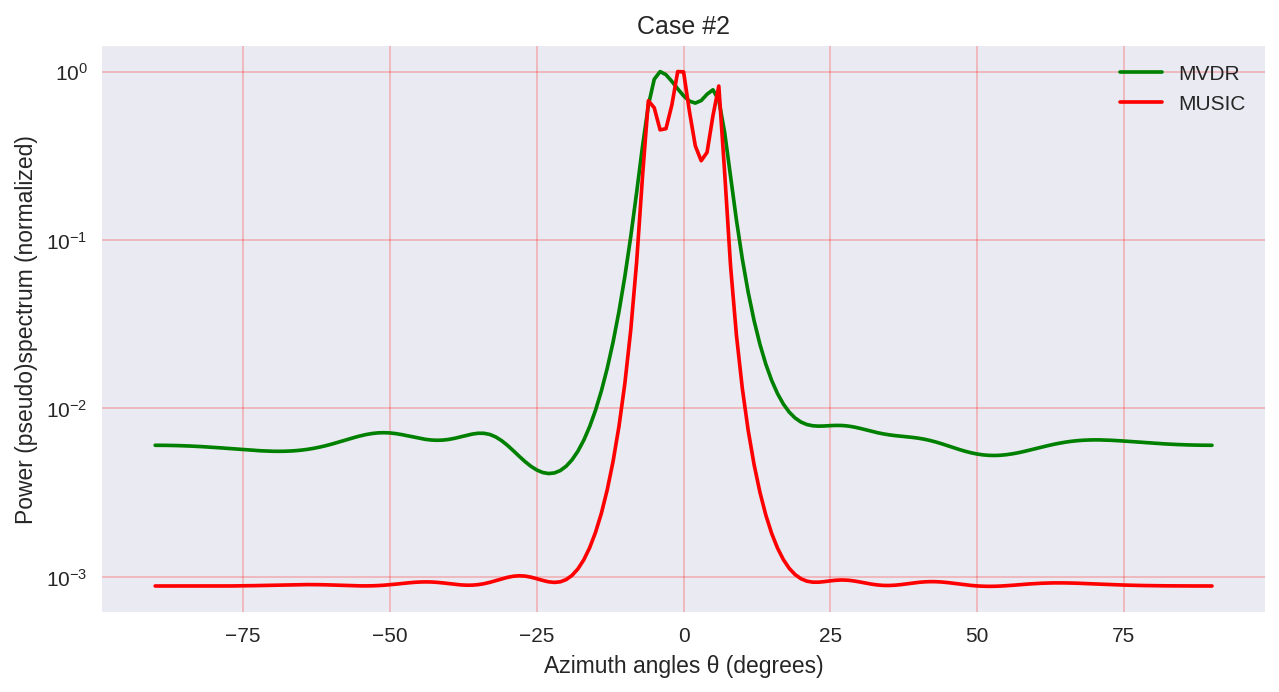
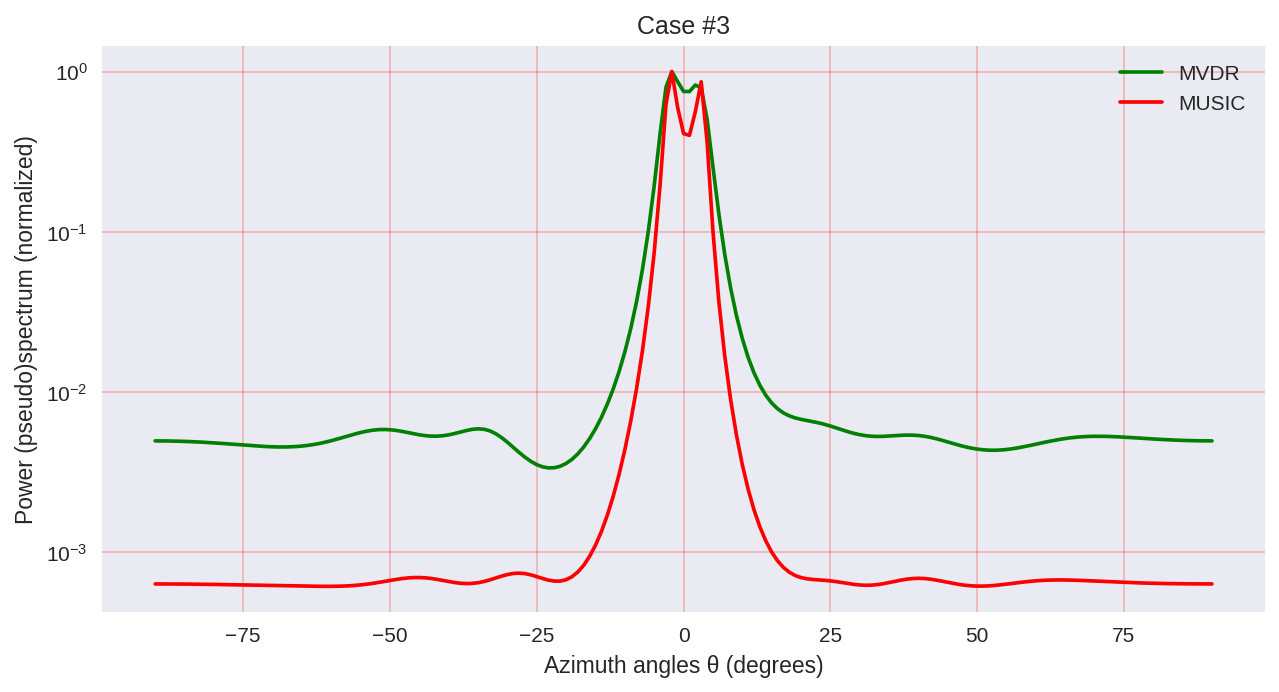
كما نرى ، تتمتع MUSIC بدقة أعلى وتسمح بتحقيق نتائج أفضل بشكل عام ، على سبيل المثال ، تسمح MVDR - نفس ممثل الطرق التحليلية الطيفية.

ومع ذلك ، يجب ألا يغيب عن البال أنه عند استخدام MUSIC ، نستخدم خوارزميات أكثر تكلفة حسابيًا ، مثل EVD أو SVD ، والتي هي في بعض الأسعار للحصول على دقة أكبر.

مثل هذه الأشياء.

قائمة الأدبيات المستخدمة:

هايكين ، سيمون ، وكي جي راي ليو. كتيب عن معالجة مجموعة وشبكات الاستشعار. المجلد. 63. جون وايلي وأولاده ، 2010. ص. 102-107
Hayes MH الإحصائية معالجة الإشارات الرقمية والنمذجة. - جون وايلي وأولاده ، 2009.
Haykin، Simon S. Adaptive filter theory. Pearson Education India، 2008. pp. 422-427
ريتشموند ، كريستيان د. "كابون خوارزمية خطأ متوسط التربيع عتبة التنبؤ SNR واحتمال الحل." معاملات IEEE على معالجة الإشارات 53.8 (2005): 2748-2764.
SKP Gupta ، MUSIC وخوارزمية MUSIC محسّنة لإثارة dorection وصول ، IEEE ، 2015.
محاضرات البروفيسور مارتن هارت ( صفيف )

نحن نمثل خوارزمية الموسيقى لتحديد اتجاه وصول الموجة الكهرومغناطيسية