التعلم العميق في حساب التدفق البصري

مع ظهور العديد من تصميمات الشبكات العصبية المختلفة ، فإن العديد من تقنيات رؤية الكمبيوتر الكلاسيكية هي شيء من الماضي. في كثير من الأحيان ، يستخدم الناس SIFT و HOG للكشف عن الأشياء ، و MBH للتعرف على الإجراءات ، وإذا كانوا يستخدمونها ، فسيكون ذلك أشبه بالإشارات اليدوية للشبكات المقابلة. سننظر اليوم في واحدة من مشاكل السيرة الذاتية الكلاسيكية التي ما زالت الأساليب التقليدية تتصدرها ، في حين تتنفسها أبنية DL في الجزء الخلفي من الرأس.

تقدير التدفق البصري

تتمثل مهمة حساب التدفق البصري بين صورتين (عادة بين الإطارات المجاورة للفيديو) في إنشاء حقل متجه $$$يا دولا$بنفس الحجم ، علاوة على ذلك $$$O (i، j)$سوف تتوافق مع متجه النزوح بكسل واضحة $$$(i، j)$من الإطار الأول إلى الثاني. من خلال إنشاء حقل متجه من هذا القبيل بين جميع الإطارات المجاورة للفيديو ، نحصل على صورة كاملة عن كيفية تحرك كائنات معينة عليه. بمعنى آخر ، هذه هي مهمة تتبع جميع وحدات البكسل في الفيديو. يتم استخدام الدفق البصري على نطاق واسع للغاية - في مهام التعرف على الإجراءات ، على سبيل المثال ، يسمح لك حقل المتجه هذا بالتركيز على الحركات التي تحدث على الفيديو والابتعاد عن سياقه [7]. التطبيقات الأكثر شيوعًا هي القياس البصري وضغط الفيديو والمعالجة اللاحقة (على سبيل المثال ، إضافة تأثير بطيء الحركة) وأكثر من ذلك بكثير.



هناك متسع لبعض الغموض - ما هو بالضبط التحيز المرئي من وجهة نظر الرياضيات؟ عادةً ما يُفترض أن قيم البيكسل تنتقل من إطار إلى آخر بدون تغييرات ، بمعنى آخر:

$$

$$I (i، j، t) = I (i + u_i، j + u_j، t + 1)،$$

حيث $$$I (i، j، t)$- كثافة بكسل في الإحداثيات $$$(i، j)$ثم التدفق البصري $$$(u_i، u_j)$يوضح مكان انتقال البيكسل إلى النقطة التالية في الوقت المناسب (على سبيل المثال ، في الإطار التالي).

في الصورة يبدو مثل هذا:





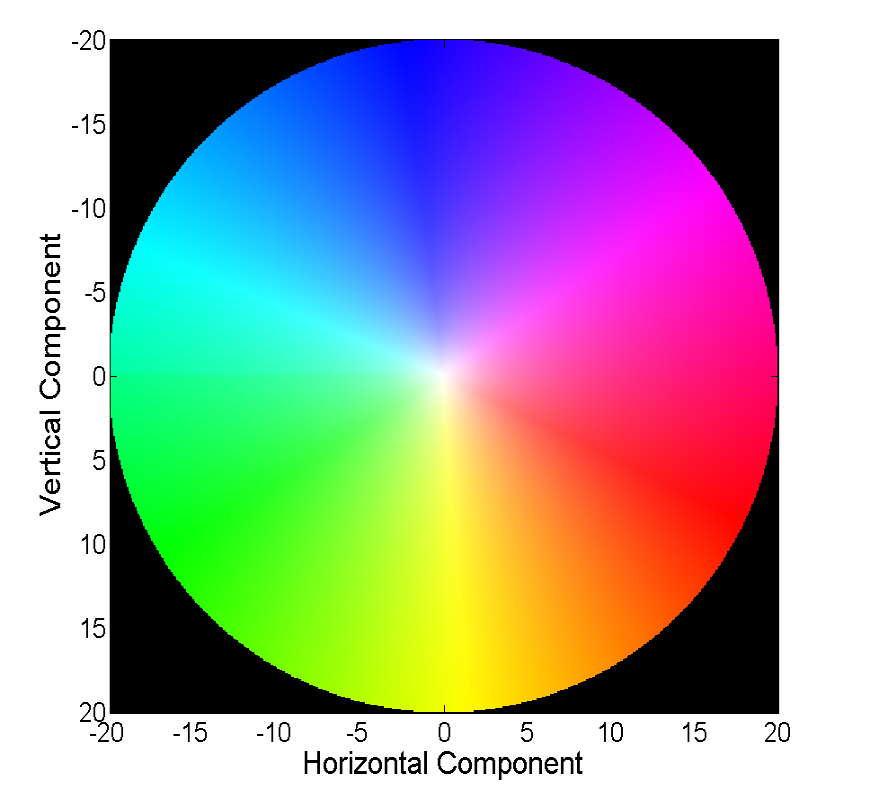
إن التصور المرئي لحقل متجه مباشرة باستخدام المتجهات مرئي ، ولكنه ليس مناسبًا دائمًا ، وبالتالي فإن الطريقة الشائعة الثانية هي التصور مع اللون:





كل لون في هذه الصورة يشفر متجه معين. للبساطة ، يتم اقتصاص المتجهات التي يزيد طولها عن 20 ، ويمكن استعادة المتجه نفسه بلون من الصورة التالية:




لقد حققت الأساليب الكلاسيكية دقة جيدة جدًا ، والتي تأتي في بعض الأحيان بسعر. سننظر في التقدم الذي حققته الشبكات العصبية في حل هذه المشكلة خلال السنوات الأربع الماضية.

البيانات والمقاييس

كلمتين حول مجموعات البيانات التي كانت متاحة وشائعة في بداية قصتنا (أي 2015) ، وكذلك كيفية قياس جودة الخوارزمية الناتجة.

ميدلبري

مجموعة بيانات صغيرة من 8 أزواج من الصور مع إزاحات صغيرة ، والتي ، مع ذلك ، تستخدم أحيانًا في التحقق من الخوارزميات لحساب التدفق البصري حتى الآن.

كيتى

هذه مجموعة بيانات تم ترميزها لتطبيقات السيارات ذاتية القيادة وتجميعها باستخدام تقنية LIDAR. يستخدم على نطاق واسع للتحقق من صحة خوارزميات حساب التدفق البصري ويحتوي على العديد من الحالات المعقدة إلى حد ما مع التحولات الحادة بين الإطارات.

Sintel

معيار آخر شائع للغاية ، تم إنشاؤه على أساس الفتح والرسم في كارتون Blender Sintel في نسختين ، والتي تم تصنيفها على أنها نظيفة ونهائية. والثاني هو أكثر تعقيدا بكثير ، لأنه يحتوي على الكثير من التأثيرات الجوية ، والضوضاء ، وطمس وغيرها من المشاكل لخوارزميات لحساب التدفق البصري.

EPE

وظيفة الخطأ القياسية لمهمة حساب التدفق البصري هي End Point Error أو EPE. هذه هي ببساطة المسافة الإقليدية بين الخوارزمية المحسوبة والتدفق البصري الحقيقي ، حيث يتم حساب المتوسط ​​على جميع وحدات البكسل.

فلونت (2015)

عند الشروع في إنشاء بنية شبكة عصبية لمهمة حساب التدفق البصري مرة أخرى في عام 2015 ، واجه المؤلفون (من جامعتي ميونيخ وفرايبورج) مشكلتين: لم تكن هناك مجموعة بيانات كبيرة ملحوظة لهذه المهمة ، ووضع علامة عليها يدويًا سيكون صعبًا (حاول تحديد المكان الذي انتقلت إليه) كل بكسل من الصورة على الإطار التالي) ، أولا. كانت هذه المهمة مختلفة تمامًا عن جميع المهام التي تم حلها بمساعدة CNN-architectures قبل ذلك ، ثانياً. في الواقع ، هذه مهمة انحدار بكسل لكل بكسل ، مما يجعلها تشبه مهمة التقسيم (تصنيف بكسل لكل بكسل) ، ولكن بدلاً من صورة واحدة ، لدينا مدخلتان ، وبشكل حدسي ، يجب أن تُظهر الإشارات الفرق بين الصورتين. كالتكرار الأول ، تقرر ببساطة نشر إطارين RGB كمدخلات (تلقينا في الواقع صورة ذات 6 قنوات) ، والتي نريد حساب الدفق البصري بينها ، ونأخذ U-net كعمارة مع عدد من التغييرات. هذه الشبكة كانت تسمى FlowNetS (S لتقف على البساطة):





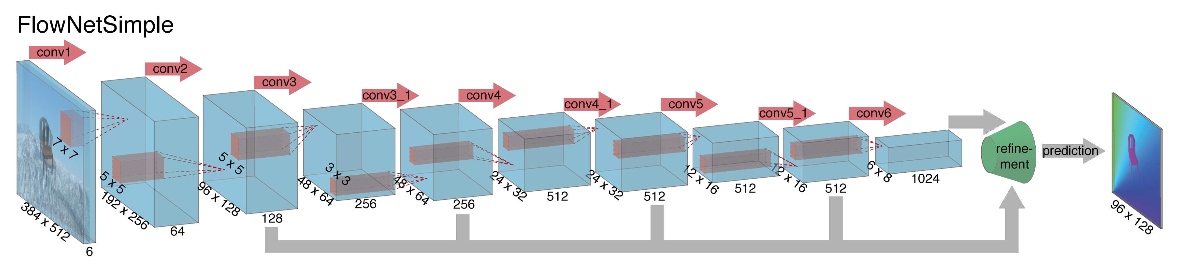
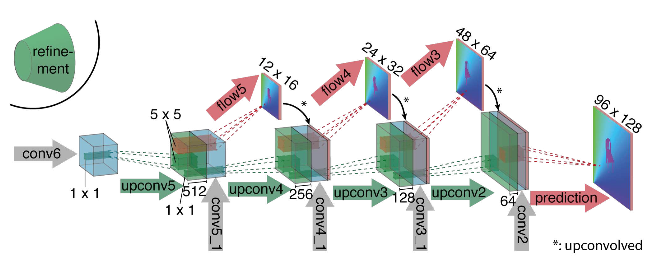
كما ترون من الرسم التخطيطي ، جهاز التشفير غير ملحوظ ، فك التشفير يختلف عن الخيارات الكلاسيكية بعدة طرق:

1. يحدث التنبؤ بالتدفق البصري ليس فقط من المستوى الأخير ، ولكن أيضًا من جميع المستويات الأخرى. للحصول على "الحقيقة الأساسية" لمستوى i-th من وحدة فك الترميز ، يتم ببساطة خفض الهدف الأصلي (أي الدفق البصري) (تقريبًا نفس الصورة) إلى الدقة المطلوبة ، ويزيد المسند الناتج عن المستوى i ، على سبيل المثال ، يتم ربطها بخريطة معالم ناشئة من هذا المستوى. ستكون الوظيفة العامة لفقدان التدريب عبارة عن مجموع مرجح للخسائر من جميع مستويات وحدة فك الترميز ، بينما سيكون الوزن نفسه أكبر ، كلما كان المستوى أقرب إلى إخراج الشبكة. لا يقدم المؤلفون شرحًا لسبب القيام بذلك ، ولكن على الأرجح السبب هو أن الحركات الحادة من الأفضل اكتشافها في المستويات المبكرة ، فلن تكون المتجهات كبيرة جدًا على الدفق البصري ذي الدقة المنخفضة.
2. يوضح الرسم البياني أن دقة إدخال الصور هي 384 × 512 ، والإخراج أصغر أربع مرات. لاحظ المؤلفون أنه إذا قمت بزيادة هذا الإخراج إلى 384 × 512 عن طريق الاستيفاء البسيط ذو الخطين ، فسوف يعطي نفس الجودة كما لو قمت بإرفاق مستويين آخرين من وحدة فك الترميز. يمكنك أيضًا استخدام النهج التبايني [2] ، والذي يثبت الجودة (+ v في الجدول بالجودة).
3. كما هو الحال في U-net ، يتم إرسال بطاقات السمات من المشفر إلى وحدة فك الترميز ومتسلسلة كما هو موضح في الرسم التخطيطي.

لفهم كيف حاول المؤلفون تحسين خطهم الأساسي ، تحتاج إلى معرفة العلاقة بين الصور ولماذا يمكن أن تكون مفيدة في حساب التدفق البصري. لذلك ، بعد الحصول على صورتين ومعرفة أن الثانية هي الإطار التالي في الفيديو نسبة إلى الأولى ، يمكننا محاولة مقارنة المنطقة المحيطة بنقطة على الإطار الأول (والتي نريد أن نوجد تحولًا إلى الإطار الثاني) بها مساحات من نفس الحجم في الصورة الثانية. علاوة على ذلك ، بافتراض أن التحول لا يمكن أن يكون كبيرًا جدًا لكل وحدة زمنية ، يمكن اعتبار المقارنة فقط في حي معين من نقطة البداية. لهذا ، يتم استخدام الارتباط المتبادل. دعونا توضيح مع مثال.

خذ إطارين متجاورين للفيديو ، نريد تحديد المكان الذي تحولت فيه نقطة معينة من الإطار الأول إلى الثاني. لنفترض أن بعض المناطق المحيطة بهذه النقطة قد تحولت بنفس الطريقة. في الواقع ، عادة ما يتم تعويض وحدات البكسل المجاورة في الفيديو معًا على الأرجح ، بصريا ، هي جزء من كائن واحد. يستخدم هذا الافتراض بنشاط ، على سبيل المثال ، في الطرق التفاضلية ، والتي يمكن قراءتها بمزيد من التفصيل في [5] ، [6].

fig, ax = plt.subplots(1, 2, figsize=(20, 10)) ax[0].imshow(frame1) ax[1].imshow(frame2); 

دعونا نحاول أن نأخذ نقطة في وسط مخلب القط الصغير ونجده في الإطار الثاني. خذ بعض المنطقة من حوله.

 patch1 = frame1[90:190, 140:250] plt.imshow(patch1); 

نحسب العلاقة بين هذه المنطقة (في الأدب الإنجليزي ، غالبًا ما نكتب قالبًا أو تصحيحًا من الصورة الأولى) والصورة الثانية. سيقوم القالب ببساطة "بالتجول" عبر الصورة الثانية وحساب القيمة التالية بينها وبين القطع من نفس الحجم في الصورة الثانية:



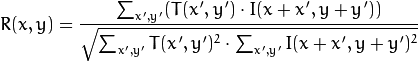
كلما زادت قيمة هذه القيمة ، كلما بدا القالب مثل القطعة المقابلة في الصورة الثانية. مع OpenCV ، يمكن القيام بذلك مثل هذا:

 corr = cv2.matchTemplate(frame2, patch1, cv2.TM_CCORR_NORMED) plt.imshow(corr, cmap='gray'); 

يمكن الاطلاع على مزيد من التفاصيل في [7].

والنتيجة هي كما يلي:



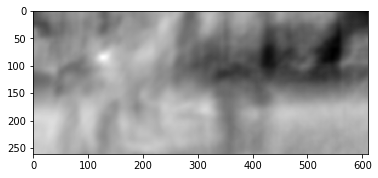
نرى ذروة واضحة ، المشار إليها باللون الأبيض. العثور عليه في الإطار الثاني:

 min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(corr) h, w, _ = patch1.shape top_left = max_loc bottom_right = (top_left[0] + w, top_left[1] + h) frame2_copy = frame2.copy() cv2.rectangle(frame2_copy, top_left, bottom_right, 255, 2) plt.imshow(frame2_copy); 

نرى أنه تم العثور على القدم بشكل صحيح ، ووفقًا لهذه البيانات ، يمكننا أن نفهم في أي اتجاه انتقل من الإطار الأول إلى الثاني وحساب التدفق البصري المقابل. بالإضافة إلى ذلك ، اتضح أن هذه العملية مقاومة تمامًا للتشوهات الضوئية ، أي إذا ارتفع السطوع في الإطار الثاني بحدة ، فستظل ذروة الارتباط المتبادل بين الصور في مكانها.

وبالنظر إلى كل ما سبق ، قرر المؤلفون إدخال ما يسمى طبقة الارتباط في بنيتهم ​​، ولكن تقرر عدم النظر في الارتباط وفقًا لصور المدخلات ، ولكن وفقًا لخرائط السمات بعد عدة طبقات من المشفر. مثل هذه الطبقة ، لأسباب واضحة ، لا تحتوي على معلمات تعليمية ، على الرغم من أنها تشبه في جوهرها الإلتواء ، ولكن بدلاً من المرشحات ، نستخدم هنا ليس الأوزان ، ولكن بعض المناطق في الصورة الثانية:



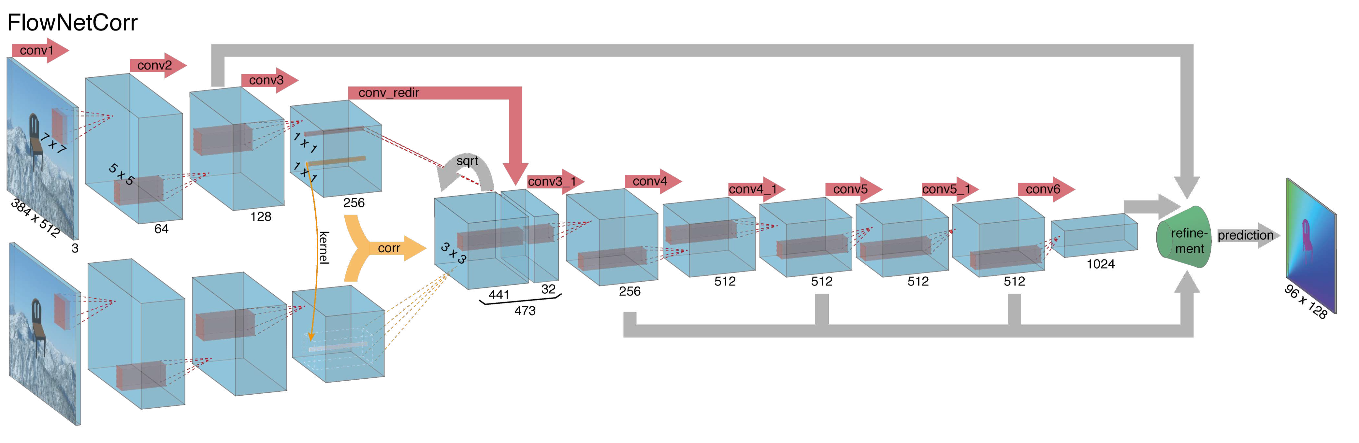
ومن الغريب أن هذه الحيلة لم تقدم تحسينًا كبيرًا في جودة مؤلفي هذه المقالة ، ومع ذلك ، فقد تم تطبيقها بنجاح أكبر في أعمال أخرى ، وفي [9] تمكن المؤلفون من إظهار أنه من خلال تغيير معلمات التدريب قليلاً ، يمكن جعل FlowNetC يعمل بشكل أفضل.

قام المؤلفون بحل المشكلة مع عدم وجود مجموعة بيانات بطريقة أنيقة إلى حد ما: قاموا بإزالة 964 صورة من فليكر حول الموضوعات: "المدينة" ، "المناظر الطبيعية" ، "الجبل" بدقة 1024 × 768 واستخدموا محاصيلهم 512 × 384 كخلفية ، والتي رموا بعدد قليل منها كراسي من مجموعة مفتوحة من النماذج ثلاثية الأبعاد المقدمة. بعد ذلك ، تم تطبيق تحويلات مختلفة على تقارب مستقل على الكراسي والخلفية ، والتي استخدمت لإنشاء الصورة الثانية في زوج وتدفق بصري بينهما. والنتيجة هي كما يلي:





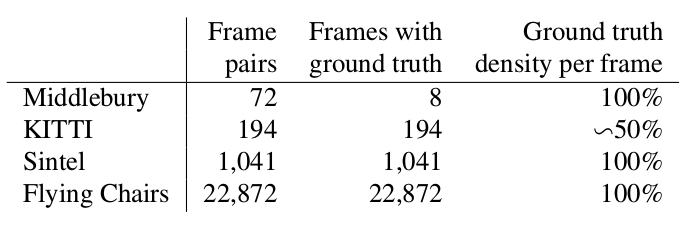
وكانت إحدى النتائج المثيرة للاهتمام هي أن استخدام مجموعة البيانات الاصطناعية هذه مكّن من تحقيق جودة جيدة نسبيًا للبيانات من مجال آخر. أثبت التنقيح الدقيق للبيانات المقابلة ، بطبيعة الحال ، مزيدًا من الصفات (+ قدم في الجدول أدناه):



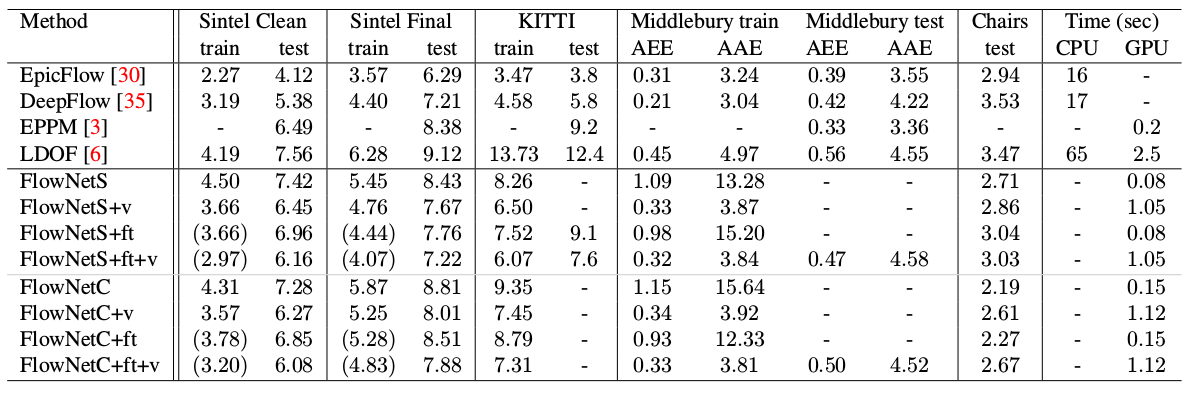
يمكن مشاهدة النتيجة على مقاطع الفيديو الحقيقية هنا:

SpyNet (2016)

في العديد من المقالات اللاحقة ، حاول المؤلفون تحسين الجودة من خلال حل مشكلة ضعف الاعتراف بالحركات المفاجئة. بشكل حدسي ، لن يتم التقاط الحركة من قبل الشبكة إذا كان متجهها يتجاوز بشكل ملحوظ مجال التنشيط التقديري. يُقترح حل هذه المشكلة بسبب ثلاثة أشياء: الإلتواء الأكبر والأهرام و "تزييف" صورة واحدة من زوج إلى دفق بصري. كل شيء بالترتيب.

لذلك ، إذا كان لدينا عدة صور تحول الكائن فيها بحدة (10+ بكسل) ، فيمكننا ببساطة تقليل الصورة (بمقدار 6 مرات أو أكثر). ستنخفض القيمة المطلقة للإزاحة بشكل كبير ، ومن المرجح أن تكون الشبكة قادرة على "التقاطها" ، خاصةً إذا كانت ملفاتها أكبر من الإزاحة نفسها (في هذه الحالة ، يتم استخدام ملفات 7x7).



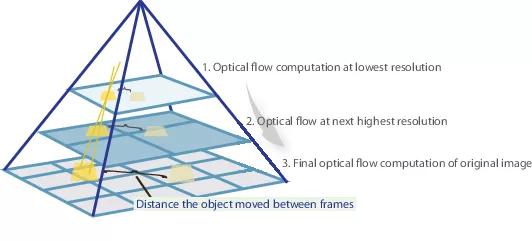
ومع ذلك ، عند تصغير الصورة ، فقدنا الكثير من التفاصيل المهمة ، لذلك يجب أن ننتقل إلى المستوى التالي من الهرم ، حيث يكون حجم الصورة أكبر بالفعل ، مع الأخذ في الاعتبار المعلومات التي تلقيناها من قبل عندما نحسب التدفق الضوئي بحجم أصغر. يتم ذلك باستخدام عامل التزييف ، الذي يحسب الصورة الأولى وفقًا للتقريب المتاح للتدفق البصري (تم الحصول عليه في المستوى السابق). أحد التحسينات في هذه الحالة هو أن الصورة الأولى التي يتم "دفعها" وفقًا لتقريب التدفق البصري ستكون أقرب إلى الثانية مقارنة بالصورة الأصلية ، أي أننا نقلل مرة أخرى القيمة المطلقة للتدفق البصري ، والتي نحتاج إلى التنبؤ بها (تذكر ، قيمة صغيرة تم الكشف عن الحركات بشكل أفضل ، حيث يتم تضمينها بالكامل في ملف واحد). من وجهة نظر الرياضيات ، وجود صورة نقطية I وتقريب التدفق البصري V ، يمكن وصف عامل الالتواء على النحو التالي:

$$

$$w (I، V) = I_w، \؛ \؛ I_w (x) = I (x + V (x)) ،$$

حيث $$$x = (i، j)$، أي نقطة محددة في الصورة $$$I$- الصورة نفسها $$$V$- التدفق البصري $$$I_w$- الصورة الناتجة ، "ملفوفة" في الدفق البصري.

كيفية تطبيق كل هذا في بنية CNN؟ نصلح عدد مستويات الهرم $$$ك$والعامل الذي يتم به تقليل كل صورة تالية عند مستوى يبدأ من آخر $$$ن$. دلالة بواسطة $$$d (*)$و $$$u (*)$وظائف الاختزال والتقاطع للصورة أو التدفق البصري بواسطة هذا العامل.

سنحصل أيضًا على مجموعة من CNN-ok { $$$G_0 ... G_k$} واحد لكل مستوى من الهرم. ثم $$$G_i$شبكة عشر سوف تقبل زوجين من الصور مع $$$i$مستوى الهرم والتدفق البصري يحسب على $$$G_ {i-1}$المستوى ( $$$G_0 دولا$لن يقبل سوى موتر الأصفار بدلاً من ذلك). في هذه الحالة ، سوف نرسل إحدى الصور إلى طبقة الالتواء لتقليل الفارق بينها ، ولن نتنبأ بالتدفق البصري في هذا المستوى ، ولكن القيمة التي يجب إضافتها إلى التدفق البصري المتزايد (المضاعف) من المستوى السابق للحصول على التدفق البصري في هذا المستوى. في الصيغة ، يبدو مثل هذا:

$$

$$v_k = G_k (I_k ^ 1 ، w (I_k ^ 2 ، u (V_ {k-1})) ، V_ {k-1})$$

للحصول على الدفق البصري نفسه ، نضيف ببساطة الشبكة المسند وزيادة الدفق من المستوى السابق:

$$

$$V_k = u (V_ {k-1}) + v_k.$$

للحصول على Ground Truth للشبكة على هذا المستوى ، نحتاج إلى القيام بالعملية المعاكسة - طرح المسند من الهدف (خفض إلى المستوى المطلوب) من المستوى السابق للهرم. بشكل تخطيطي ، يبدو كما يلي:



ميزة هذا النهج هو أنه يمكننا تدريس كل مستوى بشكل مستقل. بدأ المؤلفون التدريب من المستوى 0 ، وتم تهيئة كل شبكة تالية باستخدام معلمات الشبكة السابقة. منذ كل شبكة $$$G_i$يحل المشكلة أبسط بكثير من الحساب الكامل للتدفق البصري في صورة كبيرة ، ثم يمكن جعل المعلمات أقل بكثير. لدرجة أن المجموعة بأكملها الآن يمكن أن تناسب الأجهزة المحمولة:



المجموعة نفسها هي كما يلي (مثال على هرم من 3 مستويات):



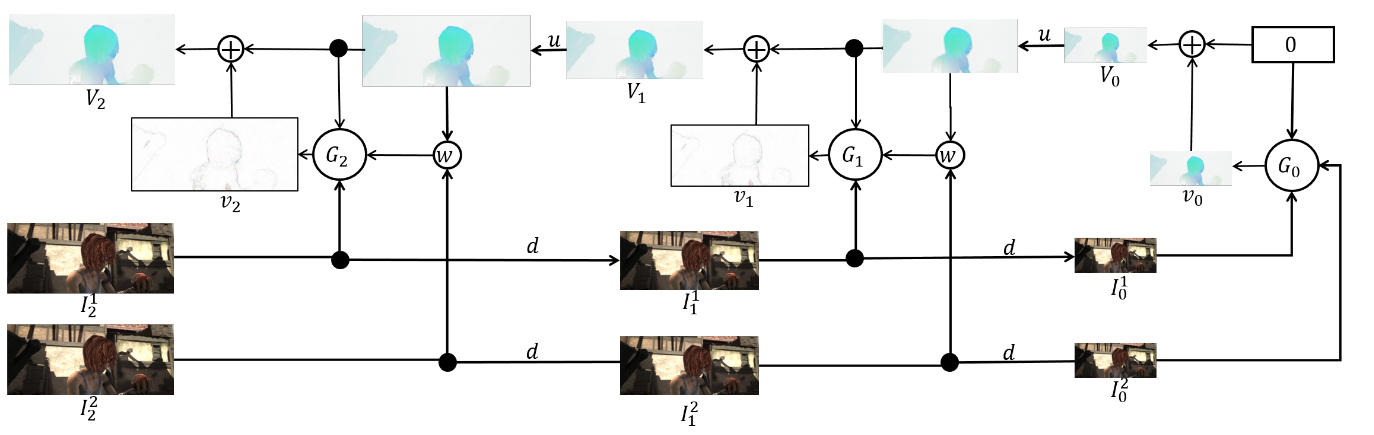
يبقى أن نتحدث مباشرة عن الهندسة المعمارية $$$G_i$الشبكة وتأخذ الأسهم. كل شبكة $$$G_i$يتكون من 5 طبقات تلافيفية ، تنتهي كل منها بتنشيط ReLU ، باستثناء الأخيرة (التي تتوقع التدفق البصري). عدد المرشحات في كل طبقة على التوالي { $$ }. مدخلات الشبكة العصبية (الصورة ، الصورة الثانية "ملفوفة" في الدفق البصري والدفق البصري نفسه) متسلسلة ببساطة من خلال البعد الخاص بالقنوات ، لذلك يحتوي موتر الإدخال على 8. النتائج مثيرة للإعجاب:

PWC-Net (2018)

بناءً على نجاح زملائهم الألمان ، قرر شباب NVIDIA تطبيق خبراتهم (وبطاقات الفيديو) لزيادة تحسين النتيجة. استند عملهم إلى حد كبير على أفكار من النموذج السابق (SpyNet) ، لذلك ستتعامل PWC-Net أيضًا مع الأهرامات ، ولكن مع أهرامات الإلتواء ، وليس الصور الأصلية ، مرة أخرى - بالترتيب.

إن استخدام شدة البكسل الخام لحساب التدفق البصري أمر غير معقول دائمًا ، لأنه سيؤدي التغيير الحاد في السطوع / التباين إلى كسر افتراضنا بأن البيكسلات تنتقل من إطار إلى آخر بدون تغييرات ولن تكون الخوارزمية مقاومة لهذه التغييرات. في الخوارزميات الكلاسيكية لحساب التدفق البصري ، يتم استخدام تحويلات مختلفة للتخفيف من هذا الموقف ، وفي هذه الحالة ، قرر المؤلفون تزويد النموذج بفرصة لتعلم مثل هذه التحولات بأنفسهم. لذلك ، بدلاً من هرم الصور في PWC-Net ، يتم استخدام أهرامات الالتفاف (ومن هنا جاءت الحرف الأول في Pwc-Net) ، أي مجرد ميزة خرائط من مختلف طبقات CNN ، والذي يسمى مستخرج هرم الميزة هنا.

بعد ذلك ، يبدو كل شيء تقريبًا في SpyNet ، قبل التقديم مباشرة إلى CNN ، والذي يسمى مقدّر التدفق البصري ، كل ما تحتاجه ، وهو:

• صورة (في هذه الحالة ، خريطة المعالم من مستخرج هرم المعالم) ،
• التدفق البصري لأعلى العينات المحسوب في المستوى السابق ،
• الصورة الثانية ، "ملفوفة" (تذكر طبقة التزييف ، وبالتالي الحرف الثاني في pWc-Net) في هذا الدفق البصري ،

بين الإطار الثاني "الملفوف" والإطار الأول المعتاد (مرة أخرى ، أذكر أنه بدلاً من الصور الأولية ، يتم استخدام بطاقات الميزات مع مستخرج هرمي للميزات هنا) النظر في ما يسمى حجم التكلفة (وبالتالي الحرف الثالث في pwC-Net) والذي هو بالفعل بالفعل نظرت سابقا العلاقة بين صورتين.



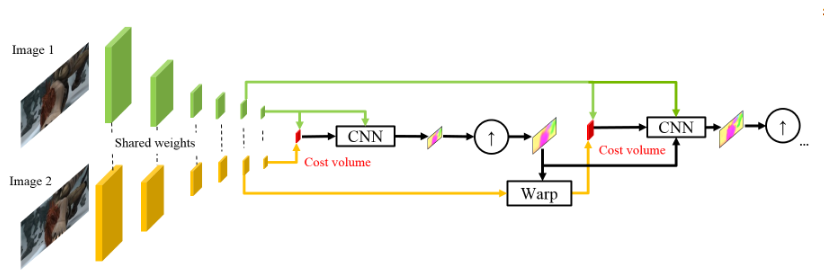
اللمسة الأخيرة هي شبكة السياق ، التي تتم إضافتها مباشرة بعد مقدّر التدفق البصري وتلعب دور المعالجة اللاحقة المدربة للتيار البصري المحسوب. يمكن الاطلاع على التفاصيل المعمارية تحت المفسد أو في المقالة الأصلية.


النتائج أكثر إثارة للإعجاب:



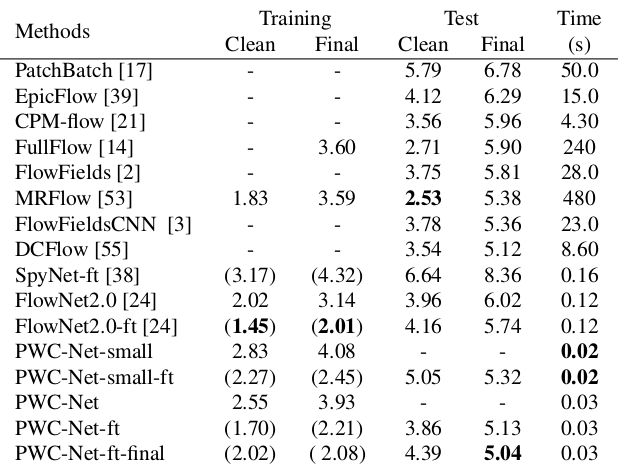
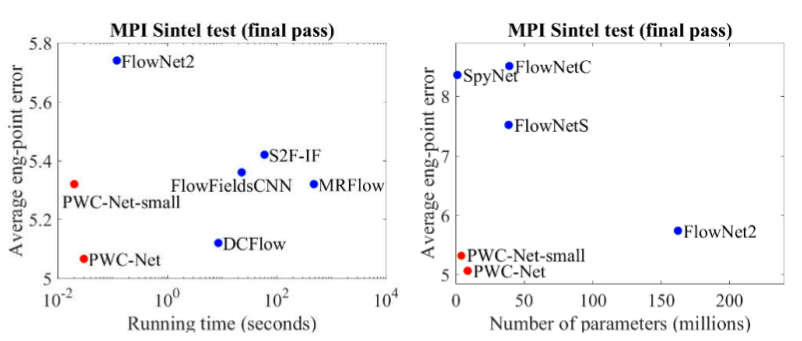
مقارنة بطرق CNN الأخرى لحساب التدفق البصري ، تحقق PWC-Net توازنًا بين الجودة وعدد المعلمات:



هناك أيضًا عرض تقديمي ممتاز للمؤلفين أنفسهم ، حيث يتحدثون عن النموذج نفسه وتجاربهم:

استنتاج

يعد تطور البنى التي تحل مشكلة عد التدفق البصري مثالاً رائعًا على كيف أن التقدم في بنيات CNN والجمع بينها وبين الأساليب الكلاسيكية يعطي أفضل النتائج وأفضلها. وعلى الرغم من أن أساليب السيرة الذاتية الكلاسيكية لا تزال تفوز بالجودة ، فإن النتائج الحديثة تمنح الأمل في أن هذا قابل للتثبيت ...

المصادر والروابط

1. FlowNet: تعلم التدفق البصري مع الشبكات التلافيفية: المادة ، الكود .
2. التدفق البصري للإزاحة الكبيرة: مطابقة الواصف في تقدير الحركة التباينية: مقالة .
3. تقدير التدفق البصري باستخدام شبكة الهرم المكاني: مقال ، كود .
4. PWC-Net: CNNs للتدفق البصري باستخدام الهرم والتزييف وحجم التكلفة: المادة ، الكود .
5. ما تريد معرفته عن التدفق البصري ، لكنك شعرت بالحرج من السؤال: مقالة .
6. حساب التدفق البصري بطريقة لوكاس كندا. النظرية: مقالة .
7. قالب مطابقة مع OpenCVP: قفص الاتهام .
8. كوو فاديس ، الاعتراف بالعمل؟ نموذج جديد ومجموعة البيانات الحركية: مقالة .
9. FlowNet 2.0: تطور تقدير التدفق البصري مع الشبكات العميقة: المادة ، الكود .