👩🏻‍🤝‍👨🏾 👨🏻‍🎤 👨‍❤️‍💋‍👨 أسهل قناة MIMO تقريبًا مع تلاشي (نموذج Kronecker متضمن) ⛹🏼 💃🏻 👛

يوم جيد للجميع!

بالنظر إلى موضوع التنوع المكاني ، لقد تطرقنا بالفعل إلى كل من قضايا الخبو في قنوات الاتصال ولماذا يحدث هذا الخبو. أقترح اليوم التحدث عن هذا الموضوع بمزيد من التفصيل.

علاوة على ذلك ، في مقال اليوم ، سنتطرق قليلاً إلى مسائل الارتباط المكاني لقنوات MIMO ، والتي تتم مناقشتها تقليديًا في سياق دورة الاتصالات المتنقلة ( CSP ) للأستاذ هاردت ، وبالتالي ، في رأيي ، لن يكون هذا المنشور غير ضروري. وألاحظ على الفور ، أن مجموعة المشكلات لا تقتصر على استخدامها فقط في الاتصالات المتنقلة.

بشكل عام ، أدعو جميع المهتمين بموضوع الاتصالات اللاسلكية إلى القراءة ، ودعنا نذهب!

كولين سلاتر "ذكريات باهتة" . نعم ، ربما يكون الحد من كل شيء إلى موضوع واحد أمرًا مبالغًا فيه ، ولكن مع بعض الاستعارات ، أعتقد أنه يمكنك تخيل ما يتلقاه المستقبل بعد كل أنواع التأثيرات على إشارة المعلومات الأصلية ...

عن ماذا نتحدث؟

لنبدأ بحقيقة أنه يوجد في الطبيعة ما يسمى بالضوضاء المضاعفة التي تؤثر على قدرة الإشارة المستقبلة - الخبو .

المصطلحات ، كما قد تفكر ، ليست مترجمة مباشرة باللغة الروسية والإنجليزية ، لكن هذا ليس مهمًا جدًا.

في الأدب الإنكليزي ، يشير مصطلح الخبو إلى تأثير معين ، والذي ، كما كان ، يؤدي إلى تلاشي الإشارة إلى "التلاشي".

في أدبنا ، يستخدم مصطلح الخبو عادةً ، وهذا يرجع في المقام الأول إلى تأثير المسيرات المتعددة: إذا واجهت الموجة الكهرومغناطيسية نسختها الناتجة عن الانعكاسات والانعراج ، وكانت في الطور المضاد ، فإن الأمواج ستلغي بعضها البعض - أي القناة ، كما كان ، يتجمد .

يتلاشى سريع وبطيء (يتلاشى سريع وبطيء ).

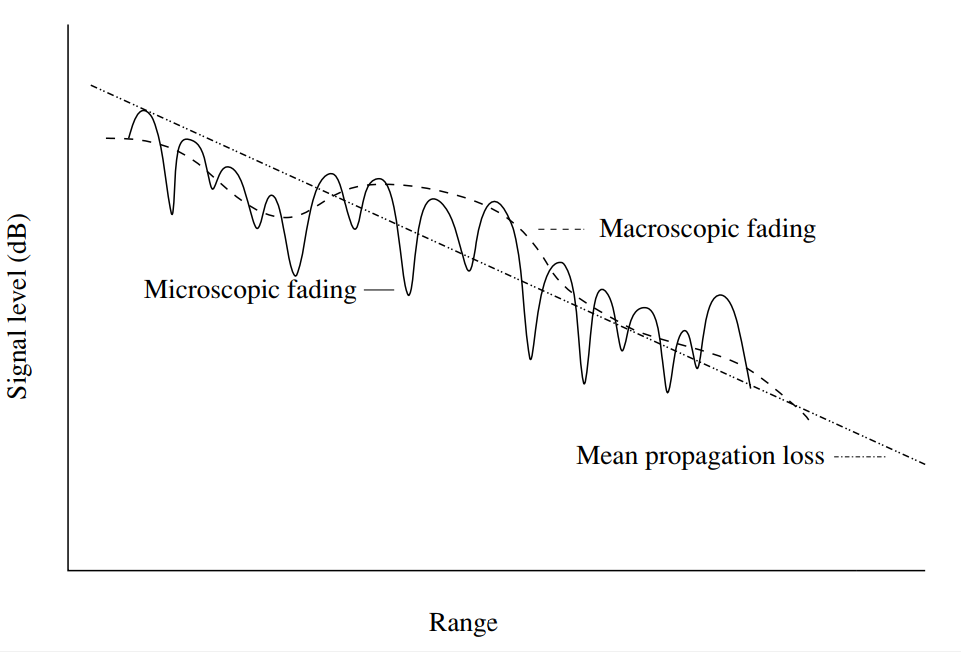
التين. 1. تقلبات في إشارة السلطة في القنوات اللاسلكية اعتمادا على المسافة. يزيد متوسط مستوى خسارة الانتشار رتابة مع زيادة المدى. يمكن أن تحدث الانحرافات المحلية بسبب التلاشي المجهري (البطيء) والمجهر (سريع) [1 ، صفحة 14].

أعترف على الفور ، اليوم لن نعمل مع تلاشي بطيء ، لكننا سنتحدث عن الصيام بتفاصيل كافية.

التين. 2. رسم توضيحي لتأثير التظليل: كقاعدة عامة ، يحدث تلاشي بطيء بسبب التظليل (التظليل). للمحاكاة ، عادة ما يتم اختيار التوزيع اللوغاريتمي .

إذا كنت ترغب في قراءة القليل عن الخبو البطيء ، على وجه الخصوص ، وكيف يمكنك محاكاة القنوات الفضائية ، بشكل عام ، أدعوك هنا !

يتلاشى بسرعة

يحدث التلاشي السريع ، كقاعدة عامة ، لسببين رئيسيين:

بسبب انتشار المسيرات المتعددة التي ذكرناها بالفعل و / أو
بسبب التحولات تردد دوبلر .

وهذه الأخيرة ملحوظة للغاية بالنسبة للأنظمة الساتلية ، ولكنها لا تؤخذ دائمًا في الاعتبار لحالات الاتصالات الأرضية بسبب حقيقة أن المحطات الأساسية في هذه الحالة تكون ثابتة عادة.

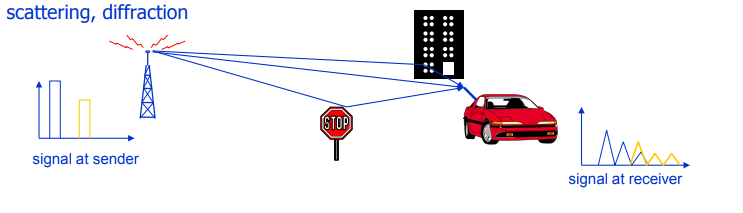
التين. 3. توضيح أسباب يتلاشى. يتم إيلاء اهتمام خاص للتشتت والحيود: ويرجع السبب في هذه الظاهرة بالتحديد إلى ما يسمى بالانتشار المتعدد المسيرات ، مما يؤدي إلى التداخل بين الرموز ( ISI ).

لكن هذا أبعد ما يكون عن الكل.

خبو انتقائي مقابل يتلاشى شقة

أعلاه ، قمنا بتقسيم تدخلنا حسب طبيعة الحدوث . ومع ذلك ، يمكن تقسيم التداخل أيضًا حسب طبيعة التأثير على الإشارة المرسلة . وهنا نحتاج إلى مفهوم انتقائية القناة.

نعطي تصنيفًا صغيرًا وفقًا لـ [1 ، ص. 14-18]. لذلك ، يمكن أن يكون التلاشي السريع:

انتقائي (انتقائية)
أ. تردد انتقائي
ب. انتقائي الوقت المجال (انتقائية الوقت)
في. انتقائي من الناحية المكانية (يتعلق الأمر بمسألة زوايا وصول ومغادرة موجات EM - لن نحلل هذه المشكلة اليوم)
مسطحة - تنجذب أكثر إلى طبيعة الخبو البطيء (نعم ، هذه مفارقة)

ما يوحي المصطلح الأخير هو موضح من العكس.

أولاً ، إذا كان عرض طيف الإشارة المرسلة من قبلنا يتجاوز عرض النطاق التماسكي للقناة ، فإنهم يقولون أننا نتعامل مع التداخل الانتقائي للترددات.

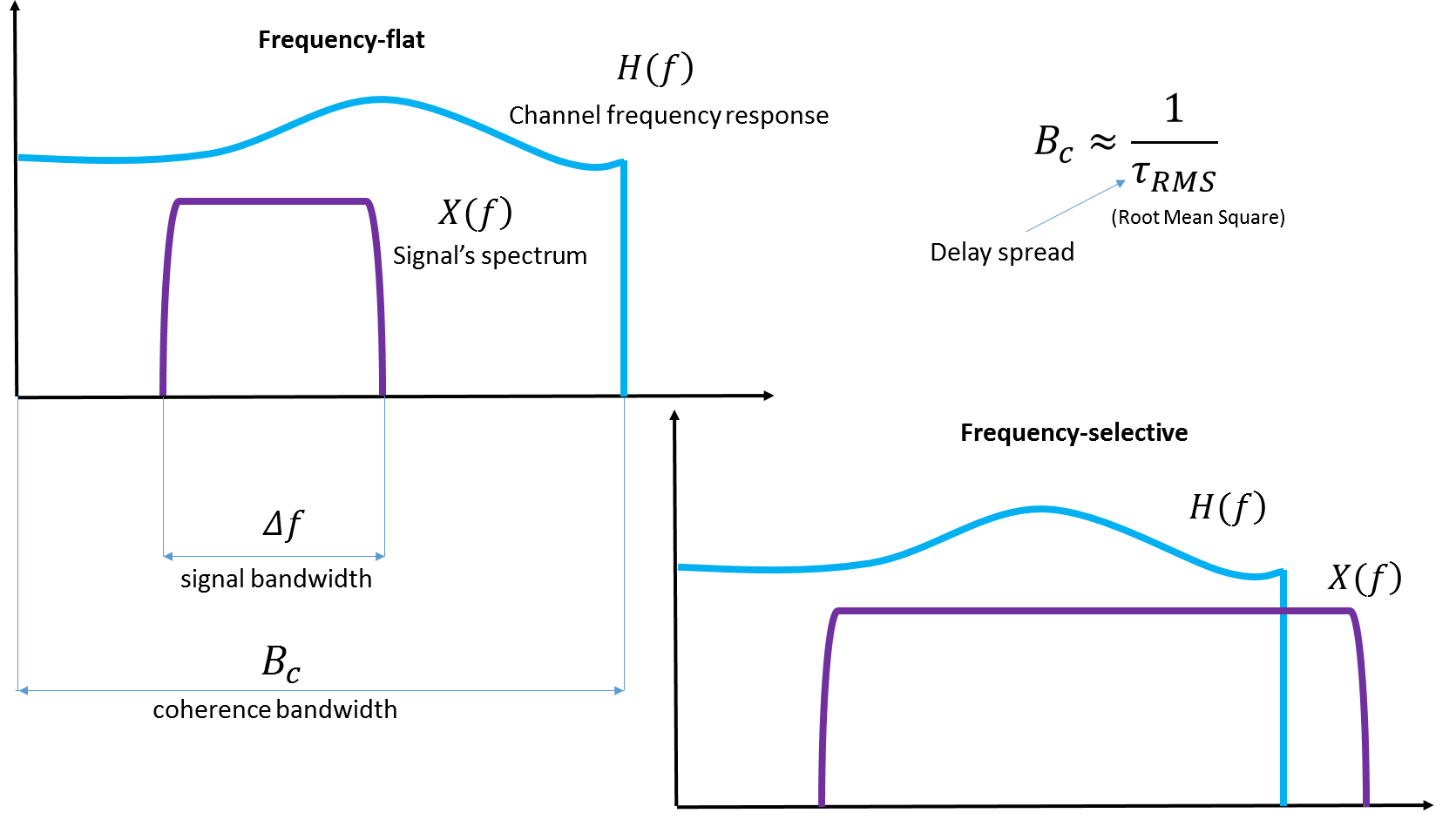
التين. 4. التوضيح من عرض النطاق الترددي متماسك. أعتقد أنها لن تكون فكرة سيئة إرفاق الرسوم التوضيحية من ويكي ، إذا كان هو نفسه أضافهم هناك.

إيلاء الاهتمام لمتغير تأخير انتشار - انتشار التأخير. هذا هو الفرق في التأخير بين وصول نسخ مختلفة من نفس الإشارة التي يتم قياسها عند تحديد خصائص قناة حقيقية معينة.

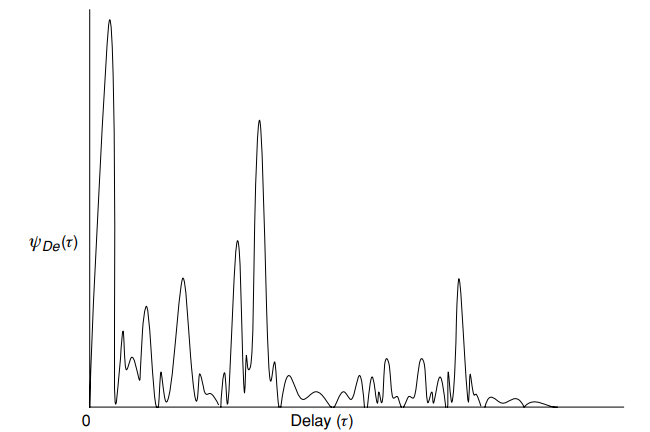
التين. 5. نموذجي التأخير (الطاقة) $\ psi_ {De} (\ tau)$ - متوسط القوة كدالة تأخير $\ تاو$ . [1 ، ص. 16]

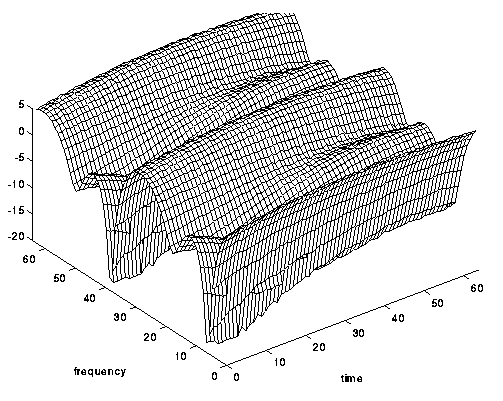
التين. 6. تردد انتقائية ، ولكن ليس قناة انتقائية للوقت .

لكل نطاق ، سيكون النطاق المتماسك مختلفًا.

على سبيل المثال ، بالنسبة إلى النطاق S (كنت مهتمًا عندما كنت أبحث عن معلومات حول أنظمة الأقمار الصناعية) Bc = 0.5 - 2 MHz (Kanatas AG ، Panagopoulos AD (ed.). انتشار الموجات الراديوية ونمذجة القنوات للأرض - أنظمة الفضاء. - CRC Press ، 2016 - ص 107).

هذا يناسب بشكل جيد في معدل باود ، على سبيل المثال ، مثل جهاز الإرسال والاستقبال الفضائية . وليس هناك ما يثير الدهشة: يتزامن معدل رمز الأنواع الخطية للتشكيل الرقمي (PSK ، QAM ، OFDM) مع النطاق الذي تشغله الإشارة (انظر Goldsmith A. الاتصالات اللاسلكية - جامعة ستانفورد ، 2004. - ص 140 ، 326) ، مما يعني سيكون من الجيد محاولة الضغط على الإشارة في النطاق المتماسك إلى الحد الأقصى. ترددات لا تزال موردا قيما.

ثانياً ، إذا تجاوز طول إشارة لدينا في المجال الزمني وقت تماسك القناة ، فإنهم يقولون إننا نتعامل مع قناة تختلف في الوقت المناسب.

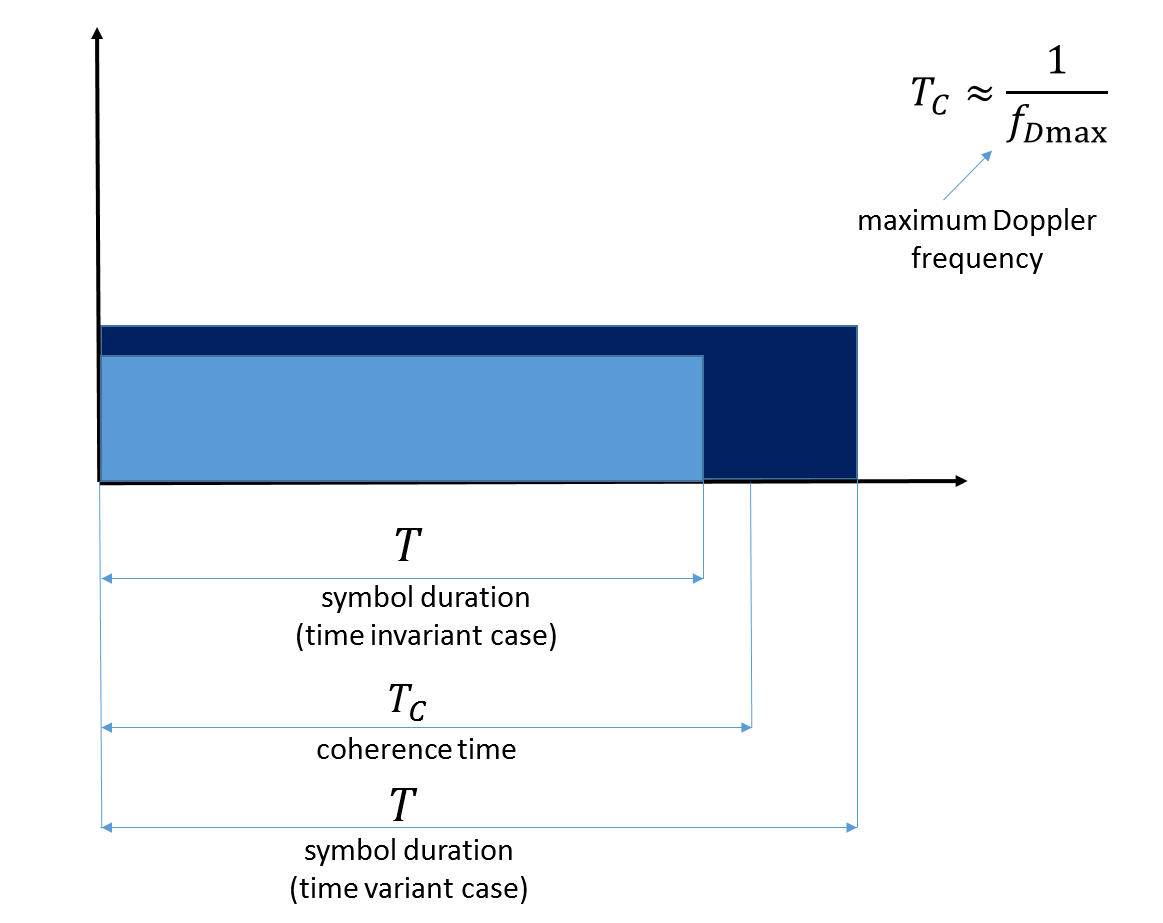
التين. 7. التوضيح من التماسك الوقت. يرجى ملاحظة أن الحد الأقصى لتردد دوبلر يعكس حركة المحطة المتنقلة نفسها.

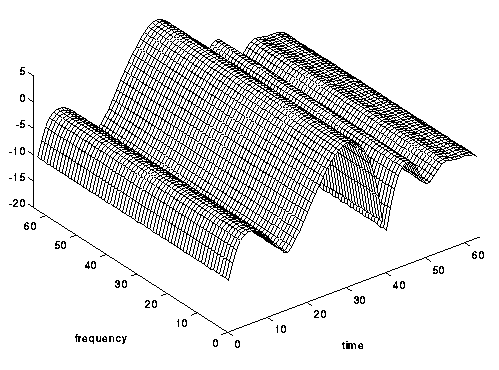
التين. 8. تقريبًا غير مرئي ، لكن انتقائي للوقت: قناة سريعة التحلل.

في الحياة الحقيقية ، للأسف ، يجب على المرء أن يتوقع كلاهما.

قناة رايلي المنتقاة للوقت والانتقائية للتردد ؛ "الوضع الحقيقي."

مصدر التوضيح: تقنية جيجابت اللاسلكية

حسنًا ، ووفقًا لذلك ، إذا تمكنا من تجنب ما سبق ، فإننا سنصل إلى أبسط الحالات وأكثرها ملاءمة - التلاشي المسطح [1 ، ص. 14-18] [2 ، ص. 88-92].

أسهل قناة يتلاشى

ربما تكون قد شاهدت بالفعل طريقة مماثلة لمحاكاة قناة مسطحة مع التلاشي في مكان ما:

h = (1/sqrt(2))*(randn(size(msg)) + 1j*randn(size(msg))) % MatLab / Octave

ما المقصود:

الافتقار إلى خط البصر (حالة مبررة للاتصالات الأرضية)
قناة ضيقة النطاق (قناة ضيقة النطاق) - تنسجم مع النطاق المتماسك
- بالمناسبة ، درسنا مثالًا لقناة النطاق العريض في هذه المقالة (الشكل 4).
لا توجد انتقائية تردد إما - تنسجم مع الوقت المتماسك
عدم وجود تظليل وتحولات تردد دوبلر

وهذا هو ، هنا شخصيا: قناة مسطحة مع يتلاشى . لحالة دون خط البصر ، وتسمى القناة أيضا رايليغ .

اللورد رايلي

ماذا يأتي هذا النموذج من؟

أولاً ، عند الحديث عن أنظمة الاتصالات الحديثة ، فإننا نعني على الأرجح العمل مع الإشارات الرقمية. علاوة على ذلك ، نحن نعمل أيضًا على الأرجح مع أنواع التربيع من التعديل ( I / Q ) ، أي مع إشارات معقدة.

التين. 9. كوكبة إشارة QPSK . الإحداثيات القطبية ، دائرة الوحدة. على سبيل المثال ، سيتوافق الرمز 11 مع إحداثي يساوي 0.7 + 0.7i تقريبًا .

من المنطقي افتراض تأثير التداخل على كل من المكون الحقيقي والخيالي. علاوة على ذلك ، يجدر باتباع نظرية الحد المركزي أن نفترض أيضًا الطبيعة الغوسية لمثل هذه الآثار. نكتب الصيغة [1 ، ص. 39]:

$Z = X + jY \ qquad (1)$

حيث $X \ sim \ mathcal {N} (0 ، \ ، \ sigma ^ 2)$ و $Y \ sim \ mathcal {N} (0 ، \ ، \ sigma ^ 2)$ يتم توزيعها عادة متغيرات عشوائية.

في أغلب الأحيان ، يتم استخدام نموذج بقدرة متوسطة طبيعية:

$var \ {Z \} = E \ {\ left | Z \ right | ^ 2 \} = 1 \ qquad (2)$

وهذا يعني $Z \ sim \ mathcal {N} (0 ، \ ، 1)$ .

إذا افترضنا تشوهات مستقلة لمكونات غلاف الإشارة: في كل من الطور ( I - في الطور) والتربيع ( Q - التربيع) ، فإن موقع الرقم الذي سيتم به ضرب الرمز الأصلي (ومن ثم الضوضاء المتعددة ) ، في الإحداثيات القطبية تحسب حرفيا بواسطة نظرية فيثاغورس:

$Z = \ sqrt {\ hat {X} ^ 2 + \ hat {Y} ^ 2} \ qquad (3)$

حيث $\ hat {X} \ sim \ mathcal {N} (0، \، \ sigma ^ 2)$ و $\ hat {Y} \ sim \ mathcal {N} (0، \، \ sigma ^ 2)$ - يتم أيضًا توزيع هذه المتغيرات العشوائية بشكل طبيعي. للحصول على قوة في التصنيف $\ hat {X} \ sim \ mathcal {N} (0، \، 1)$ . $\ hat {Y} \ sim \ mathcal {N} (0، \، 1)$ .

وهنا لدينا صيغة عملية رايليغ ! [2 ، ص 78]

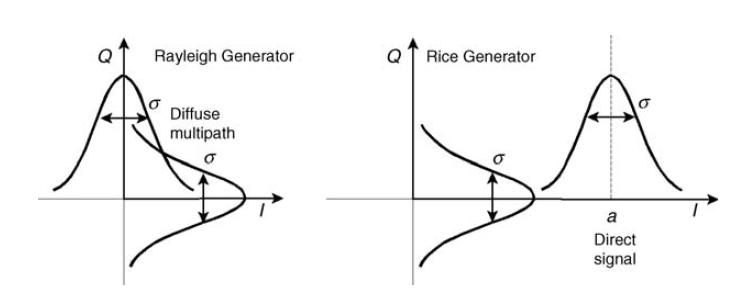
التين. 10. مولدات غاوس التربيعية لنمذجة رايلي ورايس تتلاشى [3 ، صفحة 125]. سنتحدث عن قناة رايس لاحقًا.

انحدار غنائي.

شخصياً ، أحب حقًا مثال رؤية البندقية : إذا أطلقت مدفعتان النار عموديًا على بعضهما البعض عدة مرات ، فسيكون توزيع الضربات طبيعيًا لكل فرد على حدة ، ويكون التوزيع الكلي للضربات هو رايلي. شيء مماثل يحدث مع تدخلنا.

إذا نظرنا إلى أبسط الحالات دون أي ارتباط مكاني بين القنوات (دعنا نقول أن لدينا العديد من القنوات المكانية - MIMO ) ، فإنهم يقولون إن القناة بيضاء مكانية - بيضاء مكانية . ونظرًا لأن جميع القنوات مستقلة ، فمن الممكن "توليد" المتغيرات العشوائية الموزعة وفقًا لرايلي فقط ، ولكن أيضًا المتجهات والمصفوفات والتنسورات [3 ، الصفحة 125]:

$\ mathbf {H} _ {NLoS} = \ sqrt {\ frac {1} {2}} \ left (\ mathbf {G} _1 + j \ mathbf {G} _2 \ right) \ qquad (4)$

حيث $\ mathbf {G} _1 \ sim \ mathcal {N} (0، \، 1)$ و $\ mathbf {G} _2 \ sim \ mathcal {N} (0، \، 1)$ هي المصفوفات التي تتكون من القيم الموزعة عادة.

من أين جاء 1/2 من تحت الجذر؟

كل شيء بسيط هنا: كما ذكرنا أعلاه ، يجب أن تكون قوة استجابة القناة مساوية للوحدة ، أي:

$P = E \ {hh ^ * \} = 1$

ولهذا السبب يتم تقديم عامل التحجيم $\ sqrt {\ frac {1} {2}}$ .

إظهار (خذ الثعبان للتغيير):

 import numpy as np N = int(1e6) h = 1/np.sqrt(2)*(np.random.randn(N) + 1j*np.random.randn(N)) P = np.mean(h*np.conj(h)) print(np.round(P)) >>> (1+0j)

لتلخيص :
يمكن وصف مكون التداخل في حالة عدم وجود رؤية مباشرة بأنه متجه n- الأبعاد (اعتمادًا على بعد القناة) مستقل الموزع بشكل متماثل ( IID - مستقل متماثل الموزع) وفقًا للقانون الغوسي المعقد مع تناظر دائري وصفر حصيرة. التوقع ( ZMCSCG - صفر يعني مجمع غاوسي متماثل دائري).

الاعصار اللسان كله!

تقريبا أسهل قناة يتلاشى

حسنا ، ماذا لو كان لا يزال هناك وضوح مباشر؟ ربما هناك بالفعل نماذج رياضية جاهزة في هذه النتيجة؟

بالطبع هناك! على سبيل المثال ، تم تعميم هذا [4] للحالة مع العديد من هوائيات الاستقبال والإرسال (MIMO):

$\ mathbf {H} = \ sqrt {\ frac {K} {K + 1}} \ mathbf {H_ {LoS}} + \ sqrt {\ frac {1} {K + 1}} \ mathbf {H_ {NLoS} } \ qquad (5)$

حيث $$ \ mathbf {H}$ - هذا هو في الواقع المغلف المعقد للاستجابة النبضية للقناة (أو مصفوفة القناة ، إذا كنا نتحدث عن MIMO ) ، $$ \ mathbf {H_ {LoS}}$ هو عنصر الرؤية المباشرة (خط البصر) ، و $\ mathbf {H_ {NLoS}}$ - هذا عنصر من عناصر عدم وضوح الرؤية المباشرة (بدون خط البصر) ، لقد فكرنا فيه بالفعل.

لاحظ المتغير K - وهو ما يسمى عامل Ricean (عامل Rician / Ricean) - نسبة قدرة مسار الانتشار المباشر إلى قدرة جميع المسارات الأخرى. هو الذي يحدد مقدار قناتنا التي ستخضع للتدخل.

ستيفن أو. "ستيف" رايس

summand $\ sqrt {\ frac {K} {K + 1}} \ mathbf {H} _ {LoS} = E \ {H \}$ يمثل التوقع الرياضي لمصفوفة القناة ويمكن نمذجه على أساس هندسة مصفوفات الاستقبال والإرسال للهوائيات:

$\ mathbf {H} _ {LoS} = \ mathbf {a} _R (\ theta_R) \ mathbf {a} _T (\ theta_T) ^ H \ qquad (6)$

حيث $\ mathbf {a} _R (\ theta_R)$ و $\ mathbf {a} _T (\ theta_T)$ - هذه هي استجابات صفيفات الاستقبال والإرسال للهوائيات ، على التوالي ، و $\ theta_R$ و $\ theta_T$ هي زوايا الوصول والمغادرة (زاوية المغادرة).

العوامل متماثلة بشكل عام ويمكن وصفها بالصيغة العامة:

$\ mathbf {a} = \ left [1، e ^ {j2 \ pi d cos (\ theta)}، ...، e ^ {j2 \ pi d (N-1) cos (\ theta)} \ right] \ qquad (7)$

حيث $د$ هي المسافة بين الهوائيات (تباعد الهوائي) بأطوال موجية ، و $N$ - هذا هو عدد العناصر في صفيف الهوائيات (الشكل 11).

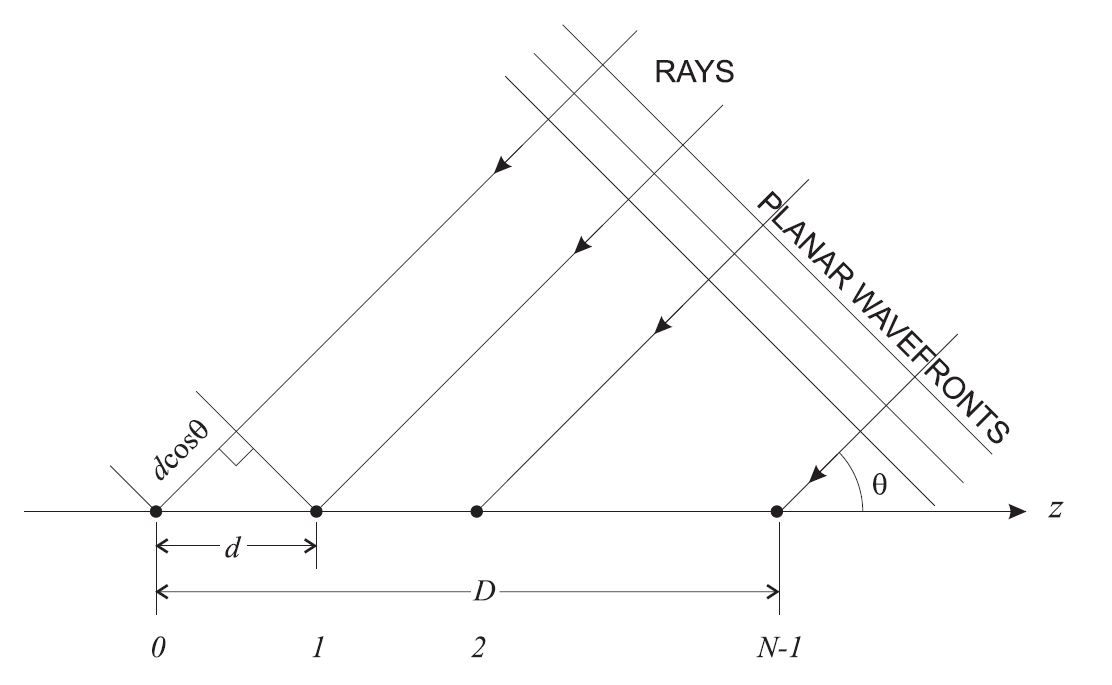
التين. 11. هندسة مجموعة خطية . بالنسبة لـ Massive MIMO ، فإن الهندسة ، بالطبع ، ستكون مختلفة. يمكنك قراءة المزيد حول هذا الموضوع ، على سبيل المثال ، هنا .

حسنًا ، الآن بعد تفكيك النموذج على الأقل إلى حد ما ، يمكنك تبسيطه.

بالنسبة لحالة SISO (أبسط والأكثر أساسية) ، فإن الصيغة (5) تأخذ الشكل:

$h = \ sqrt {\ frac {K} {K + 1}} + \ sqrt {\ frac {1} {2 (K + 1)}} \ left (G_1 + jG_2 \ right) \ qquad (8)$

لمدة 1 الإرسال و 1 هوائي الاستقبال $\ mathbf {a} _T (\ theta_T) \ mathbf {a} _R (\ theta_R) = 1$ .

وهذا ، بالمناسبة ، يناسب النموذج في الشكل 12.

مخطط

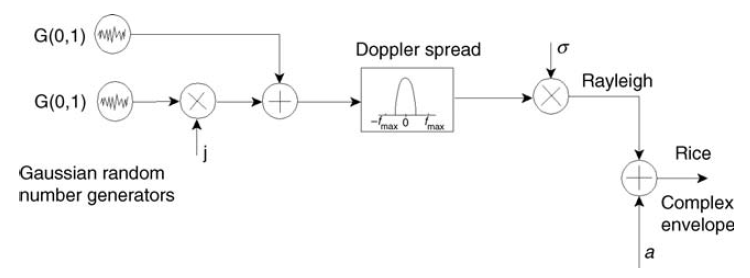
التين. 12. مخطط تشكيل قناة رايس (إشارة ضيقة النطاق) [3 ، صفحة 127]. في $K \ إلى 0$ سوف تتدهور القناة أكثر فأكثر إلى رايلي. لهذا السبب استخدمت الكلمة في العنوان الفرعي تقريبًا: قناة رايلي هي حالة خاصة لقناة رايس. وينظر إلى هذا أيضًا من الصيغة (5).

دعنا نوضح: $\ sigma = \ sqrt {\ frac {1} {2 (K + 1)}}$ هي المعلمة مقياس Rician ، و $a = \ sqrt {\ frac {K} {K + 1}}$ هي معلمة اللامركزية.

إذا أخذنا في الاعتبار الخبو المسطح ، فمن المفترض أن كتلة انتشار دوبلر لها استجابة 1.

بشكل عام ، لغرض نمذجة Doppler Spread ، على الأرجح سوف تصادف نموذج Jakes (شكل U) يعتمد على تقنية Sum-of-sinusoids . من الناحية النظرية ، يبدو طيف هذا النموذج كما يلي:

الكثافة الطيفية للقدرة لتوهين رايلي مع أقصى تحول دوبلر قدره 10 هرتز. مصدر .

ومع ذلك ، في الحياة ، إذا حكمنا من خلال [1 ، ص. 15] لا يزال هذا الطيف يبدو أقل:

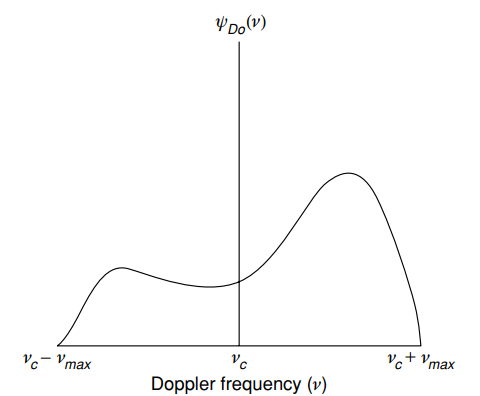
طيف دوبلر نموذجي (الطاقة) $\ psi_ {Do} (v)$ - متوسط القدرة كدالة لتردد دوبلر $(V)$ [1 ، ص. 15].

التوقعات ... الواقع.

هناك مثل هذه المخططات للاندماج مع الخبو البطيء.

على سبيل المثال ، هذا طراز Corazza-Vatalaro (C & V) :

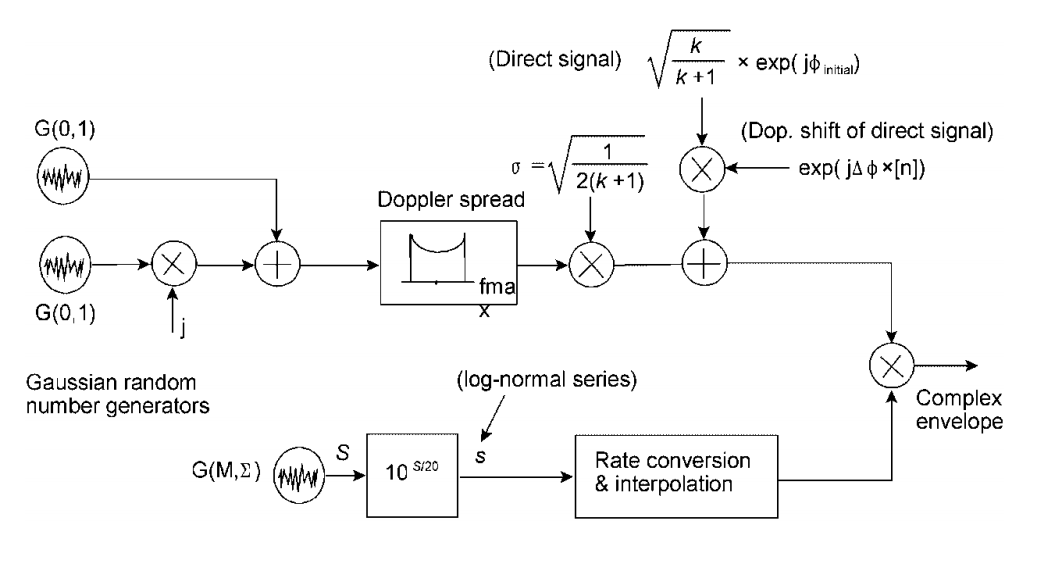
انظر Fontan، FP، Mayo، A.، Marote، D.، Prieto - Cerdeira، R.، Mariño، P.، Machado، F.، & Riera، N. (2008). استعراض النماذج التوليفية لقناة الانتشار الساتلية المتنقلة البرية ضيقة النطاق. المجلة الدولية للاتصالات الساتلية والشبكات ، 26 (4) ، 291-316.

لكن هذه قصة مختلفة تماما ...

نمذجة ما يقرب من أسهل قناة يتلاشى في MatLab

دعونا نقارن الحسابات المستلمة بشيء تم التحقق منه بالفعل. على سبيل المثال ، مع وظائف MatLab الخاصة .

لاختبار النموذج ، من جانبنا ، نقوم بإنشاء رسالة ثنائية عشوائية (يبلغ طول الرسالة 100000 بت) ، ونعدلها باستخدام M-PSK أو M-QAM ، اضرب عنصرًا حسب العنصر في عملية الخبو ، أضف ضوضاء غوسية بيضاء ، ونوازن معادل التأثير الجبري ونزع التشكيل وحساب نسبة الخطأ في البتات (نسبة الخطأ في البتات إلى الخطأ في البتات) (الشكل 13). عدد الاختبارات سيكون مساويا لمائة.

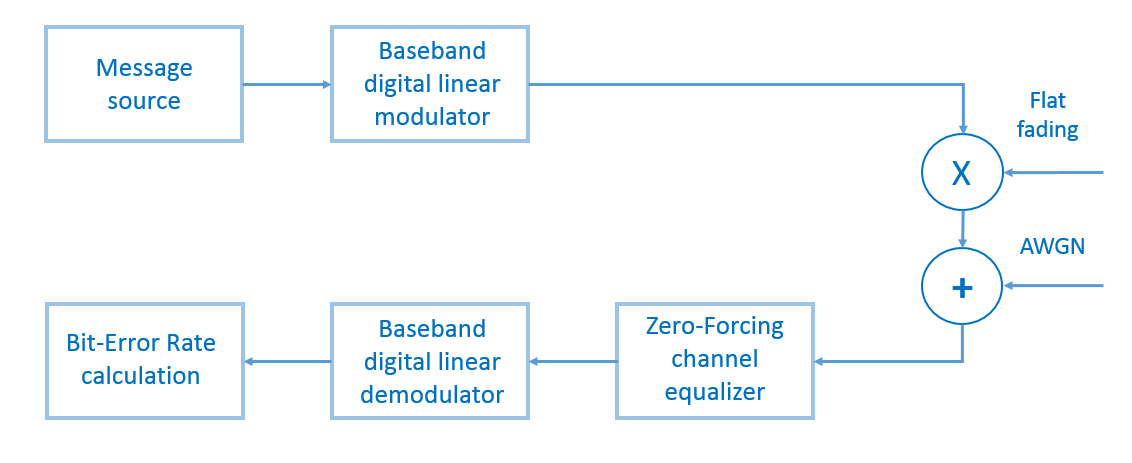
الشكل 13. مخطط كتلة نموذج نظام النقل الذي سيصفه نصنا.

يمكن الاطلاع على البرنامج النصي هنا.

وتنزيل هنا .

 clear all; close all; clc EbNo = 0:40; K = [4.0; 0.6]; M = [4; 8; 16; 64; 256]; %Positions of modulation (M-PSK or M-QAM) for k = 1:length(K) for m = 1:length(M) message = randi([0, M(m)-1], 100000, 1); if M(m) >= 16 mod_msg = qammod(message, M(m), pi/4, 'gray'); ric_ber(:, m, k) = berfading(EbNo,'qam',M(m),1,K(k)); else mod_msg = pskmod(message, M(m), pi/4, 'gray'); ric_ber(:, m, k) = berfading(EbNo, 'psk', M(m), 1, K(k)); end Es = mean(abs(mod_msg).^2); No = Es./((10.^(EbNo./10))*log2(M(m))); h = sqrt( K(k)/(K(k)+1)) +... sqrt( 1/(K(k)+1))*(1/sqrt(2))*(randn(size(mod_msg))... + 1j*randn(size(mod_msg))); ric_msg = mod_msg.*h; % Rician flat fading for c = 1:100 for jj = 1:length(EbNo) noisy_mod = ric_msg +... sqrt(No(jj)/2)*(randn(size(mod_msg))+... 1j*randn(size(mod_msg))); %AWGN noisy_mod = noisy_mod ./ h; % zero-forcing equalization if M(m) >= 16 demod_msg = qamdemod(noisy_mod, M(m), pi/4, 'gray'); else demod_msg = pskdemod(noisy_mod, M(m), pi/4, 'gray'); end [number,BER(c,jj)] = biterr(message,demod_msg); end end sum_BER(:,m, k) = sum(BER)./c; end end figure(1) semilogy(EbNo, sum_BER(:,1,1), 'b-o', EbNo, sum_BER(:,2,1), 'r-o',... EbNo, sum_BER(:,3,1), 'g-o', EbNo, sum_BER(:,4,1), 'c-o',... EbNo, sum_BER(:,5,1), 'k-o',... EbNo, ric_ber(:,1,1), 'b-', EbNo, ric_ber(:,2,1), 'r-',... EbNo, ric_ber(:,3,1), 'g-', EbNo, ric_ber(:,4,1), 'c-',... EbNo, ric_ber(:,5,1), 'k-', 'LineWidth', 1.5) title('Rician model (K = 4.0)') legend('QPSK(simulated)', '8-PSK(simulated)',... '16-QAM(simulated)', '64-QAM(simulated)' ,'256-QAM(simulated)',... 'QPSK(theory)','8-PSK(theory)', '16-QAM(theory)',... '64-QAM(theory)' ,'256-QAM(theory)','location','best') xlabel('EbNo (dB)') ylabel('BER') grid on figure(2) semilogy(EbNo, sum_BER(:,1,2), 'b-o', EbNo, sum_BER(:,2,2), 'r-o',... EbNo, sum_BER(:,3,2), 'g-o', EbNo, sum_BER(:,4,2), 'c-o',... EbNo, sum_BER(:,5,2), 'k-o',... EbNo, ric_ber(:,1,2), 'b-', EbNo, ric_ber(:,2,2), 'r-',... EbNo, ric_ber(:,3,2), 'g-', EbNo,ric_ber(:,4,2), 'c-',... EbNo, ric_ber(:,5,2), 'k-','LineWidth', 1.5) title('Rician model (K = 0.6)') legend('QPSK(simulated)', '8-PSK(simulated)',... '16-QAM(simulated)', '64-QAM(simulated)' ,'256-QAM(simulated)',... 'QPSK(theory)','8-PSK(theory)',... '16-QAM(theory)', '64-QAM(theory)' ,'256-QAM(theory)','location','best') xlabel('EbNo (dB)') ylabel('BER') grid on

يجب أن تحصل على شيء مثل هذا:

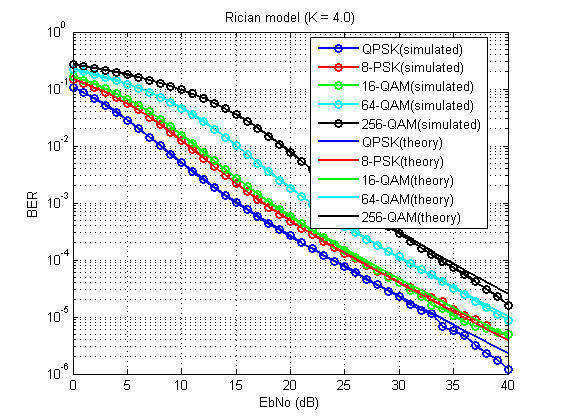
التين. 14. معامل أخطاء البتات للنموذج المدروس (K = 4.0).

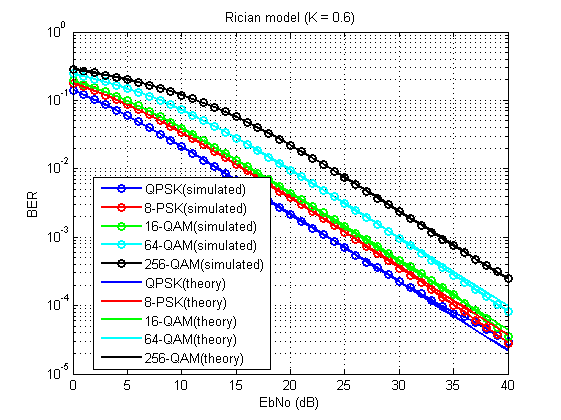
التين. 15. معدل الخطأ في البتات للنموذج المعني (K = 0.6).

ليس بدون عيوب ، بالطبع (بسبب العدد المحدود من المعدلات) ، ولكن بشكل عام ، يمكن أن نرى أنه يعمل!

حسنًا ، ولكن هل سيكون من الممكن توسيع نطاق التجربة إلى حالة MIMO؟ نعم بالطبع.

للقيام بذلك ، نضع افتراضًا واحدًا: تتكون مصفوفة القناة من مسارات انتشار مستقلة ، سيتم توزيع كل منها وفقًا لرايز.

تحت أي ظروف هذا ممكن؟

كما أشرنا أعلاه ، يمكن إنشاء المكون IID في أي بعد. وهذا يعني أن أي قناة MIMO بيضاء مكانية بدون خط البصر يمكن تصميمها على أنها مجموعة من قنوات SISO (حسب بُعد القناة).

مع مكون خط الرؤية أكثر تعقيدًا قليلاً - تحتاج إلى أن تأخذ في الاعتبار موقف حواجز شبكية.

النظر في الصيغة (5): إذا لدينا مصفوفة من خط البصر مكون سيتألف فقط من الوحدات $\ mathbf {H} _ {LoS} = \ mathbf {1}$ ، يبدو أن مكون Raysov يصبح أبيض مكانيًا أيضًا.

لنقترب من هذا ، نكتب خط مكون الرؤية بمزيد من التفصيل أكثر من الصيغة (6):

$\ mathbf {H} _ {LoS} = \ تبدأ {bmatrix} 1 \\ \ exp (j2 \ pi dcos (\ theta_R)) \\. \\. \\. \\ \ exp (j (M_R-1) 2 \ pi dcos (\ theta_R)) \ end {bmatrix} \ start {bmatrix} 1 & \ exp (j2 \ pi dcos (\ theta_T)) &. و. و. & \ exp (j (M_T-1) 2 \ pi dcos (\ theta_T)) \ end {bmatrix}$

ومن المذهل أنه إذا $\ theta_R = \ theta_T = 90 ^ o$ ، ثم ستتألف المصفوفة من وحدة واحدة. هندسيا ، هذا هو الموقف عندما يتم توجيه صفيفين من العناصر بدقة على بعضها البعض:

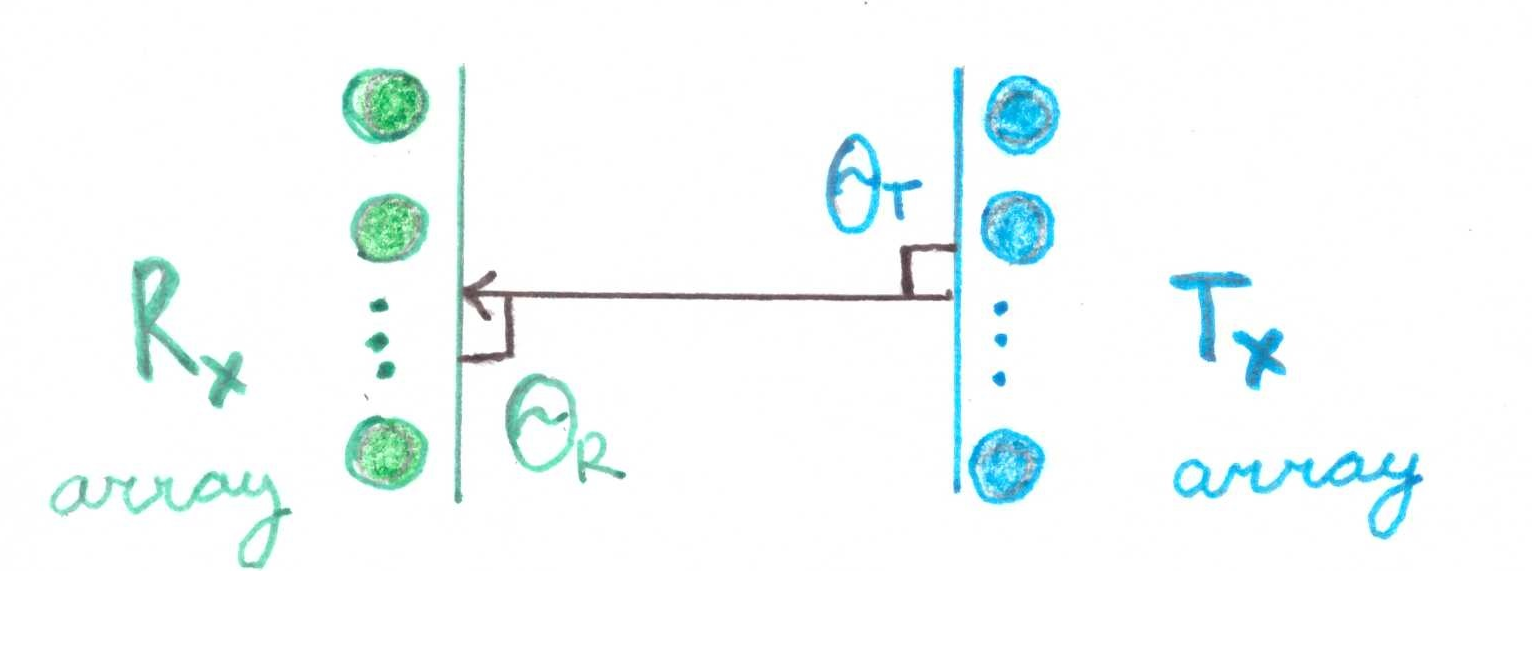
دعونا نفعل مظاهرة الرياضيات قليلا:

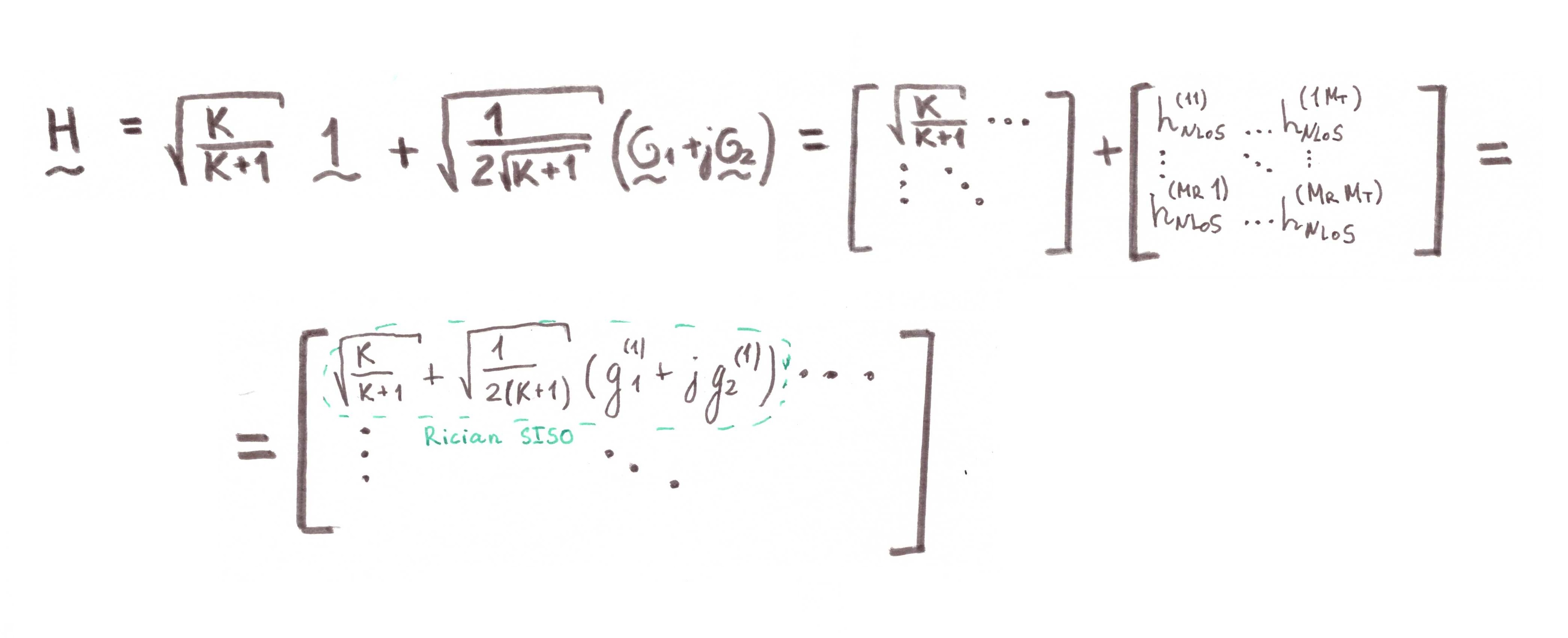
للنمذجة ، نأخذ مخطط Alamouti كأساس. يجب أن تتحول إلى شيء مثل هذا:

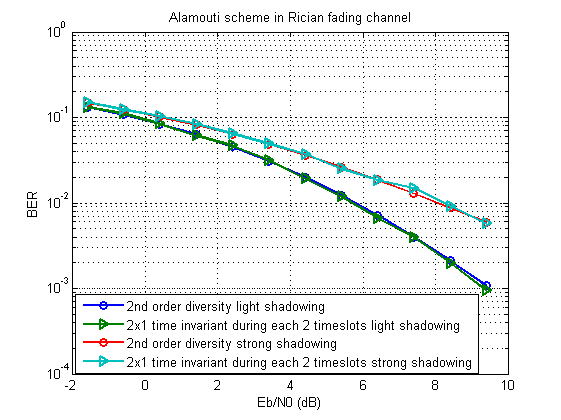
يمكن تنزيل البرنامج النصي الموسع هنا .

أحسنت.

تقريبا أسهل قناة يتلاشى والعلاقة المكانية

والآن ، بعد إكمال رحلتنا إلى عالم الحسابات الإحصائية ، دعنا نقترب قليلاً من الواقع.

أعلاه ، نظرنا في القضية عندما كان مكون عدم وجود خط البصر أبيض مكاني . ومع ذلك ، ينبغي أن يتوقع المرء من الأنظمة الحقيقية بعض الارتباط بين الهوائيات ، وبالتالي بين مسيرات الانتشار لموجة EM.

نقدم متغيرًا جديدًا - مصفوفة الارتباط المكاني:

$\ mathbf {R} = E \ {vec (\ mathbf {H}) vec (\ mathbf {H}) ^ H \} \ qquad (8)$

حيث يشير vec إلى عملية vectorization . بالمناسبة ، سوف تؤثر هذه المصفوفة فقط على عنصر عدم وجود خط البصر ، وبالتالي في هذه الحالة $\ mathbf {H} = \ mathbf {H} _ {NLoS}$ .

مثال على MIMO 2x2

من المنطقي أن نفترض أنه في الحياة الواقعية ، يتم تحديد هذه المصفوفة أولاً من خلال القياسات ، وعندها فقط يتم استخدامها للنمذجة:

$vec (\ mathbf {H} _ {NLoS}) = \ mathbf {R} ^ {1/2} vec (\ mathbf {H} _w) \ qquad (9)$

حيث $\ mathbf {H} _w$ هي مصفوفة IID (يعني w المكاني w hite).

لاحظ أن رفع مصفوفة إلى قوة ليس زيادة في قوة كل عنصر من عناصرها. لذلك ، في حالتنا ، لا يمكن استخدام الدالة sqrt () في MatLab . استخدم المشغل ^ .
في حالة Python ، لا يمكنك استخدام عامل الأس ، ** وطريقة sqrt الخاصة بالوحدة الرديئة الشائعة. تحتاج إلى استخدام طريقة fractional_matrix_power لوحدة scipy .

إذا كان المستقبِل والمُرسِل مستقلان بما فيه الكفاية عن بعضهما البعض ، كما في الشكل 16 ، يمكن عندئذٍ تطبيق نموذج Kronecker [1 ، ص. 40] ، لتقليل عدد المعاملات لحساب:

$\ mathbf {R} = \ mathbf {R} ^ T_T \ otimes \ mathbf {R} _R \ qquad (10)$

حيث $\ otimes$ يدل على عمل Kronecker .

ليوبولد كرونيكر

نحن نفكر بشكل منفصل في مكونات مصفوفة التعبير:

$\ mathbf {R} _R = \ frac {1} {M_T} E \ left \ {\ left (\ mathbf {H} _ {NLoS} \ mathbf {H} ^ H_ {NLoS} \ right) ^ T \ right \ }$ هي مصفوفة الارتباط للهوائيات المستقبلة ،

$\ mathbf {R} _T = \ frac {1} {M_R} E \ left \ {\ mathbf {H} ^ H_ {NLoS} \ mathbf {H} _ {NLoS} \ right \}$ هي مصفوفة الارتباط لنقل الهوائيات

$M_R$ و $M_T$ - هذا هو عدد هوائيات الاستقبال والإرسال ، على التوالي. كلا المصفوفات مصفوفة هيرمتية شبه محددة. علاوة على ذلك ، رتبة المصفوفة $\ mathbf {H} _ {NLoS}$ محدودة من حيث القيمة $min (المرتبة (\ mathbf {R} _T) ، الترتيب (\ mathbf {R} _R))$ .

التين. 16.
نموذج ناشرون في حالة المستقبِل والمُرسِل غير المرتبط. النقاط الخضراء تعني الناشرون ، يعني المستلم والارسال الأزرق والأحمر. أعتذر عن الجودة ، فهذه لقطة شاشة لأحد واجبات TU Ilmenau.

يمكن كتابة مصفوفة القناة في هذه الحالة على النحو التالي:

$\ mathbf {H} = \ sqrt {\ frac {K} {K + 1}} \ mathbf {H} _ {LoS} + \ sqrt {\ frac {1} {K + 1}} \ mathbf {R} ^ {1/2} _R \ mathbf {H} _ {w} \ left (\ mathbf {R} ^ {1/2} _T \ right) ^ H \ qquad (11)$

ومع ذلك ، في حالات مثل ، على سبيل المثال ، في الشكل 17 ، لا يزال يتعين عليك استخدام مصفوفة الارتباط الكامل (انظر الصيغة (9)).

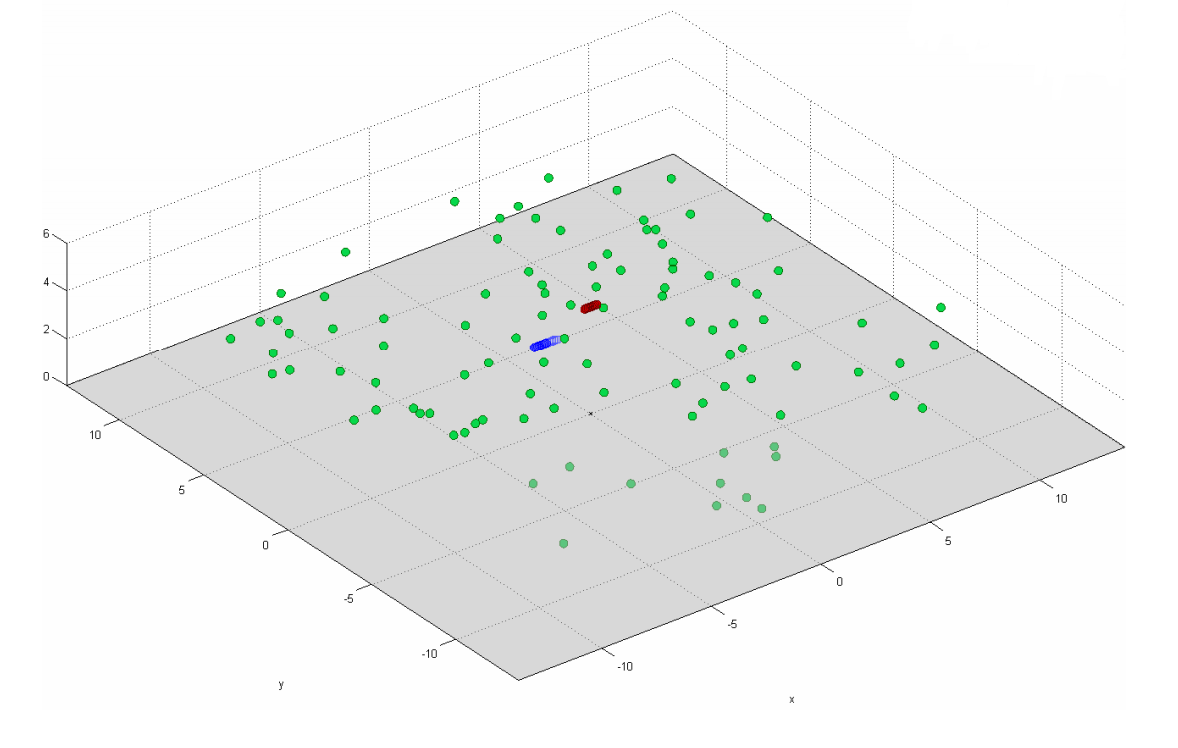
التين. 17. نموذج من الناشرون في حالة ربط المتلقي والارسال. النقاط الخضراء تعني الناشرون ، يعني المستلم والارسال الأزرق والأحمر.

لتوحيد ما تعلمناه ومعرفة مدى تعقيد الارتباط المكاني للحياة ، فلنحاول حساب عرض النطاق الترددي للقنوات. على سبيل المثال ، ل MIMO 2x2.

للقيام بذلك ، نأخذ الحالات التالية (نعني نفس الخبو المسطح ، للبساطة ، نحن أيضًا نعتبر قناة رايلي فقط):

1) قناة بيضاء مكانيا ؛
2) نموذج Kronecker مع وجود علاقة ضعيفة نسبيا:

$\ mathbf {R} _T = \ mathbf {R} _R = \ تبدأ {bmatrix} 1 & 0.4 \\ 0.4 & 1 \ end {bmatrix}$

3) نموذج Kronecker مع وجود علاقة قوية نسبيا:

$\ mathbf {R} _T = \ mathbf {R} _R = \ تبدأ {bmatrix} 1 & 0.6 \\ 0.6 & 1 \ end {bmatrix}$

سوف نستخدم بيثون 3.4 في هذا الجزء. سيتم احتساب وظيفة حساب النطاق الترددي من أحد مطبوعاتي السابقة .

 import numpy as np from numpy import linalg as LA import matplotlib.pyplot as plt from scipy.linalg import fractional_matrix_power def openloop_capacity(H_chan, SNR_dB): SNR = 10**(SNR_dB/10) Mt = np.shape(H_chan)[1] H_sq = np.dot(H_chan,np.matrix(H_chan, dtype=complex).H) lambdas = LA.eigvals(H_sq) lambdas = np.sort(lambdas)[::-1] c = 0 for eig in lambdas: c = c + np.log2(1 + SNR*eig/Mt) return np.real(c)

تحديد المعالم الرئيسية للنظام:

 Mr = 2 # number of receive antennas Mt = 2 # number of transmit antennas Rr1 = np.array([[1., .4], [.4, 1.]]) # case 1 Rr2 = np.array([[1., .6], [.6, 1.]]) # case 2 Rt1 = np.array([[1., .4], [.4, 1.]]) # case 1 Rt2 = np.array([[1., .6], [.6, 1.]]) # case 2 Rr1_half = fractional_matrix_power(Rr1, 0.5) Rr2_half = fractional_matrix_power(Rr2, 0.5) Rt1_half = fractional_matrix_power(Rt1, 0.5) Rt1_half_H = np.conj(Rt1_half).T Rt2_half = fractional_matrix_power(Rt2, 0.5) Rt2_half_H = np.conj(Rt2_half).T

نبدأ المحاكاة:

 counter = 1000 SNR_dBs = [i for i in range(1, 21)] C_MIMO_uncorr = np.empty((len(SNR_dBs), counter)) C_MIMO_kron1 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron2 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron3 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron4 = np.empty((len(SNR_dBs), counter)) for c in range(counter): H_uncorr = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2) H_kron1 = np.dot(Rr1_half, np.dot(H_uncorr, Rt1_half_H)) H_kron2 = np.dot(Rr2_half, np.dot(H_uncorr, Rt2_half_H)) for idx, SNR_dB in enumerate(SNR_dBs): C_MIMO_uncorr[idx, c] = openloop_capacity(H_uncorr, SNR_dB) C_MIMO_kron1[idx, c] = openloop_capacity(H_kron1, SNR_dB) C_MIMO_kron2[idx, c] = openloop_capacity(H_kron2, SNR_dB) C_MIMO_uncorr_erg = np.mean(C_MIMO_uncorr, axis=1) C_MIMO_kron1_erg = np.mean(C_MIMO_kron1, axis=1) C_MIMO_kron2_erg = np.mean(C_MIMO_kron2, axis=1)

رسم

 plt.figure(figsize=(7, 5), dpi=100) plt.plot(SNR_dBs, C_MIMO_uncorr_erg,'g-o', label='Uncorrelated') plt.plot(SNR_dBs, C_MIMO_kron1_erg, 'm-o', label='Kronecker model, case 1') plt.plot(SNR_dBs, C_MIMO_kron2_erg, 'r-o', label='Kronecker model, case 2') plt.title("Rayleigh flat fading (MIMO 2x2)") plt.xlabel('SNR (dB)') plt.ylabel('Ergodic capacity (bps/Hz)') plt.legend() plt.minorticks_on() plt.grid(which='major') plt.grid(which='minor', linestyle=':') plt.show()

نحصل على:

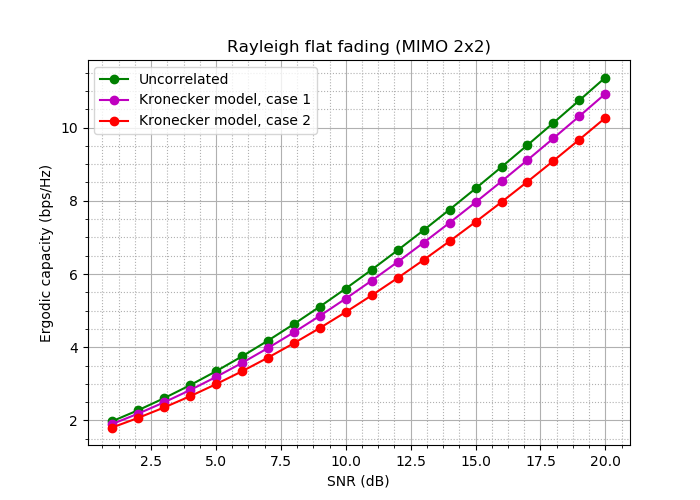
التين. 18. منحنيات عرض النطاق الترددي لهذه التجارب.

حسنًا: الفرق ، رغم أنه غير حاسم ، هو!

خاتمة

ربما يلاحظ أحد القراء أن كل شيء تقريبًا فحصناه اليوم (بالتفصيل وبشكل عابر) يعتمد جيدًا على معلمات كائن matlab comm.MIMOChannel . هذه الحقيقة تبدو لي مهمة للغاية:

أولا ، أنه ينظم ما ورد أعلاه ،
وثانيا ، إنه يؤكد أننا نعالج القضايا الحالية.

حسنًا ، والآن ، إذا كنت تستخدم هذه الكتل ، فأرجو أن يكون الأمر أكثر وضوحًا لماذا وما هي الأقلام التي تحتاج إلى تحريفها.

شكرا لكم جميعا على اهتمامكم!

سأضيف هنا رابطًا إلى الشرائح حول هذا الموضوع من راينر س. ثوما ( الميناو ) ، الذي ألقى علينا محاضرات في ذلك الوقت. أعتقد أن شخصا ما سوف يكون في متناول اليدين!

أدب

بولراج ، أروجواسوامي ، روهيت نبار ، ودانانجاي غور. مقدمة في الاتصالات اللاسلكية الزمكان. مطبعة جامعة كامبريدج ، 2003.
جولدسميث أ. الاتصالات اللاسلكية. - مطبعة جامعة كامبريدج ، 2005.
Fontæn ، فرناندو بيريز ، و Perfecto Mariæo Espiæeira. نمذجة قناة الانتشار اللاسلكية: نهج محاكاة مع Matlab. المجلد. 5. جون ويلي وأولاده ، 2008.
فاروخي ، فاروق ر. وآخرون. "الكفاءة الطيفية للأنظمة اللاسلكية FDMA / TDMA مع صفيفات هوائي الإرسال والاستقبال." معاملات IEEE على الاتصالات اللاسلكية 1.4 (2002): 591-599.

أسهل قناة MIMO تقريبًا مع تلاشي (نموذج Kronecker متضمن)