فركتلات بأعداد غير عقلانية. الجزء 2

الجزء 0: فركتلات في الأعداد الأولية.
الجزء 1: فركتلات في أرقام غير عقلانية.



تحتوي المقالة على صور GIF وصور متناقضة. قد يكون الصرع نوبة صرع.

في مقال سابق ، نظرنا في خوارزمية تصور تسلسل ثنائي. لنتذكر.

خذ التسلسل الثنائي. على سبيل المثال ، البتات القليلة الأولى من التسلسل الكسري نوقشت في مقال سابق:

$$

$$Q_n = \ lfloor n \ sqrt {2} \ rfloor \؛ (\ textrm {mod} \؛ 2) ؛ \ quad n = 0،1،2 ، ...$$

0100110110010011001001101100

نرسم حقل خلية مربعة. وضعنا البتات في الحدود العليا. المسافة بين البتات هي خليتان:



لكل بت ، ارسم مسارًا متقطعًا على طول المائل (عبر الخلية). بالنسبة للأصفار ، ارسم الحد الأول على اليمين:



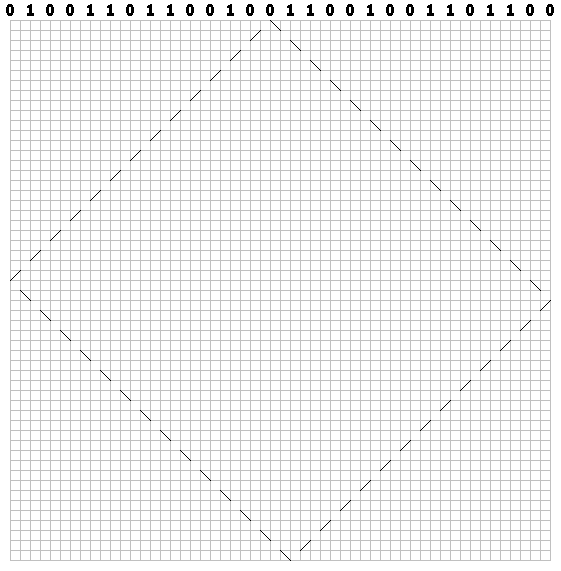
للوحدات - إلى اليسار:



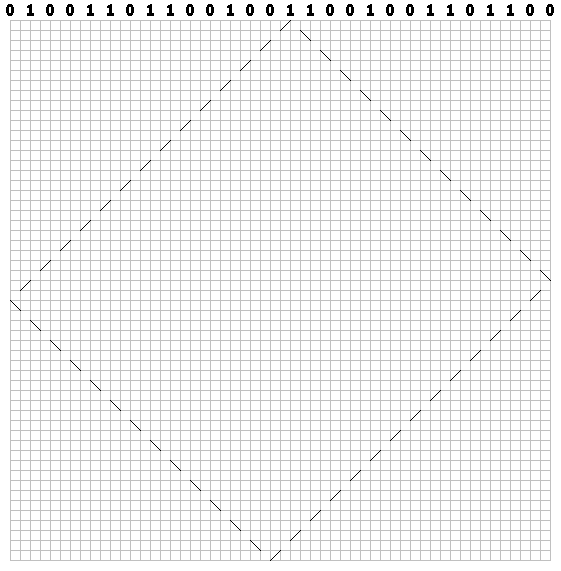
ارسم مسار لكل بت. لدينا نمط "البلياردو":



يمكن الحصول على نمط مماثل (بدون عيب قطري - التسلسل لانهائي ، تصورنا أنه تسلسل نهائي) بطريقة أخرى. اقلب كل زوج بت في التسلسل:

0 - 0 1 1 - - - 1 1 - - 0 1 1 - - 1 1 1 - - 1 1 1 - - 1

بعد ذلك ، ارسم خطوط متقطعة رأسية لكل قطعة:



وضعنا البتات على اليسار ، ورسم خطوط أفقية:



نحن نجمع بين:



بعد كتابة المقال الأول ، بقي سؤالان دون حل:

1. هل من الممكن رسم نمط كسورية للأرقام غير عقلانية. يمكنك ذلك. تم حل المشكلة في مقال سابق. في الصورة أعلاه - جزء من نمط كسورية ل $$$\ sqrt {2}$. إذا قمت بتحديد أحد المنحنيات في هذا النمط:



الحصول على منحنى كسورية المعروفة - "كلمة فيبوناتشي كسورية".

2. السؤال الثاني هو ما إذا كان من الممكن كتابة خوارزمية ترسم نمطًا:



سيتم تناول العدد الثاني في هذه المقالة. سنقوم بتلوين الأنماط بمساعدة النول الذي نحاكي عمله باستخدام JavaScript.



في الرسم البياني أعلاه - أسهل آلة. يتكون من إطارين يتم من خلالهما تمديد الخيوط. ترتبط الأطر الدواسات. عندما تضغط على إحدى الدواسات ، يرتفع أحد الإطارات. الخيوط المرسومة من خلال هذا الإطار ترتفع ويمتد مؤشر ترابط عرضي في الفجوة الناتجة بين المواضيع. إذا قمت بتمديد الخيوط المتساوية والغريبة عبر إطارات مختلفة ، فستحصل على نسج في نمط رقعة الشطرنج:



في الأجهزة الأكثر تعقيدًا ، يتم استخدام أربعة إطارات أو أكثر:


آشفورد 4 رمح الجدول المنوال

من أجل عدم الخلط بينه وبين دواسة للضغط ، فإنها رسم تخطيطي.



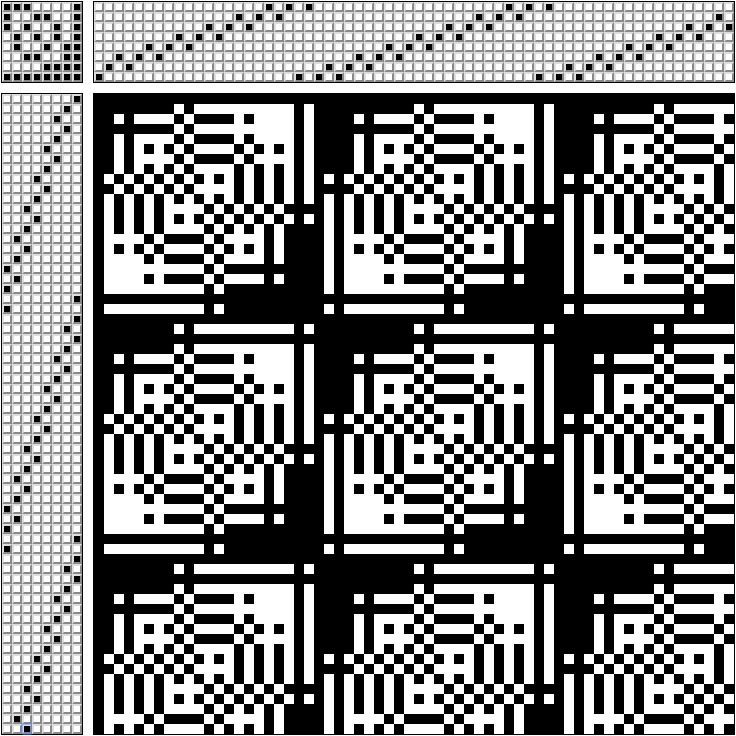
يشار في الجزء العلوي الأيمن من النموذج إلى أي إطارات تذهب الخيوط (نمط للنوم ذي 8 إطارات)

في الزاوية العلوية اليسرى - والتي يتم تثبيت الدواسات في نفس الوقت (كل دواسة متصلة فقط بإطارها الخاص).

في الجزء السفلي الأيسر - في ما أجل دواسة.

في الجزء السفلي الأيمن - ما نسج نحصل عليه. إذا قمت بتمديد الخيط الأبيض من خلال الأسود - نحصل على نمط أحادي اللون.

"الدخول" على الفور قد يبدو المبدأ صعبًا بعض الشيء. الصورة أدناه توضح كيف يتم تشكيل نمط النسيج:



دعنا نكتب السيناريو. سنقوم بتمديد الخيوط خلال الإطارات باستخدام الصفيف أحادي البعد صفيف 2. في صفيف صفيف أحادي البعد 1 ، نكتب تسلسل لقط الدواسة. في array3 (صفيف ثنائي 8 × 8) نكتب أي دواسات يجب تثبيتها في نفس الوقت.

for(var i=0;i<length;i++){ for(var j=0;j<length;j++){ if(array3[array1[i]][array2[j]]){ context.fillRect(i, j, 1, 1); } } } 

النصي (يعمل في جوجل كروم).

مع مساعدة تلوح في الأفق لدينا ، يمكننا رسم مجموعة واسعة من الأنماط:



لكن ذلك تاريخيا ، الشخص العادي ليس لديه أكثر من قدمين. لذلك ، من الملائم تثبيت أكثر من دواسين في وقت واحد. أحد النماذج الأكثر شيوعًا للنول على النحو التالي:



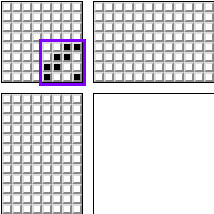
لمدة 4 إطارات. وتعديله لمدة 8 إطارات:



بشكل غير متوقع ، تشبه الأنماط (أو جزء من الأنماط) التي تم إنشاؤها باستخدام هذا القالب أنماط "البلياردو" الخاصة بنا. بالإضافة إلى ذلك ، هذه الأنماط مظللة:



يمكنك تعلم اختيار أنماط "البلياردو" للنول. مثال:



في بداية المقال ، رأينا بالفعل جزءًا من هذا النمط.

مع الانتهاء من تلوح في الأفق وكتابة برنامج نصي لتصور تسلسل ثنائي. يمكننا التخلص من واحدة من المصفوفات - النمط متماثل قطري. كيفية ملء مجموعة المتبقية؟ الابتدائية:



نحن نأخذ التسلسل ل $$$\ sqrt {2}$. إنشاء مجموعة. في عنصر صفر من الصفيف ، اكتب بت صفر من التسلسل. بالتناوب تأخذ كل بت من التسلسل. إذا كانت بت nth = 1 - اكتب إلى الصفيف a [n] = a [n-1] +1. إذا كانت bit = 0 - اكتب [n] = a [n-1] -1

$$

$$Q_n = \ lfloor n \ sqrt {x} \ rfloor \؛ (\ textrm {mod} \؛ 2) ؛ \ quad n = 0،1،2 ، ... \\ a_n = \ start {cases} a_ {n-1} +1 ، Q_n = 1 ؛ \\ a_ {n-1} -1 ، Q_n = 0 \ end { الحالات}$$

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } 

نتحقق من:

  for(var i=0;i<size;i++){ context.fillRect(i, a[i]+50, 1, 1); } 

في الواقع ، لقد تلقينا بالفعل كسورية الابتدائية ، ولكن سنستمر.

بعد ذلك ، سنتعامل مع المصفوفة:



لخص $$$x$و $$$ذ$. قسّم المعامل على 4. إذا كانت النتيجة الناتجة = 0 أو 1 - اكتب المصفوفة بشكل صحيح. لمدة 2 و 3 ، اكتب خطأ. يمكننا الاستغناء عن مصفوفة (من غير المعروف مسبقًا ما هي القيم القصوى والدنيا التي يأخذها [n]). تلخيص [x] و [y]. إلى المبلغ الناتج ، أضف بعض الأرقام $$$C$(للتخلص من تلك الحالات عندما يكون المبلغ عددًا سالبًا). قسّم المعامل على 4. للقيم 0 و 1 ، قم بالطلاء على البيكسل بالإحداثيات $$$x$و $$$ذ$.

تأخذ الخوارزمية النهائية بضعة أسطر فقط:

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } for(var x=0;x<size;x++){ for(var y=0;y<size;y++){ q=(a[x]+a[y]+512)%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); } } 

تصور تسلسل كسورية لدينا.

$$

$$Q_n = \ lfloor n \ sqrt {2} \ rfloor \؛ (\ textrm {mod} \؛ 2) ؛ \ quad n = 0،1،2 ، ...$$

يمكنك بسهولة تعديل البرنامج النصي للحصول على صورة RGB:

  q=(a[x]+a[y]+512)%4; /*if(q==0 || q==1) context.fillRect(x, y, 1, 1);*/ if(q==0) context.fillStyle = 'rgb(255,0,0)'; if(q==1) context.fillStyle = 'rgb(0,255,0)'; if(q==2) context.fillStyle = 'rgb(0,0,255)'; if(q==3) context.fillStyle = 'rgb(0,0,0)'; context.fillRect(x, y, 1, 1); 

أعلاه ، أضفنا رقماً إلى مجموع a [x] + a [y] $$$C$. إذا لم تقم بإضافة هذا الرقم ، فإن الحد الأدنى لقيمة المبلغ = -8 ، والحد الأقصى = 8 (لـ $$$x$و $$$ذ$من 0 إلى 750). إذا قمت بإزالة $$$C$- في بعض الحالات ، يتبين أن المجموع سالب وليس مضاعفًا للرابع ، وفي هذه الحالات لا يتم رسم البيكسل (يبقى أسود):

  q=(a[x]+a[y])%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); 

يمكنك أن تتخيلها كما لو أن جزءًا من الفراكتل يقع أسفل بعض الحدود الوهمية (أسفل هذا الحد ، القيم السلبية فقط هي مضاعفات 4: -4 ، -8 ، -12 ، ...).

يمكننا أن نرى أين تقع هذه الحدود:

  if(a[x]+a[y]>=0) context.fillRect(x, y, 1, 1); 

بدلاً من تقسيم المعامل ، يمكننا مقارنة المجموع بقيمة محددة معينة ، وبالتالي الطلاء على "طبقة" واحدة فقط من الفركتلات. كمثال ، خذ المتوسط ​​بين الحد الأدنى والحد الأقصى للقيم:

  q=(a[x]+a[y]); if(q==0) context.fillRect(x, y, 1, 1); 

تغيير القيم من الحد الأدنى إلى الحد الأقصى ، يمكننا أن نرى كيف تتغير "الطبقات" في الديناميات:




بالإضافة إلى ذلك ، يمكننا "على الجبهة" مقارنة [x] بـ [y] وأيضًا الحصول على نمط كسري:

 if(a[x]==a[y]) context.fillRect(x, y, 1, 1); 

التسلسل التالي:

$$

$$Q_n = \ lfloor n (\ sqrt {2} +1) \ rfloor \؛ (\ textrm {mod} \؛ 2) ؛ \ quad n = 0،1،2 ، ...$$

كسورية:



RGB:



الطبقة الوسطى:



في الديناميات:

$$

$$Q_n = \ lfloor n \ sqrt {3} \ rfloor \؛ (\ textrm {mod} \؛ 2) ؛ \ quad n = 0،1،2 ، ...$$

كسورية:



RGB:



الطبقة الوسطى:



في الديناميات:

$$

$$Q_n = \ lfloor n (\ sqrt {3} +1) \ rfloor \؛ (\ textrm {mod} \؛ 2) ؛ \ quad n = 0،1،2 ، ...$$

كسورية:



RGB:



الطبقة الوسطى:



في الديناميات:

$$

$$Q_n = \ lfloor n \ sqrt {5} \ rfloor \؛ (\ textrm {mod} \؛ 2) ؛ \ quad n = 0،1،2 ، ...$$

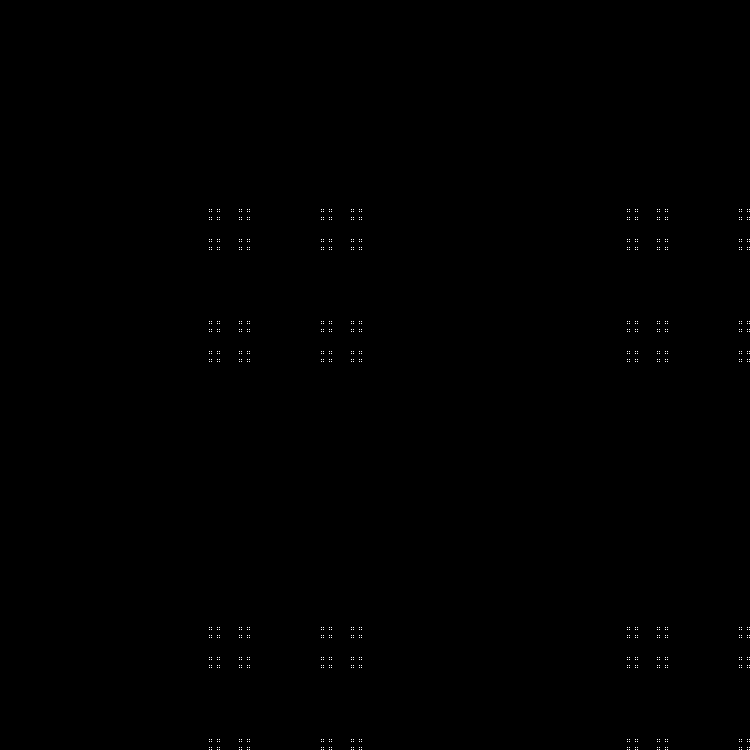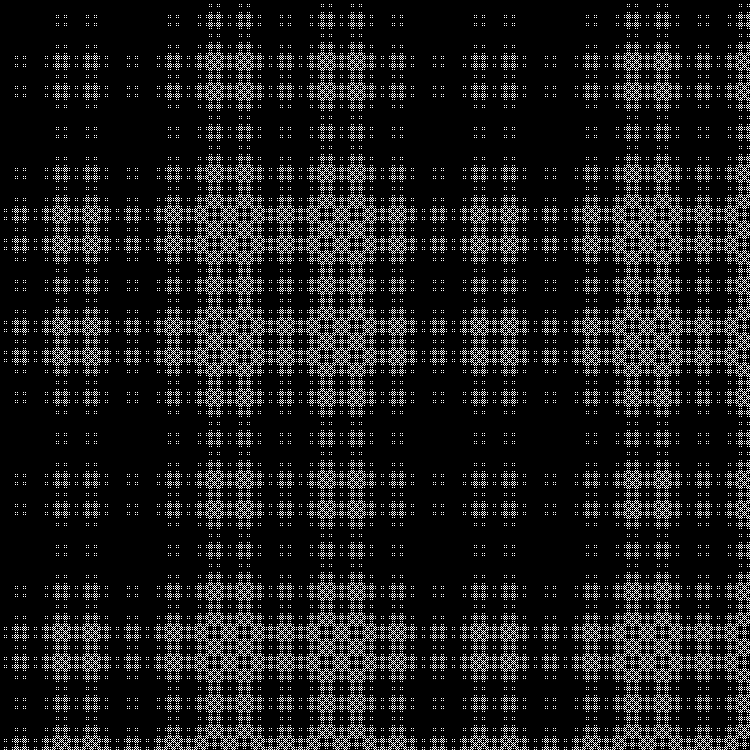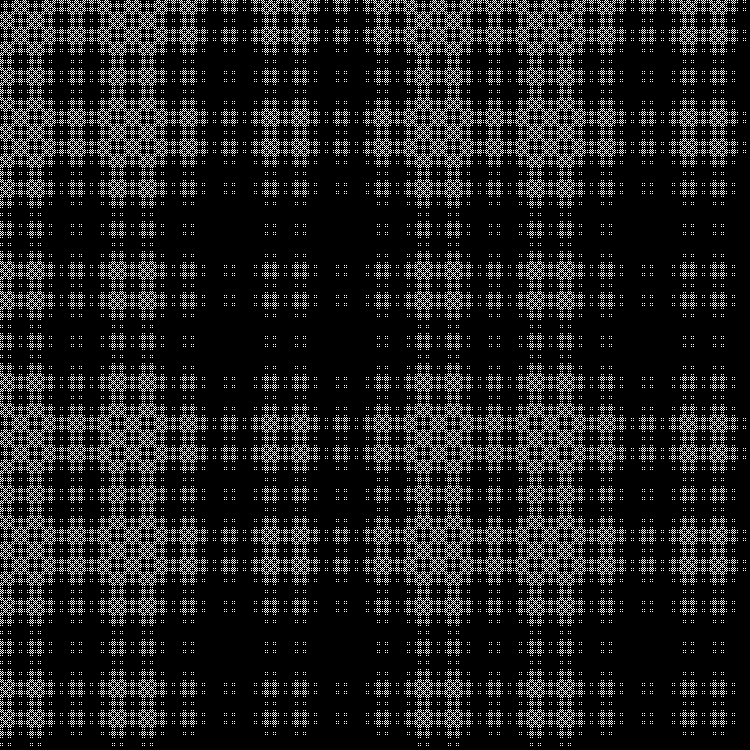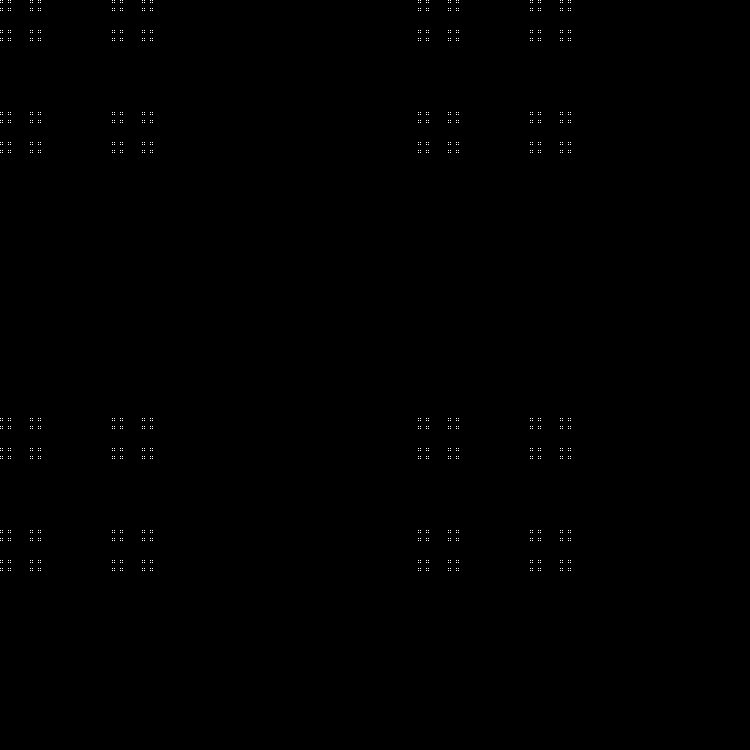
كسورية:



RGB:



الطبقة الوسطى:



في الديناميات:



حسنًا ، لدينا كسورية مفضلة (يمكن رسم جزء من هذا النموذج باستخدام البلياردو ، بأحجام جانبية تساوي أرقام فيبوناتشي):

$$

$$Q_n = \ lfloor n (\ sqrt {5} +1) \ rfloor \؛ (\ textrm {mod} \؛ 2) ؛ \ quad n = 0،1،2 ، ...$$

كسورية:



RGB:



الطبقة الوسطى:



في الديناميات:



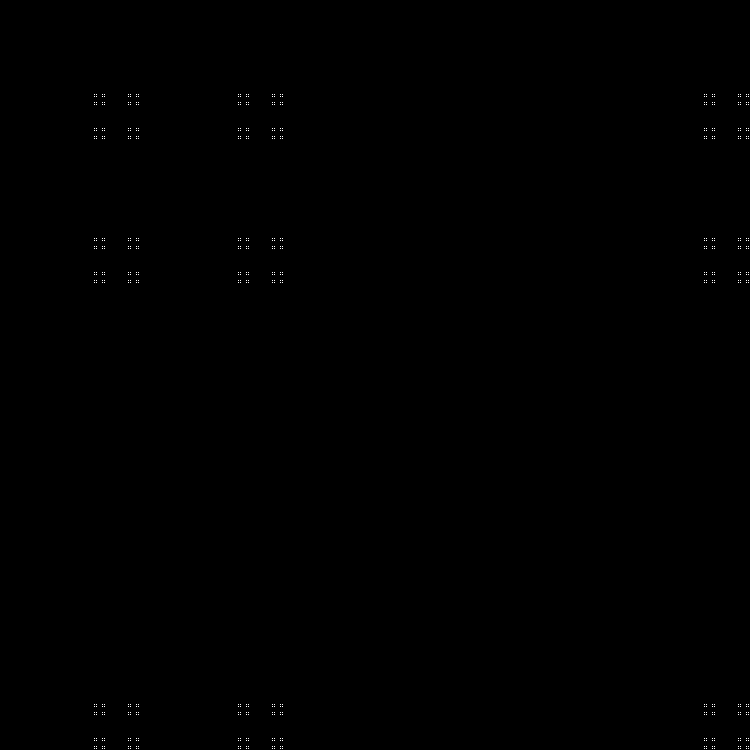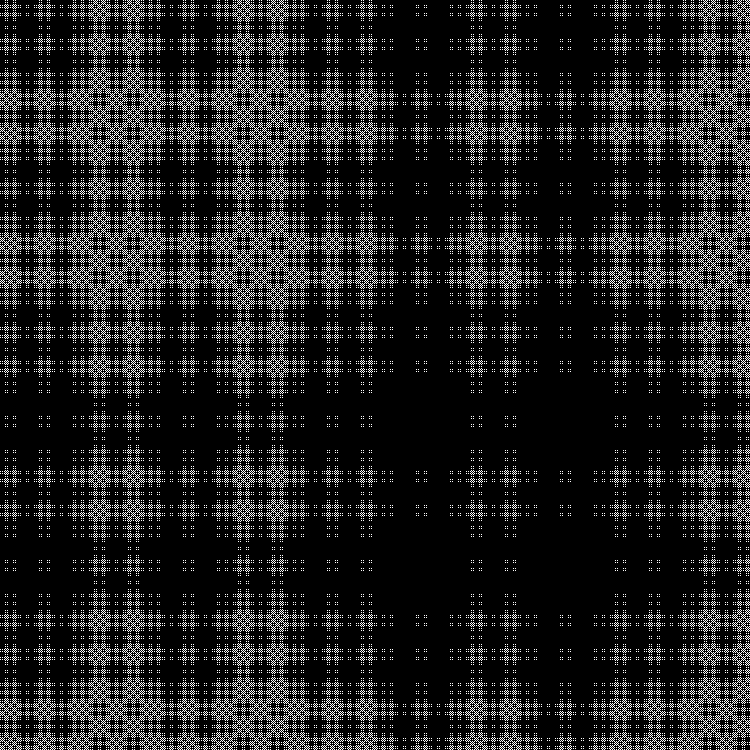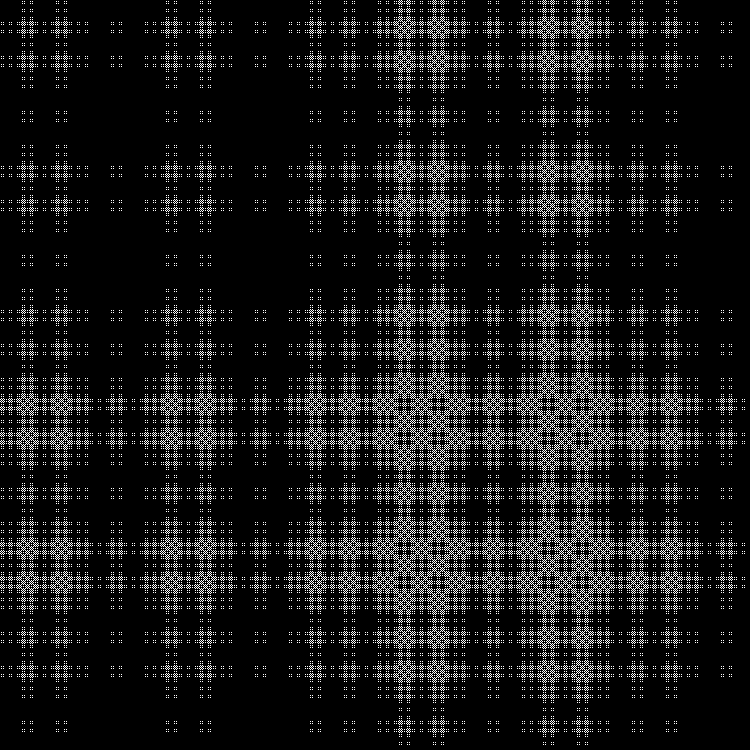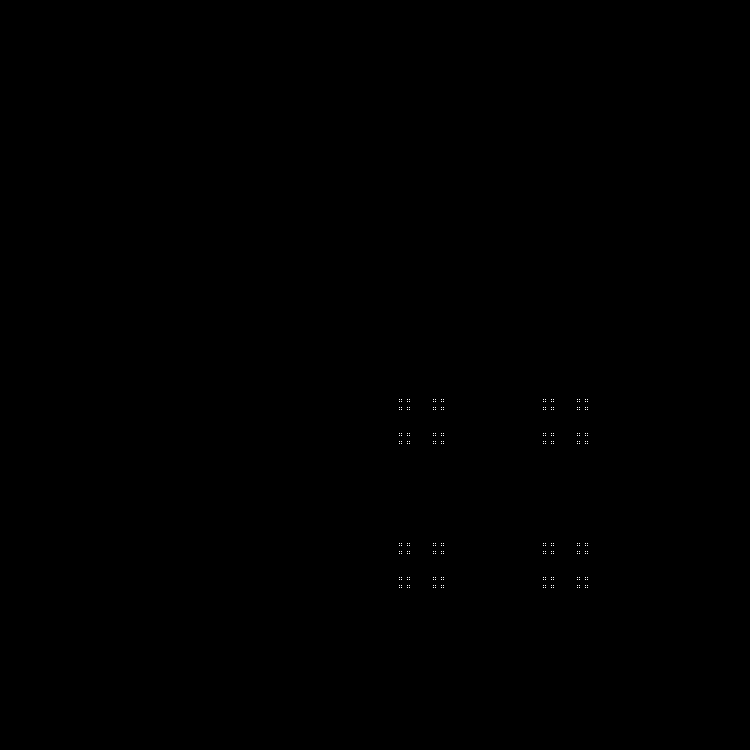
تسلسل آخر لإكماله:

$$

$$Q_n = \ lfloor n ^ {2} \ sqrt {2} \ rfloor \؛ (\ textrm {mod} \؛ 2) ؛ \ quad n = 0،1،2 ، ...$$

نمط:



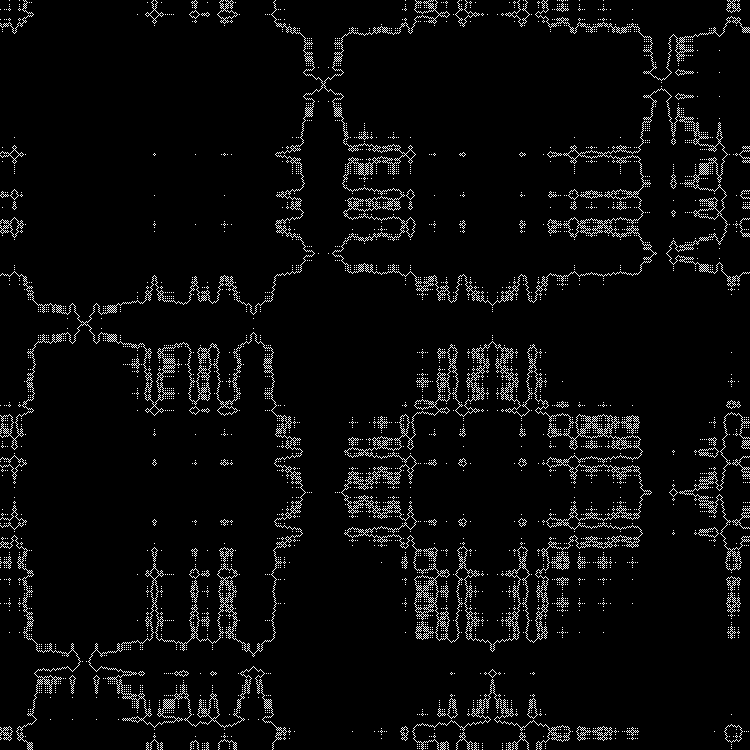
RGB:



الطبقة الوسطى:



في الديناميات:



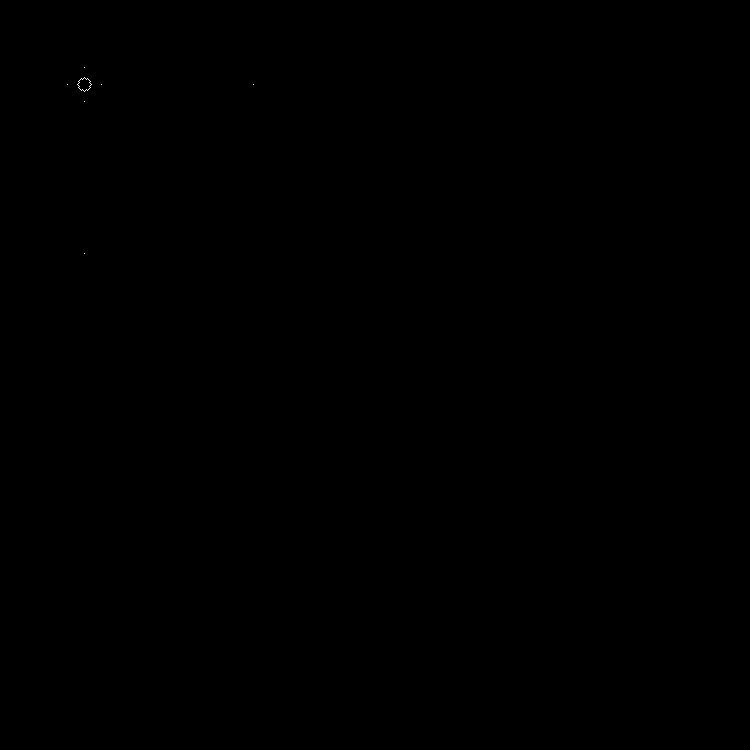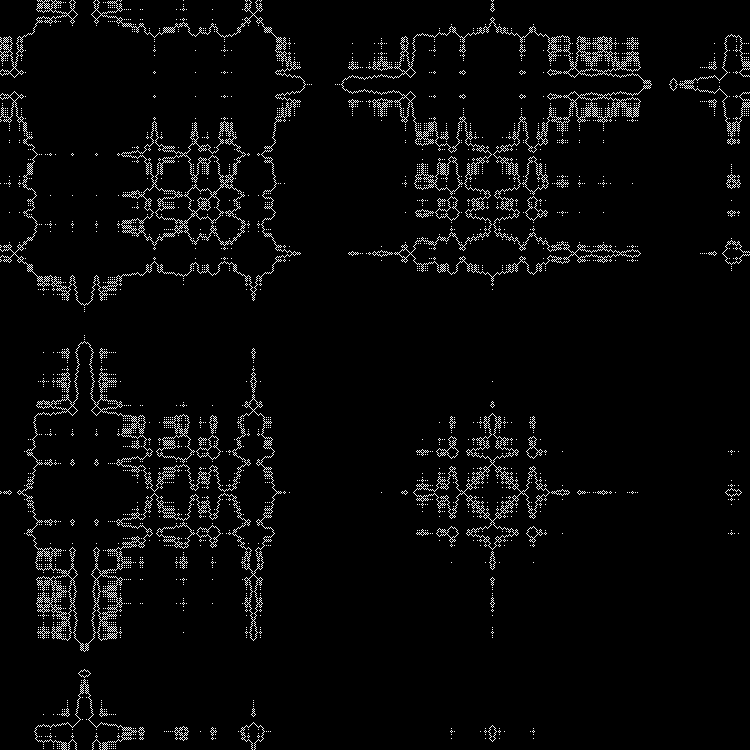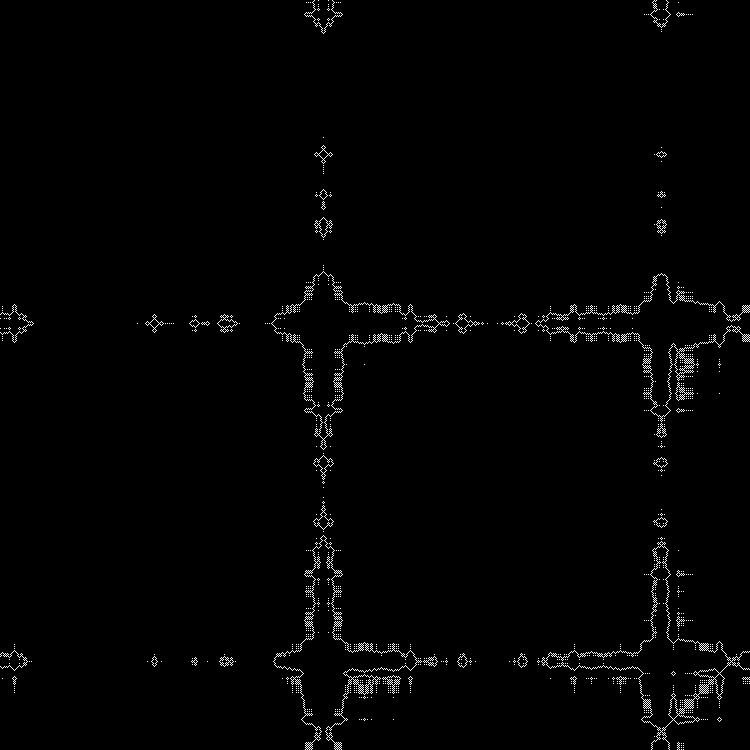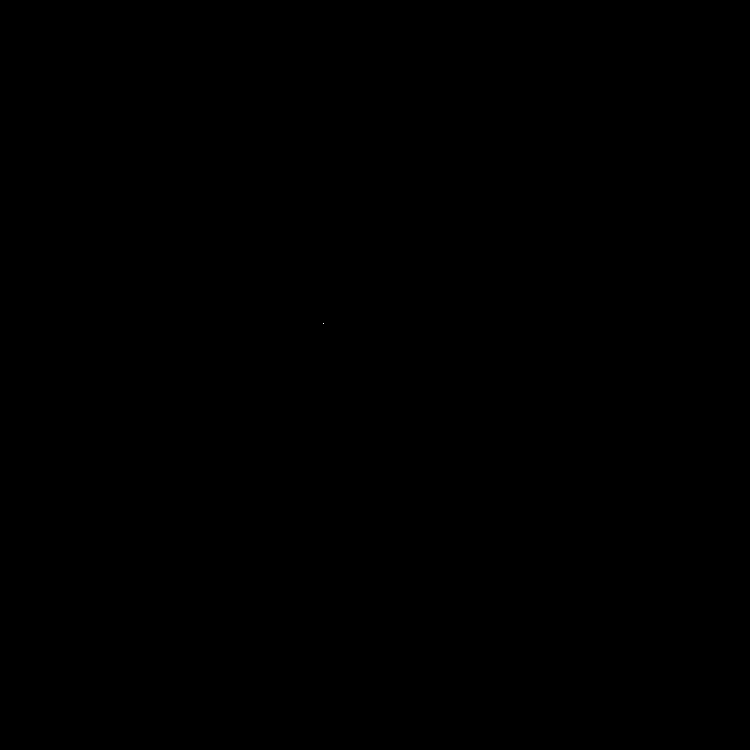
يمكن أن تكون مدفوعة جذور مربعة أخرى في البرنامج النصي . (يمكنك أن تقود سيارتك بقيم كسرية).

في البرنامج النصي الثاني ، يمكنك قيادة التسلسل يدويًا.

سيناريو آخر للبلياردو. إحداثيات الماوس - أبعاد البلياردو. يتكون النموذج الموجود على اليسار من التسلسل الذي تم الحصول عليه باستخدام باقي القسمة (التفاصيل في المقال السابق). على الجانب الأيمن - التكافؤ $$$\ lfloor n \ frac {y} {x} \ rfloor$.