تقدير VaR و ConVaR لسعر سهم الشركة الكازاخستانية

خلال العقود الماضية ، يقع الاقتصاد العالمي بانتظام في دوامة الأزمات المالية التي أثرت على كل بلد. لقد أدى ذلك تقريبًا إلى انهيار النظام المالي الحالي ، نظرًا لهذه الحقيقة ، أصبح جميع الخبراء في النمذجة الرياضية والاقتصادية يستخدمون أساليب للسيطرة على خسائر الأصول والمحفظة في العالم المالي (Lechner، LA، and Ovaert، TC) (2010): هناك اتجاه متزايد نحو النمذجة الرياضية للعملية الاقتصادية للتنبؤ بسلوك السوق وتقييم استدامتها (المرجع نفسه) ، فبدون الاهتمام اللازم للسيطرة على التهديدات وتقييمها بشكل صحيح ، يفهم الجميع أنها قادرة على إطلاق تكلفة هائلة في تطوير المنظمة أو حتى إفلاسها.

لقد كانت القيمة المعرضة للمخاطر (VaR) في نهاية المطاف نهجًا منتظمًا لجذب المخاطر بين المؤسسات في القطاع المالي والجهة المنظمة لها (Engle، R.، and Manganelli S.، 2004). يتم تطبيق النموذج في الأصل لتقدير قيمة الخسارة في محفظة الاستثمار خلال فترة زمنية محددة وكذلك في احتمال حدوث معين. إلى جانب حقيقة استخدام VaR في القطاع المالي ، هناك الكثير من الأمثلة لتقييم القيمة المعرضة للخطر في مجالات مختلفة مثل توقع الطاقم الطبي لتطوير إدارة موارد الرعاية الصحية Zinouri، N. (2016). على الرغم من بدائيته التطبيقية في تجربة حقيقية ، فإن النموذج يتكون من عيوب في التقييم ، (المرجع نفسه).

الهدف من التقرير هو وصف لنموذج VaR الحالي بما في ذلك أحد إصدارات الترقية الخاصة به ، وهي القيمة الشرطية للخطر (CVaR). في القسم التالي والقسم 3 ، يتم شرح خوارزمية التقييم واختبار النموذج. للحصول على توضيح واضح ، يتم تقدير الخسارة المتوقعة على أصل إحدى الشركات الكازاخستانية المتداولة في سوق الأوراق المالية في فترة زمنية طويلة. يناقش القسمان الأخيران 4 و 5 ويظهران نتائج العمل البحثي.

خلفية

يُعتقد أن الاستخدام الأول لـ VaR من قبل المؤسسات المالية العملاقة قبل 40 عامًا ونتيجة لذلك أصبحت VaR شائعة بين الشركات التجارية الأخرى ، حتى أن المنظمين الماليين قد اهتموا بالنموذج (Linsmeier، TJ، Pearson، ND 2000). على سبيل المثال ، أدرجت لجنة الأوراق المالية والبورصات الأمريكية VaR في قائمة الطرق الكمية لحساب مخاطر السوق والممتلكات في عام 1997 (المرجع نفسه).

في الواقع ، وفقًا لمقالات Lechner و LA و Ovaert ، TC (2010) وكذلك Linsmeier و TJ و Pearson ، ND (2000) ، تعد VaR معادلة تقدير معبّر عنها في الوحدات النقدية ولا تتجاوز الخسارة في نطاق المقدار خلال فترة زمنية معينة ومستوى ثقة معين. عادةً ما يكون مستوى الثقة في تقدير النموذج (99٪ ، 97.5٪ ، 95٪) أو بمعنى آخر احتمال حدوث بعض الحالات غير المواتية والتأثير في السوق يساوي 1 و 2.5 و 5٪ (المرجع نفسه).

يمكن وصف المعادلة المعروفة لـ VaR (Phelps S، 2018):

$$$(1) \ VaR (X) = \ min \ \ {x \ \ epsilon \ R: 1-F_x (-x) \ geq \ alpha \}$

حيث X عبارة عن متغير عشوائي ينفذ مقدار قيمة الحافظة ، وهو دالة توزيع تراكمية (المرجع نفسه).

من ناحية أخرى ، يشير Hooper GP (1996 ، الذي تم الاستشهاد به في Lechner و LA و Ovaert ، TC 2010) إلى VaR بثقة يحددها ألفا بطريقة أولية تمامًا:

$$$(2) \ VaR ^ \ alpha (X) = \ sigma \ sqrt {\ delta t} N ^ {- 1} \ alpha$

حيث $$$\ سيجما$هو الانحراف المعياري لعوائد الأسهم المحددة ، $$$\ دلتا ر$هو الجذر التربيعي لفترة زمنية محددة و $$$N ^ {- 1}$هي وظيفة التوزيع التراكمي (CDF) للتوزيع العادي (Lechner، LA، and Ovaert، TC 2010).

على الرغم من أن VaR هي طريقة معروفة ومعالجة لتقدير مخاطر الحافظة المحددة ، إلا أن هناك أوجه قصور في الحالة عند قياس القابلية للتأثر بقضايا السوق النهائية ، أي أن المثال يرتبط باحتمالية أحداث السوق الشديدة التي لم يتم اكتشافها بشكل مناسب التوزيع الطبيعي (Capiński ، MJ 2015). لحل هذه المشكلة ، تم إنشاء القيمة الشرطية للخطر (CVaR) والتي تأخذ في الاعتبار القيمة المتوقعة للخسارة بدلاً من VaR (المرجع نفسه). يُعرّف CVaR بأنه:

$$$(3) \ CVaR ^ \ alpha (X) = \ frac {1} {\ alpha} \ int ^ \ alpha_0 VaR ^ \ beta (X) d \ beta = \ frac {-1} {\ alpha} q ^ \ beta (X) d \ beta$

$$$(4) \ CVaR ^ \ alpha (X) = - \ frac {1} {\ alpha} (E [X 1 _ {\ {X \ leq q ^ \ alpha (x) \}}] + q ^ \ alpha (X) (\ alpha-P [X \ leq q ^ \ alpha (X)]))$

أين آن دي إتش et.al (1999 ، استشهد في Capiński ، MJ 2015) تفسير $$$-q ^ \ alpha (X)$
كما VaR من X متغير عشوائي (عودة سعر السهم) مع احتمال $$$\ alpha$وتعرف بأنها الكمية العلوية لـ X.

علاوة على ذلك ، أكد Acerbi C. و Tasche D. (2002 ، ورد ذكرهما في Capiński ، MJ 2015) ، أن "CVaR هو مقياس مخاطر متماسك". يلاحظ Rockafellar، RT، و Uryasev، S. (2000) أن CVaR لها ميزات إضافية: انتقال متكافئ ، متجانسة بشكل إيجابي ، محدب وغير ذلك.

يوضح الفصل التالي من المقالة تطبيق القيمة المعروفة للخطر (VaR) والقيمة الشرطية للخطر (CVaR) كما تم الإعلان عن النقص المتوقع (ES) في أعمال Rockafellar و RT و Uryasev، S. (2000) باستخدام تقنية المعلومات على البيانات الحقيقية.

منهجية

دع النظر في أكثر الطرق شيوعًا لحساب VaR ، وكذلك مزاياها وعيوبها.

وفقًا لتقرير Lechner و LA و Ovaert ، TC (2010) ، فإن المحاكاة التاريخية هي نهج واسع النطاق لتقييم VaR وتعديله. في النمذجة التاريخية للبيانات ، نأخذ قيم التقلبات المالية للمحفظة المعروفة بالفعل من القياسات السابقة. لذلك فإن التسلسل المنطقي هو أن عيب هذه الطريقة هو استحالة إنشاء تنبؤات للحافظات دون وجود معلومات عنها. طريقة مونت كارلو هي من نواح كثيرة مماثلة لطريقة النمذجة التاريخية ، والتي تستخدم لتقنية عالية الدقة ، والفرق الرئيسي الواضح أن حساب محاكاة مونت كارلو لا يعتمد على بيانات حقيقية ، ولكن يتم تحقيقه على قيم تم إنشاؤها بشكل عشوائي. تتمثل ميزة هذه الطريقة في إمكانية النظر في عدد كبير من المواقف ، ومحاكاة سلوك السوق في الظروف القاسية ، كما لا توجد حاجة لتقريب بين عوامل المخاطرة والتغييرات في المحفظة (Glasserman، P.، Heidelberger، P و Shahabuddin، P.، 2002). العيب الواضح هو الموارد الحاسوبية الكبيرة اللازمة لتنفيذ هذا النهج (المرجع نفسه).

بطبيعة الحال ، ليست هذه هي الطرق الوحيدة لحساب نماذج VaR. بالإضافة إلى ذلك ، هناك كلا من النماذج الخطية والتربيعية البسيطة للتنبؤ بالأسعار ، وطريقة معقدة من الاختلافات ، والتي لم يتم تناولها في المقال.

تحليل البيانات

كبيانات ثانوية لاختبار التقييم الدقيق ، يتم أخذ مخزون KAZ Minerals. لتوضيح العمل ، يتم أخذ سعر الإغلاق المعدل للمحاكاة في نموذج. إن أسهم شركة KAZ Minerals (KAZ.L) هي واحدة من الأوراق المالية الناجحة في التداول بين الشركات الكازاخستانية في بورصة لندن (LSE) وكذلك مصنفة في قائمة Premium Equity Commercial Companies (London Stock Exchange، 2019). الكيان يقدم نفسه كشركة تعدين النحاس الضخمة في كازاخستان (Kazminerals.com. 2019).

يتم تنزيل البيانات التاريخية لسعر السهم من موقع Yahoo Finance على الويب (Finance.yahoo.com ، 2019). لضمان صحة العمل ، تتم ملاحظة فترة سنة واحدة من 22 مارس 2018 إلى 22 مارس 2019. علاوة على ذلك ، لتجنب تعطل المعلومات ، في التحليل ، يتم تنزيل البيانات التاريخية لسعر سهم KAZ.L بتنسيق القيم المفصولة بفواصل (CSV) نظرًا لحقيقة أن تنسيق CSV متوافق مع برنامج Microsoft Excel (Excel) . يتم تقديم البيانات المختارة للمشروع كرسم بياني خطي باستخدام Excel في الشكل 1.

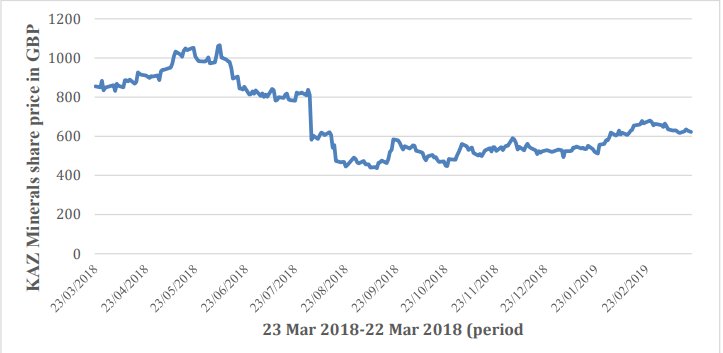
الشكل 1. ديناميكية التغيير KAZ Minerals سعر السهم لمدة سنة واحدة

نظرًا لقيود الجدول الزمني للتقرير ، بدلاً من استخدام لغة برمجة مثل Python لتنفيذ نماذج التقييم ، يتم تحليل البيانات بالكامل في Excel.

النتائج

في القسم السابق ، كانت النماذج للتنبؤ بالخسائر المحتملة في محفظة قائمة على معادلات VaR و CVaR والتغيرات المستخدمة في سعر سهم KAZ Minerals من 23 مارس 2018 إلى 23 مارس 2019 ، تم تنزيلها من مصدر الويب الرسمي Yahoo Finance (Finance.yahoo). كوم ، 2019). تم تنفيذ كلا المعادلتين لكل تاريخ من الفترة المختارة.

يوضح الجدول 1 متوسط ​​العائد اليومي للأعمال ، والانحراف المعياري للعائدات ، والحد الأدنى لقيمة العوائد والحد الأقصى لقيمة العوائد لهذا المثال.

الجدول 1. حصة يعني العودة والانحراف المعياري للعائدات

المتوسط ​​المقابل هو -0.0006 والانحراف المعياري 0.0355 من عوائد KAZ Minerals الأمنية الفريدة المحددة. ما هو أكثر من أن التباين في العوائد هو 0.0013. بالإضافة إلى ذلك ، يجب التأكيد بالتأكيد على أن عائدات الأسهم الكازاخستانية أظهرت في أعمال البحث التي أجرتها Vee و DNC و Gonpot ، P. N (2014) قيمة كبيرة في التقلبات ولكن التقدير كان مرتبطًا بمؤشر بورصة كازاخستان post post 2008. أيضا ، تجدر الإشارة إلى أن الحد الأقصى للقيمة بين العائدات هو 0.0998 ، وكذلك الحد الأدنى للقيمة بين العائدات هو -0.2829 في توزيع الخسارة. يعرض الجدول 2 الحد الأقصى والحد الأدنى للقيم بين سعر إغلاق السهم المعدل (KAZ.L) في تداول الجنيه الإسترليني (GBP) في بورصة لندن من 23 مارس 2018 إلى 22 مارس 2019.

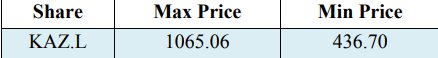
الجدول 2. الحد الأقصى والحد الأدنى لسعر سهم KAZ Minerals بالجنيه الإسترليني

والخطوة التالية هي تقييم القيمة المعرضة للخطر (VaR) والقيمة المشروطة للخطر (CVaR) لمستوى الثقة - 0.99 و 0.972 و 0.95. القيم موضحة في الجدول 3.

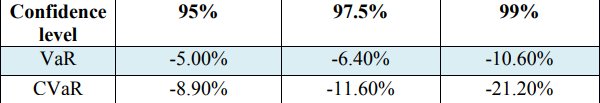
جدول 3. قيم VaR و CVaR للعائدات

يؤخذ حجم عينة المحاكاة 252 وحدة من 23 مارس 2018 إلى 22 مارس 2019 خلال سنة واحدة.

مناقشة

في التقرير ، توضح معادلات VaR و CVaR القيمة الموثوقة في حالة نماذج التقدير لسعر سهم الشركة الكازاخستانية على المدى القصير. مع وجود هذه القيم من ناحية ، تقدم كلتا الطريقتين نتائج كافية لتقييم قيمة التهديدات التي تواجهها محفظة الاستثمار (Linsmeier، TJ، and Pearson، ND 2000؛ Lechner، LA، and Ovaert، TC 2010).

علاوة على ذلك ، ووفقًا للنتائج الواردة في الجدول 2 ، فإن الإشعار التالي واضح ومباشر بأن قيم CVaR أكثر ضخامة مقارنة بقيم VaR من خلال جميع مقاييس مستوى الثقة. يمكن تقديم تفسير من خلال حقيقة أن CVaR تأخذ مخاطر متوسط ​​محفظة مختارة ، وبالتالي فهي أكثر حساسية في ذيل توزيع الخسارة من VaR. هذا يثبت مرة أخرى أن CVaR تشكل خطرًا متماسكًا (Acerbi C. and Tasche D.، 2002، cited in Capiński، MJ 2015؛ Rockafellar، RT، Uryasev، S. 2000). على سبيل المثال ، فيما يتعلق بكفاية كلا النموذجين التقديرين ، مع مستوى الثقة بنسبة 99٪ ، يوضح كل من نسبة الخطأ في القيمة (CVR) ونسبة السيرة الذاتية (CVaR) النسبة المئوية الكبيرة من الخسارة من عائدات الأسهم. للتأكد من دقتها ، قد يتم الكشف عن معدل ضربات القلب بنسبة -10.60 ٪ ونسبة الخطأ في معدل ضربات القلب هي -21.20 ٪. من الواضح تمامًا سبب التدابير الهائلة لـ CVaR بمستوى ثقة معين 99٪ نظرًا لحقيقة نطاق سعر السهم خلال هذه الفترة ، والحد الأقصى للسعر هو 1065.06 جنيهًا إسترلينيًا ، وسعر السهم الأدنى هو 436.70 جنيهًا إسترلينيًا ، على التوالي.

استنتاج

بعد النظر في كل ما سبق ، يجب أن نذكر مرة أخرى بوضوح أن الهدف من هذا التقرير هو إظهار تقدير قيمة الخسارة المحتملة للشركة الكازاخستانية (KAZ Minerals) على مدى فترة من 23 مارس 2018 إلى 22 مارس 2019. المشكلة على معادلات القيمة المعرضة للخطر (VaR) والقيمة الشرطية للخطر (CVaR). تتم مقارنة الأداء من المحاكاة مع بعضها البعض في نفس الفترة الزمنية. تُظهر النتائج القيمة المهمة لكل طريقة وتُثبت العمل السابق في نفس المجال الذي يحتوي على CVaR مقاييس أكثر دقة مقارنةً بـ VaR (Acerbi C. and Tasche D.، 2002 ، المذكورة في Capiński ، MJ 2015 ؛ Rockafellar، RT ، وأورياسيف ، S.2000).

على الرغم من الانتقادات ، تعد VaR أداة واسعة الانتشار في جميع المؤسسات المالية حتى يومنا هذا وهناك مجموعة واسعة من نسخة التعديل الخاصة بها. نظرًا لعقبات الحساب المعقد في البحث العميق ، يتم إجراء التجربة باستخدام Microsoft Excel بدلاً من استخدام لغة برمجة مثل Python ، فضلاً عن النتائج الموضحة في التقرير. نتائج المقال قادرة على أن تكون أساسًا لمزيد من العمل في استخدام مقياس تقييم معقد للمخاطر بالنسبة للمحفظة في صناعة البورصة وقطاع التأمين وصناعة الاستثمار.