فيما يلي سوف نقول بضع كلمات حول البديل المنفصل للنماذج الرياضية في شكل معادلات تفاضلية خطية ، والتي تُعرف عمومًا ولكنها غير متوقعة إلى حد ما بالنسبة للمهندسين ، أي نماذج الانقلاب الذاتي - المتوسط المتحرك ، والآفاق غير المعتادة للغاية لمثل هذه النماذج ، والتي تتجاوز قدراتها بشكل كبير ما اعتدت على الحصول عليه من LDU.
تشمل قائمة الإمكانات المحتملة للتكنولوجيا تحليل الأنظمة التي يتعذر الوصول إليها من أجل اضطراب وارد للمراقبة وتحديد خواص الرنين لهذه الأنظمة والطيف وعملية الإثارة الخارجية والتقدير الطيفي للعمليات من خلال تحقيقاتها القصيرة ونمذجة سلوك الأنظمة بتردد أخذ العينات المنخفض بمرور الوقت ، إلخ.

عمليات ARMA ، المعروفة جيدًا للاقتصاديين (بتعبير أدق ، "علماء الاقتصاد") ، ليست معروفة كثيرًا للمتخصصين في التنظيم التلقائي ، وفي رأيي ، بالكاد يستخدمها المهندسون الميكانيكيون والمهندسون الإلكترونيون الراديويون ، وخاصة "المدرسة القديمة". يحاول المقال الإشارة إلى بعض المجالات المحتملة لتطبيق نظرية ARMA في الممارسة الهندسية.
باختصار ، مبسطة ، بالنسبة لأولئك الذين ليسوا على دراية بالموضوع ، حول أيهما في الواقع. عادةً ما تتطابق العملية الزمنية العشوائية x (t) للأسباب "الرقمية" الواضحة في الممارسة العملية مع تسلسل الوقت المنفصل x [i] مع الفاصل الزمني لأخذ العينات Δt.
من حيث المبدأ ، بالنسبة لأي عملية x [i] يمكن تمثيل الشكل
x [i] - a 1 · x [i-1] - a 2 · x [i-2] - ... - a p · x [ip] = b 0 · f [i] + b 1 · f [i- 1] + ... + b q · f [iq] (1) ،
حيث
k و b
k ثابتان (بالنسبة لهذا النموذج) معاملات ، تسمى نموذج المتوسط المتحرك للانعكاس بترتيب الانتهاك الذاتي p والمتوسط المتحرك q. أو نموذج ARMA (p ، q) ، f [i] هو نوع من العملية "الواردة" ، والتي تكون أقل قليلاً منها. في كثير من الأحيان (1) مكتوبة في شكل مختلف قليلا (6).
في الأساس ، إنه مجرد مرشح رقمي يحتوي على أجزاء AR متكررة وأجزاء MA غير متكررة.
هناك تطابق بين نماذج ARMA (p ، q) والأنظمة الخطية (على سبيل المثال ، ميكانيكية) ، على سبيل المثال ، الموصوفة في المعادلة التفاضلية الخطية المعروفة للنموذج
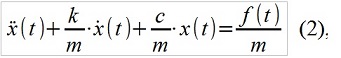
حيث m ، c ، k هي كتلة النظام الميكانيكي وصلبته وتثبيته ، f (t) هي القوة الخارجية. النظير ARMA يشبه هذا:
x [i] - a 1 · x [i-1] - a 2 · x [i-2] = b 1 · f [i-1] (3) ،
يمكن العثور بسهولة على معاملات النموذج من خلال القيم الذاتية λ
1 و *
1 * (للإيجاز ، نعتبر الحالة "المتأرجحة") للنظام الخطي و Δt
a
1 = z + z * ، a
2 = - z · z * ، b
1 = j (z * -z) · /t / (2mω
1 ) ،
حيث z = exp (λ
1 · Δt) ، =
1 = -ε
1 + jω
1 ، j هي الوحدة التخيلية ، * هي الاقتران المعقد
للرجوع اليها:

لنظام الاختبار ، م = 1 كجم ، ج = 100 ن / م ، ك = 0.75 كجم / ثانية ، =t = 0.12 ثانية ،
تم الحصول عليها ARMA (2،1) -النموذج
x [i] - 0.69433x [i-1] +0.91393 x [i-2] = 0.010696f [i-1](شرح موجز للغاية عن كيفية الحصول على (3) من (2). وظيفة انتقال النبضة في نظامنا الخطي ، أي استجابة النظام لنبضة واحدة:
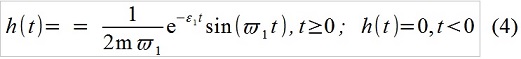
ويسمى السجل (2) في النموذج "المتكامل" "الالتفاف" f (t) و h (t) ، وهذا يعني أنه ينطوي على النظر في الإجراء الخارجي باعتباره سلسلة من الدوافع الأولية. في وقت منفصل ، الكتابة ، حسنا ، على سبيل المثال ، مثل هذا:
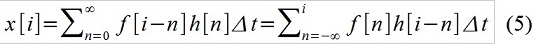
عن طريق إضافة x [i] و x [i-1] و x [i-2] باستخدام العوامل المحددة 1 و
1 و
2 ، فإنها تحقق الإبادة المتبادلة لـ "ذيول" لا حصر لها ، تبقى [i] - f [i] على الجانب الأيمن · H [0] = f [i] · 0 و f [i-1] · h [1] = f [i-1] · b
1 . من وجهة نظر نظرية ARMA ، يتحول النموذج اللانهائي الأبعاد لمتوسط المتحرك MA (∞) إلى ARMA (2،1) (على الرغم من أن البعض سيقولون إنه تم الحصول على نموذج الانحدار الذاتي المحض AR (2) = ARMA (2،0) عن طريق الصدفة.
ملاحظة 1. سيقول القارئ الذي يكون على دراية بالمعالجة الرقمية للعمليات أن تقدير h (t) ليس صحيحًا تمامًا - من الضروري قصر الوظيفة h (t) بالتردد على 1 / (2Δt) (مرشح). خلاف ذلك ، هناك خطأ في إخفاء التردد. توضح الرسوم البيانية لاستجابة التردد واستجابة الطور لنظامنا ، "الطرازي" ونماذج ARMA ، سبب احتمال إهمال هذا الخطأ في معظم الحالات الهندسية (الشكل 1) (هنا ، استجابة التردد على مقياس لوغاريتمي).
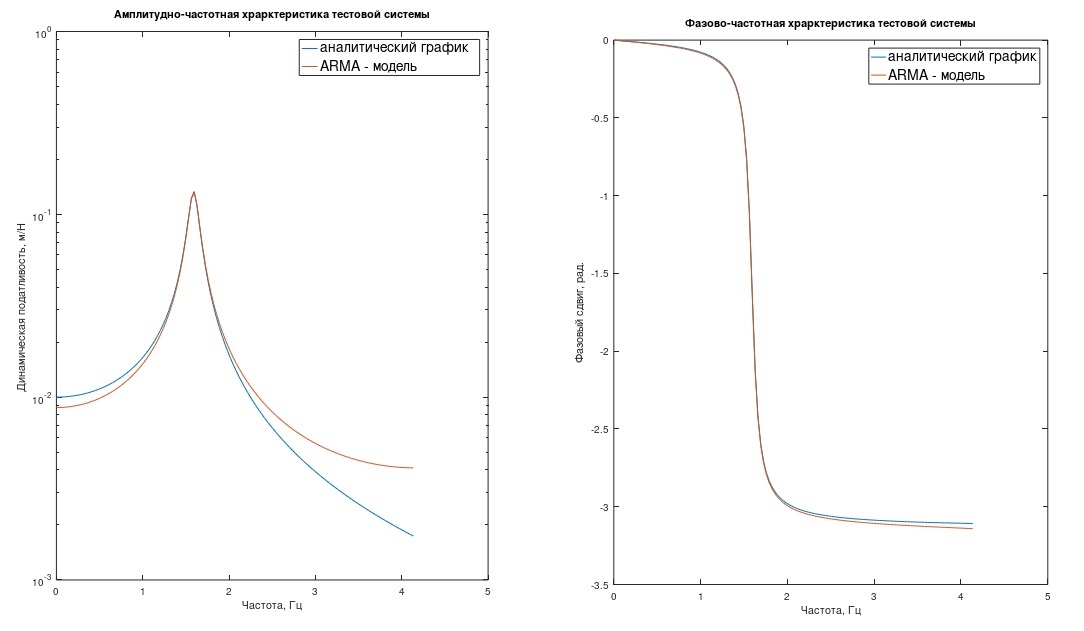
الشكل 1: استجابة التردد واستجابة المرحلة لنظام الاختبار.
ملاحظة 2. في الممارسة العملية ، يمكن أن يكون ترتيب نموذج ARMA أكبر بكثير من المثال المذكور أعلاه ، على سبيل المثال ، بسبب درجات متعددة من حرية النظام الميكانيكي أو طيف معقد من التأثير الخارجي الحقيقي.
ملاحظة 3. مهم جدا. هناك طرق (لم يتم النظر فيها هنا - يمكن كتابة العديد من المقالات عنهم) التي تسمح لأحد بتقدير المعلمات من نموذج ARMA (أي ترتيب النموذجين p و q ومعاملات
k و b
k ) فقط من خلال العملية الناتجة x [i] ، وفقًا للافتراض هذا f [i] هو ضوضاء بيضاء افتراضية يمكن تقدير اختلافها أيضًا. بشكل عام ، مثل هذا التقييم هو الجزء الرئيسي من نظرية ARMA بأكملها. في حين أن هذه الأساليب لا تختلف في حد معين ، فإنها ذات أهمية كبيرة.
الآن عن السبب ، في الواقع ، كل هذا يمكن (أو يمكن) أن يطبق في الممارسة. بالإضافة إلى الوضوح الواضح - الإنشاء السريع للجيوب الأنفية "المبطنة" (غير المموجة) من النقطتين الأوليين ومعاملتين أ
1 و
2 ، هناك ، في رأيي ، تطبيقات أكثر جدية لهذه النماذج في الممارسة الهندسية.
1. حسنًا ، في الواقع ، لمحاكاة تشغيل النظام - نعطي إشارة خارجية حقيقية f [i] إلى المدخلات ، نحصل على x [i] في الخرج:
x [i] = a 1 · x [i-1] + a 2 · x [i-2] + ... + a p · x [ip] + b 0 · f [i] + b 1 · f [i- 1] + ... + b q · f [iq] (6)
يتكيف نموذج ARMA مع المهمة بشكل أفضل من نموذج الفرق المحدود ، ومع ذلك ، فإن هذا ملحوظ فقط في فترات أخذ العينات الكبيرة. (في الشكل 2 ، Δt = 0.12 ثانية (يسار) و 0.03 ثانية). في أي الحالات يكون من المنطقي أن تعبث مع ARMA - أنت تقرر ذلك.
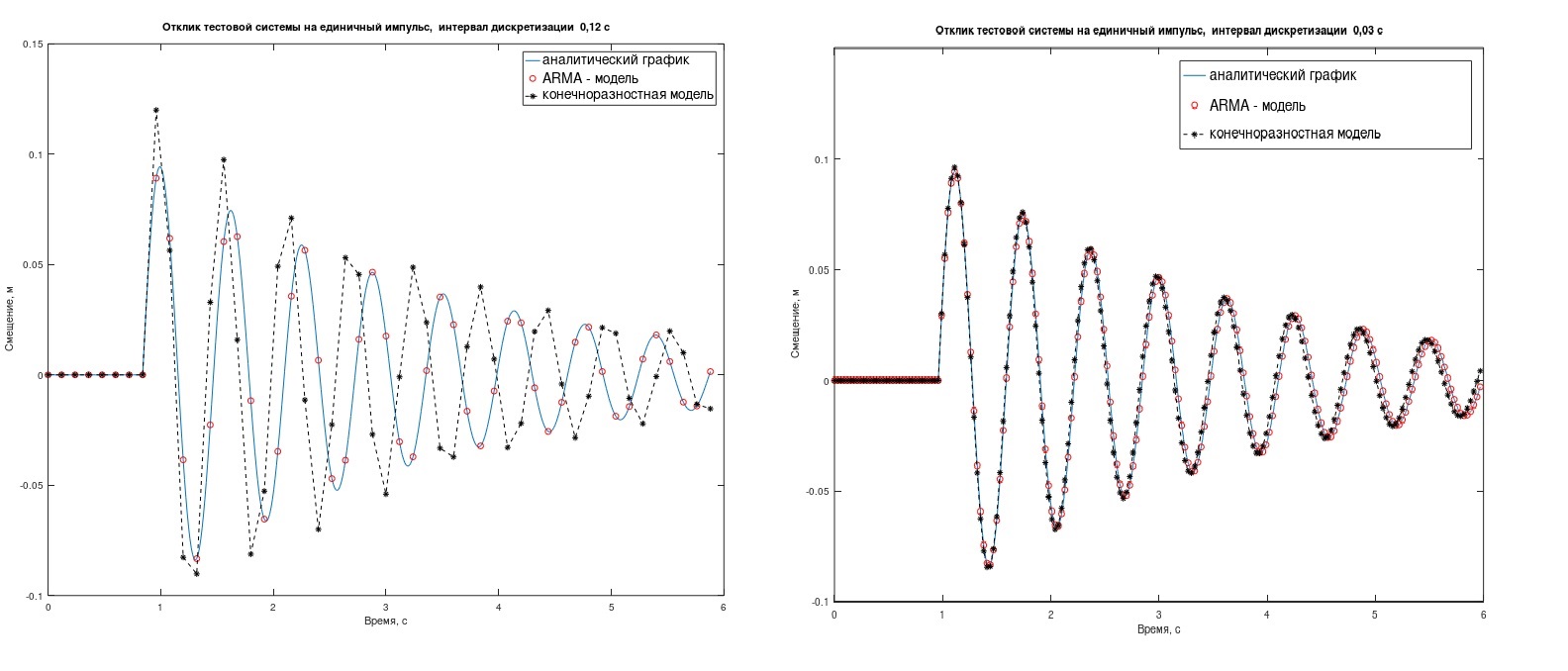
التين. 2. استجابة أنظمة الاختبار إلى دفعة واحدة.
2. من أجل التقدير الطيفي ، لا سيما عندما يكون طول تنفيذ العملية الثابتة غير كافٍ للمراقبة. ربما هذا هو التطبيق الهندسي الأكثر شهرة لنماذج ARMA. نظرًا لأنه سيتم الحصول على مرشح رقمي معين وتباين الضوضاء البيضاء التي تدخله للعملية قيد الدراسة ، فإن مهمة بناء تقدير PSD يتم حلها بطريقة واضحة. في الواقع ، من الممكن الحصول على رسوم بيانية SPM "سلسة" للغاية من الخارج وفي نفس الوقت خلق انطباع بدقة عالية. يرتبط التحسن المتوقع في التقييم بحقيقة أن الباحث يقدم معلومات خارجية حول طبيعة العملية إلى إنشاء التقييم - عادةً عن طريق تحديد نموذج نموذجي معروف.
باختصار ، أنت بحاجة إلى معرفة الشكل الذي يجب أن تظهر به PSD. لا يمكن للدراسات "الاستكشافية" لهذا التطبيق باستخدام الأساليب الكلاسيكية أن تفعل شيئًا كبيرًا ، وغالبًا ما تشير إلى الدراسات الكلاسيكية (استنادًا إلى FFT) ذات الطبيعة المتشابهة ، ولكنها تحقق إنجازات أطول بكثير. هناك فرصة الأخطاء الجسيمة.
3. لتحليل خصائص الرنين للنظام وطيف العمل الخارجي ، في حالة عدم توفر التأثير الخارجي الحقيقي للمراقبة. كما ذكرنا سابقًا ، من الممكن ، مع العلم بالعملية x [i] ، تحديد جميع معاملات النموذج a
k و b
k (وتباين الضوضاء البيضاء الواردة). باستخدامهم ، وتحديد جذر متعدد الحدود مع المعاملات المقابلة ، من السهل العثور على "أقطاب" و q "الأصفار" للنموذج (λ
k و μ
k ) وإنشاء وظيفة النقل - ربما لا يمكنك حتى استخدام نموذج ARMA (هنا) بالنظر إلى ذلك ، وفي النموذج "التحليلي" المعتاد - كما هو موضح أعلاه (الشكل 1) ، يكون الفرق صغيرًا. على سبيل المثال ، بالنسبة إلى p = 5 ، q = 3 (في حين نستخلص من القيود الحالية ، على ما يبدو ، على نسبة p و q) ، كخيار ، لدينا:
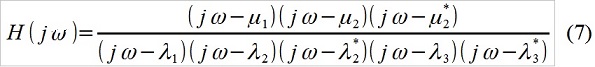
كل شيء بسيط للغاية ، بالطبع. استنادًا إلى الطبيعة المعروفة للكائن قيد الدراسة (على سبيل المثال ، هذه هي اختبارات المضلّع لسلاسة ركوب السيارة) وتأثيرها الخارجي (ملف microprofile للطريق) ، قرر الباحث إعادة كتابة وظيفة النقل ، على سبيل المثال ، مثل هذا:
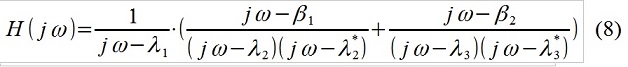
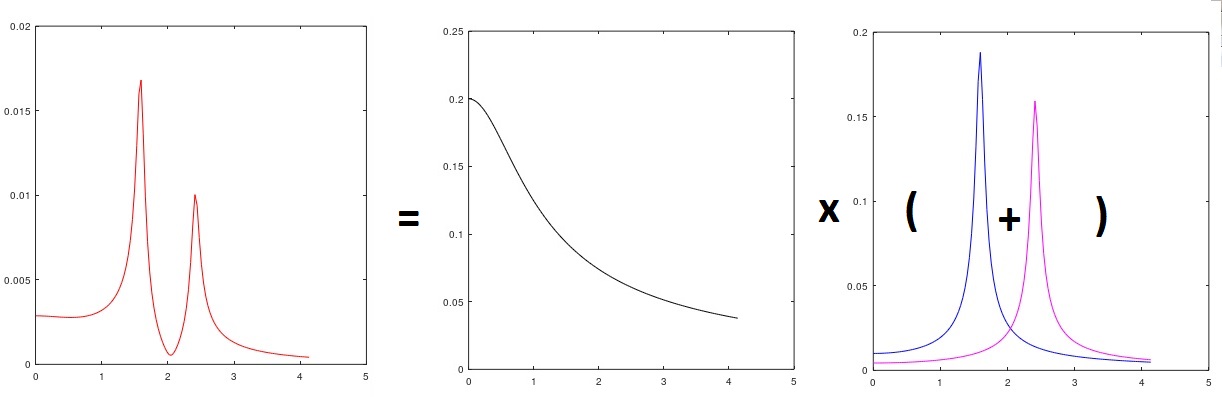
الشكل 3: تحليل طيف الإشارة مع توزيع الاضطراب الوارد
والتعليق - جزء النموذج المتعلق بـ λ
1 هو بوضوح (ما يصل إلى التربيع والضرب من خلال تباين الضجيج الأبيض الافتراضي الوارد) ، الملف المجهر "الوردي" للطريق (الشكل 3) (أي ، حددنا طيفًا غير معروف من الحقيقي إشارة الدخل - تم اختيارها يدويًا - يبدو أنها "متشابهة") ، λ
2 و λ
3 هي خصائص الرنين للجسم على التعليق (ربما وسائط طولية وزاوية ورأسية للاهتزاز). المشكلة الأساسية ، بالطبع ، هي تحديد معلمات نموذج ARMA. بالنسبة للموصوفة للتو ، يمكنك أحيانًا ، دون أي ARMA ، "الزحف" بالطريقة القديمة (وإن كانت في شكل إلكتروني) وفقًا للرسم البياني للكثافة الطيفية وقياس عرض الذروة بمستوى -3 ديسيبل ، إلخ ، أو تطبيق التقويس ، وأحيانًا بنجاح كبير .
3. للتنبؤ الخطي x [i]. على ما يبدو ، فإن التطبيق الرئيسي لل ARMA هو لعلماء الاقتصاد. يمكن ملاحظة من (6) أنه إذا تم تقدير معاملات النموذج باستخدام الطرق الموضحة أعلاه ، يمكن تقدير القيمة التالية x [i] بدقة لضوضاء بيضاء افتراضية يتعذر الوصول إليها للمراقبة b
0 · f [i] ، يتم تقدير تباين هذه الضوضاء البيضاء جنبا إلى جنب مع معاملات النموذج. عادةً في هذه الحالة ، يتم الضبط الديناميكي (في الوقت الفعلي) لمعلمات النموذج. على ما يبدو ، يمكن أن يكون مفيدًا في أنظمة الاهتزاز النشط والحد من الضوضاء. المتخصصين TAP يعرفون أفضل.
4. لاستعادة عملية يتعذر الوصول إليها لا يمكن ملاحظتها. عند تقسيم النموذج إلى أجزاء ، كما هو موضح أعلاه في القسم 3 ، استنادًا إلى المعرفة حول طبيعة العملية قيد الدراسة ، يمكن إجراء تقييم منفصل لطيف الاضطراب الوارد ، وبشكل منفصل ، الخصائص التذبذبية للنظام المادي (فصل النموذج إلى أجزاء). يمكنك أن تذهب أبعد من ذلك - إنشاء عامل تصفية (نموذج ARMA ، معكوس النموذج الأصلي) الذي يربط إخراج النظام مع المدخلات ، وبمساعدته من العملية الناتجة x [i] الحصول على تنفيذ مؤقت للاضطراب الوارد. على سبيل المثال ، حاول استعادة إشارة غير مشوهة مسجلة بتشوهات خطية غير معروفة بدقة بواسطة جهاز غير متاح لدراسة منفصلة (على سبيل المثال ، تم الحصول عليها بواسطة القياس عن بُعد).
بناءً على معرفتي المتواضعة ، كنتيجة لذلك سأعبر عن هذا الحكم الذاتي. يعتمد قابلية تطبيق تقنيات ARMA على المشكلات الهندسية اعتمادًا كبيرًا على كمال طرق تقدير معلمات هذه النماذج من الإشارة الناتجة ، أو في رأيي ، يتم تقييدها بشدة بسبب عيوب هذه الطرق. يبدو أن تراكم الخبرة في تطبيق ARMA في الهندسة أمر منطقي ، بشكل أساسي ، تحسباً لحدوث "انفراج" محتمل جدًا في هذا المجال.