مقدمة

أعتقد أننا بحاجة إلى شرح موجز لمفاجأة هذا الموضوع الذي يبدو تافهاً مع حساب ميزانية الطاقة ولماذا الأقمار الصناعية CubeSat بالضبط؟ حسنًا ، كل شيء بسيط هنا: لقد أظهرت ممارستي التعليمية القصيرة (بالنسبة لي) أن هذا الموضوع ، على الرغم من كونه أساسيًا ، كان بعيدًا عن أن يفهمه الجميع في المرة الأولى ، وعلاوة على ذلك ، فقد كان لديه عدة أسئلة لم تكن واضحة في القراءة الأولى. علاوة على ذلك ، يبدو أنه في مثل هذه الأشياء الأساسية ، ما زالوا ينشرون مقالات في IEEE وهذا بعيد عن أن يقوم به الطلاب . لماذا بالضبط CubeSat؟ لا يزال الأمر أبسط هنا: تنسيق القمر الصناعي مثير للاهتمام (حقيقة وجود السواتل الصغيرة والمتناهية الصغر ، كما اتضح فيما بعد ، تغرق الكثيرين في حالة صدمة قصيرة) ، وبالتالي فهي مناسبة للغاية للأغراض التعليمية.

سيتم تنفيذ المحاكاة في بيثون 3 للأسباب نفسها التي عبرت عنها في منشوري السابق . سننظر في حالة المدار المنخفض (LEO - المدار الأرضي المنخفض) ، ونحسب ، في الواقع ، نسبة الإشارة إلى الضوضاء (نسبة الإشارة إلى الضوضاء - نسبة الإشارة إلى الضوضاء) عند دخل المستقبِل عبر وصلة هابطة (DL - وصلة هابطة). سوف نستخدم العديد من الدلائل من الوصول المفتوح وبناء الرسوم البيانية للوضوح.

تتوفر جميع أكواد المصدر في مستودع جيثب الخاص بي ، وأدعو جميع المهتمين بقراءتها! سأكون ممتنا للغاية لمراجعة الكود والنقد البناء!

دعنا نذهب!

ما الصيغ سوف نحسب؟

أولاً ، بالطبع ، هذه صيغة معروفة لنسبة الإشارة إلى الضوضاء على مقياس لوغاريتمي (بالديسيبل ، ببساطة) للجميع (المشاركين في الموضوع) ، حيث نأخذ في الاعتبار جميع الخسائر والتضخيمات المحتملة مع قدر معين من التجريد:

$SNR = P_t + G_t + G_r + \ eta_ {t} + \ eta_ {r} - L_r - L_t - L - L_ {add} - N [dB] \ qquad (1)$

حيث - القدرة الكلية للضوضاء الحرارية (لها علاقة معروفة بالكثافة الطيفية للضوضاء $N_0 = kT_ {ضجيج}$ ) بالديسيبل (ديسيبل لكل مللي واط) ، P_t - القدرة المرسلة بالوحدة dBm ، G_t و G_r - كسب الهوائي على جانب المرسل والمستقبل ، على التوالي (بالديسيبل - ديسيبل متناحية الخواص) ، $\ eta_ {t}$ و $\ eta_ {r}$ - كسب مرسل التغذية والمستقبل (بالوحدة dB) ، L_t و L_r - خسائر في وحدات التغذية (بالديسيبل) ، الخسائر في طريق انتشار الموجة الكهرمغنطيسية بالديسيبل ، $L_ {add}$ - خسائر إضافية (إذا جاز التعبير ، بعض الهامش) بالديسيبل.

بشكل عام ، مع المصطلحات السبعة الأولى ، يكون الأمر أكثر وضوحًا: هذه بيانات مرجعية. الأمور أكثر إثارة للاهتمام مع آخر ثلاثة مشاركين في هذه العملية.

قوة الضوضاء الحرارية

كما تعلمون ، لا يوجد مكان للاختباء من هذه الآفة من الأجهزة الإلكترونية ، يمكنك فقط مراعاة:

$N = 10lg \ left (\ frac {kT_ {noise} B_ {noise}} {10 ^ {- 3}} \ right) [dBm] \ qquad (2)$

حيث - بولتزمان ثابت $T_ {noise} = T_a + T_e$ - درجة حرارة الضوضاء المكافئة ، T_a - مجموع خسائر الهوائي والضوضاء (الخلفية) في السماء ، $T_e = T_0 (F_ {sys} -1)$ - درجة حرارة ضوضاء المستقبل ( T_0 = 290 كيلو بايت و $F_ {sys} = 10 ^ {\ frac {NF} {10}}$ - رقم الضوضاء ، والذي يمكن تقديره من صورة الضوضاء ( - رقم الضوضاء) لهوائي الاستقبال) ، و $B_ {الضوضاء}$ - عرض نطاق تردد الضوضاء. يمكنك أن تأخذ نطاق الضوضاء مساوياً لعرض النطاق الترددي للمستقبل نفسه ومع ذلك ، وفقًا لـ [1 ، صفحة 98] عرض النطاق الترددي الضوضاء $B_ {الضوضاء}$ يمكن تصنيفها بدقة أكبر بقليل $\ جاما ب$ حيث $\ جاما$ - ثابت من 1.002 إلى 1.57 (يتعلق بتهيئة المستقبل).

خسائر إضافية

هنا يمكنك إما الحصول على نوع ما من الإمداد المضمون ، أو الحصول عليه ، كقاعدة عامة ، من نفس الأدلة ، أو التعمق وحساب كل شيء بنفسك.

في هذا القسم ، أعتمد كليًا تقريبًا على كتاب كانتور القديم الجيد ، أي هذا الجزء منه [1 ، ص 88-96]. إذا كان لدى القراء مصادر موثوقة أكثر صلة - يرجى المشاركة ، وأعتقد أنه سيكون مفيدًا للجميع.

ما نلفت الانتباه في المقام الأول إلى:

الخسارة الناجمة عن الانكسار وعدم دقة توجيه الهوائي ( خسارة حزمة الهوائي )

تم تعيينها على أنها $L_b = 10log_ {10} (1+ (2 \ theta / \ theta_ {0.5}) ^ 2)$ حيث $\ ثيتا$ - عرض شعاع و $\ theta_ {0.5}$ - عرض حزمة نصف القدرة ، وتعتمد ، بغض النظر عن مدى صعوبة التخمين ، على خصائص بعض أجهزة الهوائي:

آثار المرحلة الجوية

إذا كنت تعتقد أن الكلاسيكية ، فإن هذه الخسائر تؤثر في المقام الأول على معدل نقل البيانات بسبب عرض النطاق الترددي لجهاز الاستقبال ، لأنه من المستحسن اختيار النطاق وفقا للجدول 1 [1 ، ص. 91]. لتجنب تشويه المرحلة.

علامة التبويب. 1. الحد الأقصى لعرض النطاق الترددي المتلقي لنطاقات مختلفة.

تردد الناقل ، غيغاهرتز	0.5	1	5	10
عرض النطاق الترددي للمستقبل (B) ، ميغاهيرتز	10	25	270	750

ومع ذلك ، تجدر الإشارة إلى أن الأرقام مؤثرة للغاية وغالبًا ما لا يتم أخذها في الاعتبار ، بسبب الضوضاء الحرارية.

الخسارة الناجمة عن عدم تطابق استقطاب الهوائي

يمكن تقديره وفقًا لمعاملات الاهليلجيه $e_1$ و $e_2 دولا$ (أرفق قصاصة من الكتاب السوفيتي بالشكل 1).

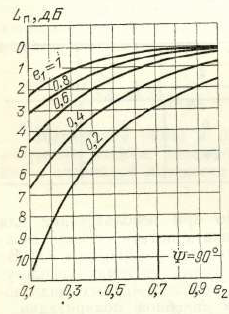
الشكل 1. اعتماد الخسائر الناتجة عن عدم تطابق الاستقطاب بين هوائيات الإرسال والاستقبال على الإهليلجية. [1 ، ص. 93]

ومع ذلك ، صادفت هذه المعلمة كمرجع. على سبيل المثال ، عند حساب ميزانية الطاقة لـ NanoCom AX100 ، تكون خسارة الاستقطاب 3 dB (الخسارة الجوية 2.1 dB ، الخسارة الأيونوسفيرية 0.4 dB).

التوهين الجوي

يمكننا تقييم هذه المعلمة المهمة إما وفقًا لتوصيات الاتحاد ، أو حسابها بأنفسنا. لحسن الحظ ، هناك مكتبات خاصة مثل هذه المكتبة.

التوهين على طول طريق انتشار الموجة الكهرومغناطيسية (خسارة المسير)

دون مزيد من اللغط ، نطبق صيغة فريس لتبدأ بـ :

$L = 20lg \ frac {\ lambda} {4 \ pi d} [dB] \ qquad (3)$

حيث $\ امدا$ - الطول الموجي الكهرومغناطيسي (يتعلق بطريقة معروفة بتردد الموجة الحاملة $f_0 = \ frac {c} {\ lambda}$ . هي سرعة الموجة الكهرومغناطيسية (سرعة الضوء ، إذا كانت أبسط)) ، و - المسافة بين الأقمار الصناعية والمحطة الأرضية.

وهنا نأتي ، ربما ، إلى السؤال الأكثر إثارة للاهتمام: ما المسافة التي يجب أن نتخذها لإجراء العمليات الحسابية؟ كما ذكرنا سابقًا في المقدمة ، نحن نفكر في سواتل LEO ، مما يعني أن قمرنا الصناعي المزعوم يتحرك بالنسبة إلى الأرض (على عكس الحالة الثابتة بالنسبة للأرض ، حيث يكون القمر الصناعي ، كما كان ، معلقًا فوق نقطة واحدة).

يمكنك ، بالطبع ، تبسيط كل شيء قدر الإمكان ، مع الأخذ في الاعتبار المخطط (الشكل 2) ، عندما يُفترض أن مدار ساتل الاتصالات يقع ، "تقريبًا ، فوق رأس" محطتنا الأرضية.

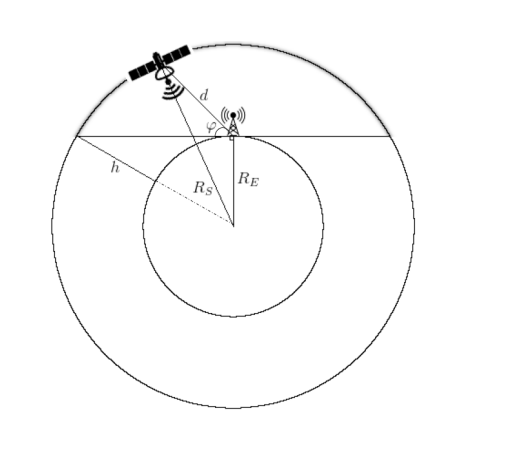
التين. 2. وصف تخطيطي لمسار CubeSat في مدار أرضي منخفض [2].

ثم يمكن حساب المسافة بالصيغة:

$d = \ sqrt {(R_E + h) ^ 2-R_E ^ 2cos ^ 2 \ phi} - R_Esin \ phi \ qquad (4)$

حيث R_E - في الواقع ، نصف قطر الأرض ، - ارتفاع مدار الساتل ، و $\ فاي$ - زاوية الارتفاع.

ومع ذلك ، يمكنك البخار أكثر من ذلك بقليل ، والعودة مرة أخرى إلى الكلاسيكية (مختلفة بالفعل) [3 ، ص .110-123] وحساب كل ما يتعلق بالفعل بالإحداثيات الجغرافية الحقيقية للمحطة الأرضية (
$lat_ {gs}$ و $long_ {gs}$ ) والموقع الفعلي للقمر الصناعي (عقدة تصاعدية فورية - $L_ {عقدة}$ والقطب المداري - القطب مدار لحظية أنا ). استعد ، سيكون هناك الكثير من علم المثلثات:

$d_ {min} = R_E \ frac {\ sin \ lambda_ {min}} {\ sin \ eta_ {min}} \ qquad (5)$

حيث $\ sin \ lambda_ {min} = \ sin (90 ^ 0 - i) \ sin (lat_ {gs}) + \ cos (90 ^ 0 - i) \ cos (lat_ {gs}) \ cos (long_ {gs} - (L_ {node} - 90 ^ 0))$ - أدنى زاوية مركزية للأرض ، $\ eta_ {min} = arctan \ frac {\ sin \ rho \ sin \ lambda_ {min}} {1 - \ sin \ rho \ cos \ lambda_ {min}}$ - الحد الأدنى لزاوية النظير ، $\ rho = arcsin \ frac {R_E} {R_E + h}$ هو دائرة نصف قطرها الزاوي للأرض. يمكن حساب المسافة القصوى من خلال:

$d_ {max} = R_E \ frac {\ sin \ lambda_ {max}} {\ sin \ eta_ {max}} \ qquad (6)$

حيث $\ sin \ eta_ {max} = \ sin \ rho \ cos \ epsilon_ {min}$ و $\ lambda_ {max} = 90 ^ 0 - \ epsilon_ {min} - \ eta_ {max}$ ( $\ epsilon_ {min}$ - الحد الأدنى لزاوية ارتفاع الساتل).

لتلخيص ملخص قصير للمعلمات :

ما نختاره كنقاط انطلاق : تردد الموجة الحاملة ، ارتفاع المدار (ربما موقع القمر الصناعي والإحداثيات الجغرافية للمحطة الأرضية - يعتمد على الدقة التي نريد الحصول عليها) ؛
نجد المعلمات التي تعتمد على المعدات والقابلة للتعديل : الطاقة المنقولة ، عرض النطاق الترددي المتلقي.
نجد بيانات مرجعية : كسب الهوائي وفقدانه ، كسب وخسارة وحدة التغذية ، درجة حرارة الضوضاء ، خسارة إضافية.

نحن محاكاة ما حدث نتيجة لذلك

كمصدر للمعلمات التقنية لتقييم الوصلة الهابطة ، لدينا أمثلة واقعية متاحة لأجهزة الإرسال والاستقبال والهوائيات لسواتل CubeSat ، مثل NanoCom AX100 و NanoCom ANT430 . بالنسبة إلى النطاقات الأكبر حجماً ، من الأفضل بالطبع التفكير في النطاق S-band . يتوفر هوائي التصحيح NanoCom ANT2000 وجهاز الإرسال والاستقبال NanoCom SR2000 لهذا النطاق.

نبدأ في التحقق مما حدث.

from SmallSatLB import * import pandas as pd

كل المنطق مقسم إلى خيارين: 'مسودة' ، تستخدم فيها الصيغة (4) لحساب المسافة ؛ و "دقيق" ، حيث يتم استخدام الصيغ (5) و (6).

'مشروع'

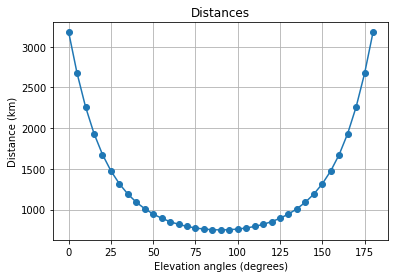
 l_d = LinkBudget(750*1e3, 'draft') #   (   ) d = l_d.distance() #   phi = np.pi*np.array(range(0,181,5))/180 #     plt.plot(180*phi/np.pi, d*1e-3, '-o') plt.title('Distances') plt.xlabel('Elevation angles (degrees)') plt.ylabel('Distance (km)') plt.grid()

 snr, EIRP = l_d.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000) #  SNR plt.title('Expected SNRs') plt.xlabel('Elevation angles (degrees)') plt.ylabel('SNR (dB)') plt.legend() plt.grid()

الجمال!

"دقة"

 l_p = LinkBudget(750*1e3, 'precise',\ L_node = 100+90, incl = 90 - 61.5,\ lat_gs = 22, long_gs = 200, eps_min = 5) snr, EIRP = l_p.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000) print(min(snr)) print(max(snr))

 >>> 5.556823874020452 >>> 8.667000351847676

بشكل عام ، هنا: لدينا أداة صغيرة لإجراء "تقديرات" أولية وحسابات لمدى ضعف الإشارة ، بينما تنتقل من القمر الصناعي إلى الأرض (أو العكس).
شكرا لكم جميعا على اهتمامكم!

قائمة الأدبيات المستخدمة :

Kantor L. Ya.، Askinazi G.B. اتصالات الأقمار الصناعية والبث: كتاب مرجعي . - الراديو والاتصالات ، 1988.
Otilia Popescuy ، و Jason S. Harrisz و Dimitrie C. Popescuz ، تصميم النظام الفرعي للاتصالات لمهمات المكابح الساتلية المتناهية الصغر: المنظور التشغيلي والتنفيذي ، 2016 ، IEEE
Wertz JR، Larson WJ Space Mission Analysis and Design، Space Technology Library. - Microcosm Press and Kluwer Academic Publishers، El Segundo، CA، USA، 1999.

نحن نحسب ميزانية الطاقة لخط الراديو لقمر تنسيق CubeSat