الديناميكا الحرارية للثقوب السوداء

يوم سعيد لرواد الفضاء! سلمنا إلى المطبعة كتابًا صغيرًا عن الثقوب السوداء . في هذه الأيام ، أظهر علماء الفيزياء الفلكية للعالم كله كيف تبدو الثقوب السوداء. صدفة؟ لا نعتقد ؛) لذا ، انتظر ، قريباً سيظهر كتاب مذهل ، كتبه ستيفن جاسر وفرانس بريتوريوس ، ترجم من قبل عالم الفلك بولكوفو الرائع المعروف أيضًا باسم Astroded كيريل ماسلنيكوف ، قام الأسطورة فلاديمير سوردين بإجراء تحرير علمي ودعمت مؤسسة المسار نشره.

مقتطفات "الديناميكا الحرارية من الثقوب السوداء" تحت خفض.

حتى الآن ، نظرنا في الثقوب السوداء ككائنات فيزيائية فلكية تشكلت أثناء انفجارات المستعرات الأعظمية أو تقع في مراكز المجرات. نلاحظهم بشكل غير مباشر ، ونقيس تسارع النجوم القريبة منهم. أصبح التسجيل الشهير لموجات الجاذبية بواسطة جهاز استقبال LIGO في 14 سبتمبر 2015 مثالًا على مزيد من الملاحظات المباشرة عن تصادمات الثقب الأسود. الأدوات الرياضية التي نستخدمها لاكتساب فهم أفضل لطبيعة الثقوب السوداء هي: الهندسة التفاضلية ، معادلات آينشتاين والأساليب التحليلية والرقمية القوية المستخدمة في حل معادلات آينشتاين ووصف هندسة الزمان والمكان التي تنشئها الثقوب السوداء. وبمجرد أن نتمكن من إعطاء وصف كمي كامل للزمان والمكان الناتج عن الثقب الأسود ، من وجهة النظر الفيزيائية الفلكية ، يمكن اعتبار موضوع الثقوب السوداء مغلقًا. في منظور نظري أوسع ، لا يزال هناك العديد من الفرص للبحث. الغرض من هذا الفصل هو التحدث عن بعض الإنجازات النظرية لفيزياء الثقب الأسود الحديثة ، حيث يتم دمج أفكار الديناميكا الحرارية ونظرية الكم مع النظرية العامة للنسبية ، مما يؤدي إلى ظهور مفاهيم جديدة غير متوقعة. الفكرة الأساسية هي أن الثقوب السوداء ليست مجرد أشياء هندسية. لديهم درجة حرارة ، لديهم انتروبيا هائلة ويمكن أن تظهر مظاهر التشابك الكمي. ستكون مناقشتنا للجوانب الديناميكية الحرارية والكمية لفيزياء الثقب الأسود أكثر سطحية وسطحية من تحليل ميزات الزمكان الهندسية البحتة في الثقوب السوداء المعروضة في الفصول السابقة. لكن هذه الجوانب ، وخاصة الكم ، هي جزء أساسي وحيوي من الدراسات النظرية المستمرة للثقوب السوداء ، وسنحاول جاهدين أن ننقل ، إن لم تكن تفاصيل معقدة ، روح هذه الأعمال على الأقل.

في النظرية العامة الكلاسيكية للنسبية - إذا كنا نتحدث عن الهندسة التفاضلية لحلول معادلات آينشتاين - فإن الثقوب السوداء سوداء حقًا بمعنى أنه لا يوجد شيء يمكن أن يخرج منها. أظهر ستيفن هوكينج أن هذا الموقف يتغير تمامًا عندما نأخذ في الاعتبار التأثيرات الكمومية: تتحول الثقوب السوداء إلى انبعاث إشعاعي لدرجة حرارة معينة ، تعرف باسم درجة حرارة هوكينج. بالنسبة إلى الثقوب السوداء ذات الحجم الفلكي الفيزيائي (أي من الثقوب السوداء للجماهير النجمية إلى الكتلة الفائقة) ، فإن درجة حرارة هوكينج لا تكاد تذكر بالمقارنة مع درجة حرارة خلفية الميكروويف الكونية - الإشعاع الذي يملأ الكون بأكمله ، والذي ، بالمناسبة ، يمكن اعتباره هو نفسه من أشكال إشعاع هوكينج. الحسابات التي أجراها هوكينج لتحديد درجة حرارة الثقوب السوداء هي جزء من برنامج بحثي أوسع في مجال يسمى الديناميكا الحرارية للثقوب السوداء. جزء كبير آخر من هذا البرنامج هو دراسة إنتروبيا الثقوب السوداء ، والتي تميز كمية المعلومات المفقودة داخل الثقب الأسود. الأجسام العادية (مثل قدح من الماء ، أو قضيب من المغنيسيوم النقي أو النجم) لها إنتروبيا أيضًا ، وأحد البيانات المركزية للديناميكا الحرارية للثقوب السوداء هو أن الثقب الأسود بهذا الحجم يحتوي على إنتروبيا أكثر من أي شكل آخر من المواد التي يمكن استيعابها في مساحة من نفس الحجم ، ولكن دون تشكيل ثقب أسود.

ولكن قبل أن نتعمق في مناقشة المشكلات المرتبطة بإشعاع هوكينج ونتروب الثقوب السوداء ، دعنا نأخذ رحلة سريعة إلى حقول ميكانيكا الكم ، الديناميكا الحرارية ، والتشابك. تم تطوير ميكانيكا الكم بشكل أساسي في عشرينيات القرن الماضي ، وكان هدفه الرئيسي هو وصف جزيئات صغيرة جدًا من المادة ، مثل الذرات. أدى تطور ميكانيكا الكم إلى تآكل مفاهيم الفيزياء الأساسية مثل الموضع الدقيق للجسيمات الفردية: اتضح ، على سبيل المثال ، أنه لا يمكن تحديد موقع الإلكترون عندما يتحرك حول نواة ذرية بدقة. بدلاً من ذلك ، تم تعيين ما يسمى بالمدارات للإلكترونات ، والتي لا يمكن تحديد مواقعها الفعلية إلا بالمعنى الاحتمالي. ولكن لأغراضنا ، من المهم عدم الانتقال إلى هذا الجانب الاحتمالي من المسألة بسرعة كبيرة. خذ أبسط مثال: ذرة الهيدروجين. يمكن أن يكون في حالة كمية معينة. إن أبسط حالة لذرة الهيدروجين ، التي تسمى الحالة الأرضية ، هي الحالة ذات الطاقة الأقل ، وهذه الطاقة معروفة على وجه التحديد. بمعنى أعم ، تسمح لنا ميكانيكا الكم (من حيث المبدأ) بمعرفة حالة أي نظام كمي بدقة تامة.

تأتي الاحتمالات إلى المشهد عندما نطرح نوعًا معينًا من الأسئلة حول نظام ميكانيكي الكم. على سبيل المثال ، إذا كان من المعروف أن ذرة الهيدروجين في حالة الأرض ، فقد نسأل: "أين الإلكترون؟" ووفقا لقوانين الكم
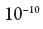
نحن نصل إلى هذا السؤال فقط تقديرًا معينًا للاحتمال ، تقريبًا شيء مثل: "من المحتمل أن يقع الإلكترون على مسافة تصل إلى نصف أنجستروم من نواة ذرة الهيدروجين" (أنجستروم واحد يساوي متر). لكن لدينا الفرصة ، من خلال عملية فيزيائية معينة ، للعثور على موضع الإلكترون بدقة أكبر بكثير من أنجستروم واحد. تتمثل هذه العملية ، الشائعة في الفيزياء ، في إطلاق فوتون مع طول موجي قصير للغاية في إلكترون (أو ، كما يقول الفيزيائيون ، نثر فوتون على إلكترون) - بعد ذلك يمكننا إعادة بناء موقع الإلكترون في لحظة الانتثار بدقة تساوي تقريبًا طول الموجة الفوتون. ولكن هذه العملية سوف تغير حالة الإلكترون ، بحيث بعد ذلك لن تكون في حالة الأرض من ذرة الهيدروجين ولن يكون لها طاقة محددة بدقة. ولكن لبعض الوقت ، سيتم تحديد موقعها تقريبًا تمامًا (دقيق إلى الطول الموجي للفوتون المستخدم في هذا). لا يمكن إجراء تقييم أولي لموضع الإلكترون إلا بالمعنى الاحتمالي بدقة تبلغ حوالي أنجستروم واحد ، ولكن بمجرد قياسه ، نعرف بالضبط ما الذي كان مساوياً له. باختصار ، إذا قمنا بقياس نظام ميكانيكي الكم بطريقة أو بأخرى ، ثم ، على الأقل بالمعنى المقبول عمومًا ، نمنحه "بالقوة" حالة ذات قيمة معينة للكمية التي نقيسها.

ميكانيكا الكم لا تنطبق فقط على الآليات الصغيرة ، ولكن (كما نعتقد) على جميع الأنظمة ، ولكن بالنسبة للأنظمة الكبيرة ، سرعان ما تصبح القواعد الميكانيكية الكم معقدة للغاية. المفهوم الرئيسي هو التشابك الكمومي ، مثال بسيط هو مفهوم الدوران (الدوران). للإلكترونات الفردية تدور ، لذلك في الممارسة العملية يمكن للإلكترون الواحد أن يدور موجها لأعلى أو لأسفل فيما يتعلق بالمحور المكاني المحدد. تدور الإلكترون هو كمية ملحوظة ، لأن الإلكترون يولد مجالًا مغناطيسيًا ضعيفًا ، يشبه مجال الشريط المغنطيسي. ثم تدور الإشارة إلى أن القطب الشمالي للإلكترون يشير لأسفل ، بينما تدور الإشارة إلى الأسفل تعني أن القطب الشمالي "يتطلع للأعلى". يمكن وضع إلكترونين في حالة كم مترافق ، حيث يكون أحدهما لديه تدور موجهًا للأعلى والآخر للأسفل ، لكن من المستحيل تحديد أي من الإلكترونات لديه أي دوران. في الواقع ، في الحالة الأرضية لذرة الهيليوم ، يوجد إلكترونان في مثل هذه الحالة تمامًا ، تسمى تدور - القميص ، حيث أن إجمالي الدوران لكلتا الإلكترونين يساوي الصفر. إذا انفصلنا عن هذين الإلكترونين دون تغيير دورانهما ، فيمكننا الاستمرار في الادعاء بأنهما يدوران معًا ، لكننا لا زلنا لا نستطيع تحديد ماهية تدور كل منهما على حدة. الآن ، إذا قمنا بقياس أحد دورانها ونثبت أنه موجه ، فسنكون متأكدين تمامًا من أن الثاني موجه. في هذه الحالة ، نقول أن ظهورهم متشابكة - ليس لأحدهم في حد ذاته معنى محدد ، في حين أنهم معًا في حالة كمية محددة.

كان آينشتاين قلقًا جدًا من ظاهرة التشابك: بدا أنه يهدد المبادئ الأساسية لنظرية النسبية. دعونا ننظر في حالة اثنين من الإلكترونات في حالة الدوران ، عندما تكون بعيدة عن بعضها البعض في الفضاء. من أجل الدقة ، دع أحدهم يأخذ أليس والآخر بوب. لنفترض أن أليس قامت بقياس دوران إلكترونها ووجدت أنه صاعد ، ولم يقيس بوب أي شيء. إلى أن أكملت أليس قياسها ، كان من المستحيل معرفة ماهية تدور الإلكترون الخاص به. ولكن بمجرد أن أكملت القياس ، كانت تعرف تمامًا أن لف إلكترون بوب يدور لأسفل (في الاتجاه المعاكس لتدوير الإلكترون الخاص بها). هل هذا يعني أن قياسها نقل على الفور إلكترون بوب إلى الولاية عندما يتم توجيه الدوران إلى الأسفل؟ كيف يمكن أن يحدث هذا إذا كانت الإلكترونات مفصولة مكانيا؟ شعر أينشتاين وزملاؤه في العمل ناثان روزن وبوريس بودولسكي أن قصة قياس الأنظمة المتشابكة كانت خطيرة لدرجة أنها تهدد وجود ميكانيكا الكم. تستخدم مفارقة آينشتاين - بودولسكي - روزن (EPR) التي صاغوها تجربة فكرية مماثلة لتلك التي وصفناها للتو لاستنتاج: ميكانيكا الكم لا يمكن أن تكون وصفا كاملا للواقع. الآن ، استنادًا إلى البحث النظري الذي تلا ، والعديد من القياسات ، تم إنشاء رأي مشترك مفاده أن مفارقة EPR تحتوي على خطأ ، ونظرية الكم صحيحة. التشابك الميكانيكي الكمومي حقيقي: قياسات الأنظمة المتشابكة سوف ترتبط ، حتى لو كانت هذه الأنظمة متباعدة في الزمان والمكان.

دعنا نعود إلى الموقف حيث وضعنا إلكترونين في حالة تدور ووزعناهما على أليس وبوب. ماذا يمكن أن نقول عن الإلكترونات قبل أخذ القياسات؟ أن كلاهما معا في حالة الكم معينة (تدور القميص). من المرجح أن يتم توجيه دوران الإلكترون Alicin لأعلى أو لأسفل. بتعبير أدق ، يمكن أن تكون الحالة الكمومية للإلكترون مع نفس الاحتمال واحدة (تدور) أو آخر (تدور لأسفل). الآن بالنسبة لنا مفهوم الاحتمال يأخذ معنى أعمق من ذي قبل. في السابق ، نظرنا في حالة كمية معينة (الحالة الأساسية لذرة الهيدروجين) ورأينا أن هناك بعض الأسئلة "غير المريحة" ، مثل "أين يقع الإلكترون؟" ، أسئلة لا توجد إجابات عنها إلا بالمعنى الاحتمالي. إذا طرحنا أسئلة "جيدة" ، على سبيل المثال: "ما هي طاقة هذا الإلكترون؟" ، فسنحصل على إجابات معينة عليها. الآن لا توجد أسئلة "جيدة" يمكن أن نسألها عن إلكترون أليس ، الإجابات التي لن تعتمد على إلكترون بوب. (نحن لا نتحدث عن أسئلة غبية مثل "هل تدور إلكترون أليس على الإطلاق؟" - أسئلة لا توجد إلا إجابة واحدة فقط عليها). وبالتالي ، سيتعين علينا استخدام لغة احتمالية لتحديد معالم أحد النظم غير المربكة. ينشأ اليقين فقط عندما ننظر في العلاقة بين الأسئلة التي يمكن أن يسألها أليس وبوب عن إلكتروناتهما.

لقد بدأنا عمداً بواحد من أبسط الأنظمة الكمومية الميكانيكية التي نعرفها: أنظمة الدوران للإلكترونات الفردية. ومن المأمول أن يتم بناء أجهزة الكمبيوتر الكمومية على أساس هذه النظم البسيطة. يُطلق على نظام الدوران للإلكترونات الفردية أو الأنظمة الكمومية المكافئة الأخرى الكيوبتيت (اختصار لـ "البتات الكمومية") ، والتي تشدد على دورها في أجهزة الكمبيوتر الكمومية ، على غرار الدور الذي تلعبه البتات العادية في أجهزة الكمبيوتر الرقمية.

تخيل الآن أننا استبدلنا كل إلكترون بنظام كم أكثر تعقيدًا بكثير ، وليس فقط حالتين كميتين. على سبيل المثال ، أعطوا أشرطة أليس وبوب من المغنيسيوم النقي. قبل أن يسلك Alice و Bob طريقهما المنفصلين في اتجاهات مختلفة ، يمكن أن تتفاعل أشرطةهما ، وسنتفق على ذلك من خلال اكتساب حالة كمية عامة معينة. بمجرد تباعد أليس وبوب ، تتوقف قضبان المغنيسيوم عن التفاعل. كما هو الحال في الإلكترونات ، يكون كل قضيب في حالة كمية غير محددة ، على الرغم من أنهما ، كما نعتقد ، يشكلان حالة محددة تمامًا. (في هذه المناقشة ، نفترض أن Alice و Bob قادران على تحريك قضبان المغنيسيوم دون إزعاج حالتهما الداخلية ، تمامًا كما افترضنا سابقًا أن Alice و Bob يمكنهما فصل إلكتروناتهما المتشابكة دون تغيير دورانهما). لكن الفرق بين هذه التجربة الفكرية والتجربة مع الإلكترونات هي أن عدم اليقين في الحالة الكمية لكل شريط كبير. قد يكتسب الشريط حالات كمية أكثر من عدد الذرات في الكون. هذا هو المكان الديناميكا الحرارية تدخل المرحلة. ومع ذلك ، يمكن أن يكون للأنظمة المعرّفة بشكل غير دقيق بعض الخصائص العيانية المحددة جيدًا. هذه الخاصية هي ، على سبيل المثال ، درجة الحرارة. درجة الحرارة هي مقياس للاحتمال الذي به أي جزء من النظام لديه متوسط ​​طاقة معين ، مع ارتفاع درجة الحرارة المقابلة لارتفاع احتمال وجود المزيد من الطاقة. المعلمة الديناميكية الحرارية الأخرى هي الانتروبيا ، والتي تساوي في الأساس لوغاريتم عدد الحالات التي يمكن للنظام أخذها. من الخصائص الديناميكية الحرارية الأخرى التي ستكون مهمة بالنسبة لشريط من المغنيسيوم مغنطيستها الكلية ، أي في جوهرها ، معلمة تُظهر كم من الإلكترونات يمكن أن تكون في الشريط مع أن تدور تشير إلى الأعلى أكثر من أن تدور تدور لأسفل.

لقد قمنا بإشراك الديناميكا الحرارية في قصتنا كوسيلة لوصف الأنظمة التي لا تعرف حالاتها الكمية بالضبط بسبب ارتباطها بالأنظمة الأخرى. الديناميكا الحرارية هي أداة قوية لتحليل مثل هذه الأنظمة ، لكن منشئيها لم يتوقعوا على الإطلاق مثل هذا التطبيق. كان كل من سعدي كارنو وجيمس جول ورودولف كلوسيوس قادة الثورة الصناعية في القرن التاسع عشر ، وكانوا مهتمين بمعظم الأسئلة العملية: كيف تعمل المحركات؟ الضغط والحجم ودرجة الحرارة والحرارة هي اللحم والدم للمحركات. وجدت كارنو أن الطاقة في شكل حرارة لا يمكن تحويلها بالكامل إلى عمل مفيد مثل رفع البضائع. دائما جزء من الطاقة يضيع. ساهم Clausius بشكل رئيسي في إنشاء فكرة الإنتروبي كأداة عالمية لتحديد فقد الطاقة أثناء أي عملية مرتبطة بالحرارة. كان انجازه الرئيسي هو إدراك أن الانتروبيا لا تنخفض أبدًا - في جميع العمليات تقريبًا. تسمى العمليات التي تزيد فيها الانتروبيا بأنها لا رجعة فيها - على وجه التحديد لأنها لا يمكن أن تنعكس بدون تقليل الانتروبيا. كانت الخطوة التالية في تطوير الميكانيكا الإحصائية هي كلوسيوس وماكسويل ولودفيغ بولتسمان (من بين أشياء أخرى كثيرة) - أظهروا أن الانتروبيا هي مقياس للاضطراب. عادةً ما تتصرف على شيء ما ، وكلما تعمدت الفوضى هناك. وحتى إذا كنت قد طورت عملية تهدف إلى استعادة النظام ، فستكون هناك قدر أكبر من الانتروبيا في سياقها أكثر مما سيتم تدميره ، على سبيل المثال ، عند إطلاق الحرارة. تخلق الرافعة ، التي تكدس الحزم الفولاذية بترتيب مثالي ، نظامًا من حيث موقع الحزم ، ولكن سيتم إطلاق قدر كبير من الحرارة أثناء تشغيلها ، بحيث لا تزال الإنتروبيا الكلية تنمو.

ومع ذلك ، فإن الفرق بين النظرة إلى الديناميكا الحرارية للفيزيائيين في القرن التاسع عشر والرأي المرتبط بالتشابك الكمومي ليس كبيراً كما يبدو. في كل مرة يتفاعل فيها النظام مع وكيل خارجي ، يتم خلط حالة الكم مع الحالة الكمية للعامل. عادة ما يؤدي هذا التشابك إلى زيادة عدم اليقين للحالة الكمومية للنظام ، وبعبارة أخرى ، إلى زيادة في عدد الحالات الكمومية التي يمكن أن يكون فيها النظام. نتيجة للتفاعل مع الأنظمة الأخرى ، ينمو عادة الانتروبيا ، المحدد من حيث مقدار الحالات الكمية المتاحة للنظام.

بشكل عام ، توفر ميكانيكا الكم طريقة جديدة لوصف النظم الفيزيائية التي تصبح فيها بعض المعلمات (مثل الوضع في الفضاء) غير مؤكدة ، في حين أن معلمات أخرى (مثل الطاقة) غالبًا ما تكون معروفة تمامًا. في حالة التشابك الكمي ، يوجد في جزأين منفصلين بشكل أساسي من النظام حالة كمومية معروفة ، وكل جزء على حدة هو حالة غير محددة. مثال معياري للتشابك هو زوج يدور في حالة قرد يستحيل فيه تحديد الدوران الموجه للأعلى والأسفل. , , , , .

, , , , . — , , , 2π. , , , ‑. , , , . : - ? , , , . , , 6 . , ( , ) . , 1,5 , . , , , , ; , , . , , . ( « , …», , , , .) , , : , , , , , , . , , , , , , , , . : ! , , , , , . , , , , , , . , -. , , - , .

, - , - . , , - : , . , , , , -, . , - , (, , , ). -, , , , , . - , . , 60 . , , ( ) ,



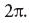
. 7.1. , a . , , t = 0. , t = 0 . , ‑.

, , « ». ? ? , . , , , . — , — , , . -, , ‑. - , , . , !

, , , — , , . «» , «», , , . 2, , , , . , , . , , ? , . , ? , , , . , , .