
مقدمة
هناك الكثير من المنشورات حول هبر التي تناقش مفهوم الانتروبيا ، وهنا فقط عدد قليل منها [1 ÷ 5]. وردت المنشورات بشكل إيجابي من قبل القراء وأثارت اهتماما كبيرا. يكفي إعطاء تعريف الإنتروبيا الذي قدمه مؤلف المنشور [1]: "الإنتروبيا هي مقدار المعلومات التي لا تعرفها عن النظام." كما أن المنشورات حول ظاهرة الفوضى في هبر كافية [6-9]. ومع ذلك ، لم يتم النظر في العلاقة بين الانتروبيا والفوضى في كلتا المجموعتين من المنشورات.
هذا يرجع إلى حقيقة أن مجالات المعرفة المختلفة تميز أنواع مختلفة من تدابير الفوضى:
- المعلومات؛
- الديناميكا الحرارية.
- التفاضلية.
- الثقافية.
كما يتم وصف تدابير الفوضى مع الأخذ في الاعتبار خصوصياتها ، حتى في واحدة من هذه المجالات أمر صعب للغاية.
في محاولة لتبسيط المهمة قدر الإمكان ، قررت النظر في العلاقة بين الإنتروبيا المعلوماتية والفوضى باستخدام مثال التشابه بين مناطق المرور من أجل الفوضى في الرسوم البيانية في شكل تعيينات نقطية وفي الرسوم البيانية لمعامل الانتروبيا لهذه المناطق.
ما جاء من هذا سوف تتعلم من خلال النظر تحت القط.
آليات الانتقال من أجل الفوضى
كشف تحليل لآليات الانتقال من النظام إلى الفوضى في النظم الحقيقية والنماذج المختلفة عن تعدد سيناريوهات الانتقال نسبيًا إلى الفوضى. يمكن تمثيل الانتقال إلى الفوضى في شكل مخطط التشعب (يستخدم مصطلح "التشعب" للدلالة على إعادة الترتيب النوعية للنظام مع ظهور طريقة جديدة لسلوكها).
يوصف دخول النظام في وضع غير متوقع من خلال سلسلة من التشعبات تلو الأخرى. يؤدي تسلسل التشعبات بالتسلسل إلى الاختيار بين حلين ، ثم أربعة وما إلى ذلك ، ويبدأ النظام في التذبذب في وضع مضطرب مضطرب يضاعف عدد القيم المحتملة بشكل متتابع.
ونحن نعتبر التشعب من فترة مضاعفة وظهور الفوضى في تعيينات نقطة. العرض هو وظيفة تُظهر اعتماد القيم التالية لمعلمات النظام على القيم السابقة:
xn+1=f(xn)= lambdaxn(1−xn)ضع في اعتبارك أيضًا الوظيفة الثانية شائعة الاستخدام:
xn+1=f(xn)= lambda cdotxn cdot(1−x2n)باستخدام تعيينات النقاط ، لا تتم دراسة الكائنات بشكل
مستمر ، ولكن مع وقت منفصل . عند الانتقال إلى الشاشة ، قد ينقص بعد النظام قيد الدراسة.
عند تغيير المعلمة الخارجية \ lambda ، تعرض تعيينات النقاط سلوكًا معقدًا إلى حد ما ، الأمر الذي يصبح فوضويًا مع \ lambda كبير بدرجة كافية. الفوضى هي ركود سريع للغاية من المسارات في الفضاء المرحلة.
التشعب هو إعادة هيكلة نوعية للصورة المتحركة. تسمى قيم معلمة التحكم التي تحدث فيها التشعبات القيم الحرجة أو قيم التشعب.
لإنشاء المخططات ، سنستخدم القائمتين التاليتين:
رقم 1. للحصول على الوظيفة:
xn+1=f(xn)= lambdaxn(1−xn)رقم 2. للحصول على وظيفة
xn+1=f(xn)= lambda cdotxn cdot(1−x2n)لتقييم تأثير طبيعة الوظيفة اللوجستية على القيم الحرجة
lambda النظر في الرسوم البيانية مع وظيفة
xn+1=f(xn)= lambdaxn(1−xn) للقيام بذلك ، سوف نستخدم القائمة رقم 1:
لـ 0 <\ lambda <1 لـ
lambda=0.95دولا و x0 = 0.47 نحصل على المخطط:
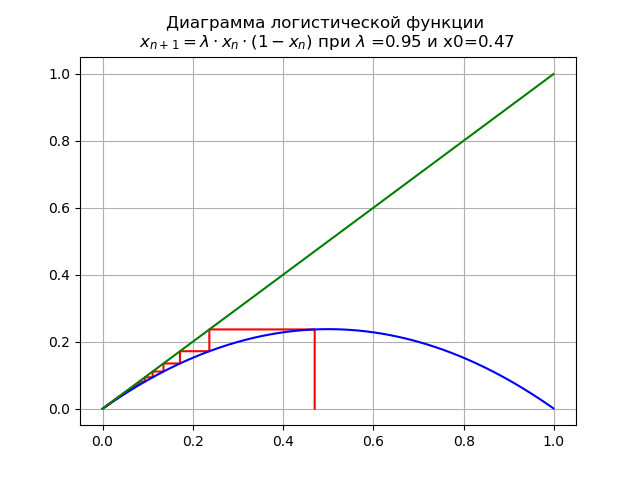
في هذه الحالة ، تحتوي الخريطة على نقطة ثابتة واحدة
x∗=0وهو مستدام.
في
1< lambda<3 إلى
lambda=2.5دولا x0 = 0.7 نحصل على المخطط:
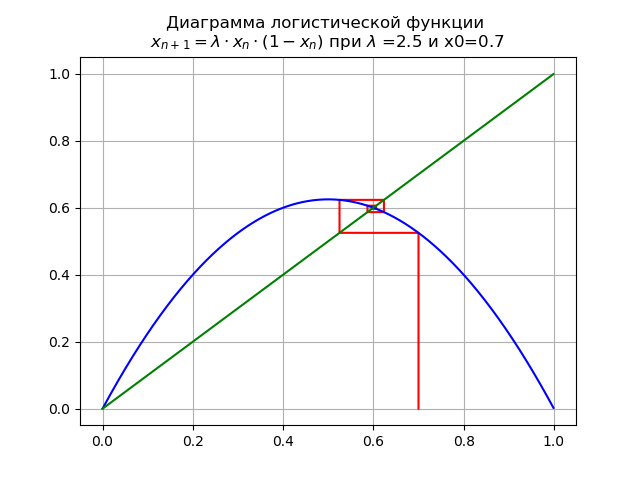
في المقطع [0 ، 1] ، تظهر نقطة ثابتة أخرى ثابتة
x∗1=1−1/ lambdaفي
1< lambda<3 إلى
lambda=2.5دولا و x0 = 0.01 نحصل على المخطط:
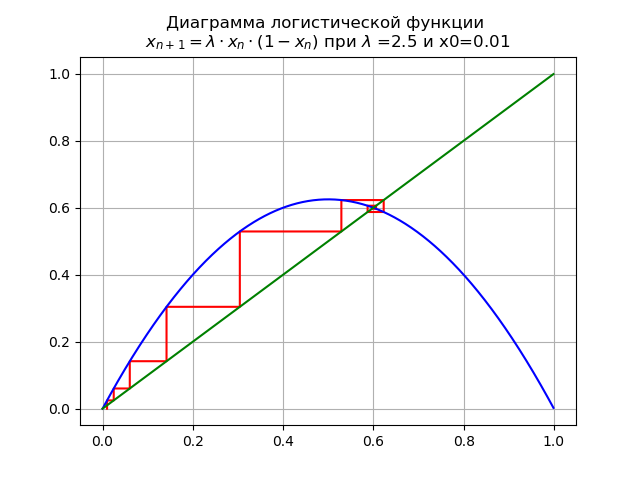
نقطة ثابتة
x∗=0 يفقد الاستقرار.
في
3< lambda<3.45 إلى
lambda=3.43دولا و x0 = 0.7 نحصل على المخطط:
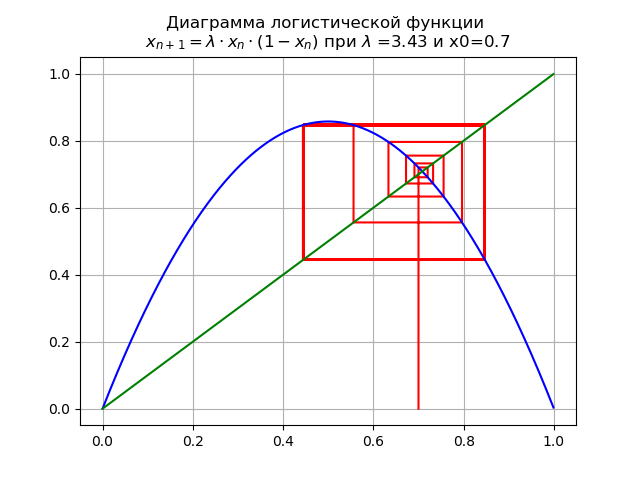
يخضع التعيين إلى تشعب: نقطة ثابتة
x∗1 تصبح غير مستقرة ، وتظهر دورة مزدوجة بدلاً من ذلك.
في

إلى
lambda=3.55دولاو x0 = 0.2 نحصل على المخطط:
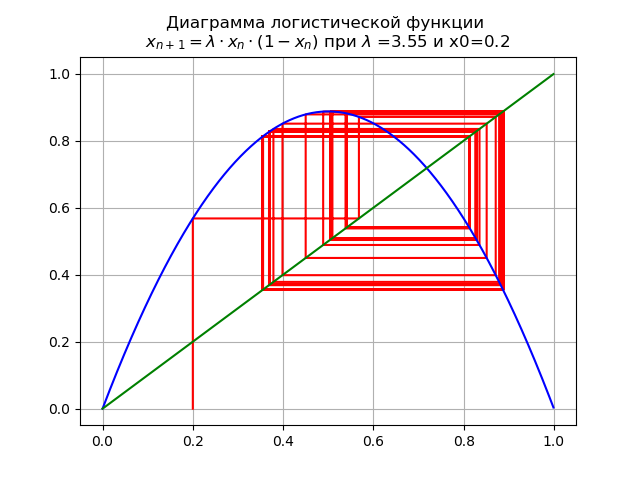
عند اجتياز المعلمة
lambda من خلال القيمة
lambda=3.45 ، وتصبح دورة 2 أضعاف 4 أضعاف ، وخارجها.
في القيمة النهائية
lambda=4 يحتوي النظام على دورات غير مستقرة لجميع الطلبات المحتملة:
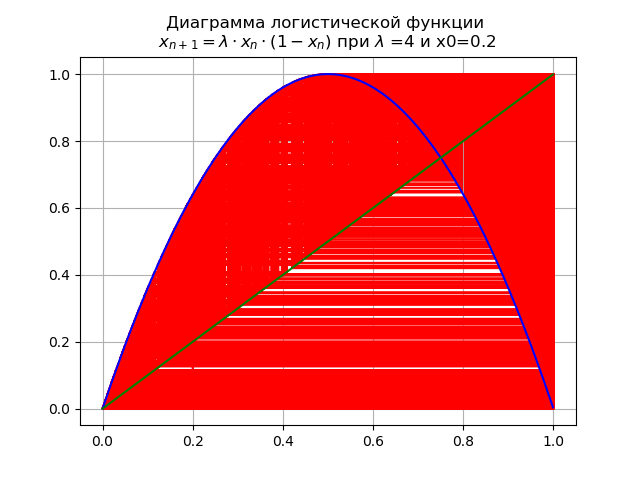
لتقييم تأثير طبيعة الوظيفة اللوجستية على القيم الحرجة
lambda النظر في الرسوم البيانية مع وظيفة
xn+1=f(xn)= lambda cdotxn cdot(1−x2n) ، لهذا سنستخدم القائمة رقم 2.
في
0< lambda<=1.0 إلى
lambda=0.5 و x0 = 0.2:

يحتوي التعيين على نقطة ثابتة واحدة
x∗=0 وهو مستدام.
في
1< lambda<=1.998... إلى
lambda=1.8دولا و x0 = 0.55:
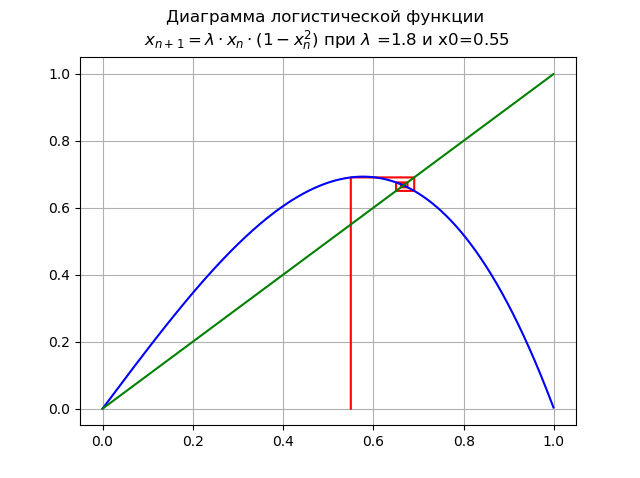
نقطة
x∗=0 يفقد الاستقرار ، تظهر نقطة مستقرة جديدة
x∗1في

إلى
لامدا=2.2دولا و x0 = 0.2:
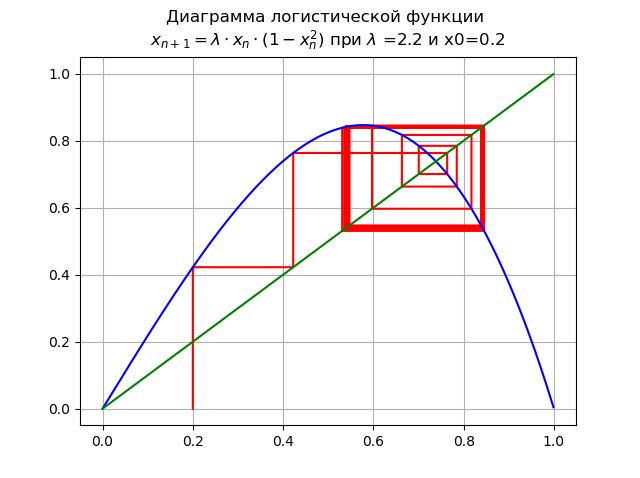
يحدث التشعب من مضاعفة الفترة ، تظهر دورة ذات شقين. زيادة أخرى
lambda يؤدي إلى سلسلة من فترة مضاعفة التشعبات.
في
2235< lambda2.5980... إلى
lambda=2.287 و x0 = 0.2:
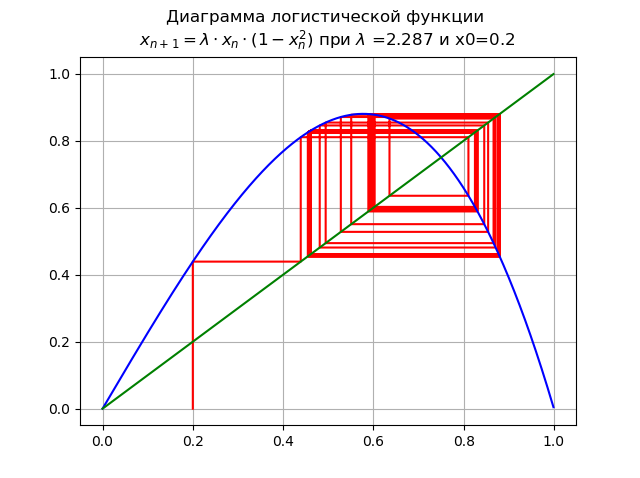
زيادة
lambda أدى إلى سلسلة من فترة مضاعفة التشعبات.
في
lambda=2.59 يحتوي النظام على دورات غير مستقرة لجميع الفترات المحتملة:
 كما هو مبين في الرسوم البيانية ، مع زيادة في ترتيب الوظيفة اللوجستية ، ومدى التغيير lambda التناقص التدريجي قبالة.
كما هو مبين في الرسوم البيانية ، مع زيادة في ترتيب الوظيفة اللوجستية ، ومدى التغيير lambda التناقص التدريجي قبالة.باستخدام الرسوم البيانية ، تتبعنا المسار من أجل الفوضى ، مع تحديد القيم
lambda لوظائف لوجستية مختلفة. يبقى أن نجيب على السؤال: كيف نقيس الفوضى؟ الجواب عن بعض أنواع الفوضى المدرجة في بداية المقال معروف
- الانتروبيا هو مقياس للفوضى. يمكن أن تعزى هذه الإجابة بشكل كامل إلى فوضى المعلومات ، ومع ذلك ، ما هو الانتروبيا المطبق هنا وكيف يمكن مقارنتها بالقيمة العددية التي تم النظر فيها بالفعل
lambda - سأحاول الإجابة على هذا السؤال في الجزء التالي من المقال.
انتروبيا المعلومات ومعامل الانتروبيا
سننظر في إنتروبيا المعلومات للأحداث العشوائية المستقلة.
x ج
ن الدول المحتملة موزعة مع الاحتمالات
pi(i=1،..،n) . يتم حساب إنتروبيا المعلومات الثنائية بواسطة المعادلة:
H(x)=− sumni=1pi cdotlog2(pi)وتسمى هذه القيمة أيضًا إنتروبيا متوسط الرسالة. قيمة
Hi=−log2(pi) دعا إنتروبيا الخاصة ، التي تميز فقط الدولة الأولى. في الحالة العامة ، يمكن أن تكون قاعدة اللوغاريتم في تعريف الانتروبيا أكبر من 1 ؛ يحدد اختياره وحدة قياس الانتروبيا.
سنستخدم اللوغاريتمات العشرية التي يتم فيها قياس الإنتروبيا والمعلومات بالبت. سيتم حساب كمية المعلومات بالبت بشكل صحيح عندما ، على سبيل المثال ، المتغيرات
X و
دلتا سيتم استبداله في التعبيرات المقابلة لـ entropy بغض النظر عن أيهما ، ولكن دائمًا في نفس الوحدات. في الواقع:
q=H(x)−H( Delta)=log10 left(X2−X1 right)−log10(2 Delta)=log10( fracX2−X12 Delta)حيث X و
دلتا يجب أن يكون في نفس الوحدات.
تم العثور على تقدير لقيمة الانتروبي لمتغير عشوائي من البيانات التجريبية من الرسم البياني من العلاقة التالية:
Deltae= frac12eH(x)= fracd2 prodmi=1( fracnni) fracnin= fracdn210− frac1n summi=1nilog10(ni)حيث:
د - عرض كل عمود في الرسم البياني ؛
مدولا - عدد الأعمدة ؛
ن كمية البيانات الإجمالية ؛
ni - كمية البيانات في
i هذا العمود.
يتم تحديد معامل الانتروبيا من النسبة:
ke= frac Deltae sigmaحيث:
سيجما - الانحراف المعياري.
انتروبيا المعلومات كمقياس للفوضى
لتحليل ظواهر فوضى المعلومات باستخدام معامل الانتروبيا ، نقوم أولاً بإنشاء مخطط فرعي لهذه الوظيفة
xn+1=f(xn)= lambdaxn(1−xn) مع تطبيق المناطق الانتقالية التي تم الحصول عليها أثناء بناء الرسم البياني:
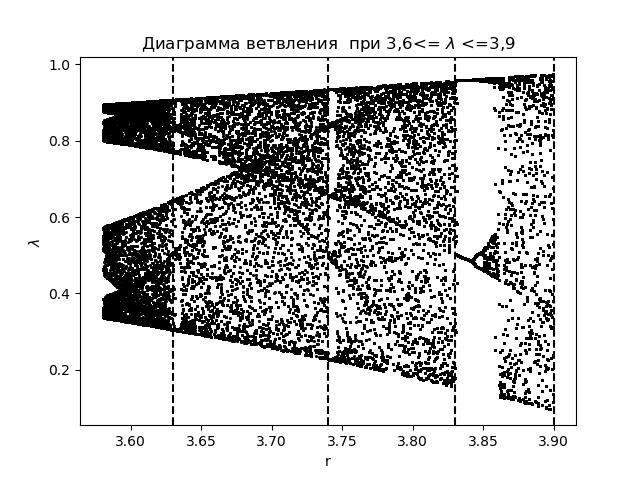
مخطط فرع import matplotlib.pyplot as plt import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(3.58,3.9,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-y[n-1]),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title(" 3,6<= $\lambda$ <=3,9") plt.xlabel("r") plt.ylabel("$\lambda$ ") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.show()
نحصل على:
نحن مؤامرة لمعامل الانتروبيا لنفس المناطق
lambda :
الرسم البياني لمعامل الانتروبيا import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(3.58,3.9,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-M[i-1,j]) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.title(" ke 3,6<= $\lambda$ <=3,9") plt.plot(arange(3.58,3.9,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.grid() plt.show()
نحصل على:

بمقارنة الرسم البياني والرسم البياني ، نرى عرضًا متطابقًا للمناطق على الرسم البياني وعلى الرسم البياني لمعامل الانتروبيا للدالة
xn+1=f(xn)= lambdaxn(1−xn) .
لمزيد من التحليل لظواهر فوضى المعلومات باستخدام معامل الانتروبيا ، نقوم بإنشاء مخطط فرعي للدالة اللوجستية:
xn+1=f(xn)= lambda cdotxn cdot(1−x2n) مع تطبيق المناطق الانتقالية:
مخطط فرع import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(2.25,2.56,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-(y[n-1])**2),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title(" 2.25<=$\lambda$ <=2.56") plt.xlabel("$\lambda$ ") plt.ylabel("y") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.show()
نحصل على:
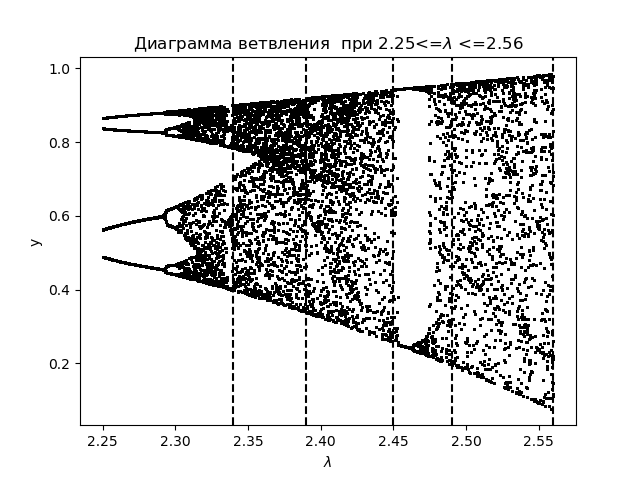
نحن مؤامرة لمعامل الانتروبيا لنفس المناطق
lambda :
الرسم البياني معامل الانتروبيا import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(2.25,2.56,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-(M[i-1,j])**2) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.figure(2) plt.title(" ke 2.25<= $\lambda$ <=2.56") plt.plot(arange(2.25,2.56,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.grid() plt.show()
نحصل على:
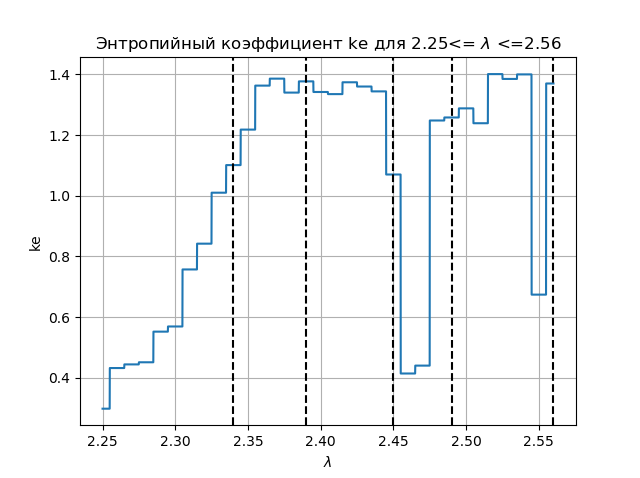
بمقارنة الرسم البياني والرسم البياني ، نرى عرضًا متطابقًا للمناطق على الرسم البياني وعلى الرسم البياني لمعامل الانتروبيا للدالة
xn+1=f(xn)= lambda cdotxn cdot(1−x2n)الاستنتاجات:
تم حل المشكلة التعليمية في المقال: هل الكون الإعلامي هو مقياس من الفوضى ، والإجابة على هذا السؤال تم التأكيد عليها من قبل بايثون.
مراجع
- الكون؟ إنه سهل!
- مقدمة لمفهوم الكون ووجوهه العديدة.
- الانتروبيا وأشجار القرار.
- أطروحة على الانتروبيا.
- الانتروبيا وينرر.
- النماذج الرياضية للفوضى.
- قليلا عن الفوضى وكيفية إنشائها.
- نظرة نقدية على جاذب لورنز.
- مولدات الفوضى FPGA.