في تقدير الانحدار الذاتي للكثافة الطيفية لإشارة ثابتة

أساليب التقدير الطيفي للعمليات العشوائية الثابتة القائمة على تحويل فورييه السريع (FFT) معروفة جيدًا وتستخدم على نطاق واسع في الممارسة الهندسية. تشمل عيوبها ، على وجه الخصوص ، تشتت عالية (دقة منخفضة) من التقدير مع فاصل مراقبة طويلة غير كافية لهذه العملية ، والتي عادة ما تظهر بصريا في رسم بياني قوي "المسافة البادئة" لكثافة الطيفية للقدرة (PSD). إحدى الطرق البديلة للتقدير الطيفي هي طريقة الانحدار الذاتي ، والتي تم بحثها في المثال أدناه ، وهو أقل شهرة في الممارسة الهندسية. في العديد من الحالات ، تجعل هذه الطريقة من السهل نسبياً الحصول على تقدير أفضل بكثير ل PSD (في الشكل 1) ، وأحيانًا حتى إلى معلومات أعمق حول العملية العشوائية قيد الدراسة.


الشكل 1: تقييم كلاسيكي و autocgressive من عملية PSD "قصيرة"

لأغراض العرض التوضيحي ، تم تصنيع إشارة زمنية منفصلة (تسلسل) x [i]. يتم تصميم الإشارة باستخدام نموذج ARMA (مرشح رقمي) يحاكي خصائص النظام الميكانيكي (1) - تحريك نقطة المادة x (t) في مذبذب "أحادي الكتلة" مع المعلمات m = 1 كجم ، c = 100 N / m ، k = 2 ، 5 كجم / ثانية ، وبسبب اضطراب في القوة - ضوضاء غوسية "بيضاء" (مع مراعاة التقدير التقديري) للضوضاء f (t) مع تشتت قدره 1 N ² ، الفاصل الزمني لأخذ العينات 0.1t = 0.12 ثانية.



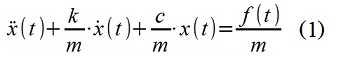
نموذج بنيت (2). لقد تم بالفعل النظر في طريقة بناء النموذج في وقت سابق هنا .

x [i] - 0.6388 · x [i-1] + 0.7408 · x [i-2] = 0.009667 · f [i-1] (2)

باستخدام (2) ، تم تجميع تسلسل من 50 ألف عينة ، والتي تم استخدامها من أجل مولد راندن متغير عشوائي موزعة عادة () من بيئة البرمجيات المعروفة.

بعد اكتمال محاكاة العملية x [i] ، يفترض أن المعلمات الكمية للنموذج (2) غير معروفة - فقط العملية نفسها ، وإلى حد ما ، تتوفر معلومات حول خصائص النموذج بعبارات عامة للبحث.

تم إجراء تقدير طيفي لتسلسل 50000 نقطة باستخدام طريقة ولش ، وتم أخذ حجم القطعة على قدم المساواة إلى 256 عينة ، وتم تطبيق نافذة هامينغ وتداخل 60 ٪ من القطاعات. يمكن تقدير الانحراف المعياري لمثل هذا التقدير ، استنادًا إلى حقيقة أن التسلسل يبلغ حوالي 200 مقطع غير متداخل ، تقريبًا 7٪ تقريبًا.

علاوة على ذلك ، على افتراض أنه في ظل ظروف حقيقية في التجربة ، يتوفر تسلسل أقصر بكثير للبحث ، وقد أجريت الدراسات فقط على أول 500 عينة من هذه الإشارة.

يتم الحصول على تقدير من خلال طريقة ولش مع نفس المعلمات. يبلغ الانحراف المعياري لمثل هذا التقدير 70٪ تقريبًا ؛ ويلاحظ وجود "قساوة" قوية للغاية للرسم البياني (الشكل 2).


الشكل 2. تقييم مديرية الأمن العام للعمليات "الطويلة" و "القصيرة" بالطريقة الكلاسيكية

استنادًا إلى حقيقة أننا نعرف الشكل التقريبي للدالة (الرسم البياني) لعملية SPM (على سبيل المثال ، استنادًا إلى الطبيعة المادية المعروفة للعملية - مذبذب أحادي الكتلة تحت ضوضاء بيضاء ، أو من تقييم عمليات مماثلة تتوفر لها تطبيقات أطول) باستخدام نموذج الانحدار التلقائي من الدرجة الثانية (AR (2) ، أو = ARMA (2.0)).

يعد تحديد ترتيب النموذج نقطة مهمة للغاية ؛ يمكن أن يؤدي الخطأ في الترتيب إلى أخطاء جسيمة جدًا في نتائج التقدير. هناك طرق لم يتم النظر فيها بعد ، مما يساعد في تحديد ترتيب النموذج بناءً على العملية التي يجري تحليلها فقط.

تم إجراء تقدير لمعلمات النموذج باستخدام معادلات Yule-Walker المعروفة لعملية الانحدار التلقائي (تم تعديلها قليلاً لتبسيط بنية البرنامج النصي قليلاً):



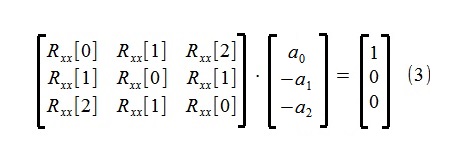
كما يتضح من المعادلات ، لتحديد المعلمات ، يتم استخدام الأعضاء الثلاثة الأوائل فقط من تسلسل الانحدار التلقائي Rxx [0] ، Rxx [1] ، Rxx [2] ، والتي تم تقديرها من التسلسل الأولي البالغ 500 نقطة × [i] بواسطة طريقة الارتباط ، ~ 4.5 ٪.

(بالمناسبة ، من الواضح أن "سلبيات" قبل ₁ ، a2 ₂ ، وما إلى ذلك ، غير مريحة للغاية. ظهرت بسبب الاستخدام "التنبئي" الغالب لنماذج ARMA في الاقتصاد ، في مصادرها "الهندسية" السابقة لا ، أنا أشك بالفعل في أنه كان من الضروري استخدام مثل هذا الفهم لمعاملات AR هنا.)

مصفوفة الارتباط في (3) في الممارسة العملية لها دائمًا انتشار قطري صارم | Rxx [0] | > | Rxx [i] | ، بما في ذلك بسبب وجود ضوضاء الملاحظة ، ونتيجة لذلك لا توجد صعوبات في التعامل معها (إيجاد حل (3)).

(لتوضيح مسألة حجم خطأ النمذجة الإحصائية ، من المثير للاهتمام أن نذكر ، على سبيل المثال ، تقدير Rxx [0] = 2.2606e-04 m ^{2 الذي} تم الحصول عليه من 500 عينة ، مقارنة بتقديرات التشتت التي تم الحصول عليها من 50000 عينة ، = 2.4238e-04 m ² والتقدير بواسطة integrand لمنطقة PSD التي تم الحصول عليها بواسطة طريقة ولش لـ 50000 عينة (الشكل 2) ، = 2.4232e-04 م ² )

بعد استبدال التقديرات التي تم العثور عليها Rxx [i] لدينا:



يتم تحديد معلمات النموذج التالية على ₀ = 11325.9 ؛ ₁ = 7090.1 ؛ a ₂ = -8411.5 ؛ كما يتضح من (3) ، تم تعيين تشتت الضوضاء البيضاء الواردة الافتراضية = 1 هنا ، وتحديد بدلاً منها الكسب a ₀ . يتم إنشاء تقدير الانحدار التلقائي لـ PSD بواسطة تحويل فورييه على سلسلة من المعاملات a ₀ ، a ₁ ، a ₂ :




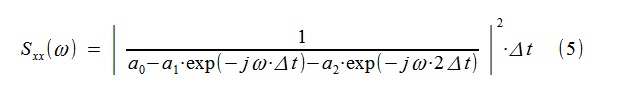
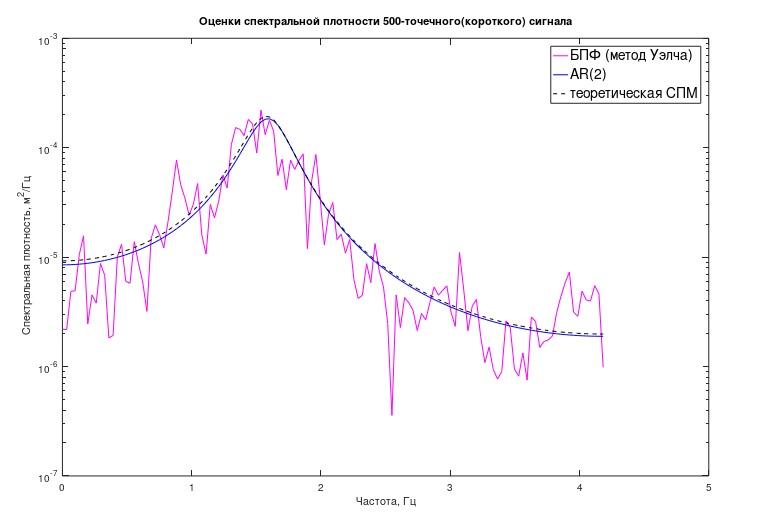الشكل 3: التقييم الكلاسيكي والانتقائي للشعبة PSD "القصيرة"

بالطريقة نفسها ، وفقًا لتعبير مشابه لـ (5) ، تم أيضًا إنشاء الجدول "النظري" لـ PSD سابقًا ، فقط معاملات النموذج هناك ، بالطبع ، تم أخذها مختلفة (من (2)).
يمكن أن يتبين من الرسم البياني أن تقدير AR الخاص بـ PSD قد أصبح قريبًا جدًا من المتوقع نظريًا. بالإضافة إلى الرسم البياني ، من الممكن محاولة تقييم بعض الخصائص التحليلية للعملية والنظام الميكانيكي المرتبط بها. في هذه الحالة ، هذه هي "أعمدة" النموذج ، والتي تميز عددياً ترددات قمم "الرنانة" للنموذج و "عوامل الجودة" المرتبطة به.

من (5) نجد العلاقة للبحث عن عدم التوافق لوظيفة النقل في نموذجنا باستخدام تحويل لابلاس (استبدال jω بـ λ = -ε + jω):



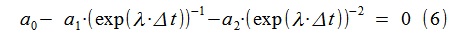
بالنسبة إلى نموذج AR الذي تم الحصول عليه ، تم حساب λ _1،2 = -1.5427 ± j · 10.1514 بهذه الطريقة ، وهي قريبة جدًا من النموذج الأصلي المستخدم لإنشاء العملية
_{t 1.2theor} = -1.2500 ± j · 9.9216 (على سبيل المثال ، مواقع ذروة الرنين ، على التوالي ، 1.615 هرتز (نظريًا) و 1.579 هرتز (محددًا)).


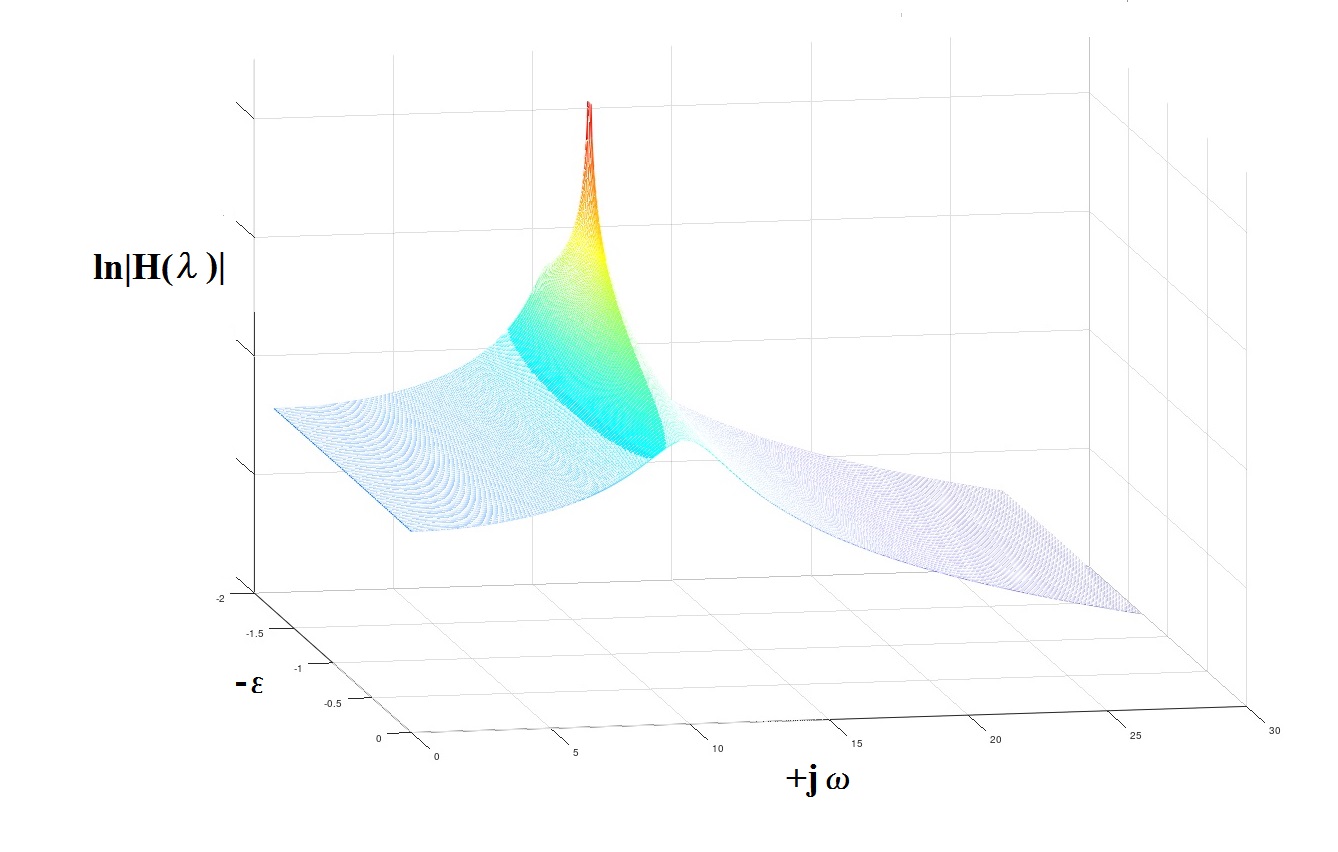الشكل 4 حول مفهوم "القطبين"

بعض التعليقات والتوصيات في الختام.

1. عادةً ما يكون الترتيب "المفرط" (الكبير جدًا) لنموذج AR أقل خطورة من كونه غير كافٍ ، من وجهة نظر خطر الحصول على تقدير PSD مع وجود أخطاء جسيمة.
2. كقاعدة عامة ، نمذجة AR تجعل من الممكن تحديد بدقة ترددات الرنين jω _k بدقة وبدرجة أقل بكثير تحديد عرض "قمم" المقابلة -ε _k
3. ARMA - يمكن أن يتحول النموذج إلى حجم (حجم) أصغر من نموذج AR ، والذي يبدو أنه يهدف إلى تحسين دقة النموذج ، وفقًا للعديد من المصادر. ومع ذلك ، فإن تقييم الجزء MA من النموذج أكثر صعوبة وقد يشمل عمومًا الخطوة الأولى في الحصول على نموذج AR كبير الترتيب من أجل تحويله إلى جزء MA. فيما يتعلق بهذه المصادر ، يتم التعبير عن رأي بديل أيضًا حول مدى استصواب استخدام نماذج AR بالضبط لتقدير الطيف ، وإن كان بترتيب أعلى.
4. لفترة قصيرة جدًا ، وكذلك للعمليات غير الثابتة ، بدلاً من مصفوفة تقديرات دالة الارتباط التلقائي ، عادةً ما يتم استخدام مصفوفة التغاير في (3).
5. لدراسة مفصلة لقضية التقدير الطيفي الانحداري ، S.L. ماربل مل. "التحليل الطيفي الرقمي وتطبيقاته" ، M. ، مير ، 1990