عن قرب القمم

"قبل أن تفهم هذا ، يبدو وكأنه معجزة. ولكن بعد ذلك لا يوجد شيء خاص ".

لا ، ليس عن الجبال ، - عن التهم الموجهة إليه. في الرياضيات ، هناك أسئلة يستطيع الجميع الوصول إلى صياغتها ، ولكن الحل غير تافه وبدون إعداد خاص يصعب شرحه. واحدة من هذه المشاكل يمكن التعبير عنها لفترة وجيزة على النحو التالي: كيفية حساب المسافات في الرسوم البيانية الموجهة بشكل صحيح؟ يمكن تقليل هذه المشكلة المجردة إلى حد ما إلى مهمة تحفيزية محددة للغاية. تناسبها في صورة واحدة:

1. بيان المشكلة. أنا أعيش على واحد ، ولكن أنت من جهة أخرى.

تقسم البلدة الصغيرة (على سبيل المثال ، بواسطة نهر ، على الرغم من أنه في سياق القمم يكون الخانق أكثر ملاءمة) إلى منطقتين (أجزاء) $$$دولا$ و $$$B$ . يتم التواصل بين المقاطعات على طول طريق واحد (جسر) ، به طريقان: إلى جانب $$$دولا$ إلى $$$B$ والعكس صحيح. فيما يتعلق بالنمو السكاني ، نشأ السؤال حول زيادة قدرة الطريق. المال كالمعتاد بالكاد ويكفي فقط لممر واحد في اتجاه واحد. من الواضح أنه حتى حارة واحدة سوف تقرب المناطق من بعضها البعض ، لكن السؤال هو كم بالضبط؟ أنت عالم رياضيات مدني مجنون ، وقد تمت دعوتك لتلقي إجابة معقولة .

ما مدى قرب المناطق إذا قمت ببناء شريط آخر في اتجاه واحد؟

صيغة متقدمة

بدلاً من جسور Konigsberg ، يمكن استخدام لغة نظرية بيانية أكثر صرامة. لذلك ، هناك رسم بياني موجه مع رأسين (العقد) $$$دولا$ و $$$B$ . حجم الاتصال (الموصلية ، عرض النطاق الترددي) في الاتجاه الأمامي والخلفي متساويان في البداية. والسؤال هو كم ستتغير المسافة بين العقد إذا تضاعفت الموصلية في أحد الاتجاهات؟

ونعم ، إذا كنت تعمل في عالم رياضيات حقيقي ، فيمكنك تقديم (وتبرير) حل لأي قيم مباشرة وتعليقات. من الناحية المثالية ، للرسم البياني مع أي عدد من العقد والروابط.

الحميمية والتجول في حالة سكر

من الواضح أن المسافة (كيلومترات) المعتادة بين المناطق لا تعتمد على وجود أو عدم وجود الطريق. لذلك ، لا يصلح هنا - نحن بحاجة إلى الاعتماد على الاتصالات. كلما زاد اتصال المناطق - كلما كانت أقرب - كلما زاد عدد السكان الذين يمكنهم الوصول إلى منطقة أخرى لكل وحدة زمنية.

لتقييم قياس القرب بين العقد من رسم بياني غير موجه ، يمكن استخدام ما يسمى المسافة المقاومة . في وقت سابق ، وصفنا بالفعل خصائص هذه المسافة على habr في العديد من المقالات .

المسافة المقاومة تعادل مفهوم المقاومة الفعالة ، عندما يتعلق الأمر بالشبكة الكهربائية. لذلك ، في اللغة الكهربائية ، يمكن صياغة المشكلة على النحو التالي. بين العقدتين ، ترتبط اثنين من الثنائيات من الموصلية متساوية عكس اتجاه عقارب الساعة. كيف ستتغير المقاومة بين هذه النقاط إذا قمت بإضافة صمام ثنائي آخر؟ (أعتذر إذا فشلت اللغة الكهربائية وكتبت هراء هنا).

أيضا ، يمكن تفسير المقاومة الفعالة في لغة ماركوف لاحتمالات المشي العشوائي في حالة سكر (لأولئك الذين يرغبون في الخوض في الموضوع - جوجل "مناحي عشوائية والشبكات الكهربائية").

المسافة المقاومة من الدرجة الثانية ، - تتوافق مع مربع المسافة الخطية. وتسمى المسافات التربيعية أيضًا quadrans . ولكن نظرًا لعدم استخدام مسافات (خطية) أخرى في هذه المشكلة ، فنحن لسنا بحاجة إلى مصطلح quadrans هنا. (هناك لسان كافٍ للطير حتى بدونه).

بشكل عام ، فإن مصطلح "المسافة المقاومة" لا يبدو جيدًا أيضًا. إنه يعني أننا نتحدث عن نوع من المسافات غير المعتادة التي لا يعرفها العلم. في الواقع ، فإن المسافة المقاومة هي المسافة الإقليدية المعتادة. ولكن في الفضاء أفيني. نحن نستخدم هذه الميزة منه كذلك.

وما هي في الواقع المشكلة؟

إذا علمنا ما هي "المسافة المقاومة" ، فلماذا لا يمكننا "أخذها وحسابها" فقط للرسم البياني المحدد؟

هم. من حيث المبدأ ، سهل. إذا كنا نتحدث عن رسم بياني غير موجه. إذا كانت المدينة قد بنيت شرائط في كلا الاتجاهين ، فإن المسافة المقاومة ستنخفض بمقدار النصف بالضبط. لأن المقاومة تتناسب عكسيا مع الموصلية ، وقد تضاعفت الموصلية (الإنتاجية). وإذا أضفت نطاقين في كل اتجاه ، فسوف تقل المسافة بمقدار 3 مرات. كل شيء تافه جدا هنا. (وربما شخص ما هنا يمكنه بالفعل تخمين الشكل العام للحل. ونذهب إلى أبعد من ذلك).

عندما تكون العلاقات المعارضة غير متساوية ، يصبح كل شيء معقدًا. وبشدة شديدة.

لا توجد طريقة قانونية مقبولة بشكل عام لتحديد مدى قرب القمم (المسافات المقاومة) في الرسم البياني الاتجاهي .

(هذه هي أطروحتي - ربما يمكن لأي شخص أن يقنعني). "لا" - هنا يعني أنها ليست في الكتب المدرسية ، ويكي ، وفي الرؤوس (وبشكل أكثر دقة - هناك العديد من الطرق المختلفة من مؤلفين مختلفين تتطلب افتراضات وتعريفات مختلفة). هناك طريقة (وإن لم تكن بهذه البساطة). في هذه المقالة ، نحن فقط تصف ذلك.

يتطلب تحديد المسافة في وجود اتصالات موجهة توضيحًا إذا كنا نتحدث عن رسم بياني موجه (قياس غير تبادلي ، أعتذر). يمكنك التحدث عن المسافة من $$$دولا$ إلى $$$B$ ولكن يمكنك ذلك $$$B$ إلى $$$دولا$ . والأرجح أن هذه المسافات ليست متساوية دائمًا. ما نوع المسافات التي نتحدث عنها في المشكلة؟

قواعد المسافة الإقليدية

سوف نخرج ونأخذ نفسا عميقا. لقد ذكرنا بالفعل أن المسافة المقاومة هي الإقليدية المعتادة. وهذا يعني أن تعريفه يمكن اختزاله إلى تعريف المسافة الإقليدية كمعيار للفرق بين عنصرين:

$$$S (A، B) = | A - B | ^ 2 = (A - B) ^ 2 = (A - B) \ cdot (A - B) = S (B، A) \ quad (1)$

هذا التعريف لا يعتمد على ترتيب العناصر - هذه هي المسافة التبادلية ، القرب (بدقة أكثر ، المسافة) للعناصر. تعني نقطة في تعبير عملية منتج عددي (مساحة مترية). وفقًا لذلك ، يمكن الكشف عن التعبير (1):

$$$S (A، B) = S (B، A) = A ^ 2 + B ^ 2 - A \ cdot B - B \ cdot A \ quad (2)$

هنا $$$A ^ 2 = A \ cdot A$ . $$$B ^ 2 = B \ cdot B$ - قواعد العناصر. عندما يتعلق الأمر بالرسوم البيانية ، فإن معايير العناصر تكون عادة صفرية. في المشكلة الأصلية ، لا يُقال شيئ عن المعايير ، بحيث يمكنك اعتبارها صفرية (مزيد من المعلومات حول ما تعنيه معايير العناصر في الفضاء الخاص. هنا ، وحتى مزيد من التفاصيل ، هنا ). ثم يأخذ التعبير عن المسافة المطلوبة النموذج:

$$$S (A، B) = - (A \ cdot B + B \ cdot A) = s_ {AB} + s_ {BA} \ quad (3)$

وفقًا للتعبير (3) ، كل ما هو مطلوب لحل المشكلة هو العثور على المنتجات العددية للعناصر (العقد) في رسم بياني موجه (من السهل القول ، ولكن كيف نفعل ذلك؟).

على طول الطريق ، تظهر الصيغة (3) أن مقياسنا العام (التبادلي) للقرب من العناصر $$$دولا$ و $$$B$ هو مجموع مسافتين موجهتين:

$$$s_ {AB} = - A \ cdot B$ - المسافة الاتجاه من $$$دولا$ إلى $$$B$ .
$$$s_ {BA} = - B \ cdot A$ - المسافة الاتجاه من $$$B$ إلى $$$دولا$ .

2. القرار. طريق طويل في الكثبان الرملية

هدأت الدمدمة. المرح قد انتهى. ثم تأتي التفاصيل المملة لوصف جوهر الطريقة لحساب المنتج القياسي بين العقد من الرسم البياني الموجه. هذا هو الجزء الذي لا أعرف كيف أقوله "بطريقة بسيطة على الأصابع". ولكن هذا هو المكان الأكثر أهمية في المقال. شيء يستحق إضاعة الوقت في ذلك.

الخط العام للتفكير هو على النحو التالي. نقوم بعناية وبدون عواطف بافتراضات إضافية جديدة بنقل الخصائص المعروفة لمقياس المسافات المتماثلة إلى تلك غير المتماثلة. كل ما نحتاجه هو أن نأخذ في الاعتبار خصوصيات المقياس في المساحات الأفقية.

يحدد أي رسم بياني متصل (سواء كان موجها أم لا) مساحة متري أفيني. تم وصف بعض خصائص هذه المساحات في التنفيذ المتناظر (التبادلي) في سلسلة المقالات المذكورة بالفعل أو بشكل أكثر تفصيلًا وبالتفصيل في longrid المذكور. لا تتعجل للتبديل - أدناه نعطي (على الرغم من الإعصار اللسان) العصرات الرئيسية.

مساحة مترجم أفيني (رسم بياني غير موجه)

ما هو المهم معروفة أولا.

1. تقارب الفضاء يعني أن مفهومي المتجهات والعنصر في الفضاء مختلفان. المتجه هو اختلاف العناصر. تؤدي هذه الميزة التي تبدو غير مهمة إلى عواقب كبيرة إذا تم تحديد مقياس في الفضاء.

2. يتم تعريف الفضاء على أساس يتكون من العناصر. قمم الرسم البياني هي أساس الفضاء. تحدد العلاقات في الرسم البياني خصائصه المترية.

3. خاصية ربط الرسم البياني هي المصفوفة المجاورة . لكن بالنسبة للخصائص المترية (وغيرها) ، فإن اللابلاشيان للرسم البياني (مصفوفة كيرشوف) أكثر أهمية $$$L$ .

4. Laplacian من الرسم البياني هو الموتر تقريبا متري. "تقريبا" - هنا يعني أنها غير مكتملة. Laplacian هو مصفوفة انحطاط وبالتالي لا يمكن عكسها. و tensor متري قياسي هو عكسها تماما.

الآن أقل شهرة.

5. يؤدي الاختلاف بين العناصر والمتجهات في مساحة متري أفيري إلى وجود متجه فارغ فيه $$$\ mathbb z$ . ناتج العددية للعناصر ذات المتجه الفارغ في مساحة تبادلية (متناظرة) يساوي الوحدة (في الفضاء غير التبادلي يعتمد على اتجاه الضرب). بدون متجه صفر ، مساحة الرسم البياني غير كاملة! هذا مهم.

6. المركز المتعامد للأساس مزدوج فيما يتعلق بالمتجه الفارغ. $$$Z$ . هذا عنصر من العناصر المتعامدة لجميع العناصر الأخرى في الأساس (باستثناء الموجه الصفري). تذكر أن تعامد العناصر يعني أن منتجها القياسي هو صفر. orthocenter للمثلث هو دائرة مقيدة . نعم ، في الفضاء الضيق الكامل ، لا يعد العنصر ذو القاعدة غير الصفرية نقطة بل مجال كروي.

7. يصبح Laplacian من الرسم البياني ، مع إحداثيات مركز المتعامد ، كاملة (موتر متري كامل). وبعبارة أخرى ، كامل اللابلية $$$Lm$ هو عدد العادي laplacian $$$L$ ولكن يحدها إحداثيات مركزية من مركز متعامد.

8. انقلاب كامل Laplacian يسمح واحد للحصول على غرامى كاملة $$$ج$ - مصفوفة المنتجات العددية لعناصر الأساس (في حالتنا ، رؤوس الرسم البياني). هذا gramian هو أيضا tensor متري كامل من الفضاء.

9. إن تأطير الحبيبة الكاملة عبارة عن مجموعة من الوحدات (المنتجات العددية للعناصر الأساسية ومتجه صفري). في الزاوية - صفر ، هذا هو المعيار الخاص بموجه الصفر نفسه.
مصفوفة كاي-مينجر الشهيرة عبارة عن غرامى منتظم.

نتيجة لذلك ، نستنتج أنه وفقًا للادعاء 8 ، فإن مشكلة تحديد المنتجات العددية (وبالتالي المسافات) بين العقد في الرسم البياني تقل إلى تحديد الموتر المتري الأولي للأساس $$$ج$ .

نحتاج إلى طريقة لإنشاء رسم بياني كامل $$$ج$ للحصول على (غير كاملة) Laplacian $$$L$ .

في حالة الروابط المتناظرة ، لا يتسبب إنشاء غرامي كامل من اللابلاسية (والعكس) في أي صعوبات معينة. في هذه الحالة ، تكون المنتجات العددية لعناصر الأساس والناقل الصفري تبادلية - فهي لا تعتمد على ترتيب الضرب:

$$$\ mathbb z \ cdot A = A \ cdot \ mathbb z = 1$

بالنسبة إلى الرسوم البيانية الموجهة (المساحات غير التبادلية) ، تكون المشكلة معقدة. إذا فقط لأن عدد الاتصالات الممكنة في الرسم البياني الموجه يتضاعف.

مساحة أفين غير تبديلية (الرسم البياني الموجه)

حول خصائص Laplacian من الرسم البياني الموجه ، كما كتبنا بالفعل على هبر . قالوا لك كيفية استخدام إمكانيات Laplacian لتصنيف الكائنات. من حيث القواعد ، فإن إمكانيات Laplacian هي الإحداثيات المزدوجة لمتجه الصفر (مبيد لل Laplacian).

في هذه المقالة ، نحن مهتمون بالخصائص المترية. إذا تم توجيه الرسم البياني ، فإن المنتج القياسي بين رؤوسه يعتمد على الترتيب:

$$$A \ cdot B \ ne B \ cdot A$

هذا يعني أن الإحداثيات المزدوجة في الرسوم البيانية الموجهة يتم تقسيمها (إلى اليسار واليمين). تعتمد قيم المنتجات العددية للناقلات الصفرية وعناصر الأساس (المتاخمة للغرامي) أيضًا على ترتيب العوامل. وبالتالي ، على عكس المساحة التبادلية ، هنا نصف الإحداثيات المزدوجة للموجه الصفر غير معروف ويجب تحديده.

$$$\ mathbb z \ cdot A \ ne A \ cdot \ mathbb z$

ومع ذلك ، هناك العديد من الكميات المعروفة.

أولاً ، اللابلاسيان نفسه معروف. بالإضافة إلى ذلك ، من المعروف أن مجموع صفوفه هو صفر (في الحالة العامة ، يعد هذا مطلبًا اختياريًا ، ولكن بالنسبة إلى Laplacians من الرسوم البيانية الموجهة ، تكون هذه هي الحالة عادةً). من المهم أيضًا أن تكون إحداثيات مركزية العناصر فريدة من نوعها ، لأنها مستقلة عن قياس المسافة. بمعنى أن حدود اللابلاسيان في الرسم البياني متناظرة لكل من الرسم البياني الموجه وغير الموجه (لم أتعرف على الفور على هذه النقطة). أخيرًا ، نحن نعرف معايير عناصر الأساس (عادةً ما تكون في الرسوم البيانية مساوية للصفر).

يبقى استبدال كل المجهول والمجهول في الهوية التي تربط اللابلاشي والجراميان:

$$$Lm \ Gm = I$

هنا $$$I$ هي مصفوفة الهوية. في هذه الهوية ، معنى الانتقال من Laplacian غير مكتمل إلى واحد كامل.

اخرس ونعتقد

دعنا ننتقل من الأقوال إلى الأفعال. هذا ما يبدو عليه اللابلاسيون $$$L$ للحصول على رسم بياني للعقدتين:

$$$L = \ تبدأ {bmatrix} c_1 & -c_1 \\ c_2 & -c_2 \ end {bmatrix}$

للبساطة ، لقد حددنا العلاقة مع الأرقام: $$$c_1 = c_ {AB} ، c_2 = c_ {BA}$ . من المفترض أن تكون قيم السندات معروفة - من خلالها سنعبّر عن جميع الكميات الأخرى.

لابلاسيان كامل $$$Lm$ يتضمن إحداثيات orthocenter $$$[rz، az، bz]$ :

$$$Lm = \ تبدأ {bmatrix} rz & az & bz \\ az & c_1 & -c_1 \\ bz & c_2 & -c_2 \ end {bmatrix}$

هنا $$$rz$ - قاعدة orthocenter (في الحالة المتماثلة يتم تفسيرها على أنها مربع نصف القطر) ، $$$az$ و $$$bz$ - معاملات تحلل orthocenter على أساس $$$A ، B$ (أوزان متحدة المركز).

غرامى كامل $$$ج$ يبدو شيء مثل هذا:

$$$Gm = \ start {bmatrix} 0 & za & zb \\ 1 & 0 & g_1 \\ 1 & g_2 & 0 \ end {bmatrix}$

هنا هم tuples $$$[za، zb]$ و $$$[1 ، 1]$ تعكس الإحداثيات المزدوجة للمتجه الخالي. هذه الإحداثيات هي إبادة للابلاشيان (عند ضرب اللابلاسيون فإنها تعطي متجهًا صفرًا - لا يجب الخلط بينها وبين متجه الصفر!).

لحل المشكلة ، نحتاج إلى إيجاد مجموع قيم gramian: $$$- (g_1 + g_2)$ .

نحن نعتبر عدد المجهولين: $$$rz ، az ، bz ، za ، zb ، g_1 ، g_2$ - فقط 7 (نعم ، نعم - لمعرفة قيمة مسافة مؤسفة واحدة ، نحتاج إلى حساب سبع قيم إضافية). هناك اتصالان معروفان عند المدخل - $$$c_1$ و $$$c_2 دولا$ . هوية $$$Lm \ Gm = I$ سوف تعطي 9 معادلات. المجموع 7 + 2 = 9 ، - كل شيء يتقارب (بشكل مدهش). يبقى ببساطة حل نظام المعادلات.

للحصول على رسم بياني للعقدتين ، يمكن التعبير عن الحل (جميع العناصر المجهولة) في شكل واضح. نعطي تعبيرات محدودة للكميات التي تهمنا. نقدم مفهوم الاتصال الهندسي العام - وهذا هو مبدأ متبادل لقاعدة المركز المتعامد $$$gc = 1 / rz$ . بعده يتزامن مع البعد من الروابط الرسم البياني. للحصول على رسم بياني للعقدتين (واثنين من الاتصالات) ، يكون للتوصيل الهندسي تعبير لطيف:

$$$gc = 1 / rz = (\ sqrt {c_1} + \ sqrt {c_2}) ^ 2$

من خلال هذا الصدد ، يمكن للمرء التعبير عن المنتجات العددية للعقد:

$$$g_1 = -gc \ sqrt {c_2} ، \ quad g_2 = -gc \ sqrt {c_1}$

يمكنك ترجمة المنتجات العددية $$$g$ في المسافات الاتجاهية $$$s$ (3):

$$$s_ {BA} = gc \ sqrt {c_ {AB}} ؛ \ quad s_ {BA} = gc \ sqrt {c_ {AB}}$

يتم تحديد المسافة التبادلية المرغوبة بين العقد بالمجموع:

$$$S (A، B) = s_ {BA} + s_ {AB} = 1 / \ sqrt {c_ {AB} c_ {BA}} \ quad (4)$

وصلت الجدة

وأخيرا. التعبير (4) - هذه هي الصيغة المطلوبة.

المسافة بين رؤوس الرسم البياني للعقدتين تتناسب عكسيا مع الجذر التربيعي لمنتج الوصلات المضادة.

يمكنك تحميل الكتاب المدرسي مع صيغة أخرى عديمة الفائدة.

إذا كانت الاتصالات متساوية ، فإن النتيجة تتزامن مع المسافة المقاومة في الرسوم البيانية غير الموجهة:

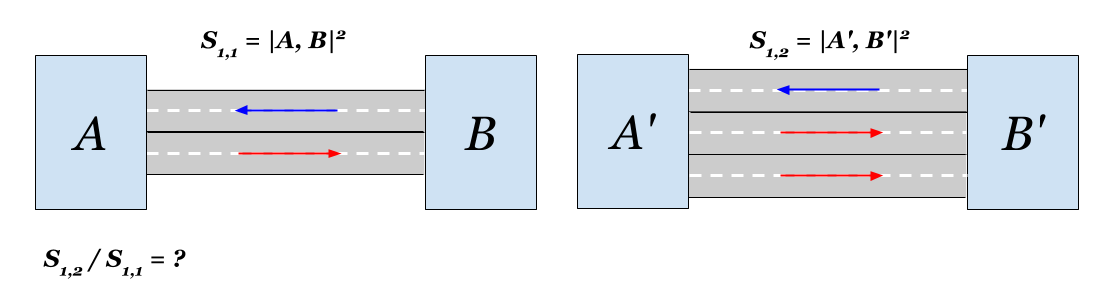
$$$S_ {c، c} (A، B) = 1 / c \ quad (4.1)$

سوف نحسب ما هو هناك مع مدينتنا. إذا وضعت حارة ثانية ، فسوف يتضاعف التواصل في اتجاه واحد. تبعا لذلك ، المسافة الجديدة $$$S_ {1، 2} (A، B)$ يمكن التعبير عنها من حيث الأصل:

$$$S_ {1، 2} (A، B) = 1 / \ sqrt {2 c_ {AB} c_ {BA}} = 1 / \ sqrt {2} S_ {1، 1} (A، B)$

ستنخفض المسافة بين المناطق $$$\ sqrt {2}$ الوقت. كان واضحا ، أليس كذلك؟

كما تبين أنه من حيث المسافة ، فإن إضافة حارة واحدة لكل طريق من حارات على كل جانب يعادل إضافة ثلاثة حارات على جانب واحد. القرب الإقليدي في كلتا الحالتين سوف يتضاعف. مثيرة للاهتمام.



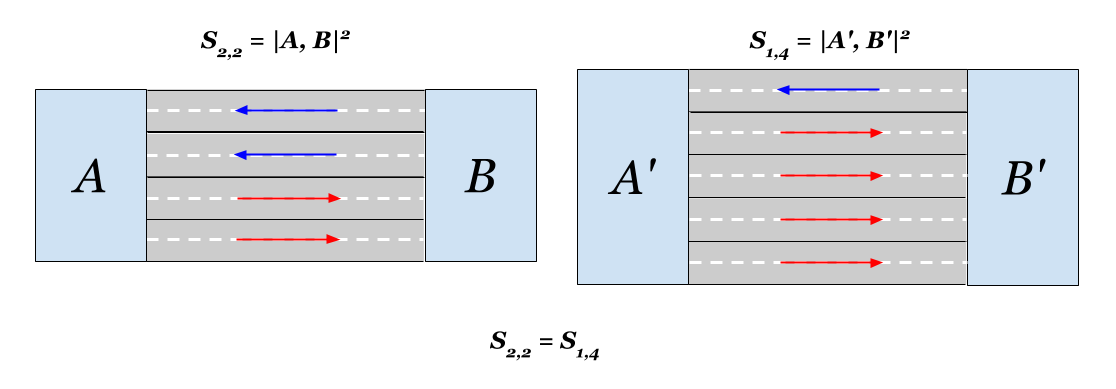
هذا كل شيء. شكرا لاهتمامكم).