حيث تتلاقى الأدلة والحقائق والخيال

في الرياضيات ، حيث يكون الإثبات هو كل شيء ، فإن الحقائق مهمة أيضًا. ومع ذلك ، فإن الحقائق جيدة ، فقط في حين أن النموذج جيد ، وبناء النماذج مهنة لا يمكن الاعتماد عليها. إذن كم من الحقائق ستكون كافية؟

يمكنك العثور على الرقم التالي في التسلسل؟

1 ، 2 ، 4 ، 8

فيما يلي رقم واحد إذا كنت بحاجة إلى المزيد من البيانات من أجل اتخاذ قرار:

1 ، 2 ، 4 ، 8 ، 16

يجب أن يكون الرقم التالي 32 ، أليس كذلك؟ النمط واضح: للعثور على الرقم التالي ، تحتاج إلى مضاعفة الرقم السابق. 1 × 2 = 2 ؛ 2 × 2 = 4 ؛ 4 × 2 = 8 ؛ 8 × 2 = 16. لذا ، يجب أن يكون الرقم التالي 16 × 2 = 32. كم عدد الحقائق الإضافية المطلوبة لتأكيد هذا؟

لكن على الرغم من أنه من المعقول افتراض أن الرقم التالي هو 32 ، فإن هذا لن يكون دائمًا صحيحًا. ضع في اعتبارك التسلسل التالي: سنحسب عدد الأقسام التي تنقسم بها الدائرة بخطوط تربط النقاط الموجودة على الدائرة.



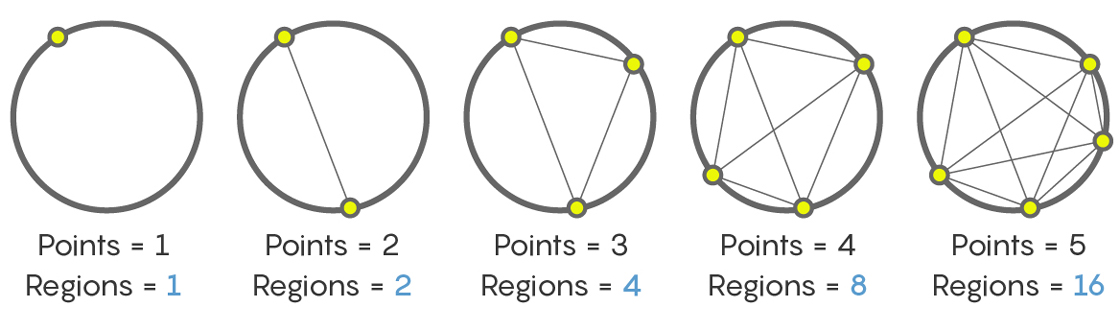
نقطة واحدة يعطي قسم واحد (الجزء الداخلي بأكمله من الدائرة). نقطتين - قسمين. ثلاث نقاط - أربعة أقسام. خمسة وستة هم ثمانية وستة عشر ، على التوالي. والنتيجة هي تسلسل

1 ، 2 ، 4 ، 8 ، 16

وكم عدد الأقسام التي ستظهر بعد ربط خطوط الست نقاط على الدائرة؟ لن يدينك أحد إذا قلت لك ، مثل كثيرين ممن واجهوا هذه المهمة لأول مرة ، أن 32. لكن هذا ليس كذلك. في الواقع ، بغض النظر عن مدى مزعج ، فإن الجواب سيكون - 31! إعادة حساب نفسك ، ثم تحقق مرة أخرى.



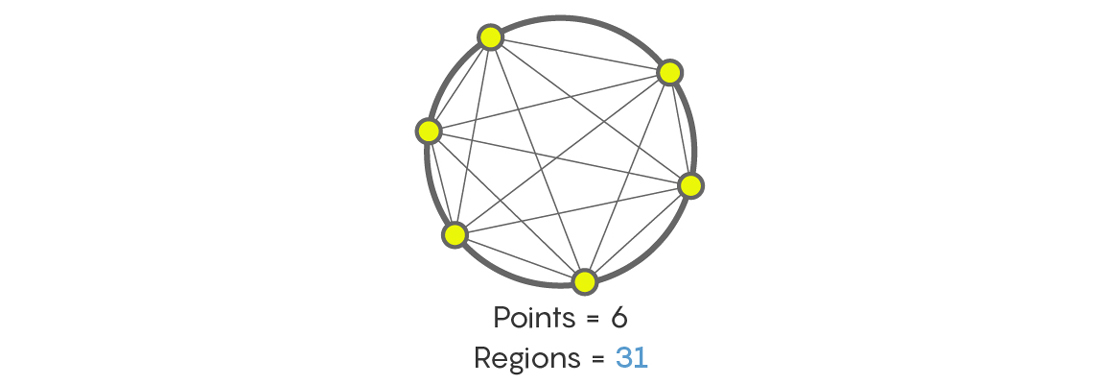
بالطبع ، هناك تسلسلات مثل 1 و 2 و 4 و 8 و 16 و 32 و 64 ، وما إلى ذلك ، من الأرقام تتضاعف في كل مرة. ولكن هناك تسلسلات أخرى ، على سبيل المثال ، الحد الأقصى لعدد الأقسام التي تنقسم فيها الدائرة بخطوط تربط النقاط الموجودة في الدائرة ، وهي 1 و 2 و 4 و 8 و 16 و 31 و 57 و 99 وما إلى ذلك. بالوصول إلى التسلسل 1 ، 2 ، 4 ، 8 ، 16 ، قد نعتقد أن كل الحقائق هي أن الرقم التالي سيكون 32 ، ولكن قد يكون هناك شيء آخر.

الرياضيات لديها تقليد طويل من تحدي توقعاتنا وجعل خيالنا يعمل. لذلك ، يسعى علماء الرياضيات دائمًا للحصول على دليل صارم ، وليس فقط الحقائق. الدليل يثبت الحقيقة الرياضية. قد تشير جميع الحقائق إلى 32 كرقم لاحق في تسلسلنا ، لكن بدون إثبات صارم لا يمكننا التأكد من ذلك.

ولكن لا يزال ، حقائق علماء الرياضيات مفيدة ومهمة. قبل إثبات شيء ما ، نلعب غالبًا بالمعلومات المتاحة ودراسة المشكلة ودراسة الأمثلة وجمع البيانات. ندرس ونزن الحقائق ونقرر ما يجب القيام به بعد ذلك. هذه النتائج تشكل رأينا ، نقترح إثبات بعض النظريات ودحض الآخرين.

فرضية التوأم الأساسي هي أحد الأمثلة التي تتحكم فيها الحقائق في تفكيرنا الرياضي بنفس طريقة الإثبات. الأعداد الأولية المزدوجة هي أزواج من الأعداد الأولية تختلف بمقدار 2 - على سبيل المثال ، 3 و 5 و 11 و 13 و 101 و 103. تشير فرضية الأعداد الأولية المزدوجة إلى أنه لا يوجد زوج أكبر من التوائم - وهذا مشابه تظهر أزواج باستمرار على خط الأرقام عند الانتقال إلى ما لا نهاية.

فرضية التوأم الأول ليست نظرية ، لأنه على الرغم من حقيقة أن هذه واحدة من أكثر المشاكل شهرة في نظرية الأعداد ، لم يتمكن أحد من إثبات ذلك. ومع ذلك ، يعتقد الجميع تقريبًا أن هذا صحيح ، نظرًا لوجود العديد من الحقائق في دعمه.

على سبيل المثال ، في بحثنا عن الأعداد الأولية نجد باستمرار أزواج كبيرة للغاية من الأعداد الأولية المزدوجة. يحتوي كل من الأعداد الأولية لأكبر زوج معروف اليوم على 400000 رقم. كما أثبتت نظريات مماثلة لهذه الفرضية. في عام 2013 ، صدمت تشانغ إيثان المجتمع الرياضي بإثبات وجود عدد كبير لا حصر له من أزواج الأعداد الأولية ، والتي لا تزيد عن 70 مليون. بفضل مشروع Polymath المفتوح الذي أعقب ذلك ، نعلم أن هناك عددًا لا حصر له من أزواج الأعداد الأولية التي تختلف بما لا يزيد عن 246 . لم نثبت بعد وجود عدد لا حصر له من أزواج الأعداد الأولية التي تختلف بمقدار 2 - ولكن لا يزال 2 أقرب بكثير من 246 إلى 246 إلى ما لا نهاية.

لهذه الأسباب وغيرها ، فإن الإيمان بالعدالة ، حتى لو لم تثبت الفرضية ، ليس مثيرًا للجدل. ومع ذلك ، هناك مجالات أخرى في الرياضيات تستخدم فيها الحقائق لبناء آراء مستنيرة تتحول إلى أكثر إثارة للجدل.

في دراسة المنحنيات الإهليلجية ، تشير رتبتها ، تقريبًا ، إلى تقدير عددي لتعقيد حل هذا المنحنى. لسنوات عديدة كان يُعتقد أن صفوف المنحنيات الإهليلجية ليست محدودة ، أي أنه لا توجد قيود على قيمة رتبة المنحنى أو تعقيد الحل.

ومع ذلك ، فإن العمل الأخير يجعل علماء الرياضيات يفكرون في إمكانية الحصول على رتبة محدودة. تقدم الورقة حقائق تشير إلى أنه من الممكن أن يكون هناك عدد محدود من المنحنيات التي تزيد رتبتها عن 21.

ومع ذلك ، ينصح الحذر. الحقائق التي جمعها علماء الرياضيات ليست مأخوذة من عالم المنحنيات الإهليلجية - إنها تتعلق بالمصفوفات التي استخدمها الباحثون لتصميم المنحنيات. تُستخدم النماذج الرياضية على نطاق واسع في العلوم ، ويمكن حتى تحويلها إلى الداخل لدراسة الرياضيات نفسها. هذه أدوات قوية بشكل لا يصدق تسمح لنا باستبدال مهمة غير مفهومة بمهمة يسهل علينا التعامل معها.

ولكن استخدام النماذج هو عمل صعب. لا يمكنك أبدًا التأكد من أن النموذج يتصرف تمامًا مثل ما نحاول فهمه ، حتى نتمكن من استخلاص استنتاجات من سلوكه. أيضا ، لا يمكن للمرء أن يكون متأكدا من أن نموذجنا متشابه على وجه التحديد في الأماكن ذات الأهمية الكبرى. لذلك ، من الصعب التأكد من أن الحقائق التي جمعناها على أساس النماذج تشهد حقًا على الخصائص الحقيقية للظواهر التي ندرسها. دعنا ندرس هذه المشكلات بناءً على نموذج بسيط لفرضية بسيطة.

تخيل أننا نريد دراسة العبارة التالية: أي سطرين إما متقاطعين أو متوازيين.

نعني بالتقاطع وجود خطوط مستقيمة في نقاط مشتركة ، وبالتوازي مع حقيقة أنها تسير في اتجاه واحد ولكن لا تتقاطع (يمكن تعريف هذا المفهوم بشكل مختلف ، لكنني سأستخدم هذا للبساطة).

لدراسة هذه المشكلة ، قم بإنشاء نموذج. يتم تمثيل كل سطر بمعادلة الخط المائل ، والتي يمكنك تذكرها من الدورة المدرسية. بمعنى ، نفترض أنه يمكن وصف كل سطر بمعادلة النموذج

y = mx + b

حيث m هو ميل الخط (انحداره) ، و b هي نقطة تقاطع المحور y (المحور العمودي).

خطوط النمذجة بهذه الطريقة ملائمة للتجارب عليها. يسمح لنا النموذج بإنشاء خط عشوائي عن طريق اختيار زوج من الأرقام العشوائية ، m و b. يمكننا اختيار زوج من الخطوط العشوائية والتحقق منها - هل تتقاطع؟ هل يذهبون في اتجاه واحد؟ هل يحدث أي شيء آخر؟

فيما يلي بعض الأمثلة على النتائج التي قد تبدو عليها مثل هذه التجارب.



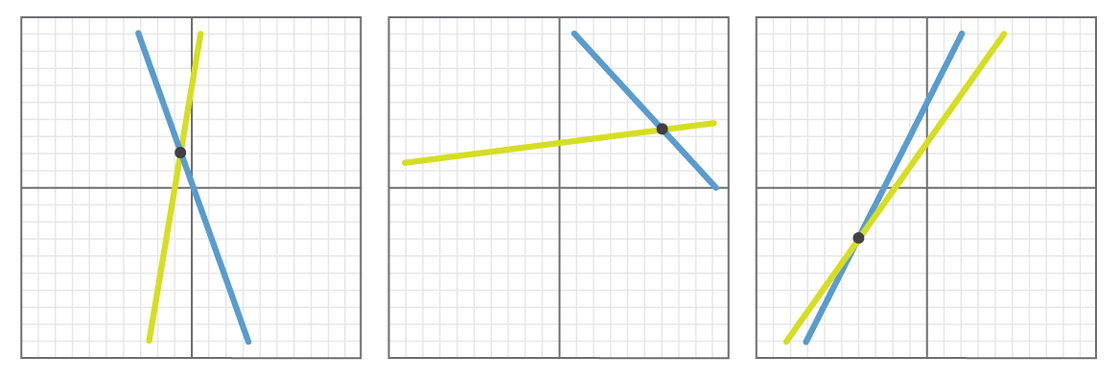
في كل مثال ، تتقاطع الخطوط المحددة عشوائياً. إذا أجرينا هذه التجربة ألف مرة - أو 10000 ، أو مليون - فسوف نجد في جميع الحالات أن الخطوط ستتقاطع أو تكون متوازية (والأرجح أن تتقاطع جميع الخطوط ، لأنه من غير المرجح أن يكون للخطين نفس الميل ، تم اختيارهما عن طريق الصدفة).

لذلك ، بالنظر إلى مليون مثال ، يمكنك التوصل إلى استنتاج مفاده أن الفرضية على الأرجح صحيحة. كل الحقائق تدعم تمامًا التصريح بأن أي زوج من الخطوط إما متوازي أو يتقاطع.

ومع ذلك ، فإن الحقائق جيدة فقط مثل النموذج جيد ، والنمذجة خطيرة. دعونا نرى ما هي المخاطر التي خلقناها لأنفسنا في مثالنا.

مشكلة واحدة هي أن أنواع معينة من الخطوط ستكون أكثر شيوعًا من غيرها. فيما يلي رسم بياني يوضح 50 سطرًا ب = 0 و 0 ≤ m ≤ 1.



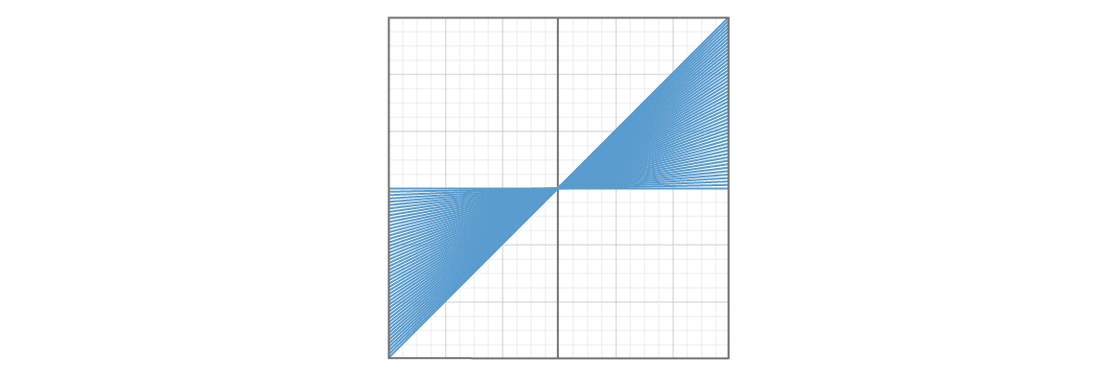
وهنا رسم بياني يوضح 50 سطرًا ب = 0 و m ≥ 1.



يبدو أن ربع الطائرة مغطى بخطوط مستقيمة ذات ميل من 0 إلى 1 ، وربع آخر مغطى بخطوط مستقيمة ذات ميل أكبر من 1. اختيار رقم أكبر من 1 يبدو أكثر احتمالًا من اختيار رقم من 0 إلى 1 ، لذلك يكون الخط المستقيم أكثر احتمالًا سيكون في القسم الثاني من الطائرة. هذا يعني أن خطوطًا معينة ، ذات ميل من 0 إلى 1 ، لن تكون ممثلة بالقدر الكافي في النموذج. وإذا حدثت بعض الأشياء الغريبة في هذا الجزء من الطائرة بخطوط مستقيمة ، فمن غير المرجح أن يخبرنا نموذجنا بهذا.

إذا نظرت عن كثب إلى المخطط الثاني ، فسنرى مشكلة أخرى. أكبر م يصبح ، وأكثر حدة الخطوط المستقيمة ستكون. أروع خط مستقيم عمودي. ما هو ميل الخط العمودي؟ بحكم التعريف ، لم يتم تعريفه: لا يوجد رقم m يمكن أن يصف الخط العمودي. اتضح أنه لا يوجد خط عمودي في نموذجنا ، ولا يمكننا تجربة ذلك. لم نبدأ بعد في جمع الحقائق ، لكننا استبعدنا بالفعل بعض الحالات الخاصة ببساطة بسبب مخطط البناء النموذجي.

نفس الشيء يتعلق بأخطر مشكلة في نموذجنا. ربما لاحظ الأشخاص الذين يتخيلون بسهولة الفضاء ثلاثي الأبعاد على الفور أن فرضيتنا خاطئة. لا يلزم أن يكون الخط المستقيم متقاطعًا أو موازياً. تخيل ممرين يسيران في اتجاهات مختلفة على طوابق مختلفة من المبنى. هذه هي خطوط مستقيمة متقاطعة - خطوط مستقيمة لا تتقاطع وليست متوازية.



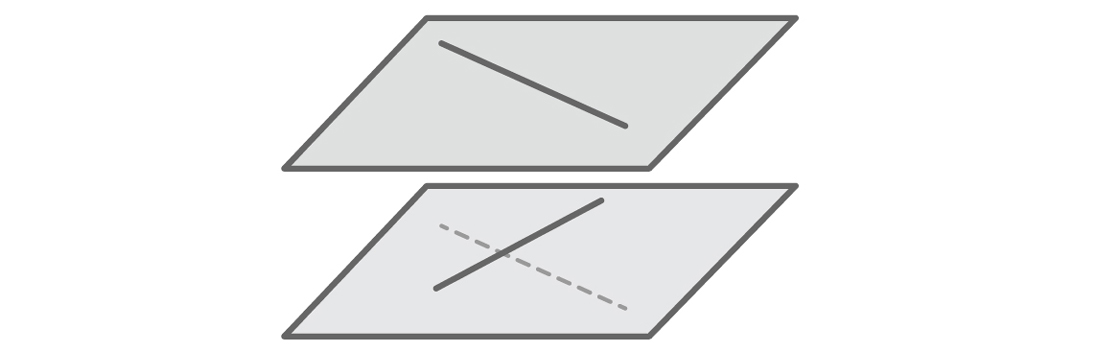
يجب أن تكمن الخطوط المتقاطعة في طائرات مختلفة. ولكن نظرًا لأن نموذجنا يحدد أي خط من خلال المعادلة y = mx + b ، فإننا نتخيل تلقائيًا أن جميع الخطوط في نفس المستوى. لن يقدم نموذجنا سوى حقائق تدعم فرضيتنا ، لأنه إذا كان هناك سطرين في نفس المستوى ، فيجب عليهما إما التقاطع أو الموازاة. لن نرى حقائق أخرى: لا توجد خطوط متقاطعة في نموذجنا. كما في حالة الخطوط العمودية ، استبعد النموذج ما لم نتخيله.

هذا مثال بسيط يستخدم نموذجًا غبيًا مع مجموعة من المشكلات ، بما في ذلك الأسئلة الصعبة ، مثل الإجراء الخاص باختيار الأرقام العشوائية من مجموعات غير محدودة. إن علماء الرياضيات المحترفين الذين يدرسون صفوف المنحنيات الإهليلجية لن يرتكبون مثل هذه الأخطاء المبسطة والواضحة.

هؤلاء علماء الرياضيات يعرفون ما هي الاحتياطات الواجب اتخاذها عند العمل مع النماذج. إنهم يعلمون أنه بغض النظر عن مدى فائدة ومدى اهتمام النموذج ، أو مدى إقناع الحقائق التي تم جمعها ، فإن المنحنيات الإهليلجية قد تكشف عن خصائص لم يتخيلوها. وإذا لم يمكن تخيل ذلك ، فلن يأخذ نموذجك هذا في الاعتبار ، وبالتالي ، فلن تنعكس الحقائق.

ولكن سواء كان النموذج الجديد صحيحًا أم لا ، فقد أجبر علماء الرياضيات على التفكير بشكل منتج في المنحنيات الإهليلجية. إذا كان هذا يعكس الحقيقة حقًا ، فبإمكان أفكار من عالم المصفوفات شرح سلوك المنحنيات. إذا لم يكن الأمر كذلك ، فإن فهم لماذا لا يمكن منحنيات الاهليلجيه على غرار هذه الطريقة يؤدي إلى فهم أفضل للمشكلة. يمكن أن تقربنا الحقائق التي نجمعها من إثبات ، بطريقة أو بأخرى.