طبقة الالتفاف: تقنيات تحسين الضرب بالمصفوفة

مقدمة

هذه المقالة هي سلسلة من المقالات التي تصف الخوارزميات الأساسية.
Synet هو إطار لإطلاق شبكات عصبية مدربة مسبقًا على وحدة المعالجة المركزية.

إذا نظرت إلى توزيع وقت المعالج الذي يتم إنفاقه على انتشار الإشارات المباشرة في الشبكات العصبية ، اتضح أن أكثر من 90٪ من الوقت يتم إنفاقه في طبقات تلافيفية. لذلك ، إذا أردنا الحصول على خوارزمية سريعة لشبكة عصبية ، نحتاج أولاً وقبل كل شيء إلى خوارزمية سريعة لطبقة تلافيفية. في هذه المقالة ، أود أن أصف طرق تحسين انتشار الإشارات المباشرة في طبقة تلافيفية. وأريد أن أبدأ بالأساليب الأكثر استخدامًا على أساس ضرب المصفوفة. سأحاول الاحتفاظ بالعرض التقديمي بأكثر أشكاله سهولة للوصول ، بحيث تكون المقالة مثيرة للاهتمام ليس فقط للمتخصصين (إنهم يعرفون كل شيء عنها بالفعل) ، ولكن أيضًا لدائرة أوسع من القراء. لا أدعي أن أكون مراجعة كاملة ، لذا فإن أي تعليقات أو إضافات مرحب بها فقط.

خيارات طبقة الالتواء

أود أن أبدأ الوصف مع وصف للمعلمات الموجودة في الطبقة التلافيفية. يمكن للخبراء بأمان تخطي هذا القسم.

أحجام الصور المدخلات والمخرجات

بادئ ذي بدء ، تتميز الطبقة التلافيفية بمدخلات وصورة مخرجات تتميز بالمعلمات التالية:

• srcC / dstC - عدد القنوات في صورة المدخلات والمخرجات. تدوين بديل: C / D.
• srcH / dstH - ارتفاع صورة المدخلات والمخرجات. التعيين البديل: H.
• srcW / dstW - عرض صورة المدخلات والمخرجات. التعيين البديل: W.
• دفعة - عدد صور المدخلات (الإخراج) - يمكن للطبقة معالجة مجموعة كاملة من الصور في وقت واحد. التعيين البديل: N.

أحجام الأساسية الالتواء

عملية الالتواء هي بطبيعتها مجموع مرجح لمنطقة معينة من نقطة معينة في الصورة. حجم النواة الإلتواءية - يميز حجم هذا الحي ويوصف بمعلمتين:

• kernelY هو ارتفاع نواة الالتواء. التعيين البديل: Y.
• kernelX هو عرض kernel الالتواء. التعيين البديل: X.

التلفاز الأكثر شيوعًا مع حجم النواة 1 × 1 و 3 × 3 . الأحجام 5 × 5 و 7 × 7 أقل شيوعًا. أحجام الإلتواء الكبيرة ، وكذلك التشابك مع نواة غير مربعة ، توجد أيضًا في بعض الأحيان ، لكن هذا أكثر غرابة.

خطوة الالتواء

معلمة مهمة أخرى هي خطوة الالتواء:

• strideY هي خطوة الالتواء العمودي.
• strideX - خطوة الالتواء الأفقي.

إذا كانت الخطوة مختلفة عن 1x1 ، على سبيل المثال - 2x2 ، فستكون صورة المخرجات بمقدار النصف (سيتم حساب الإلتواء فقط في جوار النقاط الزوجية).

تمتد الإلتواء

يمكن تمديد نواة الالتواء (زيادة حجم الإطار الفعال ، مع الحفاظ على عدد العمليات) باستخدام المعلمات التالية:

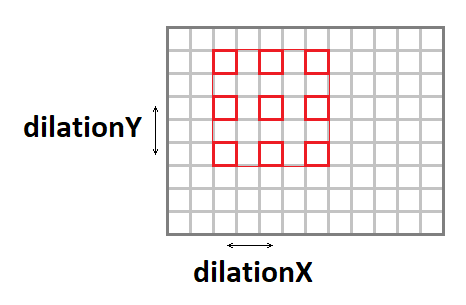
• اتساع - التمدد العمودي للالتواء.
• التمدد - الامتداد الأفقي للالتواء.

تجدر الإشارة إلى أن الحالات التي تمتد بخلاف 1x1 هي أمر نادر الحدوث (لم أصادف مثل هذا الشيء في حياتي المهنية).

الحشو صورة الإدخال

إذا قمت بتطبيق ملفوف مع نافذة مختلفة عن نافذة واحدة إلى الصورة ، فإن صورة الإخراج ستكون أقل بمقدار kernel - 1 . الحزمة ، كما كانت ، "تأكل" الحواف. للحفاظ على حجم الصورة ، غالبًا ما يتم تعبئة صورة الإدخال حول الحواف باستخدام الأصفار. هناك أربع معلمات أخرى مسؤولة عن هذا:

• padY / padX - الحشو الأمامي والأفقي الأمامي.
• padH / padW - الحشوة الخلفية العمودية والأفقية.

مجموعات القنوات

عادةً ما تكون كل قناة إخراج عبارة عن مجموع التلفيفات عبر جميع قنوات الإدخال. ومع ذلك ، هذا ليس هو الحال دائما. من الممكن تقسيم قنوات الإدخال والإخراج إلى مجموعات ، ويتم الجمع فقط داخل المجموعات:

• المجموعة - عدد المجموعات.

في الممارسة العملية ، غالباً ما تتم مواجهة المواقف مع group = 1 و group = srcC = dstC ، ما يسمى بالالتواء بعمق .

وظيفة التشرد والتفعيل

على الرغم من أن وظيفة الإزاحة والتفعيل لا يتم تضمينها رسميًا في الالتواء ، ولكن في كثير من الأحيان تتبع هاتان العمليتان الطبقة الملتوية ، لماذا يتم تضمينها أيضًا في العادة. في ضوء تنوع وظائف التنشيط الممكنة ومعلماتها ، لن أصفها هنا بالتفصيل.

التنفيذ الأساسي للخوارزمية

بادئ ذي بدء ، أود أن أقدم تطبيقًا أساسيًا للخوارزمية:

float relu(float value) { return value > 0 ? return value : 0; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int b = 0; b < batch; ++b) { for (int g = 0; g < group; ++g) { for (int dc = 0; dc < dstC / group; ++dc) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { float sum = 0; for (int sc = 0; sc < srcC / group; ++sc) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) sum += src[((b * srcC + sc)*srcH + sy)*srcW + sx] * weight[((dc * srcC / group + sc)*kernelY + ky)*kernelX + kx]; } } } dst[((b * dstC + dc)*dstH + dy)*dstW + dx] = relu(sum + bias[dc]); } } } } } } 

في هذا التطبيق ، افترضت أن صورة المدخلات والمخرجات في تنسيق NCHW :



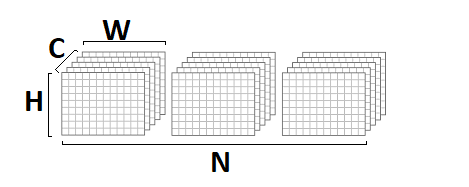
يتم تخزين أوزان الإلتفاف بتنسيق DCYX ، ووظيفة التنشيط الخاصة بنا هي ReLU . في الحالة العامة ، الأمر ليس كذلك ، ولكن بالنسبة للتطبيق الأساسي ، فإن هذه الافتراضات مناسبة تمامًا - عليك أن تبدأ من شيء ما.

لدينا 8 دورات متداخلة وإجمالي عدد العمليات:

 batch * kernelY * kernelX * srcC * dstH * dstW * dstC / group * 2, 

بينما كمية البيانات في المدخلات:

 batch * srcC * srcH * srcW, 

وإخراج الصورة:

 batch * dstC * dstH * dstW, 

وعدد الأوزان:

 kernelY * kernelX * srcC * dstC / group. 

إذا كانت المجموعة << srcC (عدد المجموعات أصغر بكثير من عدد القنوات) ، وكذلك مع المعلمات الكبيرة بما فيه الكفاية srcC و srcH و srcW و dstC ، فسنواجه مشكلة حسابية كلاسيكية عندما يتجاوز عدد العمليات الحسابية بشكل كبير مقدار بيانات المدخلات والمخرجات. أي يجب أن تعتمد عملية الالتواء مع التنفيذ السليم على موارد الحوسبة للمعالج ، وليس على عرض النطاق الترددي للذاكرة. يبقى فقط للعثور على هذا التنفيذ.

الحد من المشكلة لمصفوفة الضرب

العملية الرئيسية في الإلتفاف هي الحصول على مبلغ موزون ، والأوزان متساوية بالنسبة لجميع نقاط صورة المخرجات. إذا قمت بإعادة ترتيب صورة الإدخال كما يلي:

 void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int sc = 0; sc < srcC; ++sc) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) *buf++ = src[((b * srcC + sc)*srcH + sy)*srcW + sx]; else *buf++ = 0; } } } } } } 

ثم سننتقل من التنسيق srcC - srcH - srcW سنتحول إلى التنسيق srcC - kernelY - kernelX - dstH - dstW . يوضح الشكل أدناه كيفية تحويل الصورة باستخدام الحشو 1 و 3 × 3 :



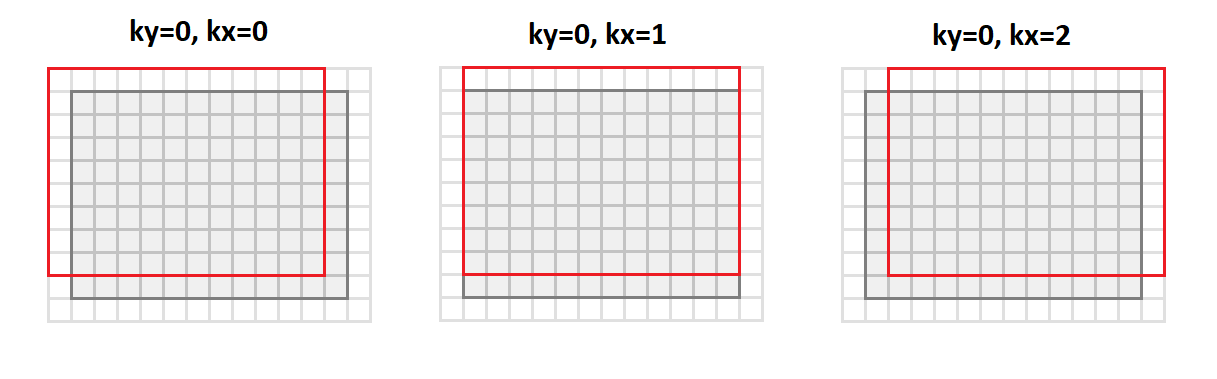
في هذه الحالة ، تتم محاذاة جميع نقاط حي الصورة المطلوبة لعملية الالتفاف على طول أعمدة المصفوفة الناتجة (ومن هنا جاءت تسميتها اسم أيم إلى أعمدة العقيد ).

يمثل التمثيل الجديد لصورة الإدخال أمرًا مثيرًا للاهتمام لأنه يتم الآن تقليل عملية الالتفاف فينا إلى ضرب المصفوفة:



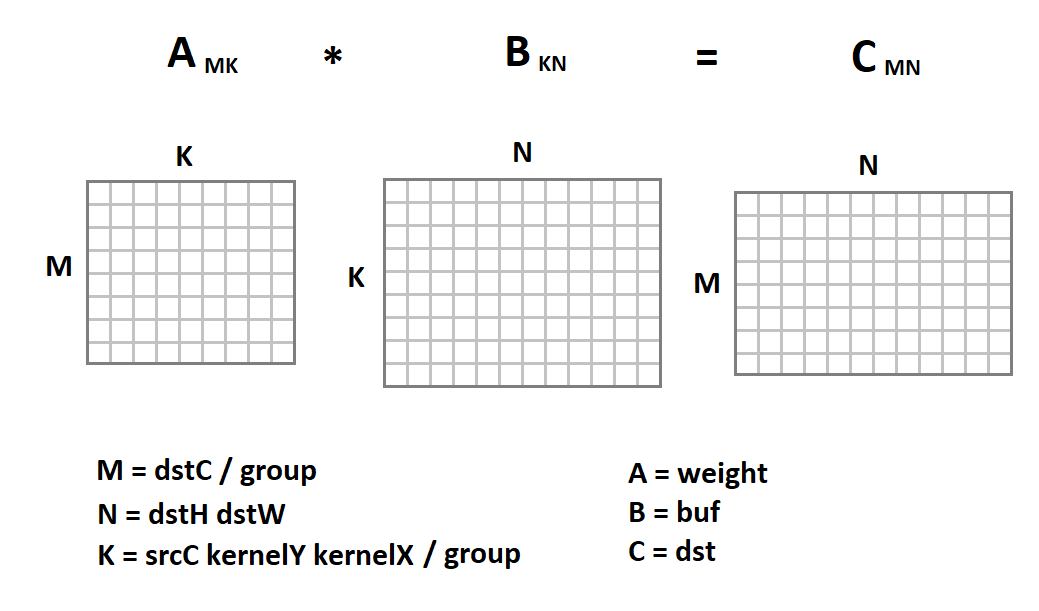
الآن سيبدو رمز الإلتفاف هكذا:

 void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) { for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; int M = dstC / group; int N = dstH * dstW; int K = srcC * kernelY * kernelX / group; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationY, strideY, strideX, padY, padX, padH, padW, buf); for (int g = 0; g < group; ++g) gemm_nn(M, N, K, 1, weight + M * K * g, K, 0, buf + N * K * g, N, dst + M * N * g, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

هنا يتم تنفيذ تافهة من الضرب مصفوفة فقط كمثال. يمكننا استبداله بأي تطبيق آخر. لحسن الحظ ، تعد عملية الضرب المصفوفة عملية قائمة منذ فترة طويلة تم تنفيذها بالفعل في العديد من المكتبات بكفاءة عالية جدًا (تصل إلى 90٪ من أداء وحدة المعالجة المركزية ممكن نظريًا). حول موضوع كيفية تحقيق هذه الكفاءة ، لدي حتى مقالة منفصلة .

باستخدام الضرب مصفوفة لتنسيق NHWC

جنبا إلى جنب مع تنسيق NCHW ، وغالبا ما تستخدم NHWC في التعلم الآلي:



على سبيل المثال ، لاحظ أن NHWC هو تنسيق Tensorflow الأصلي.

تجدر الإشارة إلى أنه بالنسبة لهذا التنسيق ، يمكن أن تؤدي عملية الالتفاف أيضًا إلى مضاعفة المصفوفة. للقيام بذلك ، من التنسيق srcH - srcW - srcC ، نقوم بترجمة الصورة الأصلية إلى التنسيق dstH - dstW - kernelY - kernelX - srcC باستخدام دالة im2row :

 void im2row(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int g = 0; g < group; ++g) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; for (int sc = 0; sc < srcC; ++sc) { if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) *buf++ = src[(sy * srcW + sx)*srcC + sc]; else *buf++ = 0; } } } } } src += srcC / group; } } 

علاوة على ذلك ، تتم محاذاة جميع نقاط حي الصورة المطلوبة لعملية الالتفاف على طول صفوف المصفوفة الناتجة (ومن هنا جاءت تسميتها اسم العمر إلى الصف s). يجب علينا أيضًا تغيير تنسيق تخزين موازين الالتفاف من تنسيق DCYX إلى تنسيق YXCD . الآن يمكننا تطبيق مصفوفة الضرب:



على عكس تنسيق NCHW ، نقوم بضرب مصفوفة الصورة بمصفوفة الوزن ، وليس العكس. التالي هو رمز دالة الالتواء:

 void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; int M = dstH * dstW; int N = dstC / group; int K = srcC * kernelY * kernelX / group; for (int b = 0; b < batch; ++b) { im2row(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationY, strideY, strideX, padY, padX, padH, padW, group, buf); for (int g = 0; g < group; ++g) gemm_nn(M, N, K, 1, buf + M * K * g, K * group, 0, weight + N * g, dstC, dst + N * g, dstC)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

مزايا وعيوب الطريقة

من البداية ، أود أن أسرد مزايا هذا النهج:

• هذه الطريقة لديها تنفيذ بسيط جدا. لا لشيء أنه يستخدم في جميع المكتبات التي أعرفها تقريبًا.
• تعد فعالية الطريقة في العديد من الحالات عالية جدًا: من وحدات النسبة المئوية في الإصدار الأساسي ، نصل إلى أكثر من 80٪ من الحد الأقصى النظري.
• النهج عالمي - لدينا رمز واحد لجميع المعلمات الممكنة للطبقة التلافيفية (وهناك الكثير منها!). لذلك ، تعمل هذه الطريقة غالبًا في الحالات التي يكون فيها للنُهج الأكثر فعالية (وبالتالي أكثر تخصصًا) قيود.
• يعمل النهج مع الأشكال الرئيسية لتنسورات الصور - NCHW و NHWC .

الآن عن العيوب:

• لسوء الحظ ، يكون الضرب القياسي للمصفوفة فعالًا بشرط أن تكون قيم المعلمات M و N و K كبيرة بدرجة كافية ، وبالإضافة إلى ذلك ، فهي تقريبًا بنفس الترتيب من حيث الحجم (تعتمد الكفاءة على حقيقة أن العدد المطلوب من الحسابات هو ~ O (N ^ 3) ، والإنتاجية المطلوبة قدرة الذاكرة ~ O (N ^ 2) ). لذلك ، إذا كانت أي من المعلمات M و N و K صغيرة ، فإن كفاءة الطريقة تنخفض بشكل حاد.
• تتطلب الطريقة تحويل بيانات الإدخال. وهذا أبعد ما يكون عن العملية المجانية. لا يمكن إهمالها إلا إذا كانت K كبيرة بدرجة كافية. وإذا أخذنا في الاعتبار أنه داخل الضرب القياسي للمصفوفة ، لا يزال هناك تحول داخلي لبيانات الإدخال ، يصبح الموقف أكثر حزنًا.
• استنادًا إلى حقيقة أن K = srcC * kernelY * kernelX / group ، تكون كفاءة الطريقة منخفضة بشكل خاص بالنسبة للطبقات التلافيفية المدخلة. وللالتفاف بشكل عميق ، تفقد طريقة المصفوفة عمومًا التنفيذ التافه.
• تتطلب هذه الطريقة معالجة إضافية لبيانات المخرجات لعملية التحول وحساب وظيفة التنشيط.
• هناك طرق رياضية أكثر فعالية لحساب الإلتواء ، والتي تتطلب عمليات أقل.

النتائج

طريقة حساب الإلتواء بناءً على ضرب المصفوفة سهلة التنفيذ وذات كفاءة عالية. لسوء الحظ ، ليست عالمية. بالنسبة لعدد من الحالات الخاصة ، توجد طرق أسرع ، أوصي وصفها بتأجيل المقالات التالية من هذه السلسلة . في انتظار ردود الفعل والتعليقات من القراء. آمل أن تكونوا مهتمين!

ملاحظة: يتم تنفيذ هذا النهج وغيره من الأساليب في إطار Convolution Framework كجزء من مكتبة Simd .
يرتكز هذا الإطار على Synet ، وهو إطار لتشغيل الشبكات العصبية المدربة مسبقًا على وحدة المعالجة المركزية.