خوارزمية دوغلاس بيكر

مقدمة

منذ وقت ليس ببعيد ، كان علي أن أعمل على تبسيط سلسلة المضلعات (وهي عملية تسمح بتقليل عدد نقاط الخطوط المتعددة ). بشكل عام ، هذا النوع من المهام شائع جدًا عند معالجة الرسومات المتجهة وعند إنشاء الخرائط. على سبيل المثال ، يمكننا أن نأخذ سلسلة تسقط نقاطها المتعددة في نفس البكسل - من الواضح أنه يمكن تبسيط كل هذه النقاط في نقطة واحدة. منذ بعض الوقت ، لم أكن أعرف عمليًا أي شيء عن هذا من كلمة "تمامًا" ، وبالتالي ، كان عليّ أن أملأ بسرعة المعرفة الضرورية حول هذا الموضوع. لكن ما أدهشني عندما لم أجد أدلة كاملة كافية على الإنترنت على الإنترنت ... اضطررت إلى البحث في مقتطفات للحصول على معلومات من مصادر مختلفة تمامًا ، وبعد التحليل ، صُنع كل شيء في صورة كبيرة. الاحتلال ليس من أكثرها متعة ، أن نكون صادقين. لذلك ، أود أن أكتب سلسلة من المقالات حول خوارزميات تبسيط السلسلة المضلعة. قررت فقط أن أبدأ بخوارزمية دوغلاس بيكر الأكثر شعبية.

وصف

تقوم الخوارزمية بتعيين الخط الأولي الأولي والمسافة القصوى (ε) ، والتي يمكن أن تكون بين polylines الأصلية والمبسطة (أي ، المسافة القصوى من نقاط الأصل إلى أقرب قسم من polyline الناتج). تقسم الخوارزمية بشكل متكرر الخط متعدد الخطوط. المدخلات إلى الخوارزمية هي إحداثيات جميع النقاط بين الأول والأخير ، بما في ذلك ، وكذلك قيمة ε. يتم الاحتفاظ النقاط الأولى والأخيرة دون تغيير. بعد ذلك ، تجد الخوارزمية النقطة الأكثر بعدًا عن الجزء الذي يتكون من الأول والأخير ( خوارزمية البحث هي المسافة من النقطة إلى القطعة ). إذا كانت النقطة تقع على مسافة أقل من ε ، فيمكن إخراج جميع النقاط التي لم يتم تحديدها بعد للحفظ من المجموعة ، ويسهل الخط المستقيم الناتج المنحنى بدقة لا تقل عن ε. إذا كانت هذه المسافة أكبر من ε ، فإن الخوارزمية تستدعي نفسها بشكل متكرر على المجموعة من نقطة البداية إلى المقدمة ومن نقطة النهاية إلى نقاط النهاية. تجدر الإشارة إلى أن خوارزمية دوغلاس بيكر لا تحتفظ بالطوبولوجيا في سياق عملها. وهذا يعني أنه نتيجة لذلك ، يمكننا الحصول على خط مع تقاطعات ذاتية. كمثال توضيحي ، خذ خط متعدد الأسطر مع مجموعة النقاط التالية: [{1؛ 5} ، {2 ؛ 3} ، {5 ؛ 1} ، {6 ؛ 4} ، {9 ؛ 6} ، {11 ؛ 4} ، {13 ؛ 3} ، {14 ؛ 2} ، {18 ؛ 5}] وانظر إلى عملية التبسيط لقيم مختلفة من ε:

الخطوط المتعددة الأصلية من مجموعة النقاط المعروضة:



خط متعدد الخطوط يساوي 0.5:



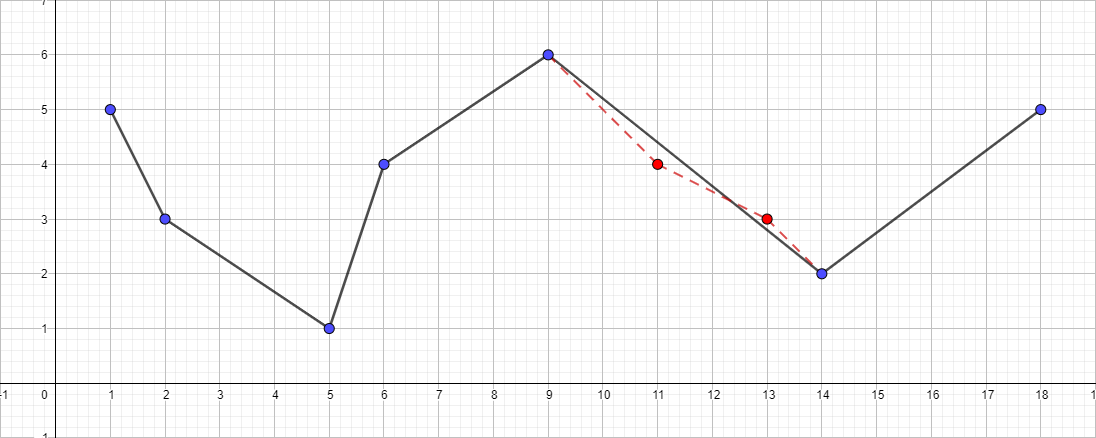
خط متعدد الخطوط يساوي 1:



متعدد الخطوط مع ε يساوي 1.5:



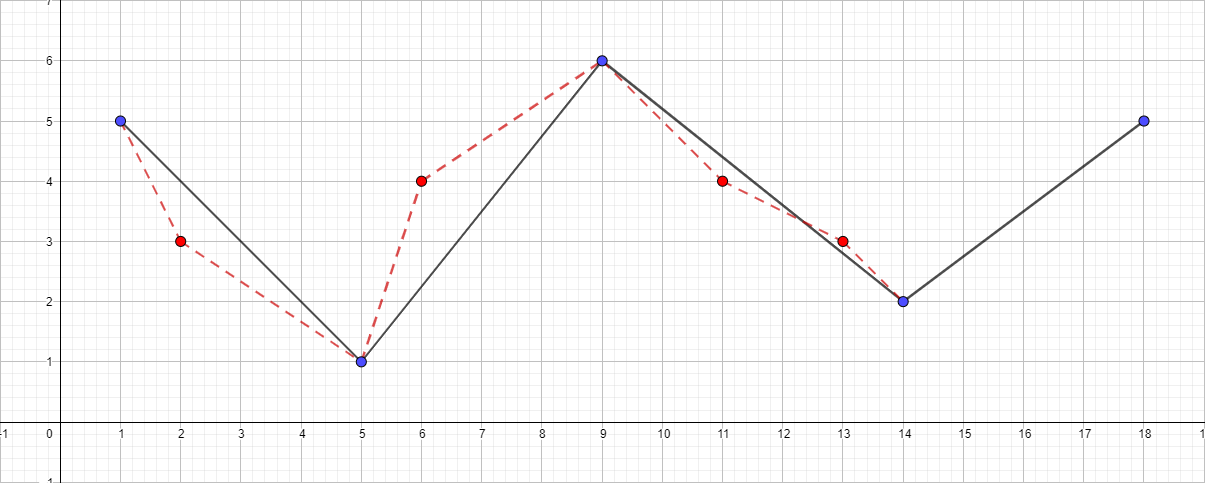
يمكنك الاستمرار في زيادة الحد الأقصى للمسافة وتصور الخوارزمية ، ولكن أعتقد أن النقطة الرئيسية بعد هذه الأمثلة أصبحت واضحة.

تطبيق

تم اختيار C ++ كلغة برمجة لتنفيذ الخوارزمية ، وهي شفرة المصدر الكاملة للخوارزمية التي يمكنك رؤيتها هنا . والآن مباشرة إلى التنفيذ نفسه:

#define X_COORDINATE 0 #define Y_COORDINATE 1 template<typename T> using point_t = std::pair<T, T>; template<typename T> using line_segment_t = std::pair<point_t<T>, point_t<T>>; template<typename T> using points_t = std::vector<point_t<T>>; template<typename CoordinateType> double get_distance_between_point_and_line_segment(const line_segment_t<CoordinateType>& line_segment, const point_t<CoordinateType>& point) noexcept { const CoordinateType x = std::get<X_COORDINATE>(point); const CoordinateType y = std::get<Y_COORDINATE>(point); const CoordinateType x1 = std::get<X_COORDINATE>(line_segment.first); const CoordinateType y1 = std::get<Y_COORDINATE>(line_segment.first); const CoordinateType x2 = std::get<X_COORDINATE>(line_segment.second); const CoordinateType y2 = std::get<Y_COORDINATE>(line_segment.second); const double double_area = abs((y2-y1)*x - (x2-x1)*y + x2*y1 - y2*x1); const double line_segment_length = sqrt(pow((x2-x1), 2) + pow((y2-y1), 2)); if (line_segment_length != 0.0) return double_area / line_segment_length; else return 0.0; } template<typename CoordinateType> void simplify_points(const points_t<CoordinateType>& src_points, points_t<CoordinateType>& dest_points, double tolerance, std::size_t begin, std::size_t end) { if (begin + 1 == end) return; double max_distance = -1.0; std::size_t max_index = 0; for (std::size_t i = begin + 1; i < end; i++) { const point_t<CoordinateType>& cur_point = src_points.at(i); const point_t<CoordinateType>& start_point = src_points.at(begin); const point_t<CoordinateType>& end_point = src_points.at(end); const double distance = get_distance_between_point_and_line_segment({ start_point, end_point }, cur_point); if (distance > max_distance) { max_distance = distance; max_index = i; } } if (max_distance > tolerance) { simplify_points(src_points, dest_points, tolerance, begin, max_index); dest_points.push_back(src_points.at(max_index)); simplify_points(src_points, dest_points, tolerance, max_index, end); } } template< typename CoordinateType, typename = std::enable_if<std::is_integral<CoordinateType>::value || std::is_floating_point<CoordinateType>::value>::type> points_t<CoordinateType> duglas_peucker(const points_t<CoordinateType>& src_points, double tolerance) noexcept { if (tolerance <= 0) return src_points; points_t<CoordinateType> dest_points{}; dest_points.push_back(src_points.front()); simplify_points(src_points, dest_points, tolerance, 0, src_points.size() - 1); dest_points.push_back(src_points.back()); return dest_points; } 

حسنا ، في الواقع استخدام الخوارزمية نفسها:

 int main() { points_t<int> source_points{ { 1, 5 }, { 2, 3 }, { 5, 1 }, { 6, 4 }, { 9, 6 }, { 11, 4 }, { 13, 3 }, { 14, 2 }, { 18, 5 } }; points_t<int> simplify_points = duglas_peucker(source_points, 1); return EXIT_SUCCESS; } 

مثال تنفيذ الخوارزمية

كمدخلات ، نأخذ مجموعة سابقة معروفة من النقاط [{1؛ 5} ، {2 ؛ 3} ، {5 ؛ 1} ، {6 ؛ 4} ، {9 ؛ 6} ، {11 ؛ 4} ، {13 ؛ 3} ، {14 ؛ 2} ، {18 ؛ 5}] و ε تساوي 1:

• أوجد أبعد نقطة من المقطع {1 ؛ 5} - {18 ؛ 5} ، ستكون هذه النقطة هي النقطة {5 ؛ 1}.
  
  
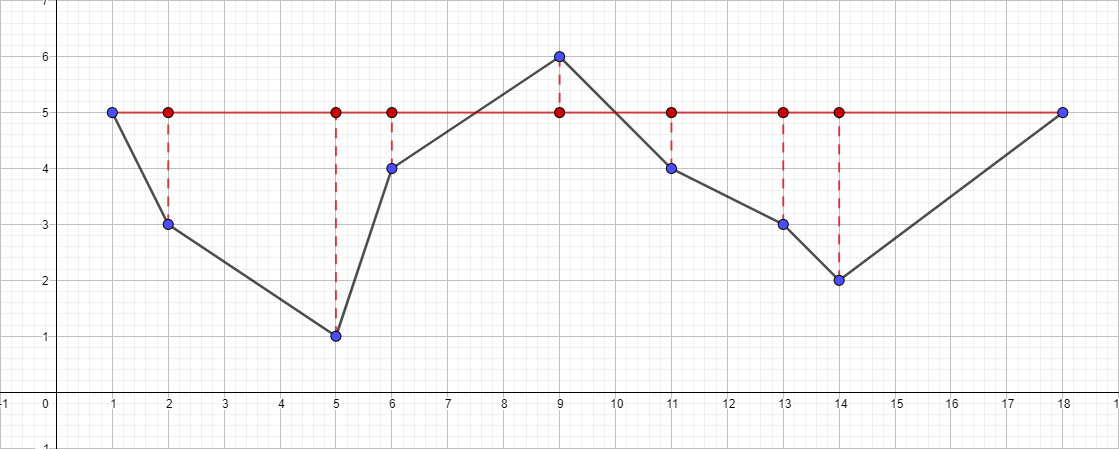
• تحقق من مسافة المسافة إلى المقطع {1 ؛ 5} - {18 ؛ (5)}. اتضح أن أكثر من 1 ، مما يعني أننا نضيفه إلى متعدد الخطوط الناتجة.
• قم بتشغيل الخوارزمية بشكل متكرر للجزء {1 ؛ 5} - {5 ؛ 1} وابحث عن النقطة الأكثر بعدًا لهذه الشريحة. هذه النقطة هي {2؛ (3)}.
  
  
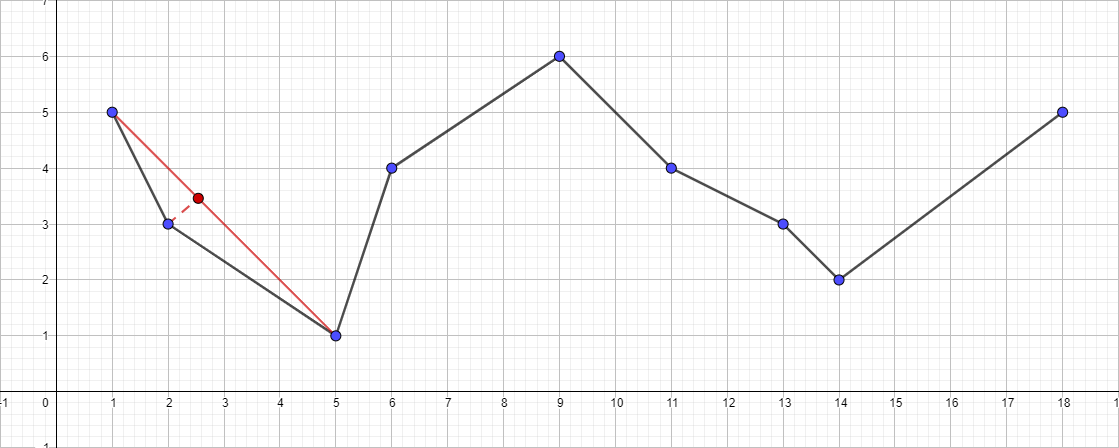
• تحقق من مسافة المسافة إلى المقطع {1 ؛ 5} - {5 ؛ 1}. في هذه الحالة ، يكون أقل من 1 ، مما يعني أنه بإمكاننا تجاهل هذه النقطة بأمان.
• قم بتشغيل الخوارزمية المتكررة للقطعة {5؛ 1} - {18 ؛ 5} وابحث عن النقطة الأكثر بُعدًا لهذا الجزء ...
  
  
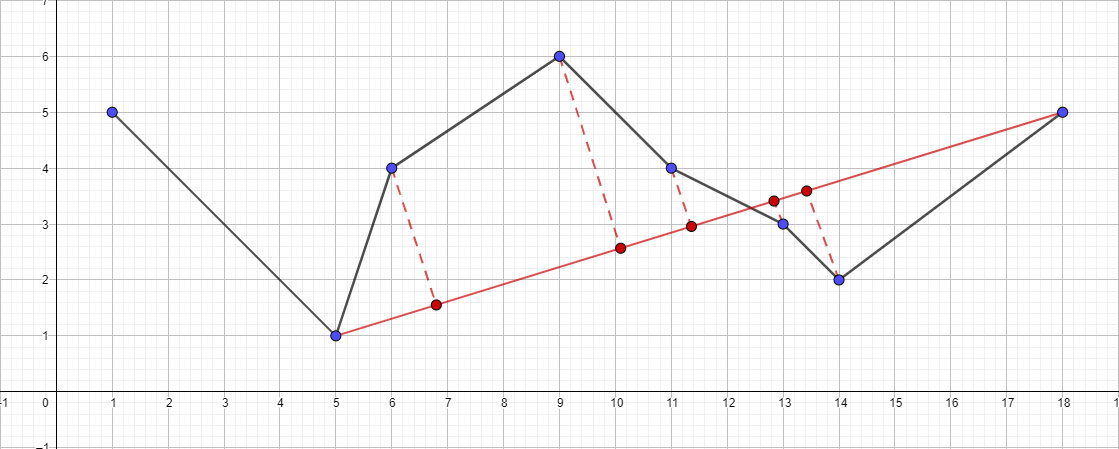
• وهلم جرا وفقا لنفس الخطة ...

نتيجة لذلك ، ستبدو شجرة النداء العودية لبيانات الاختبار هذه كما يلي:

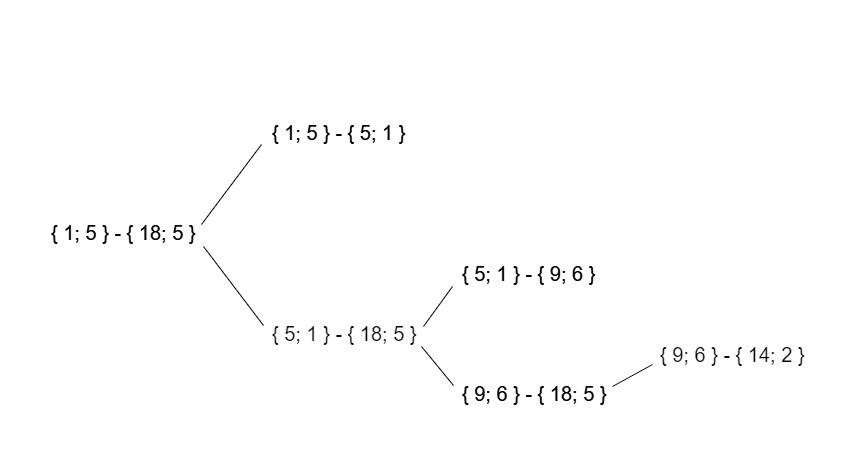
وقت العمل

التعقيد المتوقع للخوارزمية في أحسن الأحوال هو O (nlogn) ، وهذا هو عندما يكون عدد النقطة الأكثر بُعدًا دائمًا معجميًا. ومع ذلك ، في أسوأ الحالات ، يكون تعقيد الخوارزمية هو O (n ^ 2). يتم تحقيق ذلك ، على سبيل المثال ، إذا كان رقم النقطة الأكثر بُعدًا دائمًا بجوار رقم النقطة الحدودية.

آمل أن تكون مقالتي مفيدة لشخص ما ، وأود أيضًا أن أركز على حقيقة أنه إذا أظهرت المقالة اهتمامًا كافًا بين القراء ، فسوف أكون قريبًا على استعداد للنظر في خوارزميات لتبسيط سلسلة المضلعات في Reumman-Witkam و Opheim و Lang. شكرا لاهتمامكم!