عند تحليل السلاسل الزمنية الثابتة التي يتم الحصول عليها تجريبياً ، كقاعدة عامة ، أثناء الإعداد الأولي (المعالجة المسبقة) للبيانات ، يصبح من الضروري قمع الاتجاه الموجود فيها.
هنا سيتم اقتراح طريقة "جديدة" لتسليط الضوء على الاتجاه - بسيطة وواضحة ومناسبة لأنواع معقدة للغاية من الاتجاه.
عادة ما يتم فهم الاتجاه باعتباره مكونًا غير متناسق الترددات المنخفضة جدًا ينتهك بحدة المركزية للعملية. السبب الأكثر شيوعًا للاتجاه في البيانات التي تم الحصول عليها تجريبيًا هو "الانجراف الصفري" لجهاز التسجيل. يمكن أن يتسبب تكامل البيانات وبعض أنواع المعالجة الأخرى أيضًا في حدوث اتجاه. إن وجود اتجاه يشوه إلى حد كبير نتائج معالجة البيانات اللاحقة (التقدير الطيفي ، وما إلى ذلك) ، وبالتالي ، فإن إزالة الاتجاه ضروري. في بعض الحالات ، يكون الاتجاه في حد ذاته مصدرا قيما للمعلومات (على سبيل المثال ، عند تحليل الاتجاهات طويلة الأجل في العمليات الاقتصادية أو الأرصاد الجوية).
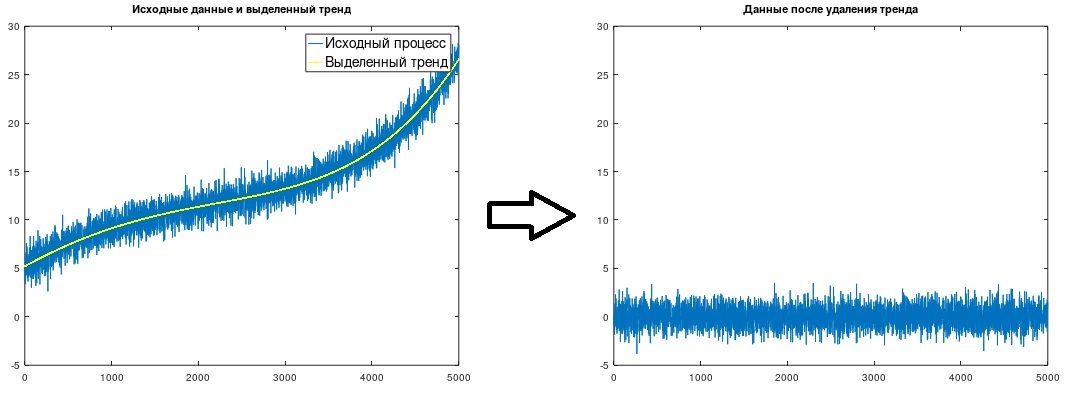التين. 1. عزل وإزالة الاتجاهعادةً ما يتم نمذجة اتجاه باستخدام الدوال الخطية أو القدرة (الترتيب الثاني أو الثالث) ، حيث يتم حساب معاملاتها بضرب العملية بتسلسلات معينة ثم تطبيق صيغ معقدة إلى حد ما مشتقة باستخدام طريقة المربعات الصغرى. (انظر ، على سبيل المثال ، J. Bendat ، A. Pirsol ، "التحليل التطبيقي للبيانات العشوائية" ، M. ، Mir ، 1989.) فيما يلي طريقة معدلة قليلاً ، تستند أيضًا إلى طريقة المربعات الصغرى ، والتي يسهل فهمها وتعلمها ، ولا يتطلب إما الرجوع إلى الدلائل ، أو الحسابات الرمزية المعقدة المستقلة للحصول على التبعيات اللازمة ، في حين يسمح لك بنمذجة الاتجاه مع وظائف من أي نوع. هذه الطريقة المعدلة بسيطة وواضحة للغاية (بمجرد إتقانها ، يمكن بعد ذلك كتابة النصوص من الذاكرة) لدرجة أنه قد تم "اختراعها" من قِبل باحثين مختلفين أكثر من مرة ، لكنني لم أصادف أي شيء في أي من المصادر حتى الآن.
لتسليط الضوء على الاتجاه ، يتم إجراء تقريب للعملية الأولية x [i] ، المكونة من عينات N + 1 ، باستخدام عدد صغير من مكونات k لوظائف الاتجاه u
j [i]:
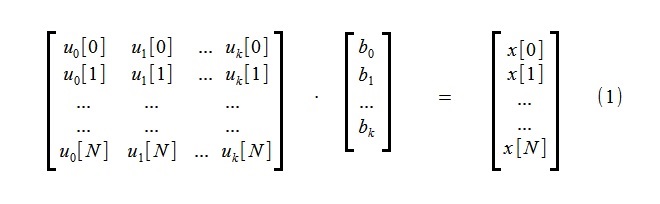
(عادة ، يتم اختيار وظائف الطاقة كوظائف u
j [i] ،
ولكن لهذه الطريقة فهي غير مبدئية على الإطلاق)
يشمل نظام المعادلات الجبرية الخطية (1) معادلات k غير معروفة b
j و N + 1.
أخذ التدوين:
الكتابة بشكل أكثر إحكاما
تطبيق طريقة المربعات الصغرى في البحث عن حل تقريبي لنظام مفرط التحديد مكتوب في شكل مصفوفة كما يلي:
عند كتابة برنامج نصي: بطبيعة الحال ، ليست هناك حاجة لتخزين المصفوفة الكبيرة بأكملها ، ويمكن "تجميع" عناصر المصفوفة U
T U والناقل U
T x خطوة بخطوة.
يتم حل النظام (4) من المعادلات k و k unknowns بطرق واضحة - حسنًا ، على سبيل المثال ، نكتبها بالشكل التالي:
بعد ذلك ، باستخدام العثور على b
j ، يمكننا بناء الاتجاه θ [i] في النموذج
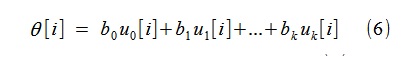
على سبيل المثال ، تم محاكاة عملية عشوائية x [i] من النموذج
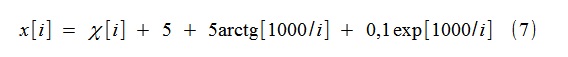
حيث χ [i] - الضوضاء البيضاء الغوسية مع تشتت واحد. تم تصميم الاتجاه من خلال وظائف من النوع (2) (بتعبير أدق ، (8)) ، وتصل إلى الترتيب الرابع (k = 4).
عند استخدام وظائف قانون القوة لنمذجة الاتجاه ، تجدر الإشارة إلى أن المصفوفة U
T U (4) يمكن عكسها نظريًا دائمًا بسبب الاستقلالية الخطية لهذه الوظائف ، ولكن بناءً على أوامر عالية من k (أو تحقيقات طويلة جدًا لـ N ، وهي أقل أهمية) ، يمكن أن تكون بعض عناصرها عظيم في القيمة المطلقة. في الطلبات العالية من k ، في حالة وجود صعوبات حسابية ، يوصى باستخدام معاملات التخفيض ، على سبيل المثال ، (8):
(Δt = 1) ، والذي تم في المثال المدروس. تم الحصول على الاتجاه الموضح في الشكل 1.
بعد تسليط الضوء على الاتجاه ، بطبيعة الحال ، ينبغي ببساطة طرحه من البيانات المصدر.
المذكرة. عادةً لا تنصح المصادر الموثوقة بالعمل مع نماذج الاتجاه للأمر أعلاه k = 2 (مكافئ مربع). سواء كان ذلك بسبب صعوبة تحديد معاملات "الاتساع" b
j بالطرق التقليدية ، أو استنفاذ أوامر متغيرات الماكينة المذكورة أعلاه ، أو التعيين الخاطئ للمكونات المعلوماتية للعملية في هذا الاتجاه ، ليس واضحًا للغاية. في المثال المحدد ، يتم تمييز اتجاه الطلب الرابع كما لو كان مقبولًا تمامًا (وإن لم يكن مختلفًا كثيرًا عن اتجاه الطلب الثالث). في الحالات الصعبة بشكل خاص ، توصي المصادر باستخدام طريقة مختلفة - تصفية تمرير منخفض (لا يتم النظر فيها هنا).
تسليط الضوء على الاتجاه ، كما هو مبين أعلاه ، فإن الإجراء ليس معقدًا للغاية ، فهو يتيح لك إما تحديد الاتجاهات "البطيئة" وتحليلها ، أو في أكثر الأحيان ، يساعد في الحصول على بيانات عالية الجودة - عملية عشوائية ثابتة مركزية مناسبة لمزيد من التحليل.