Optlib. تنفيذ خوارزمية التحسين الوراثي في ​​الصدأ

توضح هذه المقالة مكتبة optlib ، المصممة لحل مشكلات التحسين العالمية بلغة Rust. في وقت كتابة هذا التقرير ، تنفذ هذه المكتبة خوارزمية وراثية لإيجاد الحد الأدنى العام للدالة. مكتبة optlib غير مرتبطة بنوع إدخال محدد لوظيفة محسّنة. أيضًا ، تم تصميم المكتبة بطريقة تجعل من السهل عند استخدام الخوارزمية الجينية تغيير خوارزميات العبور والطفرة والاختيار والمراحل الأخرى للخوارزمية الجينية. في الواقع ، يتم تجميع الخوارزمية الجينية كما لو كانت من مكعبات.

مشكلة التحسين العالمي

عادة ما تصاغ مشكلة التحسين على النحو التالي.

بالنسبة لبعض الوظائف المعطاة f ( x ) ، من بين جميع القيم الممكنة لـ x ، ابحث عن قيمة x 'بحيث تأخذ f (x') الحد الأدنى (أو الأقصى) للقيمة. علاوة على ذلك ، يمكن أن ينتمي x إلى مجموعات مختلفة - الأعداد الطبيعية أو الأعداد الحقيقية أو الأعداد المركبة أو المتجهات أو المصفوفات.

بواسطة أقصى الدالة f ( x ) ، نعني النقطة x ' عند مشتق الدالة f ( x ) يساوي الصفر.

هناك العديد من الخوارزميات المضمونة للعثور على أقصى دالة ، وهو الحد الأدنى المحلي أو الحد الأقصى بالقرب من نقطة بداية معينة × ₀ . تتضمن هذه الخوارزميات ، على سبيل المثال ، خوارزميات النسب التدرج. ومع ذلك ، في الممارسة العملية ، غالباً ما يكون من الضروري إيجاد الحد الأدنى العالمي (أو الحد الأقصى) للدالة التي ، في نطاق معين من x ، بالإضافة إلى أقصى طرف عالمي ، له العديد من الحالات الخارجية المحلية.

لا يمكن لخوارزميات التدرج التعامل مع تحسين مثل هذه الوظيفة ، لأن حلها يتلاقى مع أقرب نقطة قرب نقطة البداية. لمشاكل إيجاد الحد الأقصى العام أو الحد الأدنى ، يتم استخدام ما يسمى خوارزميات التحسين العالمي. هذه الخوارزميات لا تضمن إيجاد حد عالمي ، لأن هي خوارزميات احتمالية ، ولكن لم يتبق سوى تجربة خوارزميات مختلفة لمهمة محددة ومعرفة الخوارزمية التي ستتعامل مع التحسين بشكل أفضل ، ويفضل أن يكون ذلك في أقصر وقت ممكن وبأقصى احتمال لإيجاد أقصى عالمي.

إحدى الخوارزميات الأكثر شهرة (والتي يصعب تنفيذها) هي الخوارزمية الجينية.

المخطط العام للخوارزمية الجينية

ولدت فكرة الخوارزمية الجينية تدريجيا وشكلت في أواخر الستينيات - أوائل السبعينيات. حصلت الخوارزميات الجينية على تطور قوي بعد إصدار كتاب جون هولاند "التكيف في النظم الطبيعية والاصطناعية" (1975)

تعتمد الخوارزمية الجينية على نمذجة مجموعة من الأفراد على عدد كبير من الأجيال. في عملية الخوارزمية الجينية ، يظهر أفراد جدد لديهم أفضل المعلمات ، ويموت الأفراد الأقل نجاحًا. للحصول على الدقة ، فيما يلي المصطلحات المستخدمة في الخوارزمية الجينية.

• الفرد هو قيمة x بين مجموعة القيم الممكنة مع قيمة الدالة الهدف لنقطة معينة x .
• الكروموسومات - قيمة x .
• كروموسوم - قيمة x _i if x عبارة عن ناقل.
• وظيفة اللياقة البدنية (وظيفة اللياقة البدنية ، الوظيفة الموضوعية) هي الوظيفة المحسنة f ( x ).
• السكان عبارة عن مجموعة من الأفراد.
• الجيل - عدد مرات تكرار الخوارزمية الجينية.

يمثل كل فرد قيمة x واحدة بين مجموعة الحلول الممكنة. يتم احتساب قيمة الوظيفة المُحسّنة (في المستقبل ، للإيجاز ، أننا نفترض أننا نبحث عن الحد الأدنى من الوظيفة) لكل قيمة x . نحن نفترض أنه كلما كانت الوظيفة الموضوعية أقل أهمية ، كان هذا الحل أفضل.

تستخدم الخوارزميات الجينية في العديد من المجالات. على سبيل المثال ، يمكن استخدامها لتحديد الأوزان في الشبكات العصبية. تستخدم العديد من أنظمة CAD خوارزمية جينية لتحسين معلمات الجهاز لتلبية المتطلبات المحددة. أيضًا ، يمكن استخدام خوارزميات التحسين العالمية لتحديد موقع الموصلات والعناصر الموجودة على السبورة.

يظهر المخطط الهيكلي للخوارزمية الجينية في الشكل التالي:

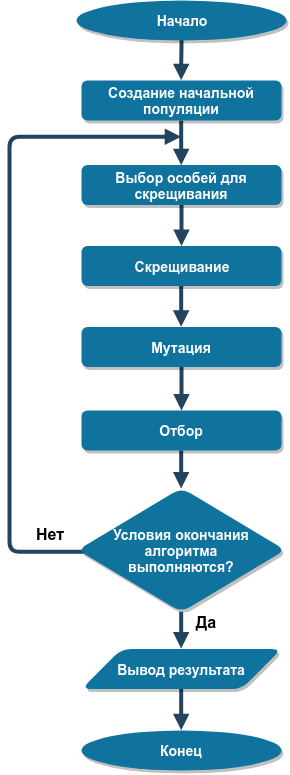
نحن نعتبر كل مرحلة من الخوارزمية بمزيد من التفصيل.

إنشاء السكان الأولي

تتمثل المرحلة الأولى من الخوارزمية في إنشاء المجموعة الأولية ، أي إنشاء العديد من الأفراد بقيم مختلفة من الكروموسومات x . كقاعدة عامة ، يتم إنشاء السكان الأولي من الأفراد الذين لديهم قيمة كروموسوم عشوائية ، بينما يحاولون التأكد من أن قيم الكروموسوم في السكان تغطي منطقة البحث عن الحل بالكامل بشكل موحد نسبيًا ، إلا إذا كانت هناك أي افتراضات فيما يتعلق بالمكان الذي يمكن أن يكون فيه أقصى العالم.

بدلاً من التوزيع العشوائي للكروموسومات ، يمكنك إنشاء الصبغيات بحيث يتم توزيع القيم الأولية لـ x بالتساوي في جميع أنحاء منطقة البحث بخطوة معينة ، والتي تعتمد على عدد الأفراد الذين سيتم إنشاءهم في هذه المرحلة من الخوارزمية.

كلما تم إنشاء المزيد من الأفراد في هذه المرحلة ، كلما زاد احتمال أن تجد الخوارزمية الحل الصحيح ، وكلما زاد حجم السكان الأولي ، كقاعدة عامة ، هناك حاجة إلى تكرار أقل للخوارزمية الجينية (عدد الأجيال). ومع ذلك ، مع زيادة حجم السكان ، هناك حاجة إلى عدد متزايد من العمليات الحسابية للوظيفة الموضوعية وأداء العمليات الوراثية الأخرى في المراحل اللاحقة من الخوارزمية. وهذا يعني أنه مع زيادة حجم السكان ، يزداد وقت حساب جيل واحد.

من حيث المبدأ ، لا يجب أن يظل حجم السكان ثابتًا طوال عمل الخوارزمية الوراثية بأكملها ، وغالبًا ما يزداد عدد الأجيال ، يمكن تقليل حجم السكان بسبب بمرور الوقت ، سيكون هناك عدد متزايد من الأفراد أقرب إلى الحل المطلوب. ومع ذلك ، في كثير من الأحيان يتم الحفاظ على حجم السكان ثابت تقريبا.

اختيار الأفراد للتهجين

بعد إنشاء مجتمع ، من الضروري تحديد الأفراد الذين سيشاركون في عملية التكاثر المتداخل (انظر الفقرة التالية). هناك العديد من الخوارزميات لهذه المرحلة. أبسطها هو عبور كل فرد مع كل فرد ، ولكن بعد ذلك في الخطوة التالية سيكون عليك القيام بالعديد من عمليات التكاثر المتداخل وحساب قيم الوظيفة الموضوعية.

من الأفضل إعطاء فرصة أكبر لتزاوج الأفراد مع كروموسومات أكثر نجاحًا (مع الحد الأدنى لقيمة الوظيفة الهدف) ، وهؤلاء الأفراد الذين تكون وظيفتهم الهدف أكثر (أسوأ) لحرمان القدرة على ترك ذرية.

وبالتالي ، في هذه المرحلة ، تحتاج إلى إنشاء أزواج من الأفراد (أو ليس بالضرورة أزواج إذا كان يمكن لعدد أكبر من الأفراد المشاركة في المعبر) ، والتي سيتم تنفيذ عملية العبور في المرحلة التالية.

هنا يمكنك أيضًا تطبيق خوارزميات مختلفة. على سبيل المثال ، قم بإنشاء أزواج بشكل عشوائي. أو يمكنك فرز الأفراد بترتيب تصاعدي حسب قيمة الوظيفة الهدف وإنشاء أزواج من الأفراد الموجودين بالقرب من بداية القائمة التي تم فرزها (على سبيل المثال ، من الأفراد في النصف الأول من القائمة ، في الثلث الأول من القائمة ، إلخ.) هذه الطريقة سيئة حيث تستغرق وقتًا فرز الأفراد.

وغالبا ما تستخدم طريقة البطولة. عندما يتم اختيار العديد من الأفراد بشكل عشوائي لدور كل مرشح للعبور ، يتم من خلاله إرسال الشخص ذو القيمة الأفضل لوظيفة الهدف إلى الزوج المستقبلي. وحتى هنا يمكن للمرء تقديم عنصر من العشوائية ، وإعطاء فرصة صغيرة للفرد صاحب أسوأ قيمة للوظيفة الهدفية "لهزيمة" الفرد بأفضل قيمة للوظيفة الهدف. يسمح لك ذلك بالحفاظ على عدد أكبر من السكان غير المتجانسين ، وحمايته من الانحطاط ، أي من موقف يكون فيه جميع الأفراد لديهم قيم كروموسوم متساوية تقريبًا ، وهو ما يعادل إيقاف الخوارزمية إلى طرف واحد ، وربما غير عالمي.

ستكون نتيجة هذه العملية قائمة شركاء للعبور.

معبر

التهجين هو عملية وراثية تخلق أشخاصًا جددًا لديهم قيم كروموسوم جديدة. يتم إنشاء كروموسومات جديدة بناءً على كروموسومات الوالدين. في معظم الأحيان ، في عملية عبور مجموعة واحدة من الشركاء ، يتم إنشاء ابنة واحدة ، ولكن من الناحية النظرية ، يمكن إنشاء المزيد من الأطفال.

يمكن أيضًا تنفيذ خوارزمية العبور بطرق مختلفة. إذا كان نوع الكروموسوم عبارة عن رقم في الأفراد ، فإن أبسط شيء يمكن القيام به هو إنشاء كروموسوم جديد باعتباره الوسط الحسابي أو الوسط الهندسي لصبغيات الوالدين. بالنسبة للعديد من المهام ، هذا يكفي ، ولكن في الغالب يتم استخدام خوارزميات أخرى تعتمد على عمليات البت.

تقاطع Bitwise العمل بطريقة تتكون كروموسوم الابنة من جزء من أجزاء أحد الوالدين وجزء من أجزاء الوالد الآخر ، كما هو موضح في الشكل التالي:

عادة ما يتم تحديد نقطة الانقسام الأصل بشكل عشوائي. ليس من الضروري إنشاء طفلين بهذا الصليب ، وغالبًا ما يقتصر على أحدهما.

إذا كانت نقطة الانقسام للكروموسومات الأصلية هي نقطة واحدة ، فإن مثل هذا العبور يسمى النقطة المفردة. ولكن يمكنك أيضًا استخدام تقسيم متعدد النقاط ، عندما تنقسم الكروموسومات الأصل إلى عدة أقسام ، كما هو مبين في الشكل التالي:

في هذه الحالة ، يمكن إجراء مجموعات أكثر من الكروموسومات الابنة.

إذا كانت الكروموسومات عبارة عن أرقام نقطية عائمة ، فيمكن تطبيق جميع الطرق الموضحة أعلاه عليها ، لكنها لن تكون فعالة للغاية. على سبيل المثال ، إذا تم تخطي أرقام الفاصلة العائمة شيئًا فشيئًا ، كما هو موضح سابقًا ، فإن العديد من عمليات العبور ستنشئ كروموسومات ابنة ستكون مختلفة عن أحد الوالدين فقط في المكان العشري البعيد. يتفاقم الموقف بشكل خاص عند استخدام أرقام الفاصلة العائمة مزدوجة الدقة.

لحل هذه المشكلة ، من الضروري التذكير بأن أرقام الفاصلة العائمة وفقًا لمعيار IEEE 754 يتم تخزينها على هيئة ثلاثة أرقام صحيحة: S (بت واحد) و M و N ، يتم حساب رقم الفاصلة العائمة منها على x = (-1) ^S × م × 2 ^ن. تتمثل إحدى طرق عبور أرقام الفاصلة العائمة في تقسيم الرقم أولاً إلى مكونات S و M و N ، وهي أعداد صحيحة ، ثم تطبيق عمليات التقاطع bitwise الموضحة أعلاه على الأرقام M و N ، حدد العلامة S لأحد الآباء والأمهات ، ومن القيم التي تم الحصول عليها لجعل ابنة كروموسوم.

في العديد من المشكلات ، لا يمتلك الفرد واحدًا ، ولكن يحتوي على العديد من الكروموسومات ، ويمكن أن يكون من أنواع مختلفة (أعداد صحيحة وأرقام الفاصلة العائمة). ثم هناك المزيد من الخيارات لعبور هذه الكروموسومات. على سبيل المثال ، عند إنشاء ابنة فردية ، يمكنك عبور جميع الكروموسومات الخاصة بالوالدين ، أو يمكنك نقل بعض الكروموسومات بالكامل من أحد الوالدين دون تغييرات.

تحول

الطفرة هي مرحلة مهمة من الخوارزمية الجينية التي تدعم تنوع الكروموسومات الفردية وبالتالي تقلل من فرص التقاء الحل بسرعة مع حد أدنى محلي بدلاً من عالمي. الطفرة هي تغيير عشوائي في كروموسوم الفرد الذي تم إنشاؤه للتو عن طريق العبور.

كقاعدة عامة ، لا يتم تعيين احتمالية حدوث طفرة عالية جدًا بحيث لا تتداخل الطفرة مع تقارب الخوارزمية ، وإلا فسوف تفسد الأفراد بالكروموسومات الناجحة.

بالإضافة إلى العبور ، يمكن استخدام خوارزميات مختلفة للتحول. على سبيل المثال ، يمكنك استبدال كروموسوم واحد أو عدة كروموسومات بقيمة عشوائية. ولكن في معظم الأحيان ، يتم استخدام طفرة في اتجاه البت عندما يتم قلب جزء واحد أو عدة أجزاء في الكروموسوم (أو في العديد من الكروموسومات) ، كما هو موضح في الأشكال التالية.

طفرة بت واحد:

طفرة عدة بتات:

يمكن أن يكون عدد البتات الخاصة بالتحور محددًا مسبقًا أو يكون متغيرًا عشوائيًا.

نتيجة للطفرات ، يمكن للأفراد أن يصبحوا أكثر نجاحًا وأقل نجاحًا ، لكن هذه العملية تسمح بوجود كروموسوم ناجح يحتوي على مجموعات من الأصفار وتلك التي لم يكن على الأبوين ظهورها باحتمال غير صفري.

اختيار

نتيجة للعبور والطفرة اللاحقة ، يظهر أفراد جدد. إذا لم تكن هناك مرحلة اختيار ، فإن عدد الأفراد سيزداد باطراد ، الأمر الذي سيتطلب المزيد والمزيد من ذاكرة الوصول العشوائي ووقت المعالجة لكل جيل جديد من السكان. لذلك ، بعد ظهور أفراد جدد ، من الضروري تطهير السكان من الأفراد الأقل نجاحًا. هذا ما يحدث في مرحلة الاختيار.

يمكن أن تكون خوارزميات التحديد مختلفة أيضًا. غالبًا ما يتم تجاهل الأفراد الذين لا تقع صبغياتهم ضمن فترة زمنية معينة من البحث عن حل.

يمكنك بعد ذلك إسقاط أكبر عدد ممكن من الأفراد الأقل نجاحًا من أجل الحفاظ على حجم السكان الثابت. يمكن أيضًا تطبيق معايير احتمالية مختلفة للاختيار ، على سبيل المثال ، قد يعتمد احتمال اختيار الفرد على قيمة الوظيفة الموضوعية.

شروط نهاية الخوارزمية

كما هو الحال في المراحل الأخرى للخوارزمية الجينية ، هناك العديد من المعايير لإنهاء الخوارزمية.

أبسط معيار لإنهاء الخوارزمية هو إحباط الخوارزمية بعد رقم معين (التكرار). ولكن يجب استخدام هذا المعيار بعناية ، لأن الخوارزمية الجينية احتمالية ، ويمكن أن تتلاقى البدايات المختلفة للخوارزمية بسرعات مختلفة. عادةً ما يتم استخدام معيار الإنهاء برقم التكرار كمعيار إضافي في حالة فشل الخوارزمية في إيجاد حل أثناء عدد كبير من التكرارات. لذلك ، يجب تعيين عدد كبير بما فيه الكفاية كحد أدنى لرقم التكرار.

معيار التوقف الآخر هو أن الخوارزمية تنقطع إذا لم يظهر حل أفضل جديد لعدد معين من التكرارات. هذا يعني أن الخوارزمية عثرت على أطراف عالمية أو عالقة في محيط محلي.

هناك أيضًا وضع غير موات عندما يكون للكروموسومات لجميع الأفراد نفس المعنى. هذا هو ما يسمى السكان المتدهورة. على الأرجح في هذه الحالة ، عالقة الخوارزمية في طرف واحد ، وليس بالضرورة عالمية. فقط الطفرة الناجحة هي القادرة على إخراج سكان من هذه الحالة ، ولكن نظرًا لأن احتمالية حدوث طفرة تكون صغيرة جدًا ، وهي بعيدة كل البعد عن حقيقة أن هذه الطفرة ستخلق فردًا أكثر نجاحًا ، فإن الحالة مع السكان المنحلين تعتبر عادةً ذريعة لإيقاف الخوارزمية الجينية. للتحقق من هذا المعيار ، من الضروري مقارنة كروموسومات جميع الأفراد ، سواء كانت هناك اختلافات بينهم ، وإذا لم تكن هناك اختلافات ، فقم بإيقاف الخوارزمية.

في بعض المشكلات ، ليس من الضروري إيجاد حد أدنى عالمي ، بل إيجاد حل جيد - حل تكون قيمة الوظيفة الهدف منه أقل من قيمة معينة. في هذه الحالة ، يمكن إيقاف الخوارزمية في وقت مبكر إذا كان الحل الموجود في التكرار التالي يفي بهذا المعيار.

optlib

Optlib هي مكتبة للغة Rust ، مصممة لتحسين الوظائف. في وقت كتابة هذه السطور ، يتم تنفيذ الخوارزمية الجينية فقط في المكتبة ، ولكن في المستقبل من المخطط توسيع هذه المكتبة عن طريق إضافة خوارزميات تحسين جديدة إليها. Optlib هو مكتوب بالكامل في الصدأ.

Optlib هي مكتبة مفتوحة المصدر يتم توزيعها بموجب ترخيص MIT.

• صفحة على جيثب - https://github.com/Jenyay/rust-optimization
• صفحة في crates.io - https://crates.io/crates/optlib
• الوثائق - https://docs.rs/optlib

optlib :: الوراثية

من وصف الخوارزمية الجينية ، يمكن ملاحظة أنه يمكن تنفيذ العديد من مراحل الخوارزمية بطرق مختلفة ، واختيارها بحيث تتقارب الخوارزمية مع وظيفة موضوعية مع الحل الصحيح في أقل وقت ممكن.

تم تصميم الوحدة النمطية optlib ::راثية بطريقة تجعل من الممكن تجميع الخوارزمية الجينية "من مكعبات". عند إنشاء مثيل للهيكل الذي سيحدث فيه عمل الخوارزمية الجينية ، ستحتاج إلى تحديد الخوارزميات التي سيتم استخدامها لإنشاء السكان ، واختيار الشركاء ، والصلبان ، والتحول ، والاختيار ، وما هي المعايير المستخدمة لمقاطعة الخوارزمية.

تحتوي المكتبة بالفعل على الخوارزميات الأكثر استخدامًا لمراحل الخوارزمية الجينية ، ولكن يمكنك إنشاء أنواعك الخاصة التي تنفذ الخوارزميات المقابلة.

في المكتبة ، الحالة التي تكون فيها الكروموسومات عبارة عن ناقل للأرقام الكسرية ، أي عند تصغير الدالة f ( x ) ، حيث تمثل x متجه أرقام الفاصلة العائمة ( f32 أو f64 ).

مثال الأمثل باستخدام optlib :: الجينية

قبل أن نبدأ في وصف الوحدة الوراثية بالتفصيل ، فكر في مثال لاستخدامها لتقليل وظيفة Schwefel. تحسب هذه الوظيفة متعددة الأبعاد على النحو التالي:

$$

$$F (\ boldsymbol x) = 418.9829N - \ sum_ {i = 1} ^ {N} x_i \ sin (\ sqrt {| x_i |})$$

الحد الأدنى من وظيفة Schweffel في الفاصل الزمني -500 <= x _i <= 500 يقع في النقطة x ' ، حيث كل x _i = 420.9687 لـ i = 1 و 2 و ... و N وقيمة الوظيفة في هذه النقطة هي f ( x' ) = 0.

إذا كانت N = 2 ، فإن الصورة ثلاثية الأبعاد لهذه الوظيفة هي كما يلي:

النهايات تكون أكثر وضوحًا إذا قمنا ببناء خطوط المستوى لهذه الوظيفة:

يوضح المثال التالي كيفية استخدام الوحدة الوراثية للعثور على الحد الأدنى من وظيفة Schweffel. يمكنك العثور على هذا المثال في الكود المصدري في مجلد الأمثلة / الجيني-شفايفل.

//!    . //! //! y = f(x),  x = (x0, x1, ..., xi,... xn). //!      x' = (420.9687, 420.9687, ...) //!      xi - [-500.0; 500.0]. //! f(x') = 0 //! //! #  //! * ` ` -   . y = f(x). //! * `` -    , x = (x0, x1, x2, ..., xn). //! * `` -   x    . //! * `` -  . //! * `` -    . use optlib::genetic; use optlib::genetic::creation; use optlib::genetic::cross; use optlib::genetic::goal; use optlib::genetic::logging; use optlib::genetic::mutation; use optlib::genetic::pairing; use optlib::genetic::pre_birth; use optlib::genetic::selection; use optlib::genetic::stopchecker; use optlib::testfunctions; use optlib::Optimizer; ///    type Gene = f32; ///   type Chromosomes = Vec<Gene>; fn main() { //   //  .  xi     [-500.0; 500.0] let minval: Gene = -500.0; let maxval: Gene = 500.0; //      let population_size = 500; //   xi  . //  15-   let chromo_count = 15; let intervals = vec![(minval, maxval); chromo_count]; //      ( ) //      optlib::testfunctions let goal = goal::GoalFromFunction::new(testfunctions::schwefel); //       . // RandomCreator       . let creator = creation::vec_float::RandomCreator::new(population_size, intervals.clone()); //        //     . let partners_count = 2; let families_count = population_size / 2; let rounds_count = 5; let pairing = pairing::Tournament::new(partners_count, families_count, rounds_count); //   //      , //   -     let single_cross = cross::FloatCrossExp::new(); let cross = cross::VecCrossAllGenes::new(Box::new(single_cross)); //    //    (     ). let mutation_probability = 15.0; let mutation_gene_count = 3; let single_mutation = mutation::BitwiseMutation::new(mutation_gene_count); let mutation = mutation::VecMutation::new(mutation_probability, Box::new(single_mutation)); // .       , //     . let pre_births: Vec<Box<genetic::PreBirth<Chromosomes>>> = vec![Box::new( pre_birth::vec_float::CheckChromoInterval::new(intervals.clone()), )]; //    //   ,       1e-4 //   3000  (). let stop_checker = stopchecker::CompositeAny::new(vec![ Box::new(stopchecker::Threshold::new(1e-4)), Box::new(stopchecker::MaxIterations::new(3000)), ]); //    .  -   . //        NaN  Inf. //    ,     . let selections: Vec<Box<dyn genetic::Selection<Chromosomes>>> = vec![ Box::new(selection::KillFitnessNaN::new()), Box::new(selection::LimitPopulation::new(population_size)), ]; //     . //       , //       . let loggers: Vec<Box<genetic::Logger<Chromosomes>>> = vec![ Box::new(logging::StdoutResultOnlyLogger::new(15)), Box::new(logging::TimeStdoutLogger::new()), ]; //     let mut optimizer = genetic::GeneticOptimizer::new( Box::new(goal), Box::new(stop_checker), Box::new(creator), Box::new(pairing), Box::new(cross), Box::new(mutation), selections, pre_births, loggers, ); //    optimizer.find_min(); } 

يمكن تشغيل هذا المثال من الجذر المصدر عن طريق تشغيل الأمر

 cargo run --bin genetic-schwefel --release 

يجب أن تبدو النتيجة مثل هذا:

 Solution: 420.962615966796875 420.940093994140625 420.995391845703125 420.968505859375000 420.950866699218750 421.003784179687500 421.001281738281250 421.300537109375000 421.001708984375000 421.012603759765625 420.880493164062500 420.925079345703125 420.967559814453125 420.999237060546875 421.011505126953125 Goal: 0.015625000000000 Iterations count: 3000 Time elapsed: 2617 ms 

وتشارك معظم رمز العينة في إنشاء كائنات سمة لمراحل مختلفة من الخوارزمية الجينية. كما هو مكتوب في بداية المقال ، يمكن تنفيذ كل مرحلة من مراحل الخوارزمية الجينية بطرق مختلفة. لاستخدام الوحدة النمطية optlib ::راثية ، تحتاج إلى إنشاء كائنات سمات تنفذ كل خطوة بطريقة أو بأخرى. بعد ذلك ، يتم نقل كل هذه الكائنات إلى مُنشئ بنية GeneticOptimizer ، والتي يتم من خلالها تنفيذ الخوارزمية الجينية.

تبدأ طريقة find_min () الخاصة ببنية GeneticOptimizer في تنفيذ الخوارزمية الجينية.

الأنواع الأساسية والكائنات

السمات الأساسية لوحدة optlib

تم تطوير مكتبة optlib بهدف إضافة خوارزميات تحسين جديدة في المستقبل بحيث يمكن للبرنامج التبديل بسهولة من خوارزمية تحسين إلى أخرى ، وبالتالي فإن وحدة optlib تحتوي على سمة Optimizer ، والتي تتضمن طريقة واحدة - find_min () ، الذي يقوم بتشغيل خوارزمية التحسين عند التنفيذ. هنا النوع T هو نوع الكائن ، وهو نقطة في مساحة البحث عن الحل. على سبيل المثال ، في المثال أعلاه ، هذا هو Vec <Gene> (حيث Gene هو اسم مستعار لـ f32). وهذا هو ، وهذا هو النوع الذي يتم تغذية كائن له لإدخال وظيفة الهدف.

تم إعلان سمة Optimizer في الوحدة النمطية optlib كما يلي:

 pub trait Optimizer<T> { fn find_min(&mut self) -> Option<(&T, f64)>; } 

يجب أن تُرجع طريقة find_min () optim_ trait's كائنًا من النوع Option <(& T ، f64)> ، حيث يمثل T & t في المجموعة المستردة الحل ، و f64 هي قيمة الدالة الهدف للحل الموجود. إذا لم تتمكن الخوارزمية من إيجاد حل ، فيجب أن ترجع الدالة find_min () بلا.

نظرًا لأن العديد من خوارزميات تحسين الاستوكاستك تستخدم عوامل تسمى (من حيث الخوارزمية الجينية ، العامل هو الفرد) ، تحتوي الوحدة النمطية optlib أيضًا على سمة AlgorithmWithAgents باستخدام طريقة get_agents () مفردة والتي يجب أن تعيد ناقل العامل.

العامل ، بدوره ، هو هيكل يقوم بتنفيذ سمة أخرى من optlib - Agent .

يتم التصريح عن الخوارزميات معithAgents و Agent في الوحدة النمطية optlib كما يلي:

 pub trait AlgorithmWithAgents<T> { type Agent: Agent<T>; fn get_agents(&self) -> Vec<&Self::Agent>; } pub trait Agent<T> { fn get_parameter(&self) -> &T; fn get_goal(&self) -> f64; } 

لكل من AlgorithmWithAgents و Agent ، النوع T له نفس المعنى بالنسبة لـ Optimizer ، أي أنه نوع الكائن الذي يتم حساب قيمة الدالة الهدف له.

هيكل الوراثة - تطبيق الخوارزمية الجينية

يتم تطبيق كلا النوعين على بنية GeneticOptimizer - Optimizer و AlgorithmWithAgents.

يتم تمثيل كل مرحلة من الخوارزمية الجينية بنوعها الخاص ، والذي يمكن تنفيذه من نقطة الصفر أو استخدام أحد تطبيقات optlib :: الجينية المتاحة في الداخل. لكل مرحلة من مراحل الخوارزمية الجينية ، داخل الوحدة النمطية optlib :: الوراثية ، هناك وحدة فرعية ذات بنى ووظائف مساعدة تنفذ الخوارزميات الأكثر استخدامًا لمراحل الخوارزمية الجينية. حول هذه الوحدات سيتم مناقشتها أدناه. يوجد أيضًا داخل بعض هذه الوحدات الفرعية وحدة فرعية vec_float تنفذ خطوات الخوارزمية للحالة عندما يتم حساب الوظيفة الهدفية من متجه بأرقام الفاصلة العائمة (f32 أو f64).

تم إعلان مُنشئ بنية GeneticOptimizer كما يلي:

 impl<T: Clone> GeneticOptimizer<T> { pub fn new( goal: Box<dyn Goal<T>>, stop_checker: Box<dyn StopChecker<T>>, creator: Box<dyn Creator<T>>, pairing: Box<dyn Pairing<T>>, cross: Box<dyn Cross<T>>, mutation: Box<dyn Mutation<T>>, selections: Vec<Box<dyn Selection<T>>>, pre_births: Vec<Box<dyn PreBirth<T>>>, loggers: Vec<Box<dyn Logger<T>>>, ) -> GeneticOptimizer<T> { ... } ... } 

يقبل مُنشئ GeneticOptimizer أنواعًا كثيرة من الكائنات التي تؤثر على كل مرحلة من مراحل الخوارزمية الجينية ، وكذلك ناتج النتائج:

• الهدف: مربع <dyn الهدف <T>> - وظيفة الهدف ؛
• stop_checker: Box <dyn StopChecker <T>> - معيار الإيقاف ؛
• منشئ: Box <dyn Creator <T>> - إنشاء السكان الأولي ؛
• الاقتران: مربع <dyn الاقتران <T>> - خوارزمية لاختيار شركاء للعبور ؛
• cross: Box <dyn Cross <T>> - خوارزمية العبور ؛
• طفرة: مربع <dyn Mutation <T>> - خوارزمية طفرة ؛
• التحديدات: Vec <Box <dyn التحديد <T> >> - متجه لخوارزميات التحديد ؛
• pre_births: Vec <Box <dyn PreBirth <T> >> - متجه من الخوارزميات لتدمير الكروموسومات غير الناجحة قبل تكوين الأفراد ؛
• قطع الاشجار: VEC <Box <dyn Logger <T> >> - متجه من الكائنات التي تحافظ على سجل الخوارزمية الجينية.

لتشغيل الخوارزمية ، يجب تنفيذ طريقة find_min () لسمة Optimizer. بالإضافة إلى ذلك ، تتضمن بنية GeneticOptimizer طريقة next_iterations () ، والتي يمكن استخدامها لمتابعة الحساب بعد اكتمال طريقة find_min ().

في بعض الأحيان بعد إيقاف الخوارزمية ، من المفيد تغيير معلمات الخوارزمية أو الطرق المستخدمة. يمكن القيام بذلك باستخدام الطرق التالية لهيكل GeneticOptimizer: replace_pairing () ، replace_cross () ، replace_mutation () ، replace_pre_birth () ، replace_selection () ، replace_stop_checker (). تسمح لك هذه الطرق باستبدال كائنات السمات التي تم تمريرها إلى بنية GeneticOptimizer عند إنشائها.

تتم مناقشة الأنواع الرئيسية للخوارزمية الجينية في الأقسام التالية.

سمة الهدف - وظيفة موضوعية

يتم الإعلان عن سمة الهدف في الوحدة النمطية optlib ::راثية كما يلي:

 pub trait Goal<T> { fn get(&self, chromosomes: &T) -> f64; } 

يجب أن تُرجع طريقة get () قيمة الوظيفة الهدف للكروموسوم المحدد.

داخل الوحدة النمطية optlib :: genetic :: target ، هناك بنية GoalFromFunction التي تنفذ سمة الهدف. لهذا الهيكل ، هناك مُنشئ يأخذ وظيفة ، وهي الوظيفة المستهدفة. وهذا هو ، باستخدام هذه البنية ، يمكنك إنشاء كائن نوع الهدف من وظيفة عادية.

سمة المنشئ - إنشاء مجموعة أولية

تصف سمة الخالق "المنشئ" للمجموعة الأولية. يتم الإعلان عن هذه السمة على النحو التالي:

 pub trait Creator<T: Clone> { fn create(&mut self) -> Vec<T>; } 

يجب أن تقوم طريقة create () بإرجاع متجه الكروموسومات التي سيتم إنشاء التعداد الأولي لها.

بالنسبة للحالة التي يتم فيها تحسين وظيفة العديد من أرقام الفاصلة العائمة ، فإن الوحدة النمطية optlib :: genetic :: creator :: vec_float لها بنية <G> RandomCreator لإنشاء توزيع أولي للكروموسومات بطريقة عشوائية.

فيما يلي ، النوع <G> هو نوع كروموسوم واحد في ناقل كروموسوم (أحيانًا يستخدم مصطلح "جين" بدلاً من مصطلح "كروموسوم"). بشكل أساسي ، يعني النوع <G> النوع f32 أو f64 إذا كانت الكروموسومات هي النوع Vec <f32> أو Vec <f64>.

يتم الإعلان عن بنية RandomCreator <G> كما يلي:

 pub struct RandomCreator<G: Clone + NumCast + PartialOrd> { ... } 

هنا NumCast هو نوع من قفص الأسطوانات . يسمح لك هذا النوع بإنشاء نوع من أنواع رقمية أخرى باستخدام أسلوب ().

لإنشاء بنية RandomCreator <G> ، تحتاج إلى استخدام الدالة () الجديدة ، والتي تم التصريح عنها على النحو التالي:

 pub fn new(population_size: usize, intervals: Vec<(G, G)>) -> RandomCreator<G> { ... } 

حجم السكان هنا هو حجم السكان (عدد مجموعات الكروموسومات المزمع إنشاؤها) ، والفواصل هي متجه للطبقة المكونة من عنصرين - الحد الأدنى والحد الأقصى لقيمة الكروموسوم المقابل (الجين) في مجموعة الكروموسومات ، وحجم هذا المتجه يحدد عدد الكروموسومات كل فرد.

في المثال أعلاه ، تم تحسين وظيفة Schweffel لـ 15 متغيرات من النوع f32. يجب أن يقع كل متغير في النطاق [-500؛ 500]. وهذا يعني ، لإنشاء مجتمع ، يجب أن يحتوي متجه الفاصل 15 tuples (-500.0f32 ، 500.0f32).

اكتب الاقتران - اختيار الشركاء للعبور

يتم استخدام سمة الاقتران لتحديد الأفراد الذين سيتم تهجينهم. يتم الإعلان عن هذه السمة على النحو التالي:

 pub trait Pairing<T: Clone> { fn get_pairs(&mut self, population: &Population<T>) -> Vec<Vec<usize>>; } 

تأخذ طريقة get_pairs () مؤشرًا إلى بنية السكان ، والتي تحتوي على جميع الأفراد في المجموعة ، وأيضًا من خلال هذا الهيكل يمكنك اكتشاف أفضل وأسوأ الأفراد في السكان.

يجب أن تُرجع طريقة get_pairs () الاقتران متجهًا يحتوي على متجهات تخزن مؤشرات الأفراد الذين سيتزاوجون. بناءً على خوارزمية التقاطع (التي سيتم مناقشتها في القسم التالي) ، يمكن لشخصين أو أكثر عبورها.

على سبيل المثال ، إذا تم تجاوز الأفراد الذين لديهم الفهرس 0 و 10 و 5 و 2 و 6 و 3 ، فيجب أن تُرجع طريقة get_pairs () vec vector! [Vec! [0، 10]، vec! [5، 2]، vec! [ 6 ، 3]].

تحتوي الوحدة النمطية optlib :: الجينية :: الاقتران على هيكلين يطبقان خوارزميات اختيار الشركاء المختلفة.

بالنسبة لبنية RandomPairing ، يتم تطبيق نوع الاقتران بطريقة يتم اختيار الشركاء بشكل عشوائي للعبور.

بالنسبة لهيكل البطولة ، يتم تطبيق سمة الاقتران بطريقة تستخدم طريقة البطولة. تعني طريقة البطولة أن كل فرد يشارك في الصليب يجب أن يهزم فردًا آخر (يجب أن تكون قيمة الوظيفة الموضوعية للفرد الفائز أقل). إذا كانت طريقة البطولة تستخدم جولة واحدة ، فإن هذا يعني أنه يتم اختيار شخصين بشكل عشوائي ، وأن الشخص ذي القيمة المنخفضة للوظيفة الموضوعية بين هذين الشخصين يدخل في "الأسرة" المستقبلية. إذا تم استخدام عدة جولات ، فيجب أن يفوز الفرد الفائز بهذه الطريقة ضد العديد من الأفراد العشوائيين.

تم إعلان مُنشئ بنية الدورة على النحو التالي:

 pub fn new(partners_count: usize, families_count: usize, rounds_count: usize) -> Tournament { ... } 

هنا:

• partners_count - العدد المطلوب من الأفراد للعبور ؛
• العائلات - عدد "العائلات" ، أي مجموعات من الأفراد الذين سوف ينتجون ذرية ؛
• rounds_count - عدد الجولات في البطولة.

كتعديل إضافي لطريقة البطولة ، يمكنك استخدام مولد الأرقام العشوائية لإعطاء فرصة صغيرة لهزيمة الأفراد الذين لديهم أسوأ قيمة للوظيفة الهدف ، أي لجعل احتمالية النصر تتأثر بقيمة الوظيفة الموضوعية ، وكلما زاد الفرق بين المتنافسين ، زادت فرصة الفوز بأفضل فرد ، ومع وجود قيم متساوية تقريبًا للوظيفة الهدفية ، سيكون احتمال فوز فرد واحد قريبًا من 50٪.

اكتب عبور

بعد تشكيل "أسر" الأفراد ، للعبور ، تحتاج إلى عبور الكروموسومات للحصول على أطفال مع كروموسومات جديدة. تتمثل مرحلة العبور بنوع الصليب ، والذي يتم الإعلان عنه على النحو التالي:

 pub trait Cross<T: Clone> { fn cross(&mut self, parents: &[&T]) -> Vec<T>; } 

تعبر الطريقة () مجموعة واحدة من الآباء. تقبل هذه الطريقة المعلمة الخاصة بالوالدين - شريحة من الإشارات إلى الكروموسومات الخاصة بالوالدين (وليس الأفراد أنفسهم) - ويجب أن تعيد ناقلًا من الكروموسومات الجديدة. يعتمد حجم الآباء على الخوارزمية الخاصة باختيار الشركاء للعبور باستخدام ميزة الإقران ، والتي تم وصفها في القسم السابق. غالبًا ما تستخدم خوارزمية تنشئ كروموسومات جديدة تعتمد على كروموسومات من والدين ، عندها سيكون حجم الوالدين مساوٍ لاثنين.

تحتوي الوحدة النمطية optlib :: genetic :: cross على هياكل يتم من خلالها تطبيق النوع المتقاطع مع خوارزميات متقاطعة مختلفة.

• VecCrossAllGenes - هيكل مصمم لعبور الكروموسومات ، عندما يكون لدى كل فرد مجموعة من الكروموسومات - هذا ناقل. يقبل مُنشئ VecCrossAllGenes نوع كائن متقاطع سيتم تطبيقه على جميع عناصر متجهات كروموسوم الأصل. في هذه الحالة ، يجب أن يكون حجم متجهات كروموسوم الأصل بنفس الحجم. يستخدم المثال أعلاه بنية VecCrossAllGenes لأن الكروموسوم في الأفراد المستخدمين هو نوع Vec <f32>.
• CrossMean عبارة عن هيكل يعبر عن رقمين بحيث يكون كروموسوم ابنة بمثابة رقم يتم حسابه على أنه المتوسط ​​الحسابي للكروموسومات الأصل.
• إن FloatCrossGeometricMean عبارة عن هيكل يتقاطع مع رقمين ، بحيث يكون كروموسوم ابنة بمثابة رقم يتم حسابه باعتباره المتوسط ​​الهندسي للكروموسومات الأصل. يجب أن يكون هناك أرقام النقطة العائمة كروموسومات.
• CrossBitwise - تقاطع أحادي الاتجاه من رقمين.
• FloatCrossExp - تقاطع نقطي أحادي الاتجاه لأرقام الفاصلة العائمة. عبقرية مستقلة والعارضين الوالدين تعبر. يتلقى الطفل علامة من أحد الوالدين.

تحتوي الوحدة النمطية optlib :: genetic :: cross أيضًا على وظائف لأرقام التقاطع bitwise لأنواع مختلفة - عدد صحيح ونقطة عائمة.

اكتب طفرة - طفرة

بعد العبور ، من الضروري تحور الأطفال الذين تم الحصول عليهم من أجل الحفاظ على تنوع الكروموسومات ، ولم ينزلق السكان إلى حالة التدهور. بالنسبة للسكان ، فإن ميزة تحور الصفة مخصصة ، والتي يتم الإعلان عنها على النحو التالي:

 pub trait Mutation<T: Clone> { fn mutation(&mut self, chromosomes: &T) -> T; } 

تأخذ الطريقة الوحيدة للطفرة () الخاصة بـ Mutation إشارة إلى كروموسوم ويجب أن ترجع كروموسومًا محتمل التغيير. كقاعدة عامة ، هناك احتمال ضئيل لحدوث طفرة ، على سبيل المثال ، نسبة مئوية قليلة ، بحيث تظل الكروموسومات التي تم الحصول عليها على أساس الوالدين لا تزال قائمة ، وبالتالي تحسين السكان.

بعض خوارزميات الطفرة مطبقة بالفعل في الوحدة النمطية optlib :: genetic :: mutation .

تحتوي هذه الوحدة ، على سبيل المثال ، على بنية VecMutation ، والتي تعمل بشكل مشابه لهيكل VecCrossAllGenes ، أي إذا كان الكروموسوم متجهًا ، يقبل VecMutation نوع كائن Mutation ويطبقه مع وجود احتمال محدد لجميع عناصر المتجه ، مما ينشئ متجهًا جديدًا به جينات متحولة (عناصر متجه الصبغيات).

تحتوي الوحدة النمطية optlib :: genetic :: mutation أيضًا على بنية BitwiseMutation التي يتم تطبيق سمة Mutation عليها. يحول هذا الهيكل عددًا معينًا من البتات العشوائية في الكروموسوم المنقول إليها. يُنصح باستخدام هذا الهيكل مع بنية VecMutation.

سمة ما قبل الولادة - الاختيار المسبق

بعد العبور والطفرة ، عادة ما تحدث مرحلة الاختيار ، حيث يتم تدمير أكثر الأفراد غير الناجحين. ومع ذلك ، عند تنفيذ الخوارزمية الجينية في مكتبة optlib :: الوراثية ، قبل خطوة التحديد ، هناك خطوة أخرى يمكن عندها التخلص من الكروموسومات غير الناجحة. تمت إضافة هذه الخطوة لأن حساب الوظيفة الموضوعية للأفراد غالبًا ما يستغرق الكثير من الوقت ، ولا توجد حاجة لحسابها إذا لم تقع الصبغيات في فاصل البحث المعروف. على سبيل المثال ، في المثال أعلاه ، الكروموسومات التي لا تقع على الجزء [-500؛ 500].

لتنفيذ عملية التصفية المسبقة هذه ، تكون سمة PreBirth مخصصة ، والتي يتم الإعلان عنها على النحو التالي:

 pub trait PreBirth<T: Clone> { fn pre_birth(&mut self, population: &Population<T>, new_chromosomes: &mut Vec<T>); } 

طريقة preBirth () الوحيدة لسمات PreBirth هي إشارة إلى بنية السكان المذكورة أعلاه ، بالإضافة إلى إشارة قابلة للتغيير إلى متجه الكروموسومات الجديد. هذا هو ناقل الكروموسومات التي تم الحصول عليها بعد خطوة الطفرة. يجب أن يؤدي تنفيذ طريقة pre_birth () إلى إزالة تلك الكروموسومات من هذا المتجه والتي من الواضح أنها غير مناسبة لحالة المشكلة.

بالنسبة للحالة التي يتم فيها تحسين وظيفة ناقل أرقام الفاصلة العائمة ، تحتوي الوحدة النمطية optlib ::راثية :: pre_birth :: vec_float على هيكل CheckChromoInterval ، المصمم لإزالة الكروموسومات إذا كانت متجهًا لأرقام الفاصلة العائمة ، وبعض عنصر المتجه لا يقع في الفاصل الزمني المحدد.

مُنشئ بنية CheckChromoInterval كما يلي:

 pub fn new(intervals: Vec<(G, G)>) -> CheckChromoInterval<G> { ... } 

هنا ، يأخذ المُنشئ متجهًا من tuples مع عنصرين - الحد الأدنى والحد الأقصى لقيمة كل عنصر في الكروموسوم. وبالتالي ، يجب أن يتزامن حجم ناقل الفواصل الزمنية مع حجم ناقل كروموسوم الأفراد. في المثال أعلاه ، تم استخدام متجه مكون من 15 tuples (-500.0f32 ، 500.0f32) كفواصل زمنية.

اختيار اختيار - اختيار

بعد الاختيار الأولي للكروموسومات ، يتم تكوين الأفراد ووضعهم في السكان (الهيكل السكاني ). في عملية تكوين الأفراد لكل منهم ، يتم حساب قيمة الوظيفة الهدف. في مرحلة الاختيار ، من الضروري تدمير عدد معين من الأفراد حتى لا ينمو السكان إلى أجل غير مسمى. لهذا ، يتم استخدام سمة التحديد ، والتي يتم التصريح عنها على النحو التالي:

 pub trait Selection<T: Clone> { fn kill(&mut self, population: &mut Population<T>); } 

يجب أن يستدعي الكائن الذي يقوم بتطبيق خاصية التحديد في طريقة الفتح () طريقة الفتح () للبنية الفردية (الفردية) لكل فرد في المجموعة التي تحتاج إلى تدمير.

لتجاوز جميع الأفراد في مجتمع ما ، يمكنك استخدام أداة تكرار تقوم بإرجاع أسلوب IterMut () في بنية السكان.

نظرًا لأنه من الضروري في كثير من الأحيان تطبيق العديد من معايير الاختيار ، عند إنشاء بنية GeneticOptimizer ، فإن المُنشئ يقبل متجه كائنات نوع التحديد.

كما هو الحال مع المراحل الأخرى من الخوارزمية الجينية ، تقدم وحدة optlib :: الجينية :: الانتقاء بالفعل عدة تطبيقات لمرحلة الاختيار.

• KillFitnessNaN - يدمر الأفراد التي تكون فيها قيمة الوظيفة الهدف NaN أو Inf.
• LimitPopulation - يدمر مثل هذا العدد من أسوأ الأفراد بحيث لا يتجاوز حجم السكان حجمًا معينًا.
• optlib :: genetic :: select :: vec_float :: CheckChromoInterval - في حالة تحسين وظيفة المتجه للأرقام الفاصلة العائمة ، فإنه يدمر الأفراد الذين لا تتناسب قيمة كروموسومهم مع الفواصل الزمنية المحددة. تعمل هذه البنية بشكل مشابه للبنية optlib ::راثية :: pre_birth :: vec_floatCheckChromoInterval للمرحلة السابقة من الخوارزمية الجينية.

StopChecker سمة - معيار التوقف

بعد مرحلة الاختيار ، تحتاج إلى التحقق مما إذا كان الوقت قد حان لإيقاف الخوارزمية الجينية. كما سبق ذكره أعلاه ، في هذه المرحلة ، يمكنك أيضًا استخدام العديد من خوارزميات التوقف. بالنسبة إلى مقاطعة الخوارزمية ، يكون الكائن مسؤولًا عن تطبيق سمة StopChecker ، والتي تم إعلانها على النحو التالي:

 pub trait StopChecker<T: Clone> { fn can_stop(&mut self, population: &Population<T>) -> bool; } 

هنا يجب أن ترجع طريقة can_stop () صوابًا إذا كان يمكن إيقاف الخوارزمية ، وإلا فإن هذه الطريقة يجب أن تُرجع خطأ.

تحتوي الوحدة النمطية optlib :: genetic :: stopchecker على العديد من الهياكل ذات معايير التوقف الأساسية وبنيان لإنشاء مجموعات من معايير أخرى:

• MaxIterations - كسر المعيار حسب رقم الجيل. ستتوقف الخوارزمية الجينية بعد عدد معين من التكرارات (الأجيال).
• GoalNotChange - أحد معايير الاستراحة التي بموجبها يجب أن تتوقف الخوارزمية إذا تعذر العثور على حل جديد لعدد معين من التكرارات. أو بعبارة أخرى ، إذا لم يظهر عدد من الأفراد الناجحين لعدد أكبر من الأجيال.
• الحد الفاصل - هو معيار التوقف الذي بموجبه تنقطع الخوارزمية الجينية إذا كانت قيمة الوظيفة الموضوعية للحل الأفضل في الوقت الحالي أقل من قيمة العتبة المحددة.
• CompositeAll — , ( - StopChecker). , - , .
• CompositeAny — , ( - StopChecker). , - , .

Logger —

Logger , , , . Logger :

 pub trait Logger<T: Clone> { ///       fn start(&mut self, _population: &Population<T>) {} ///     , ///           fn resume(&mut self, _population: &Population<T>) {} ///         /// (    ) fn next_iteration(&mut self, _population: &Population<T>) {} ///      fn finish(&mut self, _population: &Population<T>) {} } 

optlib::genetic::logging , Logger:

• StdoutResultOnlyLogger — ;
• VerboseStdoutLogger — .
• TimeStdoutLogger — , .

يقبل مُنشئ بنية GeneticOptimizer ، كالوسيطة الأخيرة ، متجهًا لأنواع أحرف Logger ، والذي يسمح لك بتكوين ناتج البرنامج بمرونة.

وظائف لاختبار خوارزميات التحسين

وظيفة شوفيل

لاختبار خوارزميات التحسين ، تم اختراع الكثير من الوظائف مع العديد من extrema المحلية. وحدة optlib :: testfunctions يحتوي على العديد من الوظائف، والتي يمكن اختبارها الخوارزميات. في وقت كتابة هذا التقرير ، تحتوي الوحدة النمطية optlib :: testfunctions على وظيفتين فقط.

إحدى هذه الوظائف هي وظيفة Schweffel ، التي كتبت عنها في بداية المقال. مرة أخرى ، أذكر أن هذه الوظيفة مكتوبة على النحو التالي:

$$

$$F(\boldsymbol x) = 418.9829N - \sum_{i=1}^{N}x_i \sin (\sqrt{|x_i|})$$

x' = (420.9687, 420.9687, ...). .

optlib::testfunctions schwefel . N .

, , , , .

:

$$

$$F(\boldsymbol x) = \sum_{i=1}^{N} (x_i - n)^2$$

x' = (1.0, 2.0,… N). .

optlib::testfunctions paraboloid .

استنتاج

optlib , . ( optlib::genetic ), , , , .

optlib::genetic. . , , , , .

, . , ( , ..)

بالإضافة إلى ذلك ، من المزمع إضافة وظائف تحليلية جديدة (بالإضافة إلى وظيفة Schweffel) لاختبار خوارزميات التحسين.

أذكر مرة أخرى الروابط المرتبطة بمكتبة optlib:

• صفحة على جيثب - https://github.com/Jenyay/rust-optimization
• صفحة في crates.io - https://crates.io/crates/optlib
• الوثائق - https://docs.rs/optlib

وإنني أتطلع إلى تعليقاتكم والإضافات والتعليقات.