تنوعا والكمال التجزئة

نبدأ الأسبوع بمواد مفيدة مخصصة لإطلاق الدورة التدريبية "الخوارزميات للمطورين" . هل لديك قراءة جيدة.



1. نظرة عامة

Hashing هو أداة عملية رائعة ، مع نظرية مثيرة للاهتمام ورائعة. بالإضافة إلى استخدام البيانات كهيكل مفردات ، يوجد تجزئة في العديد من المجالات المختلفة ، بما في ذلك نظرية التشفير ونظرية التعقيد. في هذه المحاضرة ، وصفنا مفهومين مهمين: التجزئة العالمي (المعروف أيضًا باسم العائلة الشاملة لوظائف التجزئة) والتجزئة المثالية.

تشمل المواد التي تم تسليط الضوء عليها في هذه المحاضرة ما يلي:

• الإعداد الرسمي والفكرة العامة للتجزئة.
• التجزئة العالمية.
• التجزئة الكمال.

2. مقدمة

سننظر في المشكلة الرئيسية في القاموس التي ناقشناها من قبل ، وسننظر في إصدارين: ثابت وديناميكي:

• ثابت : نظرًا للعديد من عناصر S ، نريد تخزينه بطريقة يمكننا من خلالها إجراء بحث سريعًا.
• على سبيل المثال ، قاموس ثابت.
• ديناميكي : هنا لدينا سلسلة من طلبات الإدراج ، والبحث ، وربما الإزالة. نريد أن نفعل كل هذا على نحو فعال.

بالنسبة للمشكلة الأولى ، يمكننا استخدام مجموعة مصنفة والبحث الثنائي. للمرة الثانية ، يمكننا استخدام شجرة بحث متوازنة. ومع ذلك ، يوفر التجزئة أسلوبًا بديلًا ، والذي غالبًا ما يكون أسرع الطرق وأكثرها ملاءمة لحل هذه المشكلات. على سبيل المثال ، افترض أنك تكتب برنامجًا للبحث عن الذكاء الاصطناعى وترغب في تخزين المواقف التي قمت بحلها بالفعل (المواضع على السبورة أو عناصر من مساحة الولاية) حتى لا تتكرر نفس العمليات الحسابية عند تشغيلها مرة أخرى. يوفر هاش طريقة سهلة لتخزين هذه المعلومات. هناك أيضا العديد من التطبيقات في التشفير ، والشبكات ، ونظرية التعقيد.

3. أساسيات التجزئة

الإعداد الرسمي للتجزئة هو كما يلي.

• تنتمي المفاتيح إلى مجموعة كبيرة من U. (على سبيل المثال ، تخيل أن U عبارة عن مجموعة من جميع السلاسل بطول 80 حرفًا ascii كحد أقصى.)
• هناك بعض مفاتيح S في U نحتاجها حقًا (يمكن أن تكون المفاتيح ثابتة أو ديناميكية). دع N = | S |. تخيل أن N أصغر بكثير من حجم U. على سبيل المثال ، S هي مجموعة أسماء الطلاب في فصل أصغر بكثير من 128 ^ 80.
• سنقوم بإجراء عمليات إدخال وإجراء بحث باستخدام صفيف A من بعض الحجم M ووظيفة هاش h: U → {0، ...، M - 1}. بالنظر إلى العنصر x ، فإن فكرة التجزئة هي أننا نريد تخزينه في A [h (x)]. لاحظ أنه إذا كانت U صغيرة (على سبيل المثال ، سلاسل ذات حرفين) ، فيمكنك فقط حفظ x في A [x] ، كما هو الحال في فرز الكتلة. المشكلة هي أن U كبير ، لذلك نحن بحاجة إلى وظيفة التجزئة.
• نحن بحاجة إلى طريقة لحل الاصطدامات. يحدث التصادم عندما يكون h (x) = h (y) لمفتاحين مختلفين x و y. في هذه المحاضرة ، سنتعامل مع التصادمات من خلال تحديد كل عنصر من عناصر A كقائمة مرتبطة. هناك عدد من الطرق الأخرى ، ولكن بالنسبة للمشكلات التي سنركز عليها هنا ، فهذه هي الطريقة الأنسب. وتسمى هذه الطريقة طريقة التسلسل. لإدراج عنصر ، نضعه ببساطة في أعلى القائمة. إذا كانت h دالة هاش جيدة ، فإننا نأمل أن تكون القوائم صغيرة.

أحد الأشياء العظيمة حول التجزئة هو أن جميع عمليات القاموس سهلة التنفيذ بشكل لا يصدق. للبحث عن المفتاح x ، قم ببساطة بحساب الفهرس i = h (x) ثم انتقل إلى القائمة في A [i] حتى تجده (أو أخرج من القائمة). للإدراج ، ضع عنصرًا جديدًا في أعلى قائمته. للحذف ، تحتاج فقط إلى تنفيذ عملية الحذف في القائمة المرتبطة. ننتقل الآن إلى السؤال التالي: ما الذي نحتاجه لتحقيق أداء جيد؟

الخصائص المرغوبة. الخصائص المرغوبة الرئيسية لمخطط التجزئة الجيد:

1. يتم توزيع المفاتيح جيدًا حتى لا يكون لدينا الكثير من التصادمات ، حيث تؤثر التصادمات على وقت البحث والحذف.
2. M = O (N): على وجه الخصوص ، نود أن تحقق دائرتنا الخاصية (1) دون الحاجة إلى أن يكون حجم الجدول M أكبر بكثير من عدد العناصر N.
3. يجب حساب الوظيفة h بسرعة. في تحليلنا اليوم ، سننظر في وقت حساب h (x) على أنه ثابت. ومع ذلك ، تجدر الإشارة إلى أنه لا ينبغي أن يكون معقدًا جدًا لأنه يؤثر على وقت التنفيذ الكلي.

بالنظر إلى ذلك ، يكون وقت البحث للعنصر x هو O (حجم القائمة هو A [h (x)]). وينطبق الشيء نفسه على الحذف. تستغرق عمليات الإدراج O (1) وقتًا بغض النظر عن طول القوائم. لذلك ، نريد أن نحلل حجم هذه القوائم.

الحدس الأساسي: طريقة واحدة لتوزيع العناصر بشكل جميل هي توزيعها بشكل عشوائي. لسوء الحظ ، لا يمكننا فقط استخدام مولد الأرقام العشوائية لتحديد مكان توجيه العنصر التالي ، لأنه لا يمكننا العثور عليه مرة أخرى. لذلك ، نريد أن نكون ح "شيئًا عشوائيًا" بطريقة ما.

الآن سوف نقدم بعض الأخبار السيئة ، ثم بعض الأخبار الجيدة.

بيان 1 (أخبار سيئة) لأي دالة هاش h إذا | U | +1 (N −1) M +1 ، هناك مجموعة S من عناصر N تم تجزئتها جميعًا في مكان واحد.

دليل: حسب مبدأ ديريتشليت. على وجه الخصوص ، للنظر في النقاط المقابلة ، إذا كان كل موقع لا يحتوي على أكثر من N - 1 من عناصر U التي تجزئته ، فيمكن أن لا يزيد حجم U عن M (N - 1).

هذا جزئيًا لماذا يبدو التجزئة غامضًا جدًا - كيف يمكن القول أن التجزئة أمر جيد إذا كان يمكنك التفكير في طرق منعه بالنسبة لأي دالة تجزئة؟ إجابة واحدة هي أن هناك العديد من وظائف التجزئة البسيطة التي تعمل بشكل جيد في مجموعات S النموذجية ، ولكن ماذا لو كنا نريد ضمانًا جيدًا للحالة الأسوأ؟

وإليك الفكرة الأساسية: دعونا نستخدم العشوائية في تصميمنا h ، على غرار الأنواع السريعة العشوائية. (وغني عن القول ، ح ستكون وظيفة حتمية). سنبين أنه لأي تسلسل لعمليات الإدراج والبحث (لا نحتاج إلى افتراض أن مجموعة العناصر المدرجة S عشوائية) ، إذا اخترنا h بهذه الطريقة الاحتمالية ، فإن أداء h في هذا التسلسل سيكون جيدًا ترقبًا. وبالتالي ، هذا هو نفس الضمان كما هو الحال في فرز سريع عشوائي أو الفخاخ. على وجه الخصوص ، هذه هي فكرة التجزئة العالمية.

بمجرد تطوير هذه الفكرة ، سنستخدمها في تطبيق ممتع بشكل خاص يسمى "تجزئة مثالية".

4. التجزئة العالمي

التعريف 1. خوارزمية عشوائية H لبناء وظائف التجزئة h: U → {1، ...، M}
إذا كان للجميع x! = ص في U لدينا



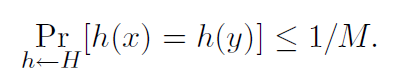
يمكننا أيضًا القول أن مجموعة H من وظائف التجزئة هي مجموعة عالمية من وظائف هاش إذا كان الإجراء "اختيار عشوائي h ∈ H" عالميًا. (هنا نحدد مجموعة الوظائف مع توزيع موحد على المجموعة.)

Theorem 2. إذا كانت H عالمية ، فبالنسبة لأي مجموعة S ⊆ من الحجم N ، لأي x ∈ U (على سبيل المثال ، يمكن أن نبحث عنها) ، إذا بنينا h بشكل عشوائي وفقًا لـ H ، فإن العدد المتوقع من الاصطدامات بين x وغيرها العناصر في S لا تزيد عن N / M.

الإثبات: كل فرصة y ∈ S (y! = X) لها على الأقل 1 / M فرصة للتصادم مع x بواسطة تعريف "شامل". على سبيل المثال،

• دع Cxy = 1 إذا اصطدمت x و y و 0 بخلاف ذلك.
• دع Cx تشير إلى إجمالي عدد حالات الاصطدام لـ x. لذا ، Cx = Py∈S ، y! = X Cxy.
• نعلم أن E [Cxy] = Pr (x و y collide) ≤ 1 / M.
• وبالتالي ، في خطي التوقع ، E [Cx] = Py E [Cxy] <N / M.

الآن نحصل على النتيجة الطبيعية التالية.

النتيجة الطبيعية 3. إذا كانت H عالمية ، فبالنسبة لأي تتابع من عمليات الإدراج والبحث والحذف L ، حيث لا يمكن أن يكون هناك أكثر من M من العناصر في النظام في وقت واحد ، فإن التكلفة الإجمالية المتوقعة لعمليات L العشوائية h هي H فقط O (L) لحساب ح كثوابت).

إثبات: بالنسبة لأي عملية معينة في التسلسل ، فإن تكلفتها المتوقعة ثابتة من خلال Theorem 2 ، وبالتالي فإن التكلفة الإجمالية المتوقعة لعمليات L هي O (L) في خطية التوقع.

السؤال: هل يمكننا فعلا بناء H عالمي؟ إذا لم يكن كذلك ، فهذا كله لا معنى له. لحسن الحظ ، الجواب هو نعم.

4.1. إنشاء عائلة تجزئة عالمية: طريقة المصفوفة

افترض أن المفاتيح طويلة جدًا. لنفترض أن حجم الجدول M يساوي الدرجة 2 ؛ لذلك ، يكون المؤشر بطول b-bit مع M = 2b.

ما سنفعله هو اختيار h كمصفوفة عشوائية 0/1 b-by-u وتحديد h (x) = hx ، حيث نضيف mod 2. هذه المصفوفات قصيرة وسميكة. على سبيل المثال:



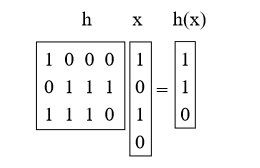
الاقتراح 4. بالنسبة إلى x! = Y Prh [h (x) = h (y)] = 1 / M = 1 / 2b.

الإثبات: أولاً ، ماذا يعني ضرب h x x؟ يمكننا التفكير في الأمر على أنه إضافة بعض الأعمدة h (القيام بتعديل إضافة ناقل 2) ، حيث يشير 1 بت في x إلى تلك التي يجب إضافتها. (على سبيل المثال ، أضفنا العمودين الأول والثالث من h أعلاه)

الآن خذ زوج مفاتيح تعسفي x ، y بحيث x! = Y. يجب أن تكون مختلفة في مكان ما ، لذلك ، على سبيل المثال ، تختلف في الإحداثي العاشر ، ومن أجل الدقة ، نقول xi = 0 و yi = 1. تخيل أننا حددنا أولاً جميع h باستثناء عمود i. بالنسبة للعينات المتبقية من العمود ith ، يتم إصلاح h (x). ومع ذلك ، يعطي كل من الإعدادات المختلفة 2b للعمود ith قيمة مختلفة لـ h (y) (على وجه الخصوص ، في كل مرة ندير فيها قليلاً في هذا العمود ، نحول البت المقابل إلى h (y)). لذلك هناك بالضبط فرصة 1 / 2b أن h (x) = h (y).

هناك طرق أخرى لبناء عائلات التجزئة الشاملة ، والتي تستند أيضًا إلى تكاثر الأعداد الأولية (انظر القسم 6.1).

السؤال التالي الذي سننظر فيه: إذا صححنا المجموعة S ، فهل يمكننا إيجاد دالة تجزئة h بحيث يكون لجميع عمليات البحث وقت ثابت؟ الجواب نعم ، وهذا يؤدي إلى موضوع التجزئة المثالي.

5. الكمال التجزئة

نقول أن دالة التجزئة مثالية لـ S في حالة حدوث جميع عمليات البحث في O (1). فيما يلي طريقتان لإنشاء وظائف تجزئة مثالية لمجموعة معينة S.

5.1 الطريقة 1: حل في الفضاء O (N2)

دعنا نقول أننا نريد أن يكون لدينا جدول بحجمه التربيعي في الحجم N من قاموسنا S. ثم هنا طريقة بسيطة لبناء وظيفة تجزئة مثالية. دع H تكون عالمية و M = N2. ثم مجرد اختيار عشوائي h من H وتجربته! البيان هو أن هناك فرصة بنسبة 50٪ على الأقل لعدم حدوث تصادمات.

الاقتراح 5. إذا كانت H عالمية و M = N2 ، فحينئذٍ Prh noH (بدون تصادم في S) ≥ 1/2.

البرهان:

• كم عدد الأزواج (س ، ص) هناك في S؟ الجواب هو:
• بالنسبة لكل زوج ، فإن احتمال تصادمهما هو ≤ 1 / M بتعريف العالمية.
• إذن Pr (هناك تصادم) ≤ / م <1/2.

هذا يشبه الجانب الآخر من "مفارقة عيد ميلاد". إذا كان عدد الأيام أكبر بكثير من عدد الأشخاص المربعة ، فهناك احتمال معقول ألا يكون للزوجين نفس عيد الميلاد.

لذلك ، نحن فقط نختار h عشوائي من H ، وإذا حدث أي تصادم ، فإننا فقط نختار h جديد. في المتوسط ​​، سنحتاج فقط إلى القيام بذلك مرتين. الآن ، ماذا لو أردنا استخدام مساحة O (N) فقط؟

5.2 الطريقة 2: حل في الفضاء O (N)

لقد كان السؤال حول ما إذا كان من الممكن تحقيق تجزئة مثالية في مساحة O (N) مفتوحًا لبعض الوقت: "هل يجب فرز الجداول؟" وهذا هو ، لمجموعة ثابتة ، يمكنك الحصول على وقت بحث مستمر فقط مع مساحة خطية؟ كانت هناك سلسلة من المحاولات أكثر وأكثر تعقيدًا ، وحتى النهاية تم حلها باستخدام فكرة جيدة عن وظائف التجزئة العالمية في مخطط ثنائي المستوى.

الطريقة هي على النحو التالي. أولاً ، سنقوم بتجزئة جدول الحجم N باستخدام التجزئة العالمي. سيؤدي ذلك إلى بعض الاصطدامات (إلا إذا كنا محظوظين). ومع ذلك ، فإننا نقوم بعد ذلك بإعادة صياغة كل سلة باستخدام الطريقة الأولى ، مع تربيع حجم السلة للحصول على أي تصادم. وبالتالي ، يتكون المخطط من حقيقة أن لدينا دالة تجزئة للمستوى الأول h وجدول A من المستوى الأول ، ثم وظائف تجزئة N للمستوى الثاني h1 و ... و hN و N للجدول الثاني من المستوى A1 و ... و A.N ... للعثور على العنصر x ، نحسب أولاً i = h (x) ، ثم نعثر على العنصر في Ai [hi (x)]. (إذا قمت بذلك من الناحية العملية ، فيمكنك تعيين العلامة بحيث لا تتخذ الخطوة الثانية إلا في حالة وجود تعارض فعلي مع الفهرس i ، وإلا فستضع x نفسه في A [i] ، لكن دعنا دعونا لا تقلق بشأن ذلك هنا.)

قل دالة هاش h hashes n عناصر S إلى الموقع i. لقد أثبتنا بالفعل (من خلال تحليل الطريقة 1) أنه يمكننا إيجاد h1 ، ... ، hN ، بحيث يكون إجمالي المساحة المستخدمة في الجداول الثانوية هو Pi (ni) 2. يبقى أن نظهر أنه يمكننا إيجاد دالة من المستوى الأول h بحيث Pi (ني) 2 = O (N). في الواقع ، سوف نعرض ما يلي:

Theorem 6. إذا اخترنا نقطة البداية h من المجموعة العالمية H ، إذن

Pr[X i (ni)2 > 4N] < 1/2. 

برهان. دعونا نثبت هذا من خلال إظهار أن E [Pi (ni) 2] <2N. هذا يعني ما نريد من عدم المساواة ماركوف. (إذا كان هناك احتمال حتى 1/2 بأن المبلغ يمكن أن يكون أكثر من 4N ، فإن هذه الحقيقة وحدها تعني أن التوقعات يجب أن تكون أكثر من 2N. وبالتالي ، إذا كان التوقع أقل من 2N ، فإن احتمال الفشل يجب أن يكون أقل 02/01).

الآن ، الحيلة الصعبة هي أن إحدى الطرق لحساب هذا المبلغ هي حساب عدد الأزواج المطلوبة التي لها تصادم ، بما في ذلك الاصطدامات مع الذات. على سبيل المثال ، إذا كانت السلة تحتوي على {d و e و f} ، فسيواجه d تعارضًا مع كل من {d و e و f} وسيواجه e تعارضًا مع كل من {d و e و f} وسيواجه f كل من {d ، e ، f} ، لذلك نحصل على 9. لذلك ، لدينا:

 E[X i (ni)2] = E[X x X y Cxy] (Cxy = 1 if x and y collide, else Cxy = 0) = N +X x X y6=x E[Cxy] ≤ N + N(N − 1)/M (where the 1/M comes from the definition of universal) < 2N. (since M = N) 

لذلك ، نحن فقط نحاول اختبار عشوائي h من H حتى نجد واحدًا مثل Pi n2 i <4N ، ومن ثم إصلاح هذه الوظيفة h ، نجد N دالة هاش ثانوية h1 ، ... ، hN كما في الطريقة الأولى.

6. مزيد من المناقشة

6.1 طريقة تجزئة عالمية أخرى

فيما يلي طريقة أخرى لإنشاء وظائف تجزئة عالمية ، والتي تكون أكثر كفاءة بقليل من طريقة المصفوفة المقدمة مسبقًا.

في طريقة المصفوفة ، اعتبرنا المفتاح متجهًا للبتات. في هذه الطريقة ، سنعتبر بدلاً من ذلك أن المفتاح x هو ناقل للأعداد الصحيحة [x1 ، x2 ، ... ، xk] مع الشرط الوحيد بأن يكون كل xi في النطاق {0 ، 1 ، ... ، M-1}. على سبيل المثال ، إذا كان لدينا سلاسل من الطول k ، فإن xi يمكن أن تكون الحرف ith (إذا كان حجم جدولنا 256 على الأقل) أو زوج ith من الأحرف (إذا كان حجم جدولنا هو 65536 على الأقل). بالإضافة إلى ذلك ، سوف نطلب أن يكون حجم طاولتنا M أولي. لتحديد دالة التجزئة h ، نختار k الأرقام العشوائية r1 و r2 و ... و pk من {0 ، 1 ، ... ، M - 1} ونحدد:

 h(x) = r1x1 + r2x2 + . . . + rkxk mod M. 

يتم إنشاء دليل على أن هذه الطريقة عالمية بنفس طريقة إثبات طريقة المصفوفة. اجعل x و y مفتاحين مختلفين. نريد أن نظهر أن Prh (h (x) = h (y)) ≤ 1 / M. منذ x! = Y ، يجب أن تكون هناك حالة عندما يكون هناك بعض الفهرس i بحيث xi! = Yi. الآن تخيل أنك حددت أولاً جميع الأرقام العشوائية rj لـ j! = I. دع h ′ (x) = Pj6 = i rjxj. لذلك ، باختيار ri ، نحصل على h (x) = h ′ (x) + rixi. هذا يعني أن لدينا تعارضًا بين x و y متى بالضبط

 h′(x) + rixi = h′(y) + riyi mod M, or equivalently when ri(xi − yi) = h′(y) − h′(x) mod M. 

بما أن M أولية ، فإن القسمة على قيمة غير صفرية من mod M صالحة (كل عدد صحيح من 1 إلى M −1 يحتوي على معامل معكوس المضاعف M) ، مما يعني أن هناك قيمة واحدة فقط ri modulo M والتي تحمل المعادلة أعلاه صحيح ، أي ri = (h ′ (y) - h ′ (x)) / (xi - yi) mod M. وبالتالي ، فإن احتمال وقوع هذا الحادث هو بالضبط 1 / M.

6.2 استخدامات أخرى للتجزئة

افترض أن لدينا سلسلة طويلة من العناصر ، ونريد أن نرى عدد العناصر المختلفة الموجودة في القائمة. هل هناك طريقة جيدة للقيام بذلك؟

تتمثل إحدى الطرق في إنشاء جدول تجزئة ، ثم المرور عبر التسلسل عن طريق إجراء بحث عن كل عنصر ثم إدخاله إذا لم يكن موجودًا بالفعل في الجدول. عدد العناصر الفردية هو ببساطة عدد الإدخالات.

والآن ، ماذا لو كانت القائمة ضخمة حقًا وليس لدينا مكان لتخزينها ، لكن الإجابة التقريبية مناسبة لنا. على سبيل المثال ، تخيل أننا جهاز توجيه ولاحظ عدد الحزم التي تمر ، ونريد (تقريبًا) معرفة عدد عناوين IP المصدر المختلفة الموجودة.

إليك فكرة جيدة: دعنا نقول أن لدينا دالة هاش h تتصرف كدالة عشوائية ، وعلينا أن نتخيل أن h (x) رقم حقيقي من 0 إلى 1. هناك شيء واحد يمكننا القيام به هو مجرد تتبع الحد الأدنى تم إنتاج قيمة التجزئة حتى الآن (لذلك لن يكون لدينا جدول على الإطلاق). على سبيل المثال ، إذا كانت المفاتيح 3،10،3،3،12،10،12 و h (3) = 0.4 ، h (10) = 0.2 ، h (12) = 0.7 ، فإننا نحصل على 0 ، 2.

الحقيقة هي أنه إذا حددنا N أرقام عشوائية في [0 ، 1] ، ستكون القيمة الدنيا المتوقعة 1 / (N + 1). بالإضافة إلى ذلك ، هناك فرصة جيدة أن تكون قريبة جدًا (يمكننا تحسين تقديرنا من خلال تشغيل العديد من وظائف التجزئة وأخذ الوسيط في المستويات المنخفضة).

السؤال: لماذا استخدام دالة التجزئة ، وليس فقط اختيار رقم عشوائي في كل مرة؟ هذا لأننا نهتم بعدد العناصر المختلفة ، وليس فقط العدد الإجمالي للعناصر (هذه المشكلة أبسط بكثير: مجرد استخدام عداد ...).

الأصدقاء ، هل كان هذا المقال مفيدًا لك؟ اكتب التعليقات وانضم إلى اليوم المفتوح ، الذي سيعقد في 25 أبريل.