مقدمة في أنظمة التشغيل

مرحبا يا هبر! أود أن ألفت انتباهكم إلى سلسلة من المقالات المترجمة لأدب واحد مثير للاهتمام في رأيي - OSTEP. تناقش هذه المقالة بعمق أعمال أنظمة التشغيل المشابهة لنظام التشغيل يونكس ، أي العمل مع العمليات ، وجداول المواعيد المختلفة ، والذاكرة ، والمكونات المماثلة الأخرى التي تشكل نظام التشغيل الحديث. الأصلي لجميع المواد التي يمكنك أن ترى هنا . يرجى ملاحظة أن الترجمة تمت بدون احتراف (بحرية تامة) ، لكن آمل أن أحتفظ بالمعنى العام.

يمكن العثور على العمل المختبري حول هذا الموضوع هنا:

أجزاء أخرى:

ويمكنك إلقاء نظرة على قناتي في برقية =)

مقدمة إلى المجدول

جوهر المشكلة: كيفية وضع سياسة مخطط
كيف ينبغي تطوير أطر سياسة الجدولة الأساسية؟ ما ينبغي أن يكون الافتراضات الرئيسية؟ ما المقاييس مهمة؟ ما التقنيات الأساسية المستخدمة في الحوسبة المبكرة؟

افتراضات عبء العمل

قبل مناقشة السياسات المحتملة ، لبداية ، سنقوم ببضع استطرادات مبسطة حول العمليات الجارية في النظام ، والتي تسمى مجتمعة عبء العمل . من خلال تحديد عبء العمل باعتباره جزءًا مهمًا من سياسات البناء وكلما زادت معرفتك بحجم العمل ، كانت السياسة الأفضل التي يمكنك كتابتها.

نحن نضع الافتراضات التالية حول العمليات الجارية في النظام ، والتي تسمى أحيانًا الوظائف (المهام). جميع هذه الافتراضات تقريبًا ليست واقعية ، ولكنها ضرورية لتطوير الفكر.

كل مهمة تدير نفس القدر من الوقت ،
يتم تعيين جميع المهام في نفس الوقت ،
المهمة في متناول اليد حتى الانتهاء ،
جميع المهام تستخدم فقط وحدة المعالجة المركزية ،
وقت التشغيل لكل مهمة معروف.

مقاييس الجدولة

بالإضافة إلى بعض الافتراضات المتعلقة بالتحميل ، فأنت بحاجة إلى أداة أخرى لمقارنة سياسات التخطيط المختلفة: مقاييس المجدول. المقياس هو مجرد مقياس لشيء ما. هناك عدد من المقاييس التي يمكن استخدامها لمقارنة المخططين.

على سبيل المثال ، سوف نستخدم مقياسًا يسمى وقت التحويل. يتم تعريف وقت الدوران للمهمة على أنه الفرق بين الوقت المستغرق لإكمال المهمة والوقت الذي تدخل فيه المهمة في النظام.

Tturnaround = Tcompletion - Tarrival

منذ افترضنا أن جميع المهام وصلت في نفس الوقت ، ثم Ta = 0 وبالتالي Tt = Tc. ستتغير هذه القيمة بشكل طبيعي عندما نغير الافتراضات المذكورة أعلاه.

متري آخر هو الإنصاف (الإنصاف ، الصدق). غالبًا ما تعارض الإنتاجية والصدق خصائص التخطيط. على سبيل المثال ، قد يقوم برنامج الجدولة بتحسين الأداء ، ولكن على حساب انتظار مهام أخرى ، مما يقلل من النزاهة.

أول في أول من (FIFO)

الخوارزمية الأساسية التي يمكننا تنفيذها تسمى FIFO أو تأتي أولاً (في) ، وتخدم أولاً (خارج) . تتمتع هذه الخوارزمية بالعديد من المزايا: إنها سهلة التنفيذ وتناسب جميع افتراضاتنا ، وتؤدي المهمة بشكل جيد.

النظر في مثال بسيط. افترض أنه تم تعيين 3 مهام في نفس الوقت. لكن لنفترض أن المهمة (أ) جاءت قبل ذلك بقليل عن أي شخص آخر ، لذلك ستكون في قائمة التنفيذ قبل الأخرى ، تمامًا مثل B بالنسبة إلى C. افترض أن كل منهما يستغرق 10 ثوانٍ لإكماله. ماذا سيكون متوسط الوقت لاستكمال هذه المهام؟

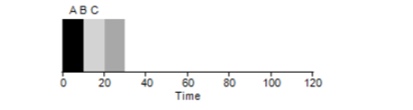
عد القيم - 10 + 20 + 30 والقسمة على 3 ، نحصل على متوسط وقت تنفيذ البرنامج يساوي 20 ثانية.

الآن دعونا نحاول تغيير افتراضاتنا. على وجه الخصوص ، الافتراض 1 ، وبالتالي فإننا لن نفترض بعد الآن أن كل مهمة تأخذ نفس القدر من الوقت. كيف سوف تظهر FIFO نفسها هذه المرة؟

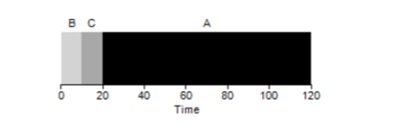
كما اتضح ، فإن أوقات التنفيذ المختلفة للمهام لها تأثير سلبي للغاية على إنتاجية خوارزمية FIFO. افترض أن المهمة A سيتم تنفيذها لمدة 100 ثانية ، في حين أن B و C ستبقى 10 لكل منهما.

كما يتضح من الشكل ، فإن متوسط وقت النظام هو (100 + 110 + 120) / 3 = 110. يسمى هذا التأثير بتأثير القافلة ، عندما يكون بعض المستهلكين على المدى القصير لمورد ما في خط بعد مستهلك كثيف. يبدو وكأنه خط بقالة عندما يكون هناك عميل لديه عربة كاملة أمامك. أفضل حل للمشكلة هو محاولة تغيير أمين الصندوق أو الاسترخاء والتنفس بعمق.

أقصر وظيفة أولا

هل من الممكن حل موقف مماثل بطريقة أو بأخرى مع العمليات الثقيلة؟ بالطبع يسمى نوع آخر من الجدولة Shortest Job First (SJF). خوارزمية لها هي أيضا بدائية للغاية - كما يوحي الاسم ، سيتم تشغيل أقصر المهام واحدا تلو الآخر.

في هذا المثال ، ستكون نتيجة البدء في نفس العمليات تحسناً في متوسط وقت التشغيل للبرامج وسيكون 50 بدلاً من 110 ، وهو أفضل مرتين تقريبًا.

وبالتالي ، على افتراض أن جميع المهام تصل في نفس الوقت ، يبدو أن خوارزمية SJF هي الخوارزمية المثلى. ومع ذلك ، فإن افتراضاتنا لا تزال غير واقعية. هذه المرة ، نغير الافتراض 2 ونتخيل هذه المرة أن المهام يمكن أن تبقى في أي وقت ، وليس جميعها في نفس الوقت. ما هي المشاكل التي يمكن أن يؤدي هذا إلى؟

تخيل أن المهمة A (100s) تصل أولاً وتبدأ تنفيذها. في الوقت t = 10 ، تصل المهام B ، C ، كل منها سيستغرق 10 ثوانٍ. وبالتالي ، فإن متوسط وقت التنفيذ هو (100+ (110-10) + (120-10)) \ 3 = 103. ماذا يمكن للمخطط أن يفعله لتحسين الوضع؟

أقصر وقت للإنجاز أولاً (STCF)

من أجل تحسين الموقف ، نتجاهل الافتراض 3 بأن البرنامج قيد التشغيل وحتى الانتهاء. بالإضافة إلى ذلك ، سنحتاج إلى دعم الأجهزة ، وكما قد تفكر ، سنستخدم مؤقتًا لمقاطعة مهمة العمل وتبديل السياقات . وبالتالي ، يمكن لجدولة القيام بشيء ما في الوقت الذي تصل فيه المهام B و C - إيقاف تنفيذ المهمة A ووضع المهام B و C في المعالجة ، وبعد الانتهاء ، تابع العملية A. يسمى هذا المجدول STCF أو Preemptive Job First .

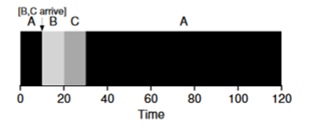
ستكون نتيجة هذا المجدول هي هذه النتيجة: ((120-0) + (20-10) + (30-10)) / 3 = 50. وبالتالي ، يصبح هذا المجدول أكثر ملاءمة لمهامنا.

زمن الاستجابة المترية

وبالتالي ، إذا عرفنا وقت تشغيل المهام وأن هذه المهام تستخدم وحدة المعالجة المركزية فقط ، فسيكون STCF هو الحل الأفضل. ومرة واحدة في الأيام الأولى ، عملت هذه الخوارزميات بشكل جيد. ومع ذلك ، الآن يقضي المستخدم معظم الوقت في الجهاز ويتوقع تفاعلًا تفاعليًا مثمرًا منه. لذلك تم إنشاء مقياس جديد - زمن الاستجابة (الاستجابة).

يتم حساب وقت الاستجابة على النحو التالي:

Tresponse = Tfirstrun - تريفال

وبالتالي ، على سبيل المثال السابق ، سيكون وقت الاستجابة على النحو التالي: A = 0 ، B = 0 ، B = 10 (abg = 3.33).

واتضح أن خوارزمية STCF ليست جيدة في الموقف عندما تصل 3 مهام في نفس الوقت - سيتعين عليها الانتظار حتى يتم الانتهاء من المهام الصغيرة تمامًا. وبالتالي ، فإن الخوارزمية جيدة لقياس وقت التحول ، ولكنها سيئة بالنسبة لقياس التفاعل. تخيل أنك جالس على الجهاز في محاولة لكتابة أحرف في المحرر ، يجب عليك الانتظار أكثر من 10 ثوان ، لأن بعض المهام الأخرى يشغلها المعالج. هذا ليس لطيفا جدا.

إذن نحن نواجه مشكلة أخرى - كيف يمكننا بناء مجدول حساس لوقت الاستجابة؟

جولة روبن

لحل هذه المشكلة ، تم تطوير خوارزمية Round Robin (RR). الفكرة الأساسية بسيطة للغاية: بدلاً من بدء المهام لإكمال الإكمال ، سنبدأ المهمة لفترة زمنية معينة (تسمى كمية الوقت) ثم ننتقل إلى مهمة أخرى من قائمة الانتظار. الخوارزمية تكرر عملها حتى يتم الانتهاء من جميع المهام. في هذه الحالة ، يجب أن يكون وقت تشغيل البرنامج مضاعفًا للوقت الذي يقطع فيه الموقت العملية. على سبيل المثال ، إذا كان المؤقت يقطع العملية كل x = 10 مللي ثانية ، فيجب أن يكون حجم نافذة تنفيذ العملية مضاعفات 10 ويكون 10.20 أو x * 10.

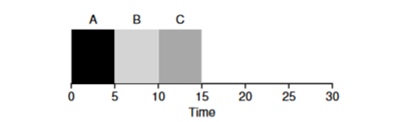
دعونا نلقي نظرة على مثال: تصل مهام ABV في وقت واحد إلى النظام ويريد كل منهم العمل لمدة 5 ثوان. ستكمل خوارزمية SJF كل مهمة حتى النهاية قبل بدء أخرى. في المقابل ، ستعمل خوارزمية RR مع نافذة الإطلاق = 1 ثانية على تنفيذ المهام على النحو التالي (الشكل 4.3):

(SJF مرة أخرى (سيئة لوقت الاستجابة)

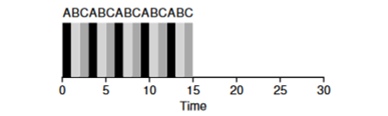(جولة روبن (جيد لوقت الاستجابة)

متوسط وقت الاستجابة للخوارزمية هو RR (0 + 1 + 2) / 3 = 1 ، بينما بالنسبة لـ SJF (0 + 5 + 10) / 3 = 5.

من المنطقي أن نفترض أن نافذة الوقت هي معلمة مهمة للغاية بالنسبة للوائح الراديو ، كلما كان حجمها أصغر ، كلما زاد زمن الاستجابة. ومع ذلك ، لا يمكنك جعلها صغيرة جدًا ، لأن وقت تبديل السياق سوف يلعب أيضًا دورًا في الأداء العام. وبالتالي ، يتم تعيين توقيت نافذة التنفيذ من قبل مهندس نظام التشغيل ويعتمد على المهام المخطط تنفيذها في ذلك. لا يعد تبديل السياق عملية الخدمة الوحيدة التي تقضي الوقت - فالبرنامج قيد التشغيل يعمل أكثر من ذلك بكثير ، على سبيل المثال ، العديد من ذاكرات التخزين المؤقت ، وفي كل مرة يكون من الضروري حفظ هذه البيئة واستعادتها ، والتي قد تستغرق أيضًا الكثير من الوقت.

RR هو مخطط كبير إذا كان فقط متري وقت الاستجابة. لكن كيف سيكون سلوك وقت المهمة للمهمة مع هذه الخوارزمية؟ النظر في المثال أعلاه ، عندما وقت التشغيل A ، B ، C = 5s والوصول في نفس الوقت. ستنتهي المهمة "أ" في 13 و "ب" في 14 و "ج" في 15s و متوسط وقت الدوران هو 14s. وبالتالي ، RR هي أسوأ خوارزمية لمقاييس دوران.

بعبارات أعم ، أي خوارزمية مثل RR صادقة ، تقسم وقت التشغيل على وحدة المعالجة المركزية بالتساوي بين جميع العمليات. وبالتالي ، تتعارض هذه المقاييس باستمرار مع بعضها البعض.

وبالتالي ، لدينا العديد من الخوارزميات المتعارضة وفي الوقت نفسه تبقى العديد من الافتراضات - أن وقت المهمة معروف وأن المهمة تستخدم وحدة المعالجة المركزية فقط.

خلط مع I / O

بادئ ذي بدء ، نزيل الافتراض 4 بأن العملية تستخدم وحدة المعالجة المركزية فقط ، بالطبع هذا ليس كذلك ، ويمكن أن تتحول العمليات إلى معدات أخرى.

في اللحظة التي تتطلب فيها عملية ما عملية إدخال / إخراج ، تنتقل العملية إلى حالة محظورة ، في انتظار إكمال عملية الإدخال / الإخراج. إذا تم إرسال I / O إلى القرص الثابت ، فقد تستغرق هذه العملية ما يصل إلى عدة مللي ثانية أو أكثر ، وسيكون المعالج خاملاً في تلك اللحظة. في هذا الوقت ، قد يستولي المجدول على المعالج بأي عملية أخرى. القرار التالي الذي سيتعين على المجدول اتخاذه هو عندما تكمل العملية I / O. عندما يحدث هذا ، ستحدث مقاطعة وسيقوم نظام التشغيل بوضع عملية I / O-call في حالة الاستعداد.

النظر في مثال على العديد من المهام. كل واحد منهم يحتاج إلى 50 مللي ثانية من وقت المعالج. ومع ذلك ، فإن أول واحد سوف يصل إلى I / O كل 10ms (والتي سيتم تنفيذها أيضا لمدة 10ms). وتستخدم العملية B ببساطة معالج 50 مللي ثانية بدون الإدخال / الإخراج.

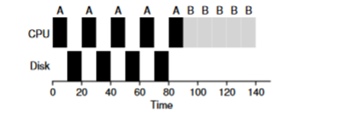
في هذا المثال ، سوف نستخدم جدولة STCF. كيف يتصرف المجدول إذا قمت بتشغيل عملية مثل A على ذلك؟ سوف يستمر كما يلي - أولاً ، العملية بالكامل A ، ثم العملية B.

تتمثل الطريقة التقليدية لحل هذه المشكلة في ترجمة كل مهمة فرعية من العملية A تبلغ 10 مللي ثانية كمهمة منفصلة. وبالتالي ، عند البدء بخوارزمية STJF ، يكون الاختيار بين مهمة 50 ms ومهمة ms 10 واضحًا. ثم ، عند اكتمال المهمة الفرعية A ، سيتم بدء العملية B و I / O. بعد اكتمال الإدخال / الإخراج ، سيكون من المعتاد بدء عملية 10 مللي ثانية مرة أخرى بدلاً من العملية ب. وبالتالي ، من الممكن إدراك التداخل عند استخدام وحدة المعالجة المركزية بواسطة عملية أخرى أثناء انتظار أول إدخال / إخراج. ونتيجة لذلك ، يتم استخدام النظام بشكل أفضل - في وقت تنتظر فيه العمليات التفاعلية I / O ، يمكن تنفيذ عمليات أخرى على المعالج.

أوراكل لم يعد

الآن دعنا نحاول التخلص من الافتراض بأن وقت المهمة معروف. هذا هو افتراض الأسوأ والأكثر واقعية من القائمة بأكملها. في الواقع ، في أنظمة التشغيل القياسية المتوسطة ، لا يعرف نظام التشغيل نفسه سوى القليل جدًا عن الوقت الذي يستغرقه لإكمال المهام ، فكيف يمكنك إنشاء مجدول دون معرفة المدة التي ستستغرقها المهمة؟ ربما يمكننا استخدام بعض مبادئ لوائح الراديو لحل هذه المشكلة؟

يؤدي

درسنا الأفكار الأساسية لتخطيط المهام واستعرضنا عائلتين من المخططين. أول واحد يبدأ أقصر مهمة في البداية ، وبالتالي يزيد من وقت الدوران ، والثانية ممزقة بين جميع المهام على قدم المساواة ، مما يزيد من زمن الاستجابة. كلتا الخوارزميات سيئة حيث الخوارزميات العائلية الأخرى جيدة. درسنا أيضًا كيف يمكن أن يؤدي الاستخدام المتوازي لوحدة المعالجة المركزية (CPU) و I / O إلى تحسين الأداء ، ولكن لا يزال لا يحل المشكلة مع استبصار نظام التشغيل. وفي الدرس التالي ، سنعتبر مخططًا يبحث في الماضي القريب ويحاول التنبؤ بالمستقبل. ويسمى قائمة انتظار ردود الفعل متعددة المستويات.

أنظمة التشغيل: ثلاث قطع سهلة. الجزء 4: مقدمة إلى المجدول (الترجمة)