🧛🏾 👨‍💼 🤚🏿 لكن ألا نلوح بالاتصال البصري؟ الليزر ، الفضاء ، CubeSat 🕦 🤜 👹

المواد الموضحة أدناه هي نتيجة للعمل المشترك مع معلمي TU Ilmenau كجزء من مشروع دورة محلية (مشروع بحث متقدم). تجربة مثيرة للاهتمام ، ولكن ليس من دون بعض الصعوبات. لقد قمنا بهذا المشروع (وواحد آخر) برفيقي في ذلك الوقت - نعم ، ولذا فقد كنا محظوظين للدراسة معًا والذهاب إلى ألمانيا. في الحقيقة ، كانت هي التي قامت بهذا الجزء من العمل إلى حد كبير ، لكنني أريد نشر هذا الموضوع.

لذلك ، في أحد الأيام حددنا موعدًا لاختيار موضوع للعمل العلمي ...

خلفية قصيرة (في الوجوه)

مدرس اللغة الألمانية رقم 1 : أوه ، سمعت أنك تدرس أقمار CubeSat هناك في المنزل؟

أنا وزوجتي المستقبلية : حسنًا ، يمكنك قول ذلك ...

تسوية رقم 1 : عظيم! ولكن ماذا لو حاولت النظر في الاتصال البصري بين الأقمار الصناعية؟ أعلم أن البصريات تقدم في بعض الحالات أفضل أداء للطاقة ، وبالنسبة لهذه الأقمار الصناعية الصغيرة ، أفترض أن هذه المشكلة مهمة للغاية. لديّ صديق واحد يشارك مهنيًا في البصريات اللاسلكية. أعتقد أنه سيكون مشروعًا مثيرًا للاهتمام!

نحن : أصوات مثيرة للاهتمام!

(يمر بعض الوقت)

لقاء مع مدرس ألماني رقم 2 .

تسوية رقم 2 : نعم ، كل هذا ، بالطبع ، شيء عظيم ، ولكن أي نوع من الأقمار الصناعية؟ هذه كتلة صغيرة؟ هل يمكنهم التواصل؟ من اقترح هذا؟ فهمت ... على ما يبدو ، لن نراه في هذه الاجتماعات. ابحث عن أمثلة من العالم الحقيقي - لا أصدق حتى الآن.

وانطلقنا ...

ولفرحهم ، وجدوا حتى مقالة كاملة مكرسة لهذا الموضوع. كان الفرق المهم هو أن التواصل من خلال البصريات كان من المفترض أن يكون مع الأرض ، وليس بين الأقمار الصناعية. هذا مهم جدا لأنه:

جميع أنواع الانتثار والتدخل ، بالطبع ، في هذه الحالة أكثر ،
ومع ذلك ، يمكن تعيين جهاز الاستقبال على الأرض بشكل كبير بما فيه الكفاية ، وجهاز الإرسال دقيق للغاية. وقطاع الفضاء ، كما تعلمون ، يعقد الأمور قليلاً.

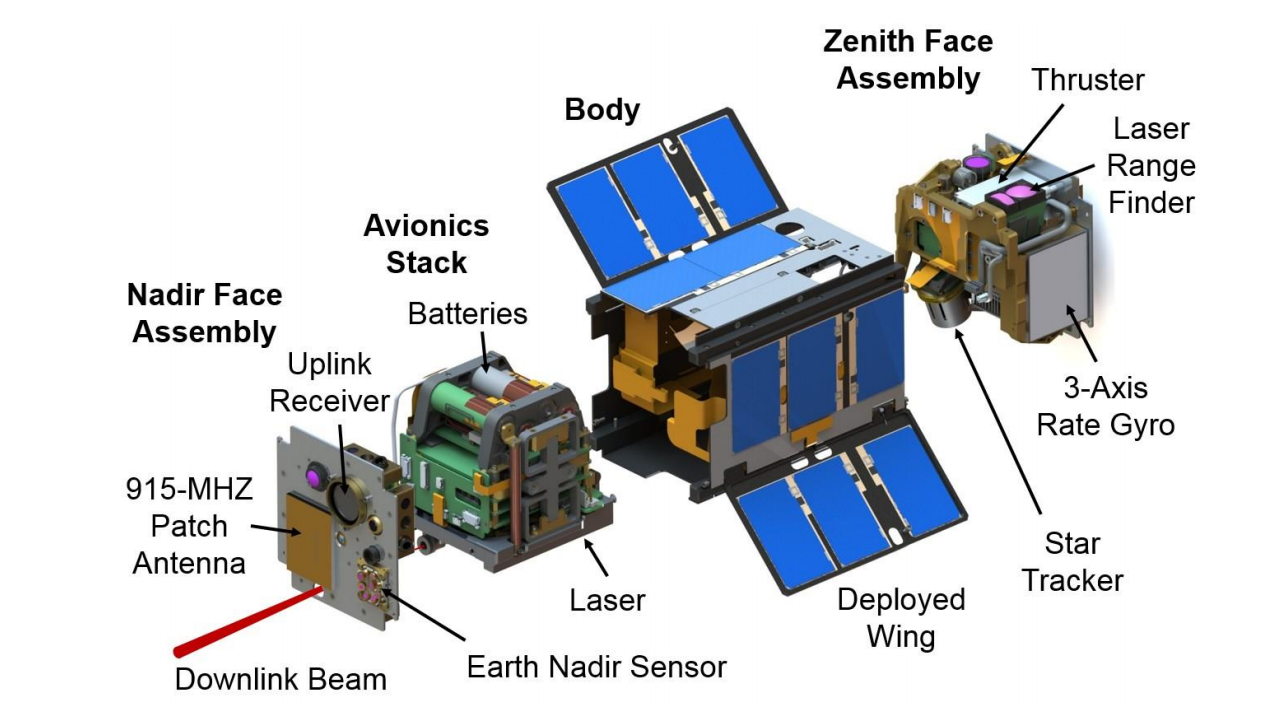
التين. 1. تمثيل تخطيطي للأقمار الصناعية النانوية AeroCube-OCSD [1].

لكن هذا كان شيئًا بالفعل ، وحددنا موعدًا مرة أخرى.

تسوية رقم 2 : حسنًا ، حسنًا ، منذ ناسا ... دعونا نحاول حساب ميزانية الطاقة ومقارنتها بميزانية الطاقة للرابط اللاسلكي. مقالات ذات صلة للتخلص؟

وألقى مقالته [2] (سأشير إليها عدة مرات اليوم) ومقالتين لكتاب آخرين لفهم القضية بشكل عام.

ماذا تعني ميزانية الطاقة للخط البصري بين الأقمار الصناعية؟

ميزانية الطاقة الضوئية اللاسلكية

ولكنه يعني بحد ذاته ، بشكل عام ، نفس الشيء كالمعتاد (قدرة المرسل اللازمة ، القدرة المستقبلة ، SNR ، إلخ.) - تعتبر الضوضاء فقط أكثر إثارة للاهتمام مما هي عليه في حالة الاتصالات اللاسلكية ...

لنبدأ في وضع النماذج - سيكون الأمر أكثر وضوحًا:

import numpy as np from matplotlib.pyplot import plot, grid, xlabel, ylabel, legend import matplotlib.pyplot as plt from scipy import special

لنفترض أن لدينا مثل هذا النظام:

 #initial parameters for optical case R = 100*1e3 #distance between objects, eg satellites, in m (100 km) Bit_rate = 1e6 #bit rate (1 Mbps) h = 6.62607004*1e-34 # Planck constant c = 299792458 #speed of light wavelength_opt = 1550*1e-9 #optical wavelength freq_opt = c/wavelength_opt #optical frequency Ptx_opt = 1 #transmitter power in Watts Ptx_opt_dBm = 10*np.log10(Ptx_opt*1e3) #transmitter power in dBm

نحدد مجموعة معينة من الأقطار الممكنة لأجهزة الاستقبال البصرية (في الواقع ، العدسات) - نضع في الاعتبار القيود المفروضة على حجم الأقمار الصناعية نفسها:

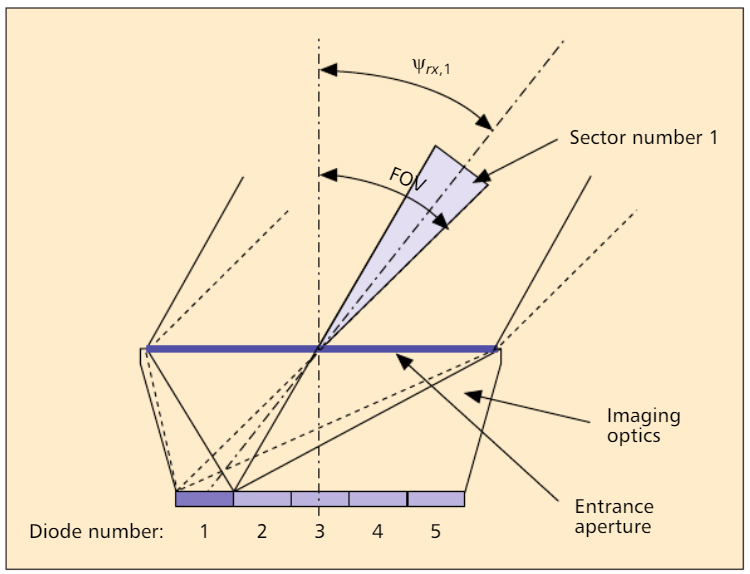
 a = [i for i in range(0,50,5)] a = np.array(a)*1e-3 #diameter of the receiver (in meters) a[0] = 1*1e-3 a_m = a*100 # for figures (in cm)

الشكل 2. رسم تخطيطي للكاشف الضوئي: يظهر كمثال للقطاع رقم 1 ، حيث يتم عرض زوايا حدوثه على الثنائي الضوئي رقم 1 [2].

وبعض زوايا الاختلاف المحتملة لشعاع الليزر (جهاز إرسالنا):

 div_ang = [0.2*1e-3, 0.5*1e-3, 2*1e-3, 5*1e-3, 7*1e-3] div_ang = np.array(div_ang) #half of divergence angle

التين. 3. توضيح زاوية الاختلاف في شعاع الليزر.

يمكن حساب القدرة عند دخل المستقبِل (القدرة المستقبلة) بالصيغة [2] :

$P_ {rx} = \ frac {A_ {rx}} {2 \ pi R ^ 2} \ left (1 - \ frac {ln2} {ln (cos \ theta_ {div})} \ right) P_ {tx} \ رباعية [ث]$

حيث $A_ {rx} = \ frac {d_ {rx} ^ 2 \ pi} {4}$ هي منطقة الاستقبال ، $d_ {rx}$ - قطر العدسة المستقبلة ، $R$ - المسافة بين الأقمار الصناعية ، $\ theta_ {div}$ هو نصف زاوية الاختلاف و $P_ {tx}$ - الطاقة المنقولة.

 Prx_opt_dBm = np.zeros((len(div_ang), len(a))) Prx_opt = np.zeros((len(div_ang), len(a))) Pathloss_dBm = np.zeros((len(div_ang), len(a))) Pathloss = np.zeros((len(div_ang), len(a))) Arx_m2 = (np.pi/4)*(a**2) for f, dvangl in enumerate(div_ang): #received power Prx_opt[f,:] = (Ptx_opt*Arx_m2)/ (2*np.pi*(R**2))\ *(1-(np.log(2)/np.log(np.cos(dvangl)))) Prx_opt_dBm[f,:] = 10*np.log10(Prx_opt[f,:]*1e3) #path loss Pathloss[f,:] = (Arx_m2)/(2*np.pi*(R**2))\ *(1-(np.log(2)/np.log(np.cos(dvangl)))) Pathloss_dBm[f,:] = 10*np.log10(Pathloss[f,:]*1000)

حسنا ، هناك شيء بالفعل هناك. ولكن كم هو كل هذا يمكن تحقيقه جسديا؟

حدود الحساسية

حدود الكم

أذكر صيغة طاقة الفوتون:

$E = hf \ quad \ left [m ^ 2 kg / s ^ 2 \ right]$

حيث $ح$ = 6.62607004e-34 $م ^ 2 كجم / ثانية$ هو ثابت بلانك ، و $و$ - تردد الموجة الحاملة (Hz).

وسيتبع ذلك ارشادي صغير مستمد من مشاوراتنا. إذا كان هناك من يعرف مبررًا أو دحضًا نظريًا - فيرجى مشاركته!

الطاقة المطلوبة (الحد الأدنى من الطاقة لكل بت من المعلومات على جانب جهاز الاستقبال لاكتشاف شيء على الأقل):

$E_ {req، Q} = N_ {ph} hf \ quad \ left [m ^ 2 kg / s ^ 2 \ right]$

حيث $N_ {ph}$ - متوسط عدد الفوتونات اللازمة للكشف عن 1 بت من المعلومات.

الطاقة النظرية للنبض البصري:

 E_theor = 10*h*freq_opt

قيمة طاقة أكثر واقعية للنبض البصري (صمام ثنائي APD ):

 E_real_APD = 1000*h*freq_opt

قيمة طاقة أكثر واقعية للنبض البصري ( PIN diode):

 E_real_PIN = 10000*h*freq_opt

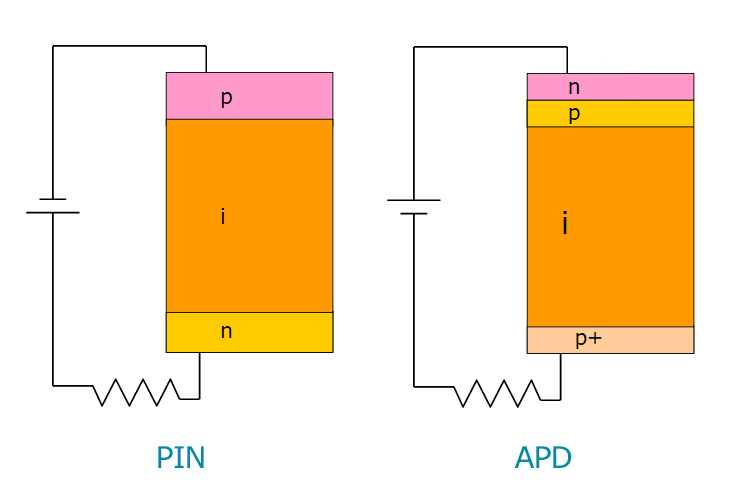
الشكل 4. دائرة الثنائيات الضوئية قيد الدراسة.

مطلوب (الحد الأدنى) قوة الاستقبال (الحساسية القصوى):

$P_ {req، Q} = 10 \ log_ {10} \ left (\ frac {E_ {req، Q} B} {10 ^ {- 3}} \ right) = 10 \ log_ {10} \ left (\ frac {E_ {req، Q} R_b} {10 ^ {- 3}} \ right) \ quad [dBm]$

حيث $B$ هو عرض النطاق الترددي لقناة الاتصال ، و $R_b$ هو معدل البت.

 P_req_theor = 10*np.log10(E_theor*Bit_rate*1000) P_req_real_APD = 10*np.log10(E_real_APD*Bit_rate*1000) P_req_real_PIN = 10*np.log10(E_real_PIN*Bit_rate*1000)

ولكن هذا ليس كل شيء: التعديل يساهم أيضًا في الحد من المساهمة.

حدود احتمال الخطأ

كنقطة انطلاق ، سننظر في تعديل OOK (تشغيل وإيقاف التشغيل).

الشكل 5. توضيح لمبدأ تعديل OOK.

سيكون احتمال حدوث أخطاء ( BER ) هو [2]:

$P_b = \ frac {1} {2} ercf \ left (\ sqrt {\ frac {SNR} {2}} \ right) = \ frac {1} {2} ercf \ left (\ sqrt {\ frac {P_ { ةداملا مسا} ^ 2 \ gamma ^ 2} {2 \ sigma ^ 2}} \ right)$

حيث $SNR$ هي نسبة الإشارة إلى الضوضاء ، $\ سيغما ^ 2$ هو التباين في الضوضاء (أي قوة الضوضاء) ، و $\ جاما$ هي حساسية الثنائيات الضوئية ( استجابة الثنائي الضوئي ).

BER for OOK (PIN diode):

$P_ {b، PIN} = \ frac {1} {2} ercf \ left (\ frac {\ gamma P_ {req، PIN}} {\ sqrt {2 \ sigma_ {PIN} ^ 2}} \ right)$

وبالتالي:

$P_ {req، PIN} = \ frac {erfcinv (2P_b) \ sqrt {2 \ sigma_ {PIN} ^ 2}} {\ gamma} \ quad [W]$

BER for OOK (APD diode):

$P_ {b، APD} = \ frac {1} {2} ercf \ left (\ frac {\ gamma M P_ {req، APD}} {\ sqrt {2 \ sigma_ {APD} ^ 2}} \ right)$

وبالتالي:

$P_ {req، APD} = \ frac {erfcinv (2P_b) \ sqrt {2 \ sigma_ {APD} ^ 2}} {\ gamma M} \ quad [W]$

حيث $M$ - هذا هو بعض المكاسب المرجعية.

قوة الضوضاء

كما كنت قد خمنت ، سيتم أيضًا حساب الضوضاء بشكل مختلف قليلاً.

قوة الضوضاء ل PIN ديود

يمكن حساب الضوضاء الحرارية بالصيغة [3 ، صفحة 11] :

$\ sigma_ {PIN} ^ 2 = \ left (\ frac {4kT} {R_f} + 2qI_ {BE} \ right) I_2R_b = N_0 + 2qI_ {BE} I_2R_b \ quad [W]$

حيث $T = 290 ك$ . $ك = 1.38064852e-23$ - بولتزمان ثابت $R_f = \ frac {100} {2 \ pi C_d R_b}$ - المقاومة المباشرة $C_d$ - قدرة الثنائي الضوئي ، $ف$ هي شحنة الإلكترون ، $I_ {BE} = \ frac {I_C} {\ beta}$ - تيار الباعث الأساسي (باعث القاعدة أو تيار التسرب أو التيار المتحيز ) ، $I_2$ - قيمة Personick متكاملة (- أستسلم ، لم أجد ترجمة مناسبة ، من فضلك أخبرني) عن الضوضاء الحرارية $R_b$ - معدل بت $N_0$ - الكثافة الطيفية للضوضاء.

 Cd = 2*1e-12 #capacitance of the photodiode T = 290 #absolute temperature Rf = 100/(Cd*2*np.pi*Bit_rate) #photodiode resistance k = 1.38064852*1e-23 #Bolzman constant I2 = 0.562 #depends on filter (Personick integral) for match filter q = 1.60217662*1e-19 #electron charge Ibe = (0.25*1e-3)/200 #RESULT thermal_Noise_variance_add = 2*q*Ibe*I2*Bit_rate N_0 = 4*k*T/Rf #thermal noise density for PIN thermal_Noise_variance = N_0*Bit_rate*I2

قوة الضوضاء لل APD ديود

الاستعداد لهذا الصمام الثنائي - العديد من الحروف اللاتينية:

$\ sigma_ {APD} ^ 2 = \ frac {4kT} {R_f} I_2R_b + 2qI_dM_ {Si} ^ 2F_ {Si} I_2R_b = N_0 + 2qI_2R_b (I_ {BE} + M_ {Si} ^ 2F_ {Si} I_d) \ تقريبًا N_0 + 2qI_2I_dR_bM_ {Si} ^ 2F_ {Si} \ quad [W]$

حيث $I_d$ - التيار المظلم (التيار المظلم) ، $M_ {Si}$ هو مكسب نموذجي (السيليكون) ، $F_ {Si}$ - عامل الضوضاء الزائدة.

يتم استخلاص المعلمات مما يلي:

في هذه الورقة ، لا تؤخذ في الاعتبار ضوضاء ترانزستور تأثير حقل الإدخال (ضوضاء إدخال FET) وضوضاء تحميل ترانزستور تأثير حقل الإدخال (ضجيج حمل إدخال FET). اقرأ المزيد عن هذه الشروط في [3 ، صفحة 15] .

 Id = 0.05*10e-9 #dark current (500e-12) M_Si = 100 #typical gain F_Si = 7.9 #excess noise factor apd_noise_Si = 2*q*Id*I2*Bit_rate*(M_Si**2)*F_Si #noise

تصميم

تلقى السلطة

نحن نستبدل كل شيء موضح في صيغنا:

 r = 0.53 #A/W photodiode responsivity Pb = 10e-9 #Bit error rate (BER) P_req_pin = 10*np.log10((special.erfcinv(2*Pb)* np.sqrt(2*(thermal_Noise_variance+thermal_Noise_variance_add))/(r))*1e3) #in dBm P_req_apd_lin = special.erfcinv(2*Pb)*np.sqrt(2*(thermal_Noise_variance+apd_noise_Si))/(r*M_Si) P_req_apd = 10*np.log10(P_req_apd_lin*1e3) #in dBm fig = plt.figure(figsize=(10, 7), dpi=300) req_theor = np.ones((len(a_m),))*P_req_theor req_real_APD = np.ones((len(a_m),))*P_req_real_APD req_real_PIN = np.ones((len(a_m),))*P_req_real_PIN PIN = np.ones((len(a_m),))*P_req_pin APD = np.ones((len(a_m),))*P_req_apd a_m = a_m.reshape((10,)) plot(a_m, Prx_opt_dBm[0,:],'-o', label = '0.2 mrad') plot(a_m, Prx_opt_dBm[1,:],'-o', label = '0.5 mrad') plot(a_m, Prx_opt_dBm[2,:],'-o', label = '2 mrad') plot(a_m, Prx_opt_dBm[3,:],'-o', label = '5 mrad') plot(a_m, Prx_opt_dBm[4,:],'-o', label = '7 mrad') plot(a_m, req_theor,'k--', label = 'Sensitivity limit (theory)') plot(a_m, req_real_APD, '--*', label = 'Sensitivity limit (APD)') plot(a_m, req_real_PIN, '--', label = 'Sensitivity limit (PIN)') plot(a_m, APD, '-*',label = '1e-9 OOK BER limit (APD)') plot(a_m, PIN, label = '1e-9 OOK BER limit (PIN)') plt.gca().invert_yaxis() xlabel('Rx diameter (cm)'); ylabel('Prx and Preq (dBm)') legend() grid() plt.show()

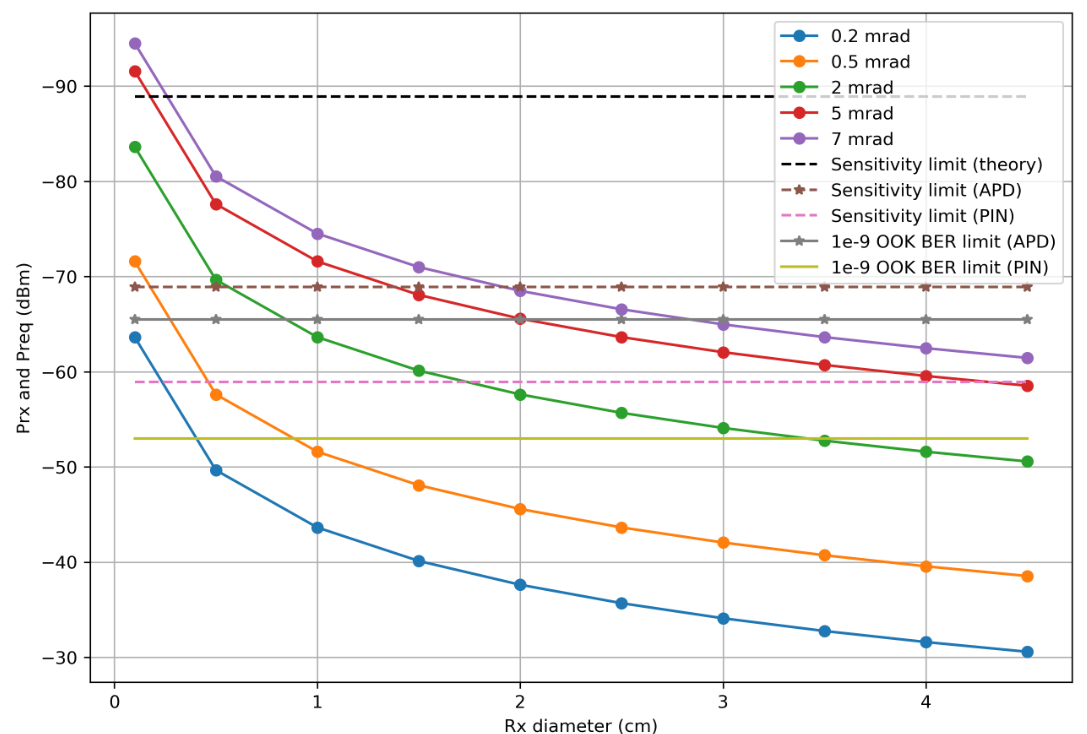
دعنا نوضح: تحتاج إلى إلقاء نظرة على تلك الأجزاء من المنحنيات التي تقع أسفل الخطوط الأفقية المقابلة.

السلطة المنقولة

والآن ، لنلقِ نظرة على المشكلة المعاكسة: نصلح بعض الطاقة على جانب الاستقبال ونرى نوع القوة التي ستحتاج إلى تطبيقها على جانب الإرسال:

$P_ {tx، dBm} = P_ {rx، dBm} + | L | + | L_ {إضافة} |$

حيث $L = 10 \ log_ {10} \ left [\ frac {A_ {rx}} {2 \ pi R ^ 2} \ left (1 - \ frac {ln2} {ln (cos \ theta_ {div})} \ right ) \ اليمين]$ هو توهين المسار ، و $L_ {add}$ - هذا هو بعض الهامش للخسائر.

 Prx_req_dB_APD = -65.5 Prx_req_dB_PIN = -52.9 margin = 5 Arx_m2 = np.zeros((len(a))) Ptx_variable_APD = np.zeros((len(div_ang), len(a))) Ptx_variable_PIN = np.zeros((len(div_ang), len(a))) #area rx Arx_m2 = (np.pi/4)*(a**2) for f, dvangl in enumerate(div_ang): #Ptx required Ptx_variable_APD[f,:] = Prx_req_dB_APD + np.abs(Pathloss_dBm[f,:]) + margin; Ptx_variable_PIN[f,:] = Prx_req_dB_PIN + np.abs(Pathloss_dBm[f,:]) + margin; fig = plt.figure(figsize=(10, 7), dpi=300) plot(a_m, Ptx_variable_APD[0,:],'-o', label = 'APD, 0.2 mrad') plot(a_m, Ptx_variable_PIN[0,:],'-*', label = 'PIN, 0.2 mrad') plot(a_m, Ptx_variable_APD[1,:],'-o', label = 'APD, 0.5 mrad') plot(a_m, Ptx_variable_PIN[1,:],'-*', label = 'PIN, 0.5 mrad') plot(a_m, Ptx_variable_APD[2,:],'-o', label = 'APD, 2 mrad') plot(a_m, Ptx_variable_PIN[2,:],'-*', label = 'PIN, 2 mrad') xlabel('Rx diameter (cm)'); ylabel('P_tx (dBm)') legend() grid() plt.show()

يمكن العثور على مقارنة مع حالة القناة الكهرومغناطيسية بين الأقمار الصناعية في مقالتنا في المجلة . كما يصف الأسباب التي دفعتنا في النهاية إلى رفض هذا السيناريو ، لكنني سأقول المزيد عن هذا هنا.

المزالق

وها نحن ، يتعرضون للضرب من الكتب المرجعية والصيغ الرياضية ، ولكن مع ذلك مستوحاة من النتائج التي تم الحصول عليها (نعم ما هو موجود - بحقيقة الرسوم البيانية الجميلة!) ، نحن نجري اجتماعًا نهائيًا قبل الدفاع. ونحن نواجه جولة جديدة من التفاصيل المهمة ...

تسوية رقم 2 : حسنًا ، حسنًا ، من الواضح أن هناك مكاسب. اقتنعوا أن هناك بالفعل نوع من قاعدة الأجهزة. ماذا عن الاستهداف؟ ربما سمعت عن نظام PAT ( P ointing ، A cquisition ، و T racking).

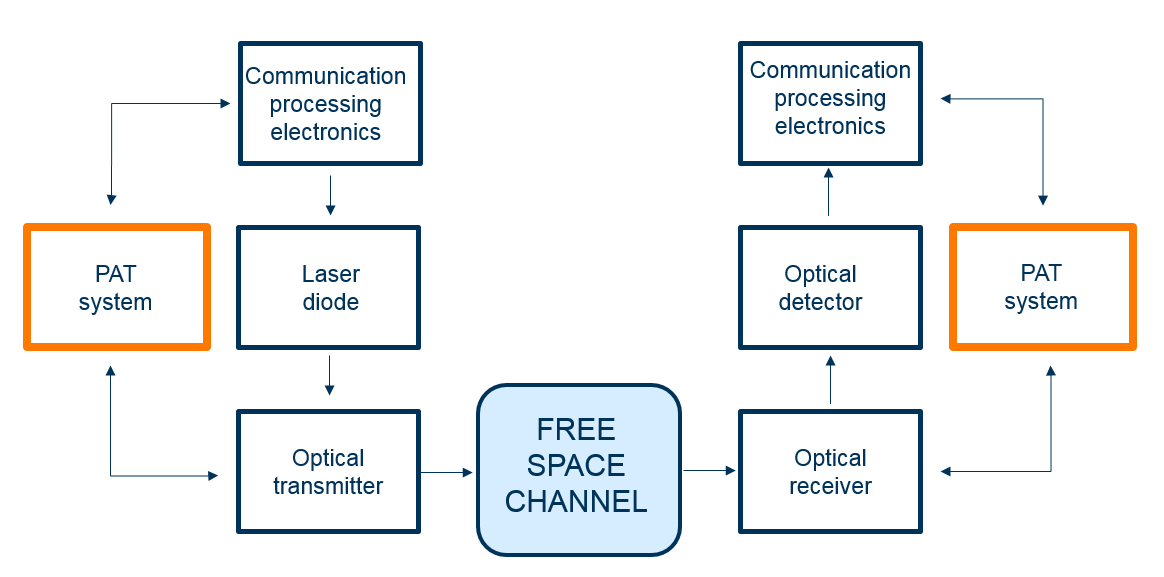
التين. 6. رسم تخطيطي مبسط لنظام الإرسال والاستقبال البصري اللاسلكي.

تسوية لا. 2 : نعم ، هناك أمثلة على القنوات البصرية للأقمار الصناعية الكبيرة [4] ، ومع ذلك ، في هذه الحالة ، يمكنك شراء قطر أكبر للمستقبل وزاوية انحراف ليزر أكبر وقدرة إرسال أعلى. علاوة على ذلك ، أعتقد أن CubeSat نفسها تهتز كثيرًا عندما تتحرك . بالنسبة لقناة إذاعية بترددات منخفضة نسبيًا ، قد لا يكون ذلك ضروريًا للبصريات - أنت تفهمها أنت بنفسك. هل هناك مثل هذا الاستقرار الدقيق ونظام PAT في الوقت الراهن؟

وكنا مدروس للغاية ...

تسوية رقم 2 : هذا ما ، من جهتي ، أعطيك تقييماً إيجابياً. ومع ذلك ، نصيحتي لك: النزول من السماء إلى الأرض ...

وقد استنفدنا ، استنفدنا: لقد قررنا عدم مواصلة المشروع باستخدام البصريات الساتلية. علاوة على ذلك ، حتى خلال اجتماعاتنا المتكررة ، جمعنا بعض الإرهاق ...

ومع ذلك ، لا ، لا ، وحتى ملاحظة أمل الطالب سوف تنزلق في قلب أن المعلم كان مخطئًا في شكوكه. لا ، لا ، وأريد أن أجد المفهوم ذاته في إنجازات التكنولوجيا الحديثة. وترتفع النظرة إلى الأعلى ...

أدب

Janson SW، Welle RP برنامج العرض التوضيحي للاتصال والاستشعار البصري التابع لناسا: تحديث // المؤتمر السنوي الثامن والعشرون AIAA / USU للأقمار الصناعية الصغيرة. - 2014. - S. 4-7.
Wolf، M.، & Kreß، D. (2003). الأشعة تحت الحمراء لاسلكية لنقل المدى القصير: رابط buoget مقارنة RF . الاتصالات اللاسلكية IEEE ، 10 (2) ، 8-14.
https://www.nii.ac.jp/qis/first-quantum/forStudents/lecture/pdf/noise/chapter12.pdf
Smutny B. وآخرون. 5.6 جيجا بت في الثانية وصلة الاتصالات بين الأقمار الصناعية // تقنيات الاتصال الحر بالليزر - الجمعية الدولية للبصريات والضوئيات ، 2009.- T. 7199. - S. 719906.

لكن ألا نلوح بالاتصال البصري؟ الليزر ، الفضاء ، CubeSat